基于Group Lasso的多重信号分类声源定位优化算法∗

吴江涛 胡定玉 方 宇 朱文发

(上海工程技术大学城市轨道交通学院 上海 201620)

0 引言

波束形成[1]是一种应用于信号波达方向(Direction of arrival,DOA)估计、声源定位的空间滤波处理方法，在汽车、航天、军事等领域都有着广泛应用，并在多声源定位领域得到发展[2]。目前已发展出多种波束形成算法，其中多重信号分类(Multiple signal classification, MUSIC)算法利用噪声子空间来最大化声源信号，较传统波束形成算法、Capon算法在抑制噪声能力、定位效果准确性上有明显优势。

MUSIC 算法最早由Schmidt[3]提出，并迅速在语音识别、三维声源定位等方向得到研究并应用[4−5]。以MUSIC 算法作为基础，加权MUSIC 算法[6]及改进MUSIC 算法[7−8]进一步提高了MUSIC 算法的准确性及适用性。为提高MUSIC 算法抗干扰能力，Gardner[9]将信号的循环平稳特性用于DOA估计，黄知涛等[10]利用信号的循环平稳特性提出了循环互相关MUSIC 算法，王超等[11]改进了预滤波MUSIC 算法，提高了目标声源分辨率。一系列的研究进一步提高了该算法的抗干扰能力及运算速度，但现有算法存在中低频段定位效果不准确及聚焦效果较差的问题。

针对MUSIC 算法在中低频段分辨率低及聚焦性能差这一缺点，本文提出基于Group Lasso[12]改进的MUSIC 算法，通过Group Lasso 算法增强MUSIC 算法声源定位聚焦效果。优化算法中，将MUSIC 算法计算结果作为Group Lasso 算法初始值，将导向矩阵与测量值作为Group Lasso 算法输入变量，通过组间L1 范数正则化，对扫描声源面信息进行稀疏筛选，且使用L2范数并加入阈值截断进行组内计算。通过仿真分析，证明基于Group Lasso的MUSIC 算法具有增强中低频段声源定位分辨率及聚焦性能的优势。

1 基于Group Lasso的MUSIC算法声源定位

1.1 MUSIC算法声源定位原理

MUSIC算法在波束形成算法基础上，将由测量信号得到的协方差矩阵分为信号子空间和噪声子空间，利用噪声子空间来最大化空间扫描声源面声源点输出值，获取高分辨率结果和优良聚焦性能[3]。MUSIC算法传声器阵列测量值Z表达式为

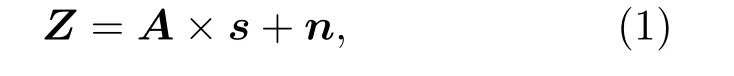
式(1)中，s为K ×1 维声源信号，K为声源数；n为M ×1 维噪声信号，Z是M ×1 维向量。A=[a1,a2,··· ,aK]为M ×K维导向矩阵[13]，其中a为导向向量，对于近场声源定位问题，采用球面波假设，其表达式为

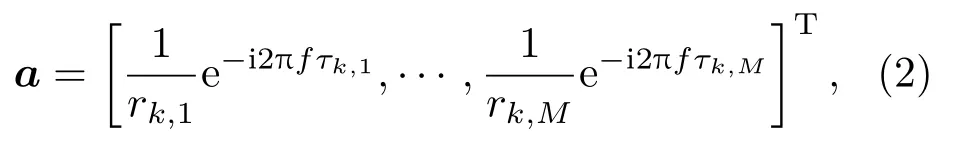
式(2)中，rk,m为第k个声源到第m个传声器的距离，τk,m为第k个声源到第m个传声器的声辐射传播时间，f为声源频率。MUSIC 算法原理是根据噪声子空间特征向量与导向矩阵列向量正交的关系来获取扫描点输出值，为得到噪声与信号子空间，首先得到协方差矩阵

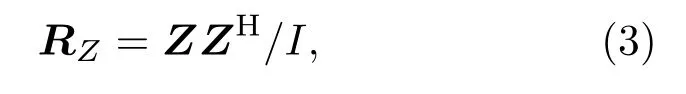
式(3)中，I为总的采样数，协方差矩阵RZ可分解为信号子空间RS和噪声子空间Rn，即RZ=RS+Rn。其中，RS=USΣSUHS，US表示信号子空间特征向量，ΣS表示信号子空间特征值；Rn=UnΣnUHn，Un表示噪声子空间特征向量，Σn表示噪声子空间特征值。对RZ进行特征值分解可得到

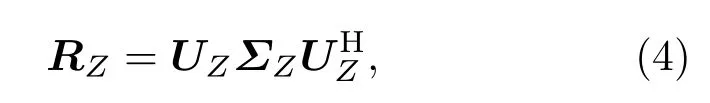
式(4)中，UZ为协方差矩阵特征向量，ΣZ=diag[λ1,··· ,λM]为对应于特征向量的特征值且特征值λ1> λ2>,··· ,> λM，特征向量正定(UZUHZ=UHZ UZ=IM)，IM为M维单位矩阵。

信号子空间的协方差矩阵为实对称阵，因特征值和特征向量的秩都为K(声源个数)，则信号子空间特征向量US和噪声子空间特征向量Un可表示为

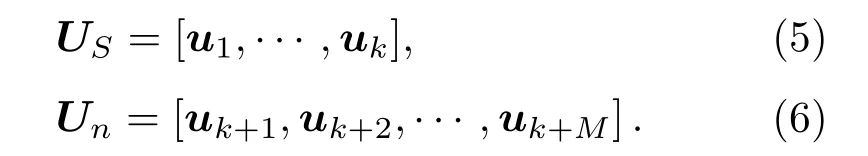
因为RZUn=ARSAHUn+σ2Un，σ2为噪声方差，且RZUn=σ2Un，可得到

式(7)中，RS满秩，非奇异，存在逆矩阵，因此当且仅当AHUn= 0 时，式(7)满足导向矩阵A中各列向量与噪声子空间正交的要求，UHn ak=0。当a为扫描声源面非声源点到传声器阵列的导向向量时，通过噪声子空间法得到MUSIC 算法在第k个扫描声源点处的声功率相对值

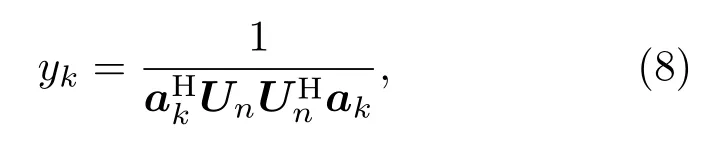
式(8)中，akei2πfrk/c为扫描声源到测量阵元面的导向向量，rk为扫描声源点k到传声器阵列的距离向量。当UHn ak= 0 时，MUSIC 算法在该扫描点输出值较大，反之输出值较小，MUSIC 算法最大化了声源点处的输出值，因此有较高的空间分辨率[13]。

1.2 基于Group Lasso的MUSIC算法

MUSIC 算法在高频声源定位分辨率及聚焦性较好，能够清晰地反映声源位置，但在中低频时出现分辨率低，聚焦性能差的缺点，无法满足应用要求。本文对其使用Group Lasso 算法进行优化，需要输入信息有待求量初始值y、测量值Z、导向矩阵A。Group Lasso 算法第一步需对y和A进行分组，即y= [yH1,yH2,··· ,yHN]H和A= [A1,A2,··· ,AN]。Group Lasso代价函数为

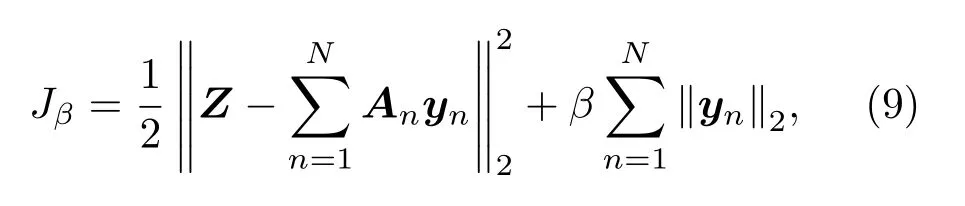
式(9)中，β为惩罚项的正则化系数，通过β来控制y的稀疏程度。

在Group Lasso 算法组间应用L1 范数正则化，导致在组水平上拥有稀疏性，此为提高MUSIC 算法中低频分辨率及聚焦程度的关键因素。在组内应用L2 范数正则化，使得组内数据平滑[14]。MUSIC算法声源定位在声源点位置扫描结果往往会有较突出的信号值，因此为了提高结果的分辨率及聚焦度，需要在组内循环中加入阈值，以截断MUSIC 算法中低频环境产生的虚影，该阈值通过动态范围给出，可保证信号位置信息不被破坏，且提高算法的分辨率及聚焦性能。

优化算法过程如下：

(1)定义组间迭代次数i，以式(8)中yk为初始优化目标。

(2)确定分组数，本文以扫描点数量为分组依据，设定组长度，n=1,2,··· ,N，n为分组数。

(3)在第n组计算时，首先确定本组残差值

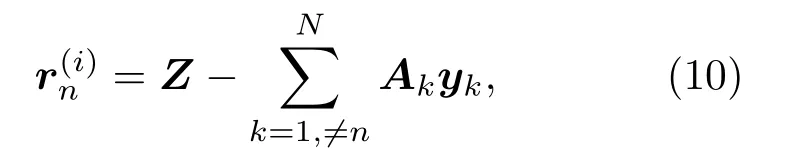
式(10)中，r(i)n为第n组残差值，Ak、yk分别为第n组的导向向量和MUSIC 算法输出值。并通过交叉验证确定β值，作为判断该组进行组内循环的依据。

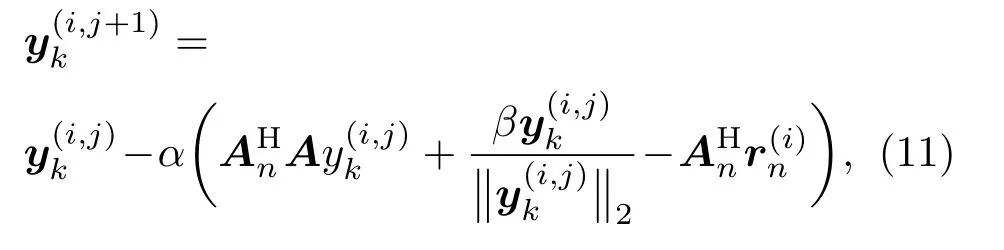
式(11)中，α为梯度值，当前后两次迭代误差小于10−3时停止第j次迭代，并使用动态范围计算阈值来截断输出值yk。动态范围pmax为初始输入值的最大值，本文pmin为初始输入值的最小值。选择0.1 倍的动态范围作为截断阈值Pc，即

当输出值小于Pc时输出为零，否则该输出值保持不变。

(5)组内循环结束，输出该组y(i)n值。

(6)重复步骤(3)∼(5)，当前后两次迭代误差小于10−3时停止第i次迭代，得到输出值y。

2 基于Group Lasso的MUSIC仿真

2.1 仿真设计

Group Lasso MUSIC 优化算法的目的是提高中低频环境下声源定位分辨率及聚焦性能，针对此目的设计仿真实验。第一，在低信噪比且信噪比恒定、扫描面位置与仿真声源面位置重合情况下，分别在单源和多源时分析Group Lasso MUSIC 算法在中低频对声源定位聚焦性能和分辨率的优化效果；第二，在低信噪比且信噪比恒定、声源为中低频环境下，改变扫描面到声源面的距离d，验证Group Lasso MUSIC 算法对声源定位聚焦性能的优化效果。

图1 随机传声器阵列阵元分布图Fig.1 Random microphone position map

仿真采用如图1所示的30 阵元随机传声器阵列，阵列半径为0.15 m。图2为仿真示意图，包括声源所在平面、扫描面、阵列面，其中，声源面到扫描面距离为d，声源面到阵列面距离为D=1 m不变。距离d是由于声源位置测量不准确导致的误差，在实际应用中，可能由于环境原因无法准确获取真实的距离D。

2.2 仿真分析

2.2.1 仿真1

设置声源为点声源，位于原点位置，信噪比为5 dB，声源面到扫描面距离d= 0，声源面到阵列面距离D= 1 m，分析在中低频声源情况下，Group Lasso MUSIC 算法的优化效果。单声源优化结果如图3所示，图3(a)、图3(c)、图3(e)分别为200 Hz、600 Hz、1000 Hz 时MUSIC 算法计算结果，从这三幅图中可看出，随着声源频率提高，声源位置的分辨程度逐渐提高，声源主瓣宽度逐渐缩小，聚焦性能呈增强趋势，但聚焦程度仍然低。

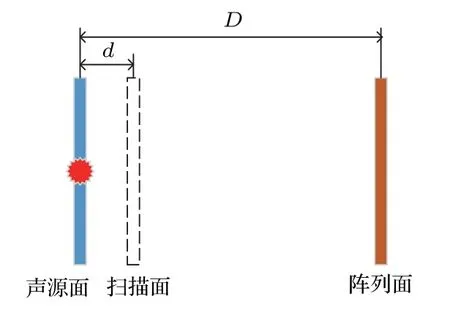
图2 仿真示意图Fig.2 Schematic diagram of simulation

图3(b)、图3(d)、图3(f)为基于Group Lasso 的MUSIC 算法优化结果，从这三幅图中可以看出，优化后的MUSIC算法声源定位效果受频率影响极小。Group Lasso MUSIC 算法经过对声源点稀疏筛选，聚焦性能较MUSIC算法有极大提高。

在单声源仿真基础上，将声源增加为双声源验证算法对多声源声场环境适应性及稳定性。图4(a)、图4(c)、图4(e)分别为双声源MUSIC 算法200 Hz、600 Hz、1000 Hz的计算结果，相较于单声源，双声源MUSIC算法结果分辨率要差。经Group Lasso算法优化后，如图4(b)、图4(d)、图4(f)，对于200 Hz仿真结果，稀疏程度并没有其他两者高，但主瓣宽度明显下降，分辨率显著提高。600 Hz 与1000 Hz 优化效果较好，分辨率提升明显，本文算法对中低频多声源环境有较好的适应性，效果稳定。

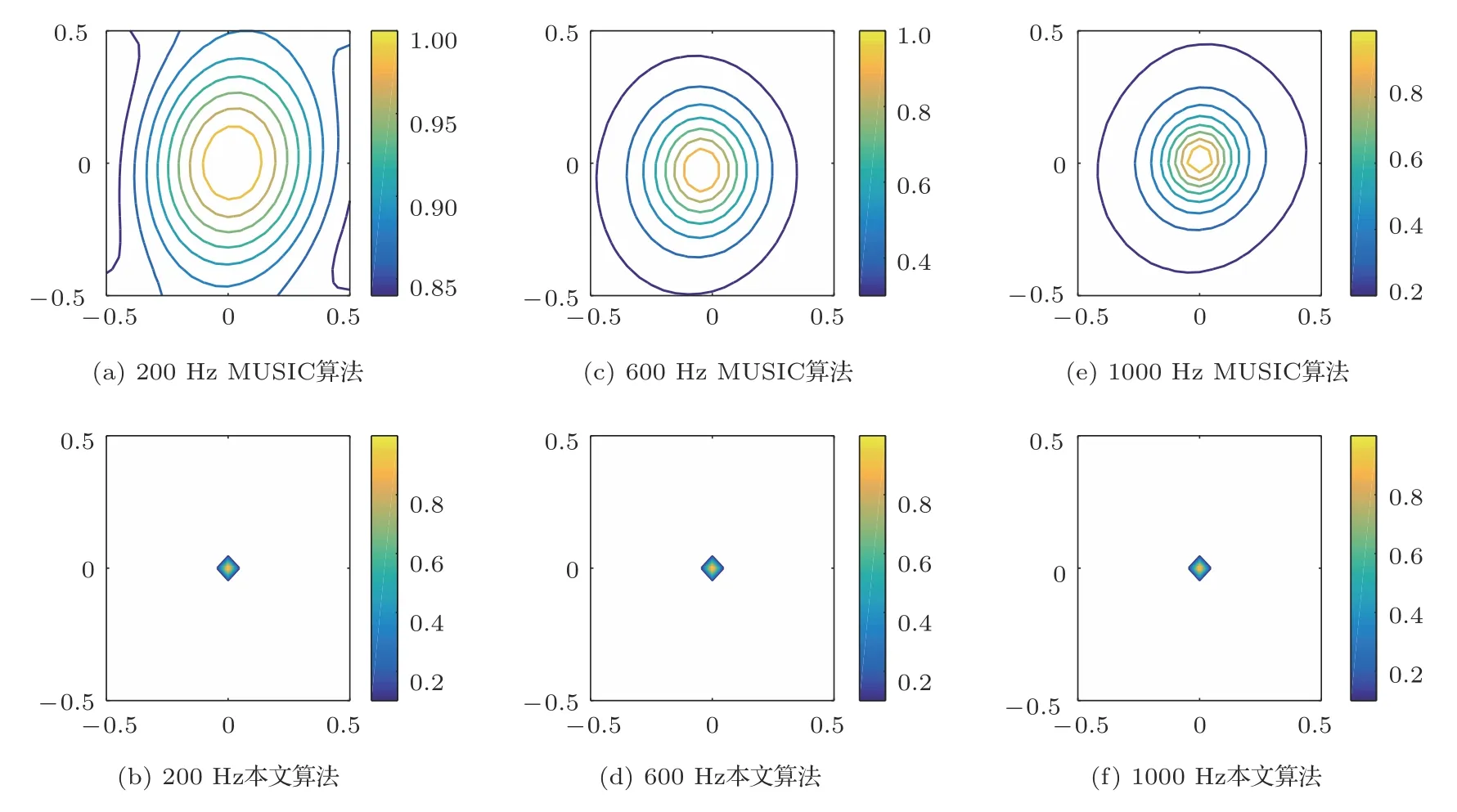
图3 仿真1 MUSIC 算法与本文算法效果对比图Fig.3 Comparison of MUSIC algorithm in simulation 1 and algorithm in this paper

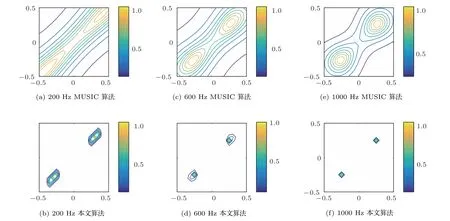
图4 仿真1 双声源MUSIC 算法与本文算法效果对比图Fig.4 Dual source comparison of MUSIC algorithm in simulation 1 and algorithm in this paper

2.2.2 仿真2

在仿真1 单声源参数保持不变情况下，分析1000 Hz 固定频率下、扫描面与声源面不重合(即)时Group Lasso MUSIC算法优化效果。在多数实际测量中，无法准确获取阵列面到声源面距离，因此会存在误差，本文中误差量为d。仿真2旨在说明随着误差d的变化，本文算法的稳定性。

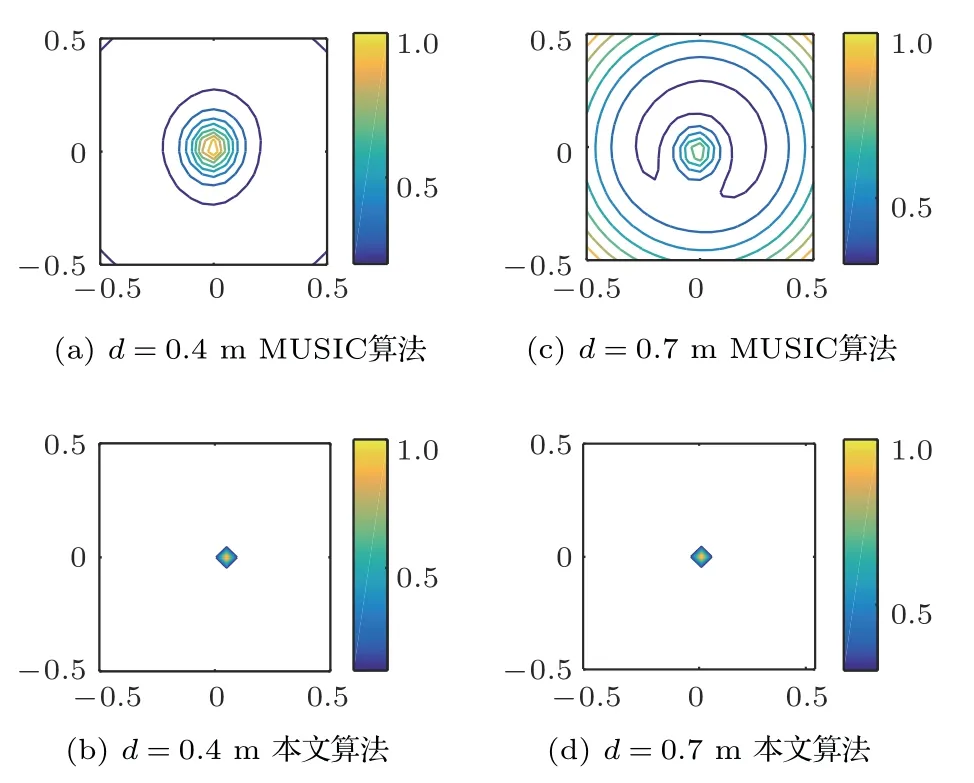
图5 仿真2 MUSIC 算法与本文算法效果对比图Fig.5 Comparison of MUSIC algorithm in simulation 2 and algorithm in this paper

如图5所示，图5(a)、图5(c)为MUSIC 算法声源定位效果图，图5(a)中，聚焦面边缘出现轻微虚影，说明在情况下，MUSIC 算法效果变差。图5(c)中，当d= 0.7 m 时虚影值已超过声源值，对声源位置的判断造成了严重干扰，分辨率及聚焦性能极差。经Group Lasso MUSIC 算法优化后，如图5(b)、图5(d)所示，算法有效地抑制了虚影产生，并提高了聚焦性能及分辨率。

3 结论

Group Lasso MUSIC算法将传统MUSIC算法计算结果作为初始值，通过Group Lasso 算法，经组间稀疏、组内截断等处理，改进了MUSIC 算法在中低频时，声源定位分辨率低、聚焦性能差的缺点。本文算法对于中低频环境单源和多源都有较好效果，对扫描面与声源面不重合时MUSIC 算法出现的计算失真情况得到了有效控制。在低信噪比环境下，本文算法能够对声源准确定位，稳定性与适应性较高。