基于IOE和SVM模型的府谷镇滑坡易发性分区

韩 玲, 张庭瑜, 张 恒

(长安大学 地球科学与资源学院, 国土资源部退化及未利用土地整治工程重点实验室,陕西省土地整治重点实验室, 西安 710064)

滑坡是一种时常发生的地质灾害，据报道2017年全国共发生7 122起地质灾害，造成372人死亡，25人失踪，173人受伤，直接经济损失约40亿元，其中滑坡灾害占全部地质灾害总数的75%[1]。陕西省府谷县府谷镇地处黄土高原北部，是西部大开发的重点地区。但府谷镇生态环境脆弱，水土流失严重，随着近年人口不断增长和工程活动的加剧，导致滑坡灾害频发，严重威胁人民群众的生命和财产安全。为了减少由滑坡所导致的人员伤亡和财产损失，对滑坡灾害的预测变的尤为重要。

滑坡易发性分区作为滑坡预测研究的第一步，目的就是要识别滑坡的高危险区域，减少滑坡预测的前期工作量。滑坡易发性分区图是滑坡易发性分区研究的最终成果，传统的分区方法不仅费时费力，所得到的结果也不够准确。统计分析模型因其计算较为简便、客观，分析结果易于解释，被成功用于大范围区域的滑坡灾害研究，如频率比模型(FR)[2-3]、确定性系数模型(CF)[4]、信息量模型(SI)[5-6]和熵权模型(IOE)[7-8]等。近年来，随着机器学习算法的兴起，为滑坡灾害的研究提供了新的思路。逻辑回归模型(LR)是根据现有数据对分类边界线建立回归公式，依次进行分类，模型实现简单，计算代价不高，速度较快，被广泛用于滑坡预测方面的研究[9]。人工神经网络模型(ANN)是利用训练样本来逐渐完善参数，通过大量引用中间层扑捉输入特征之间的关系，但它的准确率依赖于庞大的数据集[10]。支持向量机模型(SVM)是继人工神经网络之后的新一代智能算法，通过使用核函数将平面投射成曲面，提高泛化能力，在实际分类中展现出了很优秀的正确率，也被用于滑坡易发性分区研究[11-13]。统计分析模型和机器学习模型都有各自的优缺点，但在府谷镇区域还未曾出现基于这两类模型的滑坡预测研究。

为了有效预测滑坡易发的区域，客观对比统计分析模型和机器学习模型在滑坡预测中的效果，本文以陕西省府谷县府古镇为研究区，基于IOE模型和SVM模型开展府谷镇滑坡易发性分区研究，定量预测易发性区域，客观评价两种分类模型所得到的结果，为今后该区域的滑坡防治工作提供参考。

1 研究区概况及数据源

1.1 研究区概况

研究区位于内蒙古高原与陕北黄土高原东北部的接壤地带，总体向西倾斜的单斜构造之上，断裂、褶皱及次级节理裂隙构造较发育。地理坐标东经110°53′38″—110°06′32″，北纬38°59′42″—39°06′30″，新构造运动表现为震荡性上升，在地势上表现为西高东低，北高南低。据《陕西省区域地质志》[14]记载，近百年来研究区及附近未发生过地震烈度大于2.5度的地震，属无震害区，区域稳定性好，区内发育的地质灾害受内地质营力影响微弱。区内出露奥陶系、石炭系、二叠系、三叠系、侏罗系、新近系及第四系地层，岩层倾向南西—北西，倾角较缓，除黄河沿岸地层倾角达20°外，其余倾角5°～8°；气候类型属中温带干旱大陆性气候，黄河、孤山川河从境内流过，年平均降雨量420～460 mm，降雨主要集中在7—9月，且多以暴雨的形式出现，是研究区滑坡发育的主要影响因素；府店公路、神朔铁路、沿黄公路、府准公路等交通干线贯穿全镇，这些基础设施建设绝大多数要对山体坡脚进行开挖，形成高陡边坡，且保护措施又很差，加之区内人口分布密集，人类工程活动强烈，因此经常发生滑坡灾害。结合野外实地调查的结果发现研究区发育的滑坡灾害基本都属于降雨型滑坡，因此本文仅对降雨型滑坡的空间分布开展研究。

1.2 数据源

本文主要采用的数据源包括：(1) GF-1卫星影像(2017-08-31，轨道圈号23438)，用于提取NDVI、土地利用等参数；(2) 30 m分辨率数字高程模型(DEM)，主要用于提取坡向、坡度和高程等信息；(3) 1∶50 000地质图，用于提取岩土体类型和断层等信息；(4) 研究区气象水文资料，道路信息资料和野外调查资料等，用于提取道路、水系、降雨和滑坡等信息。

1.3 滑坡编录

确定研究区滑坡所在的具体位置以及其大小和形态是开展滑坡易发性分区的必备条件，而滑坡编录的目的就是要将这些滑坡数据整合在一起。通过野外实地调查，47个滑坡灾害中最小的滑坡面积约20 m2，最大的滑坡面积约13.5万m2，面积大于10 000 m2的滑坡数占总滑坡数的10%。因此，本文采用质心法将滑坡多边形转换成点要素制作滑坡编录图(图1)。将滑坡样本随机分成训练样本和测试样本两组，训练样本包含70%的滑坡点用于建立分区模型，测试样本为剩余30%的滑坡点用于验证分区结果的精度。

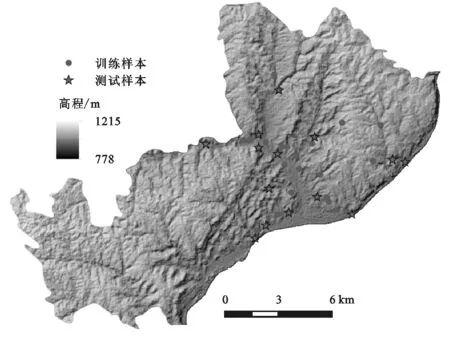
图1 府谷镇滑坡编录图

2 模型简介

2.1 熵权模型(IOE)

熵是对不确定性的一种度量，信息量越大，不确定性越小，反之亦然。根据熵的特性，可以通过计算熵值来判断一个事件的随机性及无序程度，也可以利用熵值来判断某指标的离散程度，指标的离散程度越大，该指标对综合评价的影响越大[15]。因此，在滑坡易发性分析中，可利用熵这个工具，计算出各个影响因子的熵权和综合评分，最终采用叠加的方式得到易发性分区[16]。具体计算方法如下：

(1)

(2)

式中：FRij代表滑坡发生的频率；Pij表示频率密度；a和b分别代表像元百分比和滑坡百分比。第j个因子的熵值可以表示为Hj：

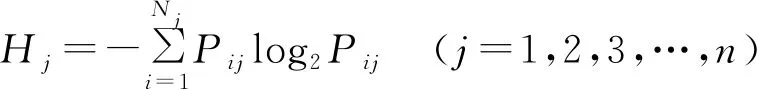
(3)

Himax=log2Nj

(4)

式中：Nj表示影响因子的分类数；Hjmax则是由Nj取对数得到，然后计算熵权值Ij：

(5)

Wj=Ij×FRij

(6)

最终得到每个影响因子的综合评分Wj。

2.2 支持向量机模型(SVM)

支持向量机(SVM)模型是基于核函数将线性不可分的数据转换为高维空间的线性可分的数据模式。一般SVM被设计成用于解决线性不可分和非线性不可分的分类问题，即同时存在正负样本，考虑一个训练样本集xi(i=1,2,…,n)由两类构成，表示为yi=±1。两类SVM的目标是寻求一个n维空间上的超平面，以最大间隔区分它们，同时使分开的两类数据点距离分类面最远，这个超平面既可以是平面也可以是曲面，数学上表述为：

(7)

约束条件为：

yi((w·xi)+b)≥1

(8)

式中：w2是超平面法向量的范数；b是标量；·代表标量乘积。引入拉格朗日乘数法则求极值，生成辅助函数如下(9)：

(9)

约束条件为：

(10)

对于一般的线性不可分实例，利用松弛因子εi(i=1,2,…,n)来调整约束条件得到(7) 的替代公式(11)：

(11)

这里v∈(0,1]是一个新引进的对于错误分类的罚值。另一方面，对于非线性不可分问题，通过引入核函数K(xi,xj)，使得高维特征空间中的内积运算可以通过原空间的一个核函数来隐含的进行运算[12]。本文采用目前被广泛认同的径向基核函数进行计算[17]。

径向基核函数：

(12)

2.3 影响因子分类

关于滑坡易发性影响因子如何选择至今还没有一个确切的定论[18]，因此本文依据前人的研究资料，结合野外调查选取坡度、坡向、高程、距断层的距离、距河流的距离、距道路的距离、岩性、土地利用、NDVI、降雨量共10种因素做为影响因子(表1)，其中岩性分类为A(粗砂砾石黄土状双层土体)、B(层状较软弱砂质碎屑岩)、C(层状坚硬—半坚硬砂泥岩互层碎屑岩)和D(层状坚硬碳酸盐岩)。应用ArcGIS 10.2和ENVI5.2软件，结合30 m分辨率的DEM数据和已有资料提取因子图层(附图18—19)。

4 结果与分析

4.1 基于IOE模型的滑坡易发性分区

在SPSS软件下计算每一类影响因子的熵权值和综合评分(表1)，将每一类影响因子对应的图层输入ArcGIS 10.2软件中建立IOE模型，计算滑坡易发性指数(Landslide susceptibility index，LSI)。最终LSIIOE的输出范围为0.069～1.544，利用自然间断点法将LSIIOE分为0.069～0.347，0.347～0.654，0.654～1.041，1.041～1.5444个区间，分别代表低易发区、中易发区、高易发区和极高易发区(附图20A)，各区所占的比例及对应的滑坡数量见表2。

4.2 基于SVM模型的滑坡易发性分区

利用MATLAB软件的SVM工具箱训练径向基核函数(Radial basis function)的SVM模型分类器，应用ENVI5.3软件对研究区进行像素计算。SVM模型输出结果范围为0～1，0表示灾害发生的概率为0%，1表示灾害发生的概率为100%，0.5代表灾害发生的概率为50%，是地质灾害发生与不发生的界限[19]。最终LSISVM的输出范围是0.140～0.861。将计算结果输入ArcGIS 10.2软件进行可视化，最后利用自然间断点法将LSISVM分为0.140～0.394，0.394～0.656，0.656～0.766，0.766～0.8614个区间，分别代表低易发区、中易发区、高易发区和极高易发区(附图20B)，各区所占的比例及对应的滑坡数量见表2。

表1 研究区影响因子分类和熵权计算

表2 4类易发区面积占比及对应的滑坡数量统计

4.2 精度检测和结果

本文应用ROC曲线分析的方法验证分区结果的准确度，其原理是通过改变诊断临界值，获得多对灵敏度与特异度值，绘制ROC曲线，计算比较ROC曲线下的面积，以此反映诊断试验的诊断价值。曲线下的面积(AUC)在0.50～0.70，说明有较低的准确性；AUC值在0.70～0.90，说明有较高的准确性；AUC值在0.90以上时说明有很高的准确性[20]。以灵敏度(Sensitivity)为纵坐标，以特异度(100-Specificity)为横坐标，将基于训练样本和测试样本的分区结果导入SPSS软件中分析，结果如图2所示。

从表2可以看出，基于IOE和SVM模型所得到的滑坡的敏感区(高易发区和极高易发区)所占比例大致相同，两种模型所到的敏感区空间分布十分相近。但是SVM模型所得到的敏感区范围(28.51%)比IOE模型(36.06%)更小，这表明SVM模型对研究区滑坡的发生更为敏感，同时也进一步缩小了滑坡定量预测的目标区域，可以有效提高今后研究区滑坡防治规划工作的效率。

根据图2可以看出，训练样本和测试样本的ROC曲线下的面积(AUC)均在0.70～0.90，说明本文所使用的两种分区模型在研究区进行滑坡易发性分区时，所得的结果的成功率和预测度在70%～90%，具有较高的精度。而在训练样本和测试样本的分区结果中，基于SVM模型所得到的分区结果的AUC值大于IOE模型。主要原因是SVM模型在高维空间中处理小数据集有极强的稳定性，但不太适合处理较大的数据集。核函数和其内部参数的选择对SVM模型的分类结果有着较大的影响，本文只选取了径向基核函数，建议后续研究增加核函数的种类做横向对比。

图2 训练样本和测试样本的ROC曲线

5 结 论

(1) IOE模型的分区结果中，极高易发区和高易发区占比为36.06%，对应的滑坡数量为42个；在SVM模型的分区结果中，极高易发区和高易发区占比为28.51%，对应的滑坡数量为46个。这与野外实际调查的结果相一致，也说明这两种模型分区结果的精度可以满足研究区滑坡防治的需求。

(2) IOE模型和SVM模型的AUC值均在0.70～0.90之间，表明这两种模型在研究区进行地质灾害易发性分区时具有较高的精度，可以为研究区滑坡预测提供参考。在测试样本的ROC曲线中，SVM模型的AUC值为0.859 4大于IOE模型的AUC值(0.833 7)，表明SVM模型更适合在研究区开展滑坡预测研究。