异形钢管混凝土构件受弯承载力计算
2019-05-22熊峰鄢凡饶玉龙肖家浩
熊峰,鄢凡,饶玉龙,肖家浩
(长江大学城市建设学院,湖北 荆州 434023)
异形钢管混凝土柱截面丰富多样、构造灵活、施工方便,可提高空间使用率,大大节省了成本并且该结构充分发挥钢管和混凝土的优点,具有优良的塑性和韧性,被广泛应用于大跨度及高耸结构[1,2]。国内外学者陆续对钢管混凝土承载力计算、力学性能和抗震性能等方面展开了研究。屠永清等[3]建立数值模型与既有试验结果进行对比,得出L形钢管混凝土柱轴压承载力计算公式。颜燕祥等[4]利用有限元程序提出3种截面钢管混凝土柱相关承载力计算方法。曹兵等[5]在试验及仿真软件计算的基础上,提出考虑轴压组合强度的L形钢管混凝土柱轴压承载力计算式。杜国锋等[6]通过轴压试验对比发现,异形截面(L形)钢管混凝土柱内置钢骨后承载力有所提高。雷敏等[7,8]研究了T形钢管混凝土柱的偏压及压弯性能,结果表明混凝土工作承担系数对轴力-弯矩曲线形状影响巨大。张继承等[9~12]通过试验研究发现,再生骨料取代率不是影响钢管混凝土柱力学性能及抗震性能的主要因素;通过拟静力试验及有限元模拟研究了T形柱-钢梁框架抗震性能,结果表明影响框架抗震性能的主要因素是轴压比。Ding等[13]通过改变箍筋配置情况研究方柱和矩形柱的滞回性能。
上述研究都局限于柱轴压承载力计算及性能研究,对受弯承载力的研究相较甚少,为此,笔者采用极限状态设计方法对异形钢管混凝土构件受弯承载力计算公式进行理论推导,并验证所推导公式的正确性,为受弯承载力计算提供了一种有效计算方法。
1 受弯承载力简化计算公式
采用极限状态设计方法推导L形和T形截面钢管混凝土构件受弯承载力简化公式,分析时,按文献[8]基本假定计算:①构件变形后符合平截面假定;②当构件最终发生破坏,认为此时拉、压区钢管均达到了屈服强度fy,而混凝土则达到了其抗压强度fc,不考虑受拉区混凝土的工作;③对受压区混凝土进行简化,其高度取按平截面假定所确定其高度为xc,相应的最大压应力则按混凝土轴心抗压强度fc计算。
1.1 L形钢管混凝土柱受弯承载力简化公式
由于L形截面钢管混凝土构件的特殊性,构件在2个方向上作用有弯矩荷载时,其受弯承载力的大小是不同的,因此当计算其承载力应对2个方向进行考虑。
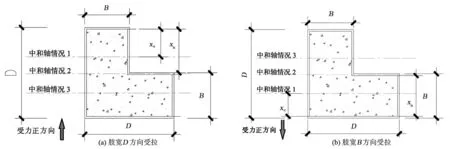
1)当肢长D方向受拉时,中和轴的位置可能会出现如图1(a)所示3种情况,则其受弯承载力:
情况1(xc≤xn):
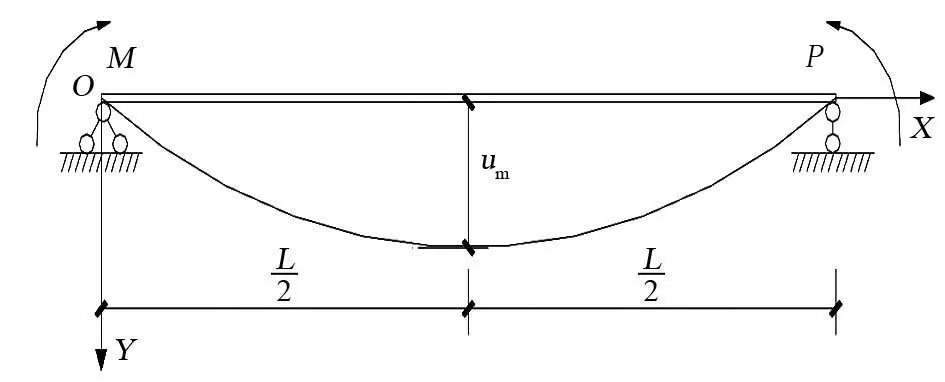
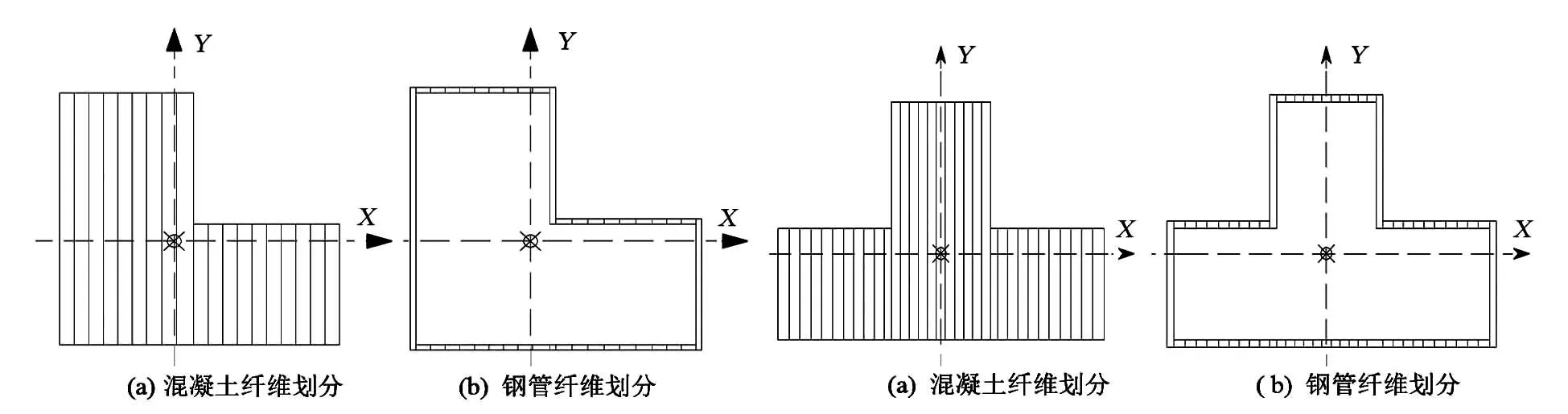
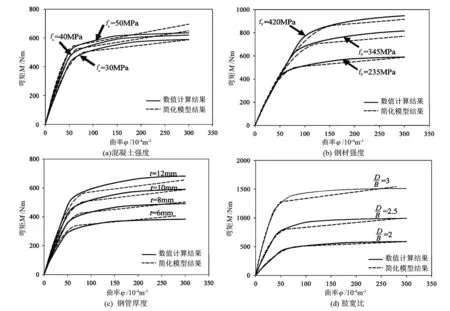
情况2(xn 情况3(xc>xn+t): 式中:t为钢管壁厚,mm;As为钢管面积mm2;B为肢宽,mm;D为肢长,mm;xn为中和轴到肢宽的距离,mm;Mu为受弯承载力,kN·m。 2)当肢宽B方向受拉时,中和轴的位置可能会出现如图1(b)所示3种情况,则其受弯承载力: 情况1(xc≤xn): D(D-t)]-fyt(D-B)2 情况2(xn (D-B)(D-1.5t-xc-|B-1.5t-xc|)tfy 情况3(xc>xn+t): 图1 L形钢管混凝土柱截面中和轴位置图 图2 T形钢管混凝土柱截面中和轴位置图 T形截面钢管混凝土构件的截面中和轴可能出现的情况共有5种,如图2所示。 对应图2所示截面中和轴情况,其受弯承载力简化公式如下: 情况1(xc≤C-t): (D-2t-xc)2+B(D-t)+ C(D-2xc-2t)] 情况2(C-t fytC(B+C-xc-1.5t+|C-0.5t-xc|) 情况3(C 情况4(C+B-2t 情况5(C+B-t 式中:C为腹板宽度,mm。 基于上述推导的受弯承载力计算公式,利用有限元软件Opensees建立纤维模型,通过参数计算得到弯矩-曲率曲线,从而验证模型的正确性。 图3 构件变形曲线 构件在受弯情况下的变形情况如图3所示,其中um为构件跨中挠度,L为构件的计算长度,M为杆端弯矩。由图3可知,构件两端为铰接,则构件在荷载作用下的挠曲线可以假定为正弦半波曲线,构件的挠度曲线方程可以表示为: 由此可确定构件跨中曲率为: 在计算前,先对构件截面中的核心混凝土和钢管进行截面纤维划分,具体划分如图4、图5所示。 图4 L形构件跨中零单元长度截面划分情况 图5 T形构件跨中零单元长度截面划分情况 设已知截面曲率φ,假设截面形心处的应变为ε0,以压为正。根据平截面假定,跨中截面上混凝土和钢管纤维单元第i单元形心处的应变值为: εci=ε0+φxci εsi=ε0+φxsi 式中:xci和xsi分别为第i个混凝土和钢单元在形心坐标轴中的坐标。 由材料的应力-应变关系,可得混凝土和钢材第i单元的应力: σci=fc(εci)σsi=fs(εsi) 式中:fc(εci)、fs(εsi)分别为混凝土和钢材的本构关系函数。 根据轴力的平衡条件可以得到: 由上式得到的第i单元轴力,Nin如果不等于零(即Nin≠0),说明力没有平衡,应调整假设的ε0,直到达到Nin=0,这时即可根据下式计算得到第i单元弯矩,Min为: 图6 L形钢管混凝土构件简化模型验证 图7 T形钢管混凝土构件简化模型验证 图8 异形钢管混凝土受弯构件典型的M-φ关系曲线 目前未见有关L(T)形钢管混凝土构件弯矩-曲率的试验报告,尚无法从试验角度来得到统一的构件弯矩-曲率的数学表达式。为得到L(T)形钢管混凝土构件的弯矩-曲率计算表达式,利用建立的纤维模型对L(T)形钢管混凝土构件的弯矩-曲率进行了全过程计算,受弯构件典型的M-φ关系曲线如图8所示,φe、Me和φ0、Mu分别为弹性阶段(OA)和弹塑性阶段(AB)结束时对应的曲率和弯矩。 1)L形钢管混凝土构件弯矩-曲率关系方程: 2)T形钢管混凝土构件弯矩-曲率关系方程: 1)采用极限状态设计方法推导了L形和T形截面钢管混凝土构件受弯承载力简化计算公式,为异形钢管混凝土构件受弯承载力计算提供了方法。 2)利用有限元软件Opensees进行大量参数计算,得到简化模型计算曲线及数值计算曲线,两者吻合较好,验证了模型的合理性。 3)采用经验证的简化模型进行参数计算得到了L形和T形钢管混凝土构件M-φ关系曲线的简化关系方程,为定义异形钢管混凝土柱塑性铰属性提供了有效方法。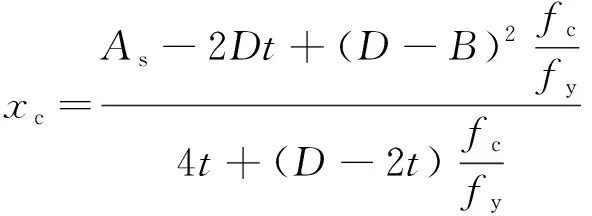
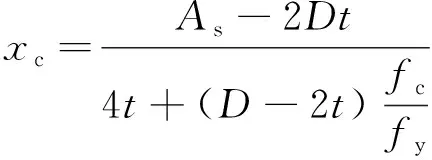


1.2 T形钢管混凝土柱受弯承载力简化公式
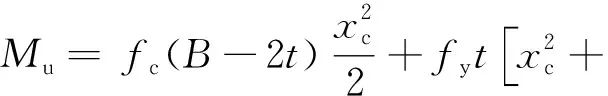

2 有限元分析
2.1 纤维模型
2.2 模型验证
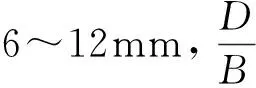
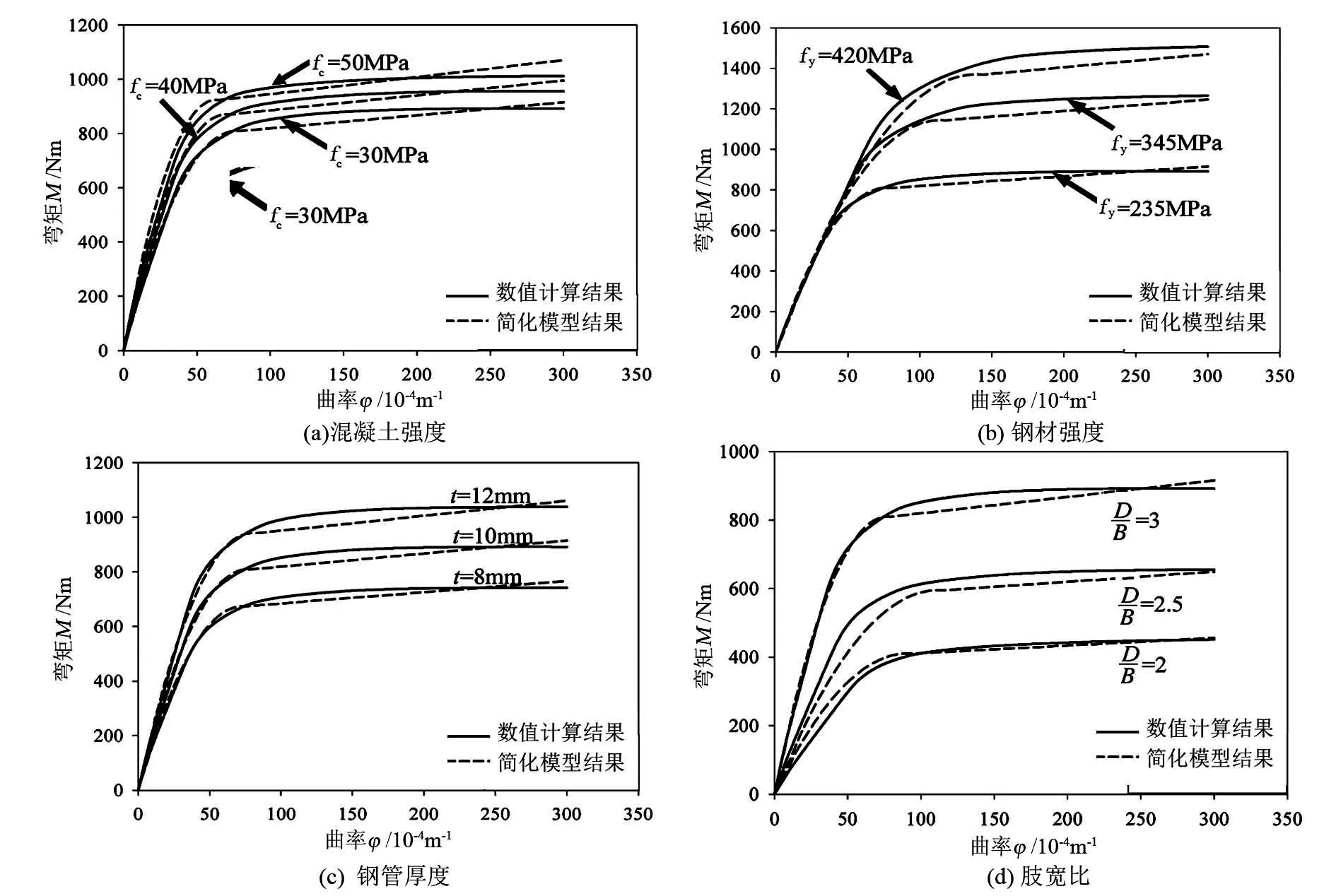

3 弯矩-曲率关系曲线方程
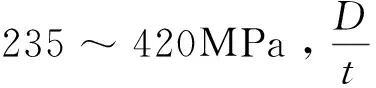
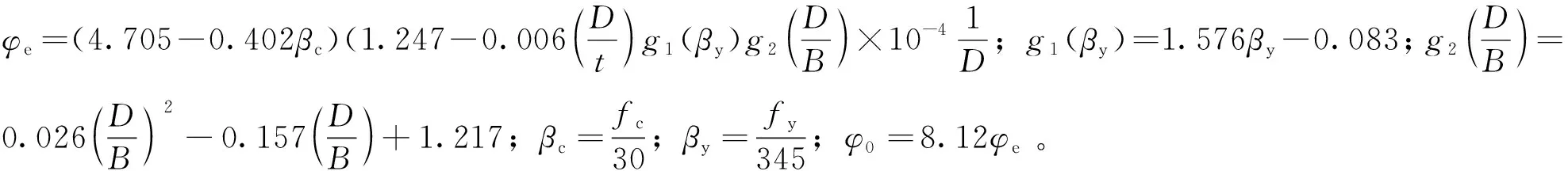
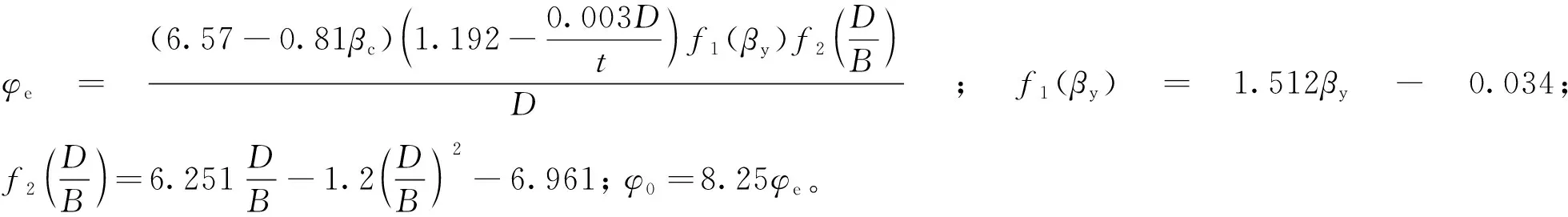
4 结论
