四川盆地东部下志留统龙马溪组页岩气藏应力敏感性及其对产能影响的定量评价

2019-05-22张国强

长江大学学报(自科版) 2019年4期

张国强

(中石化江汉石油工程有限公司井下测试公司，湖北武汉 430000)

近年来，页岩气藏开采发展十分迅速。作为决定页岩气产能的重要因素，页岩渗透率决定了页岩气在低渗储层中的流动方式。页岩渗透率具有明显的应力敏感性，在地应力场作用下，页岩渗透率展现出复杂的变化特征。水平井+水力压裂是页岩气储层的重要开采模式，该模式下，水力裂缝提供的高渗透率通道主导前期产能，基质渗透率主导后期产能。因此，明确页岩渗透率的应力敏感特性征对于定量评价页岩气产能具有重要意义。

张睿等[1]通过开展龙马溪组页岩岩心孔渗应力敏感测定试验，提出孔渗幂指数越大，渗透率应力敏感性越强。Dong等[2]通过物理试验建立了针对车笼埔断层页岩样本的孔隙度-渗透率模型，测试中通过改变围压获得样本渗透率应力敏感关系曲线，其研究认为增加应力导致的页岩渗透率损伤是部分不可逆的。姜宇玲等[3]采用脉冲衰减仪器测试龙马溪组页岩应力敏感性对渗透率的影响，避免了有效应力对初始渗透率的伤害造成的干扰，分析了围压和内压对渗透率测试的影响。此外，还可以通过建立模型的方法从理论上表征页岩渗透率的应力敏感性，该类模型通常考虑渗透率与围压变化的回归规律、孔隙压缩系数、等温吸附效应、气体扩散、孔隙弹性力学理论等[4～8]。Zhang等[9,10]从微观孔隙结构和弹性力学性质的角度出发，建立了针对页岩的应力-渗透率解析模型，指出页岩对有效应力的敏感性高于砂岩。

上述研究主要着眼于通过试验和理论方法确定围压变化与渗透率变化的关系，而较少对页岩渗透率应力敏感性与页岩气藏产能的关系展开研究。因此，笔者通过四川盆地东部下志留统龙马溪组页岩气藏应力敏感性试验获得渗透率变化规律，使用有限元方法建立流固耦合数值模型，定量评价应力敏感性对页岩气藏水平井开采模式产能的影响。

1 页岩样本应力敏感性试验

试验在常温常压下进行，使用氮气作为天然气的模拟气体。所用样本为取自四川盆地东部下志留统龙马溪组的页岩岩心。试验前，先将岩心在烘箱以70°C恒温加热50h制作成样本，测量其长度、直径及原始渗透率等基本参数，如表1所示。然后，使用“压差-流量法”进行气体单相渗流试验。试验的围压设备使用高精度多级柱塞驱替压力泵。试验中，将围压先加至4MPa，回压加至2MPa，保持注入压力为3MPa不变。再调整围压大小以改变有效应力，记录下围压增加过程中不同状态下对应的渗透率。当围压升至22MPa时，开始逐步降低围压并测定卸压过程中的渗透率变化情况。在围压的加压-卸压过程中，选取的围压节点分别为4、5、7、9、11、13、16、19、22MPa。

表1 页岩岩心样本基本参数

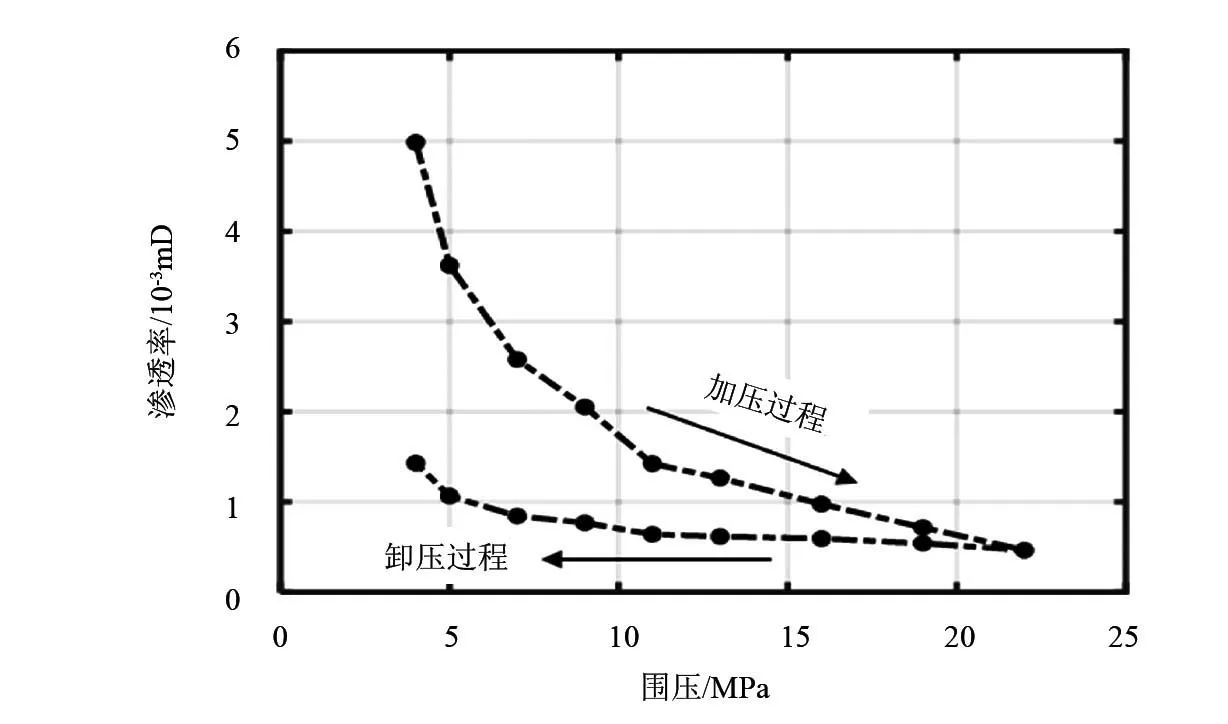
图1 页岩样本围压与渗透率变化关系曲线

根据上述试验步骤进行不同围压下的气测渗透率试验，所得结果如图1所示。从图1可以看出，加压过程中，渗透率有明显的下降，从最初4MPa围压时对应的0.005mD降至最高22MPa围压时的0.0005mD，渗透率降至了初始状态的10%，表现出了较强的应力敏感性特征。随后的卸压过程中，页岩样本渗透率由最低的0.0005mD恢复至4MPa围压时对应的0.0014mD，说明围压循环过程中的渗透率损伤是一个不可逆的过程：加压造成的渗透率下降不会因为卸压而完全恢复至初始状态。该试验中，卸压后渗透率(0.0014mD)仅恢复至初始状态(0.005mD)的28%，不可逆性较明显。该不可逆性是围压增加导致的孔隙喉道封堵造成的，孔隙喉道出现的封堵不会因为围压卸去而完全消除，因而造成永久性页岩渗透率损伤[4]。

2 应力敏感性流固耦合模型

2.1 流固耦合模型

流固耦合模型可以同时计算页岩储层中渗流场和地应力场的演化过程，而应力变化和渗透率演化分别是地应力场和渗流场的重要影响因素，因此，页岩流固耦合模型建模可以明确应力敏感性与页岩气藏产能之间的联系[11～13]。

采取全耦合方法建立流固耦合问题控制方程，并通过弹性模量拟合表示非线性弹性变形。

由达西定律得到渗流速度：

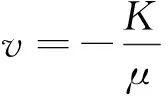
(1)

式中：v为气体渗流速度，m/s；K为页岩渗透率，mD；μ为流体黏度，Pa·s；▽p为压力梯度，Pa/m。

由质量守恒方程和流体扩散方程得到流动方程：

(2)

式中：ρ为流体密度，kg/m3；φ为孔隙度,%；b为比奥系数,1；Ks为固体体积模量，GPa；Mg为气体摩尔质量,g/mol；R为气体常数,J/(mol·K)；T为温度，K；Zg为压缩因子,1；p为孔隙压力，Pa;εv为体积应变，1；t为时间，s；▽(ρv)为流体流动的散度。

由固体力学应力平衡得到位移方程：

▽[σ-b(p-p0)I]=0

(3)

式中：▽为表示梯度的Nabla算子；σ为总应力二阶张量；p0为初始孔隙压力，Pa；I为单位矩阵。

式(3)表示全耦合形式下的渗流场与地应力场耦合，比奥系数b是Biot[14]提出的孔隙弹性力学理论中的重要概念，表示饱和流体孔隙介质发生固结作用时的压力和位移的关系。

试验时，气体流动会造成克林肯勃格效应，因此需要进行修正如下：

(4)

式中：Kg为试验测得渗透率,mD；bk为针对龙马溪页岩的修正参数[7],Pa；pavg为平均压力，Pa。

同时，渗透率也是孔隙度的函数，表示如下：

(5)

式中：γ为修正系数,1；K0为初始页岩渗透率,mD；φ0为初始页岩孔隙度,%。此处，初始代表样本开始测量时的状态。

之后，使用有限元方法和有限差分方法对公式进行离散，使用Newton法将非线性问题进行线性化，获得数值解。

2.2 应力敏感性修正

由试验数据可建立围压与渗透率的关系曲线，在耦合模型中，可以通过非线性弹性变形表征该关系。非线性弹性变形可表征非线性应力-应变关系， Scott[15]认为可以通过改变固体弹性模量的方法来表征该关系。因此，在加入应力敏感性修正项时，笔者使用了弹性模量E与围压σc的函数关系进行表征：

E=f(σc)

(6)

图2 弹性模量拟合结果

为了得到式(6)的具体形式，结合上述耦合模型，进行试验数据的拟合。拟合步骤如下：①初始设定一个弹性模量值，在一定的围压下代入耦合模型；②根据模型数值解得到平均渗透率；③如果该平均渗透率等于该围压下试验测得的渗透率，说明弹性模量设定值准确，否则，更改设定弹性模量值再次进行计算，直至模拟所得平均渗透率等于试验测得的值。需要注意的是，对于同一个围压值，围压状态可能是加压或者卸压，对应的渗透率不同，因此所拟合出的弹性模量也会不同。该过程所得弹性模量拟合结果如图2所示。

由图2可知，围压加压过程中，拟合得到的弹性模量持续增大。这是因为加压过程压实岩体导致弹性模量增大，应力-应变关系显示出非线性规律，在最大围压为22MPa时，对应最大弹性模量；在卸压过程中，由于压实作用减小，弹性模量也呈减小趋势；由于加围压导致的渗透率损伤是部分不可逆过程，加压和卸压阶段相同围压下根据渗透率拟合出的弹性模量不相同。卸压阶段拟合的弹性模量比加压阶段相同围压对应的拟合弹性模量小。图2中所示的拟合曲线可以用式(6)表达，将式(6)嵌入流固耦合模型中，即可得到该页岩样本考虑了非线性弹性变形的流固耦合模型。

3 产能影响定量评价

建立考虑非线性应力-应变关系的流固耦合数值模型后，通过算例计算定量分析应力敏感性影响下渗透率、应力和产能的关系。

3.1 岩心尺度模拟

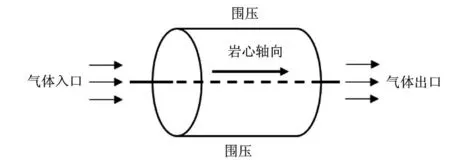
图3 岩心尺度下的三维圆柱体模拟模型

首先，建立岩心尺度的数值模型网格，针对围压循环过程进行数值模拟，表征岩心内相关变量的变化情况。根据表1岩心尺寸参数，建立如图3所示的三维圆柱体模型模拟流动和变形情况。初始时刻模型内孔隙压力等于入口压力，开始流动后模型内出现压力降。当气体流动达到稳定状态后，记录得到的数值模拟结果。

图4为加压状态下不同围压下沿岩心轴向方向的渗透率、渗透率空间导数、孔隙度、最小主应力数值模拟结果，加压状态下围压分别为5、9、13、19MPa。轴向位置为0时代表岩心入口处，为3.94cm时代表出口处。

图4 加压状态下不同围压下渗透率、渗透率空间导数、孔隙度和最小主应力沿岩心轴向分布模拟结果

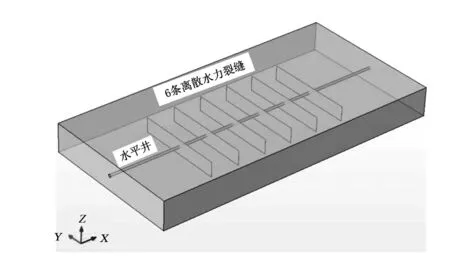
图5 页岩气藏水平井产能评价模型

由图4可知，渗透率沿轴向减小，与孔隙压力分布梯度相关。同时，围压增大造成渗透率快速下降。孔隙压力梯度也使孔隙度沿轴向减小，围压增大也造成孔隙度减小。式(5)可以解释图4中渗透率和孔隙度的相似空间分布趋势。最小主应力沿轴向增大，且随围压增加而增加。围压增加说明压实作用变强，对应着主应力增加；与初始状态相比，孔隙压力的变化越靠近出口处越大，导致有效应力沿轴向升高，造成最小主应力沿轴向增大。

3.2 应力敏感性对产能的影响

为了评价应力敏感性对页岩气藏水平井产能的影响，笔者建立了水平井尺度数值模型，以模拟不同应力条件下页岩气藏水平井产能的变化情况。图5是页岩气藏水平井产能评价模型，该模型中包括1口水平井和6条离散水力裂缝。模型具体参数见表2。模拟时采用弹性模量和应力的函数关系表示应力敏感性。

表2 产能评价模型参数

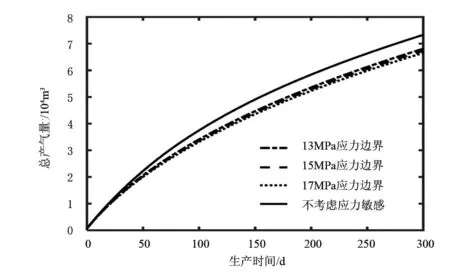
图6 不同应力状态对总产气量的影响

使用该模型模拟4种不同应力状态下的产能情况，结果如图6所示。不考虑应力敏感性的情况下,渗透率未受到损伤，因此总产能最高。考虑应力敏感性时，由于出现弹性模量变化和渗透率变化，对应产能也出现变化。不考虑应力敏感性时300d内总产气量为7.33×104m3；应力为13MPa时总产气量为6.81×104m3，相比不考虑应力敏感性下降7.09%；应力为15MPa时总产气量为6.73×104m3，相比不考虑应力敏感性下降8.17%；应力为17MPa时总产气量为6.65×104m3，相比不考虑应力敏感性下降9.24%。