黄沙百战穿金甲：浅谈穷举法

孙毅坚

孙子在兵法中强调，战争的目的是为了胜利而非杀戮的快感，同样，数学的学习是为了更快更精准地解题，而非仅仅用来炫技.有时候，解决一道难题的最佳方案，也许反而是最纯粹的列举.希望这篇文章能引起各位的注意，毕竟数学能力的强弱更主要是在于分析和解决问题的能力，而非知识量的多少.

例一列数：1，2，3，5，8，13，…请问第1993个数被6除余几？

这道看似是名校自主招生的题，实际上来自一本小学四年级的奥数讲义书.显然，所谓“一列数”即去掉首项1的斐波那契数列（斐波那契数列：1，1，2，3，5，8，…），对这样庞大的数字求解，其背后一定有规律存在，于是我随手便列举了7位：

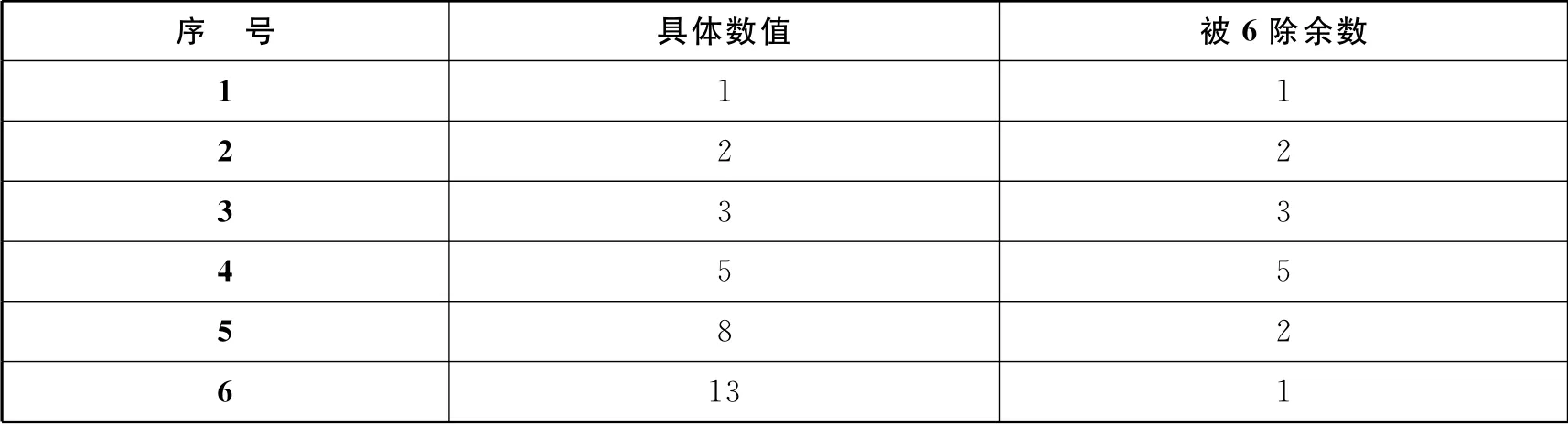
表1

随着数列的展开，具体数值将滚雪球般越来越大，这时依然靠它求被6除的余数显然不够理智，观察可以发现，最右边由被6除余数组成的新数列之间，也存在着类似斐波那契数列的性质，简单证明一下：

设一列数为{an}，一列数被6除余数为{bn}，

再设an=6T+p，an+1=6T+q，T ∈N，p，q∈{0，1，2，3，4，5}，

则bn=p，bn+1=q，an+2=12T+p+q.

因为p+q＜12，

那么借助{bn}的性质可以免去计算具体数值，这样列到16位：

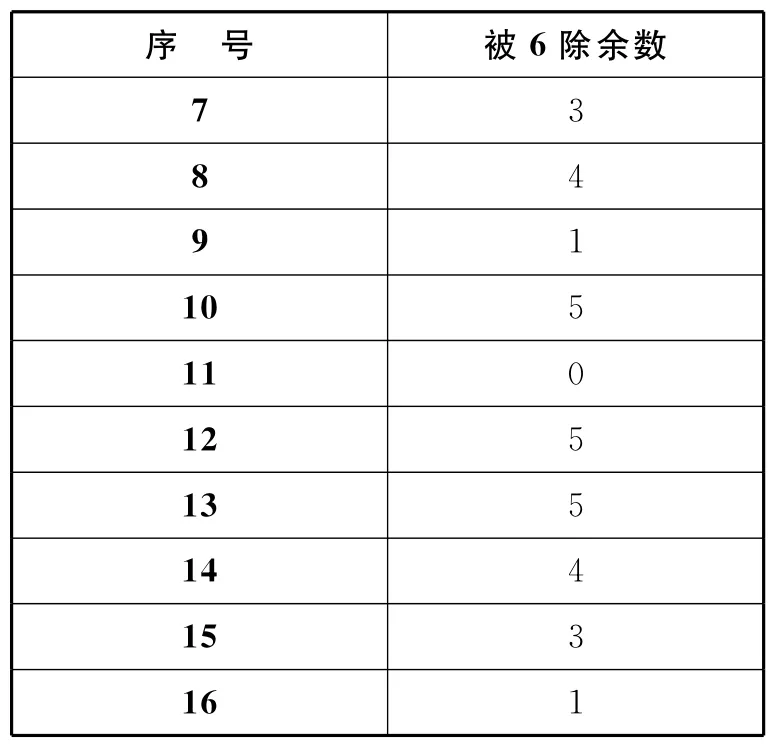
表2

至此，再回头看产生的新数列，可以说还是没有头绪.我不禁失去了耐心，将题目上传到了一个数学爱好者讨论群中，很快，各种学霸和数学竞赛牛人都各抒己见，我则继续默默列举.

有人搬出了特征方程，将数列通项解出：

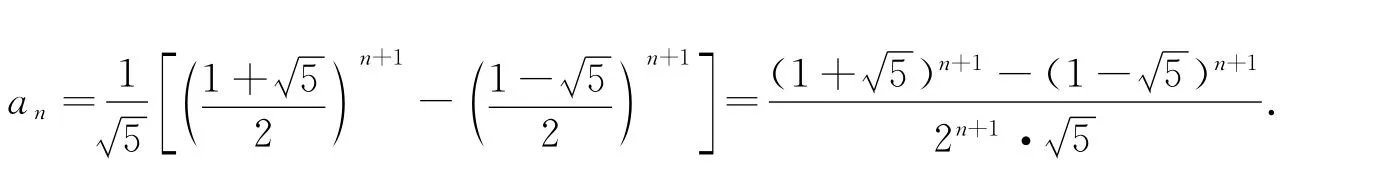
可是谈及被6除余几却依然无人作答，这时，我惊喜地发现，列举有了突破性进展.

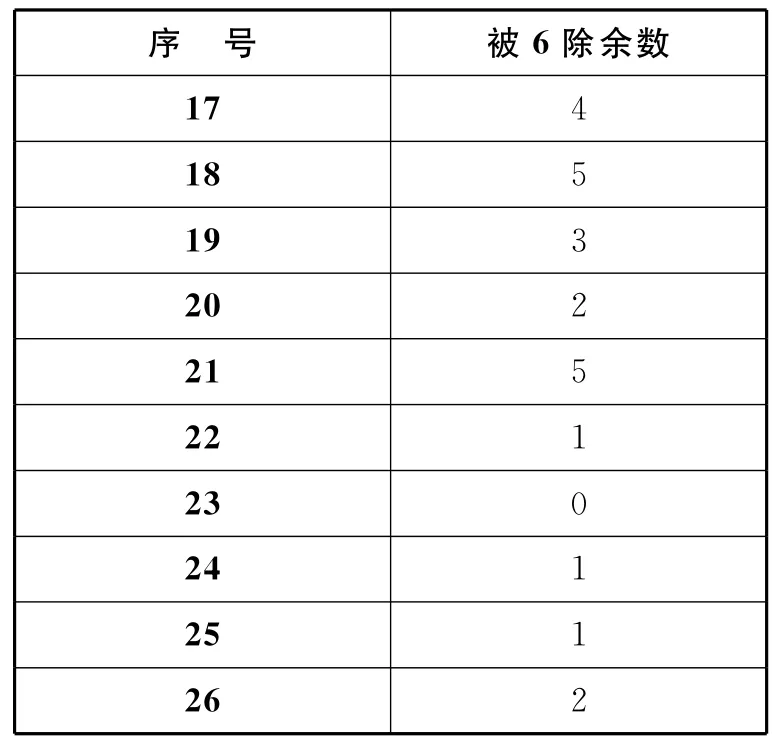
表3

山重水复疑无路，柳暗花明又一村.如表3所示，乱序的数字在第24位出现了转机，即第24位不仅回到了第1位的数值1，其前一位为0，那么第25位为1、第26位为2、……分别对应第1、2……位.所以说，这个“一列数”呈现出以24为周期的循环.这时经简单运算，答案为1.为了保险起见，我又在网上找到了原题与详解，答案正确并且穷举为目前我能查到的唯一方法，解析最后一句“本题旨在考验学生的意志力与科学精神”，仿佛是对我默默穷举，耐心求解的一种称赞.

我上传答案后，仍有人不死心，誓要熬夜思考其他方法……祝他成功.而整理草稿的我不禁想起一句话，可能与文题不太吻合：“有时我们走得太远，以至于忘了为何出发.”

解完了这道工程量颇为浩大的题，我总结归纳了一下，得到有关穷举法的几个要点：

①题干中出现几百几千这样极大的数据时，往往会有规律可循，可先通过穷举发现规律，再进行代数证明；

②在穷举过程中，尽量避免计算过于庞大的数据，而是在数值比较小的数据中找规律.这需要在解题过程中随时化繁为简；

③面对较难的，求具体数值、最值的相关问题时，穷举往往是最先与最后要考虑的方法，先小规律地列表，未果后考虑其他思路，若依旧毫无成效，则可放大穷举的范围，对填空题而言，这种相对客观的解题策略与方法既省时又高效；

④穷举并非单纯的全部列举，在适当的条件下结合两分法等，在对过程的分析中可以跳过一些无意义的列举，抓住性质缩小范围，寻找列举中的“转机”.

那么，让我们回到高中数学中来，尝试解答这道2018年高考江苏卷的填空压轴题：

已知集合A={x|x=2n-1，n∈N*}，B={x|x=2n，n∈N*}，将A∪B的所有元素从小到大依次排列构成一个数列{an}，记Sn为{an}的前n项和，则使得Sn＞12an+1成立的n 的最小值为_________.

这是绝大多数资料上提供的解答方法，很“江苏”：

设An=2n-1，Bn=2n，n∈N*，则当Ak＜Bl＜Ak+1（k，l∈N*）时，

2k-1＜2l＜2k+1，有则k=2l-1.

设Tl=A1+A2+…+A2l-1+B1+B2+…+Bl，则共有k+l=2l-1+l个数，即Tl=S2l-1+l，而A1+A2+…+A2l-1=

B1+B2+…+Bl=则Tl=22l-2+2l+1-2，

则l，Tl，n，an+1的对应关系为：

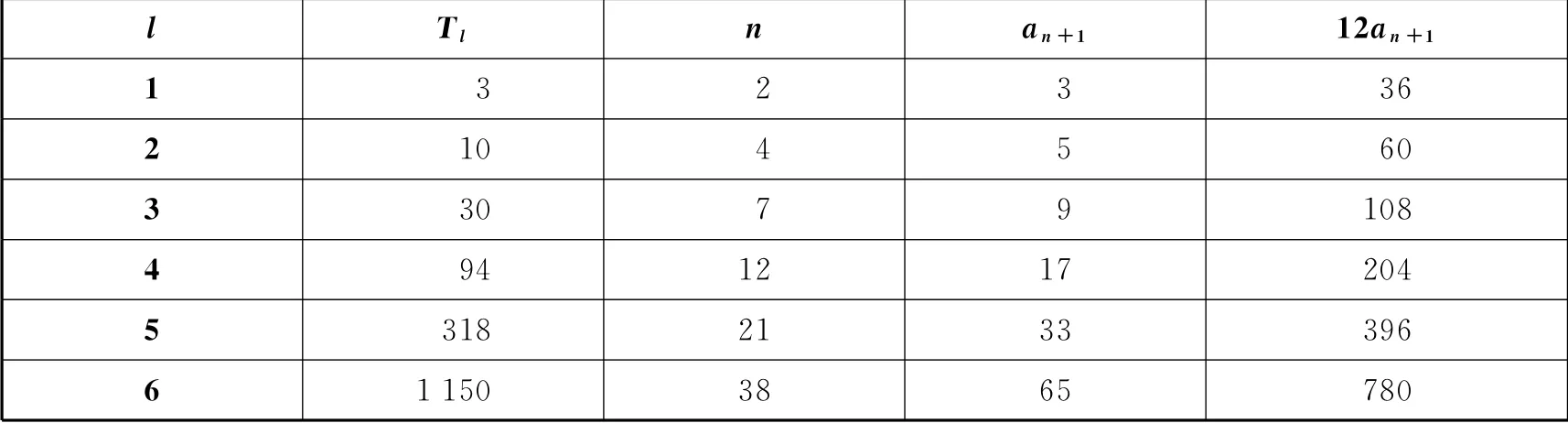
表4

观察到l=5时，Tl=S21＜12a22，而l=6时，Tl=S38＞12a39，则在n∈（21，38），n∈N*时，存在n使得Sn＞12an+1，此时T5=A1+A2+…+A16+B1+B2+B3+B4+B5，则当n∈（21，38），n∈N*时，

an+1=An+1-5=An-4，12an+1=12［2（n-4）-1］=24n-108，

Sn-12an+1=n2-34n+195=（n-17）2-94，

则n≥27时，Sn-12an+1＞0，即nmin=27.

不过，用穷举法可能还要更简便一点：

{an｝显然，2n与2n-1的增幅差距很大，将Sn拆开运算的压力不大，所以我先选取了n=11（因为在历年高考压轴题中11这个答案出现频率比较大），

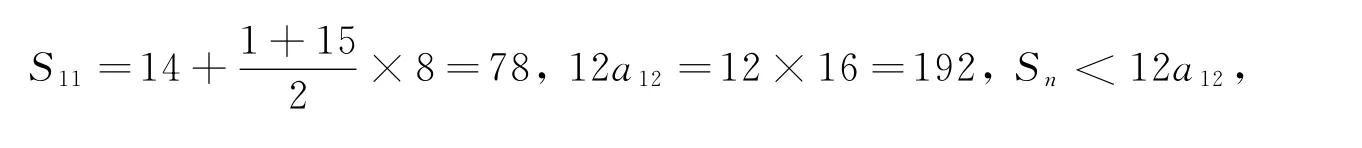
未果，接着选取n=21和n=31，

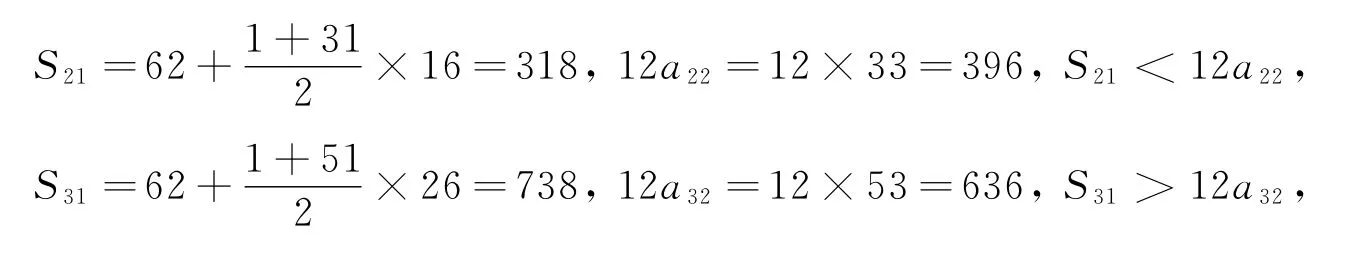
曙光就此出现，立即两分法处理，

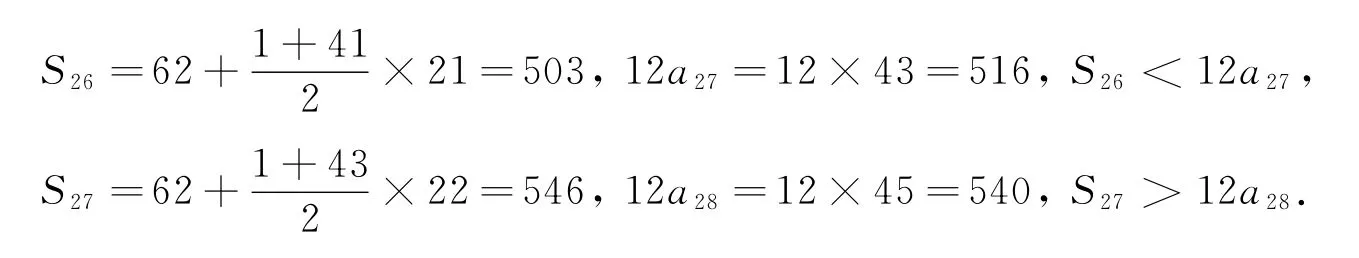
得到答案为27，对于计算能力可观的学生来讲，穷举似乎比需要讨论的函数法更加迅猛，虽然不少行为更多是出于“下意识”，但在并不严谨的解题过程结束后可以再回头思考原理，万变不离其宗，就算没能直接算出结果，列举的过程中想必也能帮助考生更准确地把握函数表达式.

没有花哨的公式，思考加上5次基本运算，一道高考压轴题和小学生的思考题一样烟消云散.下一次遇到符号字母们解决不了的问题，不要太狂躁，不如先列几个数看看，回到原点，万一那就是终点呢？

老师点评：孙毅坚同学爱好学习，善于思考，而且有坚韧的毅力.对于穷举法，许多孩子是没有耐心去尝试的.正如试题解析所言“本题旨在考验学生的意志力与科学精神”，学生的意志力与科学精神是可以通过考试的形式得到考查的.四年级的奥数题对于一个高中生来说应该是不算太难.但是方法的选择显得很重要，本题如果不用枚举法去解，则要费时费力得多，2018年江苏高考题也是这个道理.枚举法是最基本且重要的方法，学生要有耐心去尝试.当然并不是要求没有目的地做，而是要求学生能够边做，边观察，边思考，这样才能找出规律，从而使问题得到解决.久而久之，学生的数学抽象、直观想象、逻辑推理、数学运算等数学核心素养就能够得到培养.