一种新型液压阀用电磁驱动机构的设计与研究

杨智超， 邓 斌

(西南交通大学先进驱动节能技术教育部工程研究中心， 四川成都 610031)

引言

液压换向阀在开启和换向时往往会产生较大的冲击和震荡，这种冲击严重时会使液压管子爆裂，损坏密封装置和液压仪表，并会产生很大的噪声，给系统的正常工作带来隐患。目前降低液压冲击的方法主要有：降低换向阀的换向速度，增大管径；设置缓冲装置；通过电气控制方式缓冲液压冲击。但是这些方法并不能彻底解决液压冲击带来的危害， 而且还可能会降低液压系统的响应速度[1-3]。本研究从改造液压元件的驱动方式出发，设计了一种能够降低、调节液压阀换向冲击的新型阀用电磁驱动机构。

该新型阀用电磁驱动机构主要由双稳态永磁操动机构、隔磁铜片和MRD三部分组成，双稳态永磁操动机构的驱动杆和MRD的活塞杆做成一体式的，双稳态永磁操动机构与MRD之间安装有铜片，这样能防止双稳态永磁操动机构中的磁场对MRD中的磁流变液(MRF)性能的影响。其中MRD由端盖、缸体、线圈、活塞、驱动杆等组成，在缸体内部充盈着磁流变液；双稳态永磁操动机构由上端盖、上线圈、永磁体、下线圈、动铁心、机体以及下端盖组成，图1所示是该新型阀用电磁驱动机构的示意图。

1．MRD 2.隔磁铜片 3.双稳态永磁操动机构 4.端盖 5.缸体 6.线圈 7.活塞 8.磁流变液(MRF) 9.驱动杆 10.上端盖 11.上线圈 12.永磁体 13.下线圈 14.动铁心 15.机体 16.下端盖图1 机构简图

双稳态永磁操动机构的作用是在保持位或换向过程中代替传统的电磁线圈使阀体处于保持位或实现换向，磁流变液阻尼器(MRD)的作用是换向时通过控制输入电流的大小，来改变MRF的屈服强度，可以根据使用需求输出可控阻尼力来调节液压阀的换向电磁驱动力进而降低液压阀换向所带来的冲击力。该新型驱动机构由于采用双稳态永磁操动机构实现换向及保持工作位，因此具有节能环保、可靠性高等优点，而MRD由于其阻尼力具有连续可调，可重复利用的优点，使该新型阀用电磁驱动机构具有工作稳定性高，能最大限度降低液压冲击、保证液压系统持续正常工作的功能，图2所示是该机构操作过程示意图。

1 双稳态永磁操动机构的设计与仿真

1.1 双稳态永磁操动机构的设计

双稳态永磁操动机构采用圆柱形结构，主要由永磁体、动铁芯、上线圈、下线圈以及机体等组成，永磁体的作用是在由它和动铁心、机体以及气隙共同组成磁路里，按照磁阻最小原则产生一个恒定的磁场，依靠永磁体的磁力使动铁心和驱动杆保持静止，需要换向时，电磁线圈通电产生换向电磁力与永磁体的电磁力作用产生合力，驱动动铁心和驱动杆完成换向[4]。

图2 机构操作过程示意图

根据电磁阀工况要求，双稳态操动机构的设计参数如下：

永磁体产生的稳态保持力：F0≥90 N

电磁线圈产生的换向力：F1≥110 N

行程：s=4 mm

为简化分析过程，在设计计算及仿真分析过程中，假设材料均具有各向同性，忽略线圈温升对导磁材料磁阻及线圈磁势产生的影响，不考虑导磁材料的磁滞效应，不考虑涡流损耗对永磁体性能的影响[5]。

综合考虑永磁材料的性能特点及设计要求，永磁体采用环形结构，永磁体材料选用NdFeB 400/107，其主要性能参数如下：

剩磁Br≥1.41 T

最大磁能积(BH)max=374～406 kJ/m3

矫顽力Hcb≥938 kA/m

内禀矫顽力Hcj≥1075 kA/m

动铁心及机体在机构中作为传递和转换磁场能量的部件，需要具有较高的磁导率，较低的矫顽力，选用电工纯铁DT4，它具有饱和磁感应高的特点(293 K达21580 Gs)，其具体参数如下：

矫顽力Hcb≤96 A/m

最大磁导率μm≥0.0075 H/m

驱动杆采用铜制造，其导磁性能较差，在设计计算中可作为非导磁材料处理。

由于机体的材料采用电工纯铁，因此双稳态永磁操动机构设计成圆形形状，采用经验公式法计算[6-7]，机构各主要部件具体参数如下：

永磁体：内径：17 mm，外径：29 mm，高度：3 mm

动铁心：内径：8 mm，外径：15 mm，高度：38.8 mm

机体：内径：59 mm，外径：64 mm，高度：43 mm

驱动杆：直径8 mm

线圈：内径：17 mm，外径：57 mm，匝数：1000匝，换向时通入电流：1.5 A

1.2 静态、瞬态磁场特性有限元仿真分析

液压阀在保持位时，双稳态永磁操动机构依靠永磁体产生的电磁力实现阀体稳定在保持位；液压阀换向时，需要对双稳态永磁操动机构的保持位相对方向的线圈通入电流，大小为1.5 A，使线圈产生的电磁力能够克服永磁体的电磁力实现换向。结合双稳态永磁操动机构的设计尺寸，利用Maxwell软件分别对其进行静态(电磁线圈未通电的状态)、瞬态(电磁线圈通1.5 A的电流时的状态)磁场有限元分析。由于双稳态永磁操动机构是轴对称的，因此为了节省计算时间，在Maxwell软件建模时采用关于z轴的轴对称模型[8]。

双稳态永磁操动机构Maxwell电磁场有限元分析步骤：

(1) 前处理：建立关于z轴对称的模型，配置各部件材料属性，划分网格，施加边界条件，将驱动杆及动铁心设置为运动部件，并为运动部件设置运动参数、添加力学载荷[9-10]，给线圈设置电流源激励；

(2) 求解；

(3) 后处理：查看动铁心及驱动杆运动过程中的受力变化情况。

如图3所示仿真得到在双稳态永磁操动机构的运动部件所受磁场力随时间变化的曲线，该曲线表明动铁心在0时，运动部件受到永磁体与电磁线圈的电磁场合力，大小为F2=22.2575 N，方向指向z轴正方向，两力的合力驱动双稳态永磁机构实现换向；随着时间的增加，动铁心及驱动杆所受磁场力不断增大，位置也不断增大，这表明机构能够连续的运动到行程末端，在换向完成即5 ms时，运动部件所受合力大小达到F3为280.9853 N，方向为z轴正方向。

图3 瞬态磁场下双稳态永磁操动机构运动部件受力变化曲线

2 MRD的设计与仿真

2.1 各部件结构设计及材料选择

假设双稳态永磁操动机构的电磁线圈在其运动部件运动完行程全程的时间内始终通电，由于MRD的作用是产生阻尼力以降低双稳态永磁驱动机构的换向末端所带来的较大冲击力，为了避免出现MRD所产生的阻尼力大于双稳态永磁操动机构的电磁驱动力，使双稳态永磁操动机构不能实现换向的现象出现，因此对MRD提出如下要求：

(1) 为使双稳态永磁操动机构即使受到MRD的最小阻尼力时依然能够驱动液压阀换向，MRD粘滞力须小于双稳态永磁操动机构在0时所受的力F2，即小于22.2575 N，这是设计MRD的首要条件；

(2) MRD所能产生的最大阻尼力(最大阻尼力受电磁线圈导线线径所能通过最大电流及MRF的磁饱和强度的影响，并不是无限增大的)须和双稳态永磁操动机构在5 ms时所受得力大小差距不大。

由于所设计的双稳态永磁操动机构最大冲击力只有280.9853 N，且需要来回往复的换向，因此单线圈、双出杆、剪切阀式模型的MRD比较适合，且MRD的活塞杆直径不变。

该MRD的阻尼力可用式(1)表示[11]：

(1)

式中，Fτ—— 库仑力，N

Fη—— 粘滞力，N

L—— 阻尼通道有效长度，m

τy—— 磁流变液的屈服强度，kPa

h—— 阻尼通道间隙，m，一般取0.001～0.002 m之间

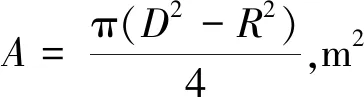
D—— 活塞直径，m

R—— 推杆直径，m

μ0—— MRF的零场黏度，Pa·s

由上述公式可知，MRD的阻尼力大小受到MRF性能、MRD结构参数等诸多参数的影响，本研究中仅分析不同大小阻尼间隙宽度对MRD阻尼力的影响，并选出最优的阻尼间隙宽度值。

MRD缸体材料选用电工纯铁DT4，活塞同样选用电工纯铁DT4，活塞杆由于和双稳态永磁操动机构的驱动杆做成一体式的，其材料选择为铜，MRD的电磁线圈选用0.5 mm线径的漆包线，匝数为500匝。所设计的MRD的磁流变液(MRF)采用美国LORD公司生产的MRF-132DG型磁流变液，该型号MRF具有响应时间较快、屈服强度可调范围较大、耐温性较好以及磨蚀性较低等优点。其基本技术指标如下：

零场黏度μ0(313 K)：(0.112±0.02)Pa·s

密度：2.95～3.15 g/cm3

MRF的B-H(磁感应强度-磁场强度)曲线、H-τ(磁场强度-屈服强度)曲线分别如图4、图5所示。

为了满足MRD小型化、MRD结构强度和阻尼力满足降低双稳态永磁操动机构冲击力的要求，对MRD的关键结构参数进行初始设计：阻尼缸体厚度8 mm[12]，有效阻尼通道长度12 mm，线圈匝数500匝，活塞直径28 mm，活塞长度23 mm。

2.2 MRD电磁场仿真及MATLAB数据处理及优化

确定了MRD的关键结构参数后，以阻尼间隙宽度h为自变量，由于阻尼间隙宽度一般为1～2 mm之间[13-14]，取h为1.1，1.2，1.3，…，2 mm，利用MATLAB软件分别计算其粘滞力的大小，从而选择合适的阻尼间隙宽度，图6所示即为计算所得的不同阻尼通道宽度h下的粘滞力Fη曲线，由计算结果可知：粘滞力的大小随阻尼通道宽度增大而减小，且在h=1.5 mm时，粘滞力大小为23.16 N，此时MRD即使不通电，其产生的粘滞力大于F2，故阻尼通道宽度须小于1.5 mm，由仿真结果可知，当h=1.6 mm时，粘滞力大小为19.08 N，此时小于F2，故阻尼通道宽度的大小需满足：1.6 mm≤h≤2 mm。

图4 MRF-132DG型磁流变液B-H曲线

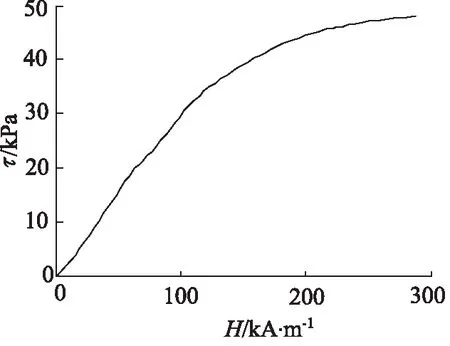
图5 MRF-132DG型磁流变液H-τ曲线

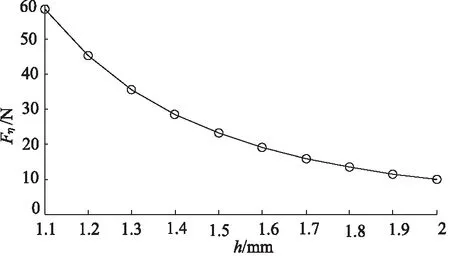
图6 不同阻尼间隙宽度的粘滞力曲线

然后分别对阻尼通道间隙宽度为1.6，1.7，1.8，1.9，2 mm的MRD进行Maxwell静磁场仿真，通过其磁场数值的大小来确定阻尼通道宽度的最优解。结合MRD结构尺寸，由于MRD是圆柱状对称结构，故在Maxwell里建立关于z轴对称的模型进行电磁场仿真。在线圈里分别通入大小为0，0.3，0.6，0.9，1.2，1.5 A的电流信号，并分别记录通入不同电流时所产生的对应的磁场强度，通过Maxwell仿真得到的不同阻尼间隙宽度h、不同电流I情况下的磁场强度H数据曲线如图7所示，可以看出：

(1) 随着阻尼通道的增大，相同电流下阻尼通道间隙越小，所产生的磁场强度越大，电流大于1.2 A时，MRD的磁场强度渐渐趋于饱和；

(2) 相同阻尼通道间隙的情况下，电流越大，所产生的磁场强度越大，且磁场强度会随着电流的增大逐渐趋近于饱和。

图7 不同阻尼间隙宽度的I-H曲线

利用MATLAB的cftool工具分别对这5个不同阻尼通道间隙的I-H曲线建立5个多项式拟合曲线方程，并利用MATLAB/Simulink建立I-H数学子程序。同样的方法对MRF-132DG型磁流变液的H-τ曲线建立多项式拟合方程，然后通过MATLAB/Simulink软件建立I-H、H-τ的模块子程序，由于MRF的屈服强度随磁场强度的增大而增大，因此可以建立起MRD所通入电流与其所产生的阻尼力的拟合程序，将这两个子程序集成到用同样方法建立的MRD的阻尼力公式(见式(1))的Simulink程序里，改变自变量电流的大小即可求得不同阻尼间隙宽度相对应的阻尼力大小。

由Simulink计算结果可得：阻尼间隙宽度一定的情况下，MRD的阻尼力随电流的增大而增大；电流一定的情况下，MRD的阻尼力随阻尼间隙宽度的增大而减小。当所通电流大小为1.5A时，阻尼间隙宽度分别等于1.6，1.7，1.8，1.9，2 mm时MRD的最大阻尼力分别为246.7，226.7，205.1，188.2，173.2 N，由于双稳态永磁操动机构的末端冲击力为280.9853 N，当阻尼间隙宽度为1.6 mm时MRD的最大阻尼力与双稳态永磁操动机构的末端冲击力差距是最小的，为了最大程度的调节并降低双稳态永磁操动机构的换向冲击力，故MRD的阻尼间隙宽度选为1.6 mm是最佳的。

仿真得到MRD的不同阻尼间隙宽度的阻尼力与电流之间的关系曲线(I-F曲线)如图8所示。

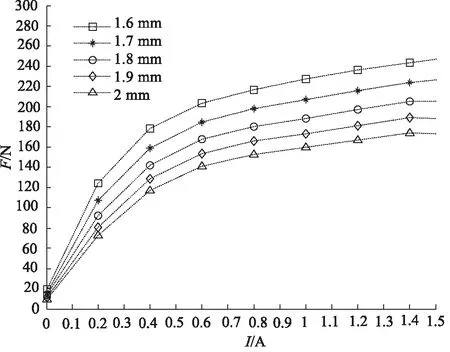
图8 MRD的I-F曲线

3 结论

(1) 设计了一种能够降低液压阀换向冲击力的带MRD缓冲的双稳态永磁电磁阀用驱动机构，双稳态永磁操动机构和MRD串联连接，为了防止双稳态永磁操动机构产生的磁场对MRD中MRF的影响，连接部分须加隔磁铜片；

(2) 双稳态永磁操动机构的作用是驱动阀芯实现换向和保持位。设计时首先根据所需要的永磁保持力及电磁换向驱动力的大小设计出双稳态永磁操动机构，通过Maxwell软件首先对双稳态永磁操动机构进行瞬态电磁场仿真，得到其换向过程中所受的最小及最大的电磁驱动力，以此作为设计MRD的可控阻尼力的调节范围；

(3) MRD的作用是调节、降低双稳态永磁操动机构的换向所带来的冲击力，在设计时需考虑工况和输出阻尼力的大小选择适合的结构模型，本研究为了较好的降低双稳态永磁操动机构的冲击力，其粘滞力须小于双稳态永磁操动机构的换向刚开始时的电磁驱动力，其最大阻尼力须和双稳态永磁操动机构的换向刚刚完成时的电磁驱动力相差不大，这样才能实现通过MRD调节双稳态永磁操动机构的冲击力的目的，经过仿真分析，MRD的阻尼间隙宽度为1.6 mm时，所设计的MRD的粘滞力和阻尼力可调范围均符合所希望达到的要求。