新暴雨特性下连云港市暴雨公式研究

王 欢，洪光雨，封一波

(江苏省水文水资源勘测局连云港分局，江苏 连云港 222004)

改革开放以来，中国城市化水平不断提高，与此同时，城市的快速发展带来的问题也很明显，城市的“热岛效应”、“雨岛效应”便是其中的典型，引起社会的广泛关注。

本文统计了连云港市市区1960—2012年降雨数据资料，见表1。

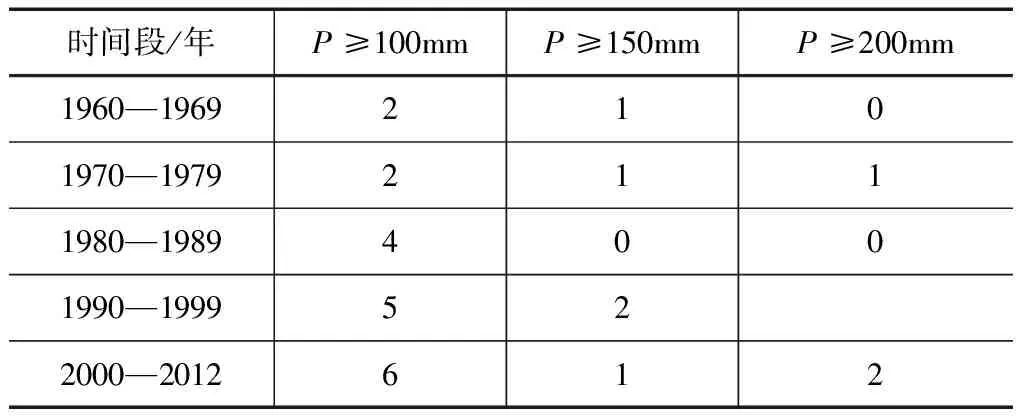
表1 连云港市市区1960—2012年暴雨发生频次记录表

由表1可知，进入80年代以来，随着城市化进程的加快，连云港市市区暴雨特性发生显著变化，暴雨频次明显增加。

暴雨公式是城市雨水排水系统规划与设计的基本依据之一，不同历时、不同重现期的暴雨强度是城市市政工程设计的重要设计参数。暴雨强度估算过大，将会导致排水排涝工程规模过大，造成浪费；反之，易造成内涝灾害，危害到经济建设和人们的生活。为了满足加强城市防洪需要，必须建立符合当地情况、当前城市气候和下垫面条件的暴雨公式，用来指导城市雨水系统进行规划、设计和管理。

1 技术路线

从连云港市雨量站网中选取代表雨量站，分析不同暴雨选样方法、分布模型及暴雨公式参数估计方法的优缺点，提出一整套适用于连云港市暴雨公式的编制方法，工作路线图如图1所示。

图1 工作路线图

2 设计暴雨分析计算

2.1 暴雨选样分析

(1)选样年份

选样年份应与连云港市暴雨特性的变化、雨量站观测仪器的更迭等相衔接。连云港市自进入80年代以来，市区暴雨特性发生显著变化；80年代起，水文部门雨量站观测仪器更改为虹吸式雨量自记，不再使用人工记录资料。综合以上因素确定暴雨选样年数为1981—2016年。

(2)选样方法

暴雨选样可分为年最大值法和非年最大值法，其中非年最大值法选样又分为年超大值法、超定量法及年多个样法。在暴雨公式研究中年最大值法及年多个样法运用较为广泛。

年多个样法选样是按不同历时每年取最大的6～8组雨样统一排序，再取资料年数的3～4倍的最大雨样作为统计的基础资料。该法不会遗漏较大雨样，较客观地反映了小重现期暴雨雨样的统计规律，可获得重现期小于1年的暴雨。但该法重现期概念不明，同时计算现代城市排水设计重现期较小部分的雨强意义不大，故该法的应用随现代城市的发展而减少。

年最大值法是各种历时每年选一个极值，其意义是一年发生一次的频率年值。该法独立性好，概念明确，当资料年份很长时，它近似于全部资料选样的计算值，其缺点是不能获得重现期1年及以下暴雨强度。由于该法资料易得，选样简单，国外于70年代就流行运用于城市暴雨公式的统计。

连云港市区代表站点资料系列较长，资料积累己远超过年最大值法的最低需要；另一方面，我国水利部门在暴雨选样中历来使用年最大值法，采用年最大值法进行暴雨取样可以与水利工程设计进行横向比较，克服了两者在暴雨频率互通性上的问题。综合考虑确定暴雨选样方法为年最大值法。

(3)暴雨历时

根据GB 50014—2006《室外排水设计规范》，暴雨公式计算降雨历时采用5、10、15、20、30、45、60、90、120min共9个历时，考虑到未来城市建设的不断加快，排水面积增大及城市规划的高起点，最高120min历时已不再满足城市发展的需要，因此，增加150、180min两个历时。

2.2 频率分布线型选择

频率分布曲线线型有多种。目前国内外最常见的水文计算概率分布曲线主要有3种，即极值(耿贝尔)分布曲线、指数分布曲线及皮尔逊-Ⅲ型分布曲线。以年最大值法选出的样本系列，分别选配上述三种频率分布模型，通过频率适线后的误差对比，优选暴雨资料的最佳适配线型。不同线型的误差统计见表2。

由表2可以看出，皮尔逊-Ⅲ型分布线型适配后的绝对均方差和相对均方差都最小，指数分布曲线次之，耿贝尔曲线最大。由此可见，对于连云港地区年最大值样本系列来说，皮尔逊-Ⅲ型分布曲线更适合。

2.3 参数估计

根据上述确定的样本系列(1981—2016年)、取样方法(年最大值法)、频率分布线型(皮尔逊(K.Pearson)Ⅲ型分布)进行目估适线。代表雨量站的短历时设计暴雨成果见表3。

2.4 设计成果

代表雨量站的短历时设计暴雨成果见表4。

将代表雨量站暴雨强度成果(i，t)点汇在双对数坐标纸上，代表站点暴雨强度i-历时t-重现期T关系如图2所示。

表2 不同频率分布线型适配误差统计

表3 代表雨量站频率适线参数成果表

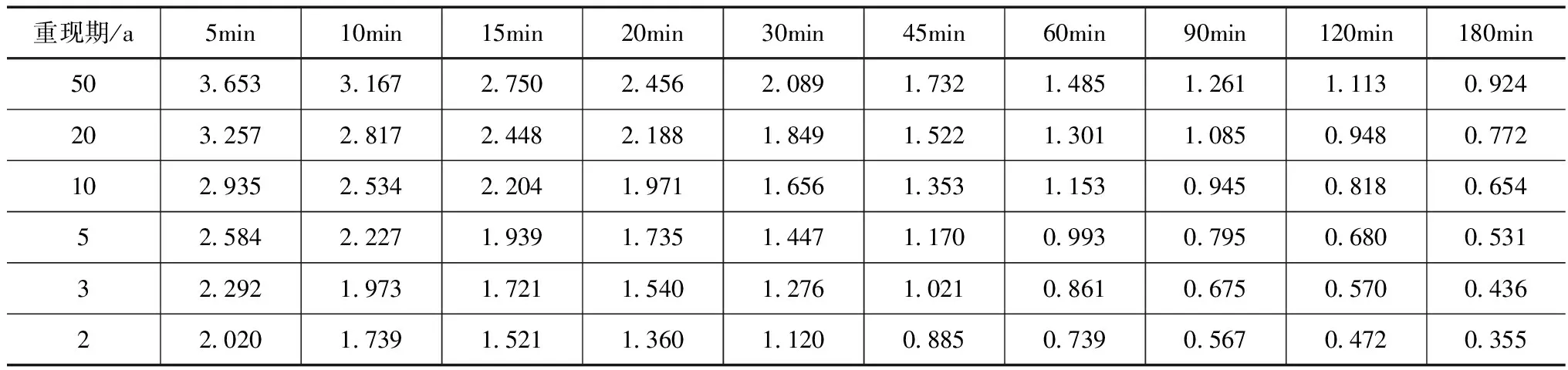
表4 代表雨量站暴雨强度成果表 单位：(mm/min)

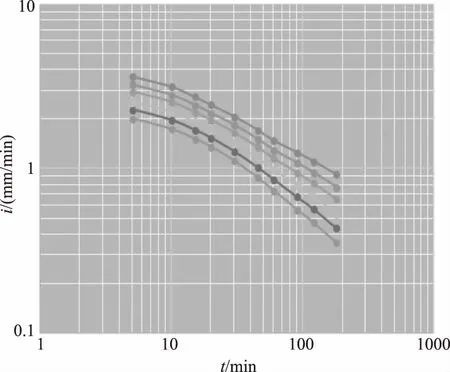
图2 代表雨量站暴雨强度i-历时t-重现期T关系图

3 暴雨公式推求

在暴雨强度公式推求中，最优化法有很多种。通过对比，分析目前比较流行的各种算法，如高斯-牛顿法、优选回归分析法、遗传算法等，发现各种算法在迭代计算次数有限的情况下，均得不到最优解，只能通过增加迭代次数来寻求最优解。在限定好暴雨公式各参数小数位数的情况下，寻优算法可以求出最优解，编程简单，易于操作。由于暴雨公式各参数取值范围不明确，即使采用先进的计算机程序来进行直接寻求最优解，完成一次运算也需要很长时间，因此，目前寻优算法不能简单拿来直接应用于暴雨强度公式编制。蚁群算法编程较为简单，可在Excel中通过简单的VBA编程实现，计算过程可见、可控，能相对容易的找出数条优选路径(即确定各个参数的取值区间)，结合寻优算法，在暴雨公式各参数小数位数确定的情况下，可以求出最优解。

以连云港市市区暴雨公式推求为例，在Excel表中，运用VBA小程序编制宏运算，在不知道各个参数取值空间的时候，尽量扩大取值空间。假设A1的取值空间是从1到100，n是从0.1到1.0，C是从0.1到1.0，b是从1到100，取100万只蚂蚁，均匀地放在A1取值空间1到100这条线路上，间距1，经过b，n节点，朝着目标均方差前行。即设置A1值是从1到100进行循环，循环步长取值1；C值是从0.1到1.0的范围进行随机取值，n值从0.1到1.0范围进行随机取值，b值是从1到50范围进行随机取值，均循环1万次，A1值和平均绝对均方差的关系如图3所示。

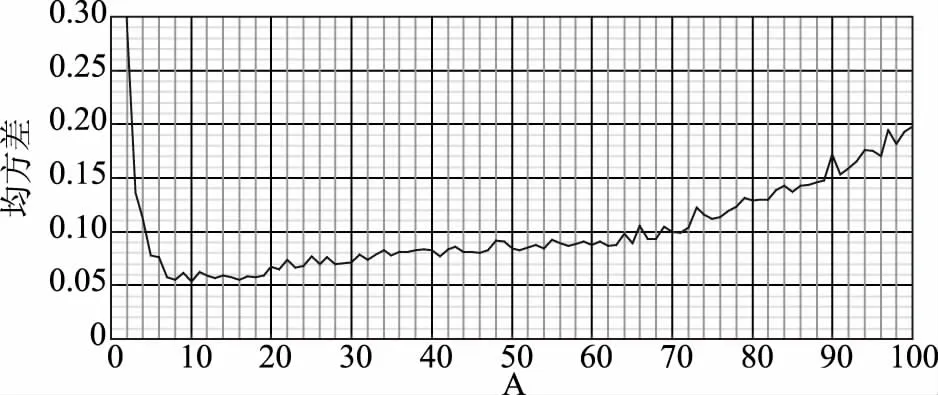
图3 暴雨强度总公式A1值与平均绝对均方差的关系图

由图3可以看出，随着循环次数的逐步增加，脉动的振幅逐步减小，A1值取值范围从5到20之间存在着最优解，相应C值的取值范围从0.62到0.87，n值的取值范围从0.47到0.84，b值的取值范围从3到24。然后，再次缩小各个参数的取值范围，加密循环的次数，运行到200万次时，A1值与平均绝对均方差的关系如图4所示。

图4 暴雨强度总公式A1值与平均绝对均方差的关系图

由图4可以看出，A1值取值范围在8到12之间存在最优解，C值的取值范围是从0.67到0.77，n值的取值范围是从0.58到0.69，b值的取值范围是从9到16。再次加大循环次数，运行150万次时，A1值与平均绝对均方差的关系如图5所示。

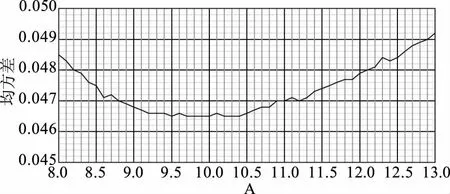
图5 暴雨强度总公式A1值与平均绝对均方差的关系图

由图5可以看出，A1值取值范围在9到11之间存在最优解，相应C值的取值范围是从0.714到0.736，n值的取值范围是从0.607到0.651，b值的取值范围是从10.6到13.0。可见A1、n、b、C这四个参数的取值范围再次压缩。用VBA小程序编制宏运算，在取值范围内，参数从最小值到最大值进行嵌套循环计算。通过多次试算的结果发现，由于A1、b、n、C各参数之间都是互相关联着，在A1值、b值的小数位数取1位的时候已经达到计算要求。为了实践应用方便，A1值、b值的小数位数取1位小数，c值、n值的小数位数取3位小数，最终得到代表站点的A1为9.5，b为11.2、n为0.619、C为0.719，平均绝对均方差最优解为0.0463mm/min。

4 暴雨公式成果

通过推求计算，连云港市市区暴雨强度公式为：

(1)

连云港市市区暴雨强度公式率定成果见表5。

表5 连云港市市区暴雨强度公式率定成果表

由表3可以看出，连云港市暴雨强度总公式的平均绝对均方差均不超过0.05mm/min，也就是说在高重现期暴雨强度较大的地方，它的平均相对均方差不超过5%，满足规范要求。

5 结语

推求暴雨公式时，采用蚁群算法率定暴雨强度公式参数，可建立A1与均方根误差最小值的关系曲线，辅助确定A1、C、b、n的取值区间，在取值区间内按A1、C、b、n循环顺序并由小到大取值循环搜索，结合寻优算法可有效避免最优解遗漏。该成果具有较高的实用价值，目前已被写入《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》，在编制暴雨公式时可以借鉴参考。