磁致伸缩扭转导波在纤维增强塑料锚杆中的应用
2019-05-21王明明孙晓云
董 永,王明明,孙晓云,王 莎,林 童
(石家庄铁道大学电气与电子工程学院,河北 石家庄 050043)
为解决锚杆的锈蚀问题,国外自20世纪90年代开始使用FRP锚杆来代替传统的钢铁锚杆,已在国内外矿山、隧道、公路边坡支护中得到了广泛的应用,但目前针对FRP锚杆的研究主要集中于力学性能,对其无损健康检测并不成熟[1-2]。磁致伸缩导波技术作为新型检测方式,克服了传统检测方式的局限性,具有非接触、距离长、无需耦合剂等特点,可对材料的健康状况进行快速、精确检测。
陈颖璞[3]对钢管内的纵向导波的位移、功率流分布特性进行了分析,指出纵向导波功率流平均分布于钢管内表面与外表面。何文等[4-5]通过仿真对扭转导波在锚杆中的底端效应及不同波速下扭转导波的传播特性进行了数值模拟得到了扭转导波检测最适频率。朱龙翔等[6]通过ANSYS对铝管内的扭转导波进行数值模拟,对含缺陷的铝管进行缺陷检测。HEINLEIN等[7]通过数值模拟验证了T(0,1)模态导波更适用于管道表面及周向缺陷检测。孙晓云等[8]设计了基于磁致伸缩的锚杆检测平台,将磁致伸缩导波技术应用于锚杆无损检测,在锚杆内激发并接收到了回波信号。KWUN等[9-10]将进行预先磁化的铁钴带与被检测管道进行耦合,并使激励线圈产生轴向的交变磁场,激发出了扭转导波。KIM等[11]将铁钴带与轴向成45°方向附着在被检测管道上激发出了扭转导波。磁致伸缩导波信号微弱、信噪比低,目前信号处理方式主要为小波变换、窗函数滤波等,但其对信号的抑制较为明显,不利于信号处理[12]。
磁致伸缩扭转导波应用于FRP锚杆将提高其检测精度。本文通过ANSYS有限元仿真建立了FRP锚杆的模型在FRP锚杆内激发扭转导波,分析了扭转导波在FRP锚杆内的传播特性;搭建了FRP锚杆物理实验平台,对有周向缺陷的FRP锚杆进行检测,通过FRP锚杆与镍带耦合的方式在FRP锚杆内激励并接收磁致伸缩扭转导波;针对电磁超声信号信噪比低、回波特征不明显的问题,采用CEEMD-LMS的滤波算法对电磁超声回波信号进行处理提升信号信噪比;通过实验结果验证磁致伸缩扭转导波检测方式可用于FRP锚杆无损检测。
1 扭转导波检测方式
1.1 扭转导波特性
磁致伸缩导波在FRP锚杆中的传播模态分为三种,纵向导波模态L(0,m)(L=1,2,…)、扭转导波模态T(0,m)(m=1,2,…)、弯曲导波模态F(n,m)(n,m=1,2,3,…),其中,n为周向阶数,m为导波模态[13]。L(0,1)模态磁致伸缩导波由于激发方式简单、传播速度快等特点,在锚杆锚固质量检测中应用更为广泛。L(0,1)纵向模态导波对锚杆周向缺陷检测更灵敏,但对锚杆外部锚固质量检测并不理想。
扭转导波T(0,1)激发方式较复杂,但在三种模态导波信号中是唯一非频散的[14],且在FRP锚杆内传播过程中能量衰减较小,其功率分布趋于FRP锚杆表面,适用于锚固质量检测。磁致伸缩导波信号微弱、信噪比较低,T(0,1)模态扭转导波在遇到FRP锚杆与锚固界面耦合处不会发生明显频散现象,且相较于纵向导波模态和弯曲导波更易于信号处理,FRP锚杆频散曲线如图1所示。
扭转导波在各向同性、均匀、弹性的FRP锚杆内传播时,存在周向位移uθ和剪切力τrθ,其运动方程见式(1)~(4)[15]。
uθ=[AZ1(qr)+BW1(qr)]ei(ωt-kz)
(1)
τrθ=-μq[AZ2(qr)+BW2(qr)]ei(ωt-kz)
(2)
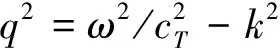
(3)
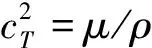
(4)
式中:r为FRP锚杆的半径;μ为FRP锚杆的剪切模量;A和B为常量;e为自然对数;cT为FRP锚杆的横波速度;ω为圆频率;ρ为FRP密度;Zn和Wn为线性无关的贝塞尔函数;k为轴向的波数。
通过式(1)~(4)计算L(0,1)模态导波、T(0,1)模态导波在FRP锚杆内的位移、功率流分布,其中激励信号频率为30 kHz,FRP锚杆半径为10 mm,结果见图2和图3。由图2可知,L(0,1)纵向模态导波,在FRP锚杆内传播只存在轴向位移uz和径向位移ur,径向位移ur比轴向位移uz较大,功率流平均分布于FRP锚杆轴心到半径之间。

图1 FRP锚杆频散曲线Fig.1 Dispersion curve of FRP bolt
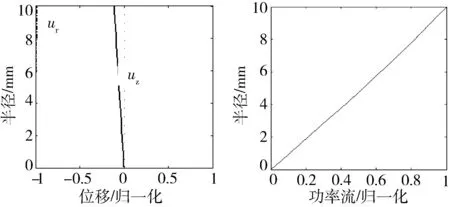
图2 30 kHz L(0,1)导波功率流和位移分布Fig.2 30 kHz L(0,1) guided wave power flow anddisplacement distribution
由图3可知,T(0,1)模态扭转导波在FRP锚杆中传播时只存在周向位移uθ,功率流分布从FRP锚杆半径6 mm起快速增大,功率能量更趋向于外表面。FRP锚杆缺陷多为锚固质量缺陷,通过磁致伸缩导波在FRP锚杆内传播可检测FRP锚杆与锚固耦合程度进而判断锚固质量。扭转导波传播功率能量比纵向导波传播功率能量更趋于外表面,故扭转导波对FRP锚杆的周向缺陷及外部锚固的缺陷检测更灵敏。
1.2 FRP锚杆有限元模型
通过ANSYS软件建立数值模拟模型,FRP锚杆长度为196 mm,半径为10 mm,缺陷在距左端面134 cm处,密度为1 850 kg/m3,弹性模量为72 GPa,泊松比为0.21。对8节点的SOLID164六面体单元进行建模,并进行扫掠式网格划分,FRP锚杆ANSYS有限元仿真模型如图4所示。由于在ANSYS内8节点SOLID164六面体中无法设置周向位移,故各节点的X方向和Y方向设置位移方向,其中合成力方向在FRP锚杆周向的切线方向传播。

图3 30 kHz T(0,1)导波功率流和位移分布Fig.3 30 kHz T(0,1) guided wave power flow anddisplacement distribution
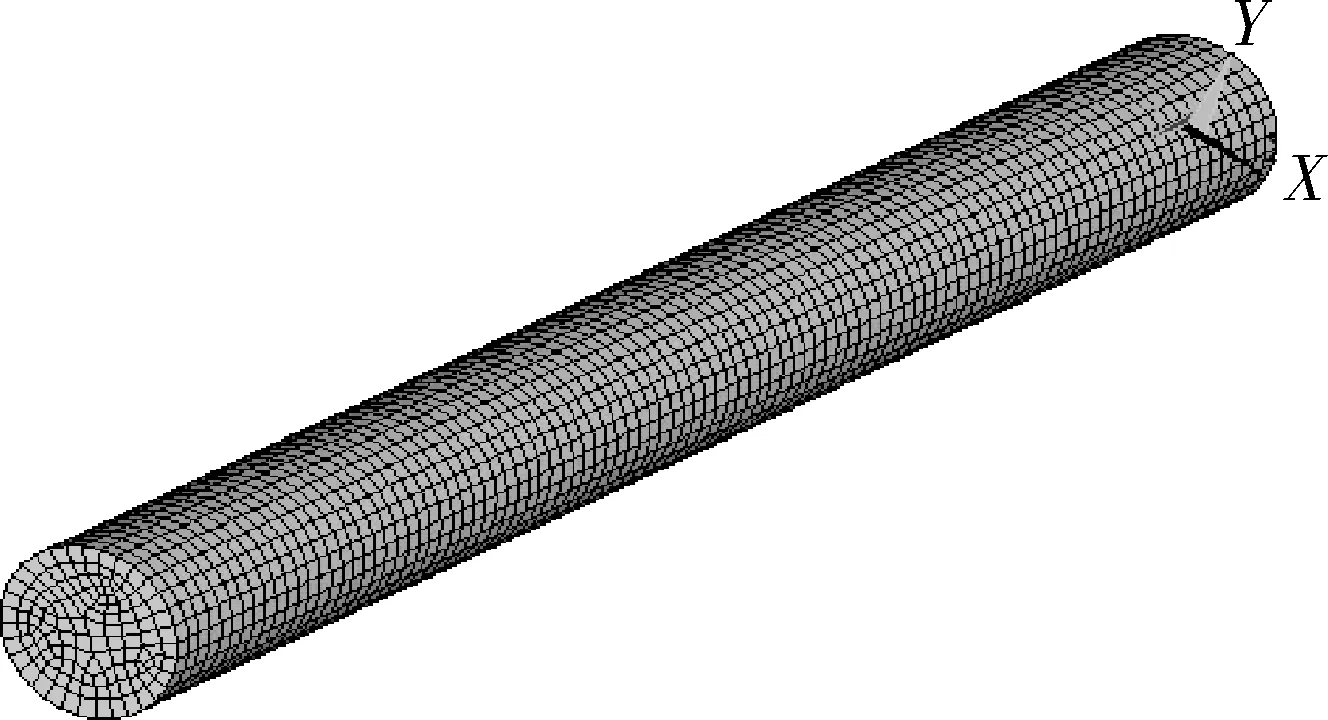
图4 FRP锚杆ANSYS仿真模型Fig.4 ANSYS simulation model of FRP bolt
在FRP锚杆顶端截面施加,激发信号为30 kHz正弦波信号。为验证公式计算中功率流在FRP内分布情况,将信号接收监测点取距轴心为4 mm的点A,与距轴心为9 mm的点B,图5和图6为数值模拟得到的A点和B点接收到的加速度信号。由图5和图6可知,B点第一次端面峰值与A点第一次端面峰值幅值比约为9∶1,与图3所示的功率流分布相近,由此证明扭转导波在FRP锚杆内传播功率更趋向于外表面。第一次端面与第二次端面回波相对时间差为1.33 ms,FRP锚杆长度为196 cm可得30 kHz扭转导波在FRP锚杆内的传播速度约为2 950 m/s。
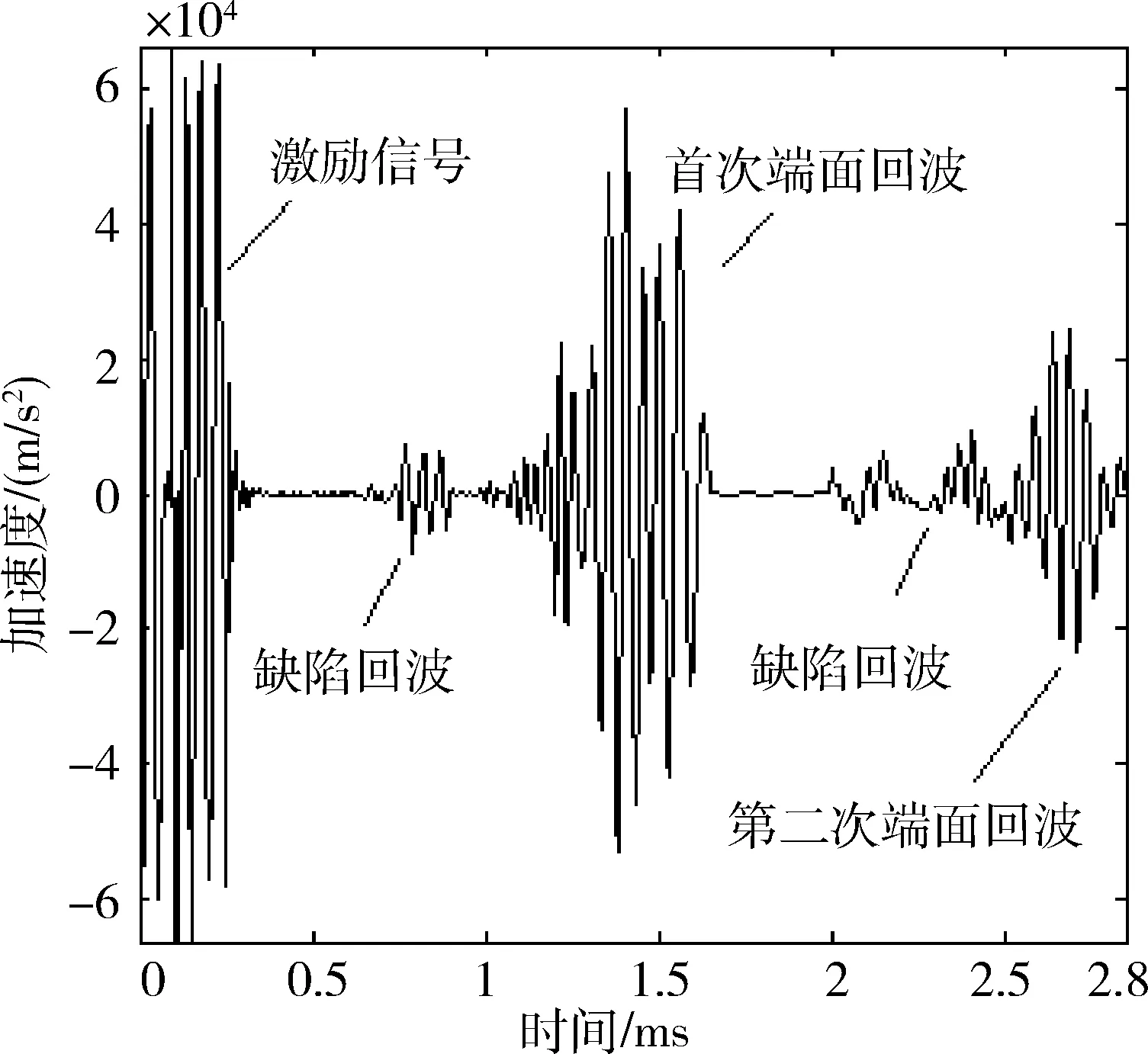
图5 A点回波信号Fig.5 A point echo signal
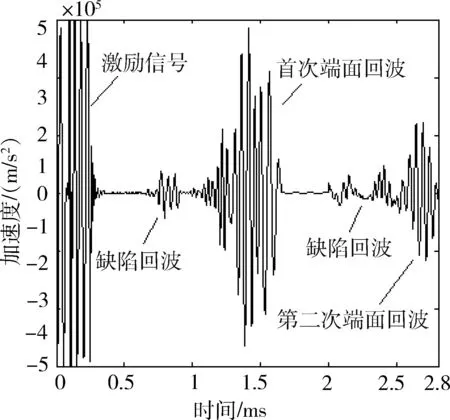
图6 B点回波信号Fig.6 B point echo signal
2 CEEMD-LMS算法
电磁超声信号检测中通常要求信号信噪比为16.5~20 dB,实验检测信号信噪比低,难以辨别回波特征需经信号处理。本文通过使用CEEMD与LMS结合的方式提高检测信号信噪比,使信号特征更明显。经验模态分解(EMD)将信号分解为数个含有瞬时物理意义的内敛模态函数(IMF),但经验模态分解中相似尺度信号可能存在于不同的IMF分量中不利于信号处理。DEERING等[16]通过对原始信号加入淹膜信号的方法均匀原始信号极值点的分布,从而解决了分解中模态混淆的问题。WU等[17]提出了集合经验模态分解(EEMD),即对原始信号加入辅助白噪声使不同尺度的信号连续。
2.1 CEEMD基本原理
经过集合经验模态分解后的信号随机白噪声较强无法彻底滤除,YEH等[18]提出了互补集合经验模态分解(CEEMD),即对加入原始信号加入大小相等,方向相反的辅助白噪声进而消除信号中剩余的辅助噪声。CEEMD将两对符号相反的白噪声加入原始信号,再进行EMD分解,将分解的结果进行组合可得最终的IMF信号,抑制了白噪声中和不完全的问题。
其具体算法步骤如下所述。
1) 将原始信号加入K组正负成对的白噪声,得到两套IMF共2K个信号,计算公式见式(5)。
(5)
式中:x(n)为原始信号;wk(n)(k=1,2,3,…,K)为白噪声;x+、x-分别为正、负成对的加噪后信号。
对集合中的各个信号分别做EMD分解,各个信号能产生一组IMF分量,其中第k个信号的第j个IMF分量表示为ckj。
2) 通过多组分量组合的方式得到的分解结果,计算公式见式(6)。
(6)
式中,cj为CEEMD分解后得到的第j个IMF分量。
2.2 LMS基本原理
LMS在随机输入维纳滤波器递归计算中使用确定性梯度,使用准则为滤波器实际输出值与期望响应之间的均方误差为最小,其具体迭代公式见式(7)和式(8)。
e(n)=d(n)-XT(n)W(n)
(7)
W(n+1)=W(n)+2μe(n)X(n)
(8)
式中:W(n)为LMS滤波器在时间n的权矢量;x(n)为原始输入信号;L为LMS滤波器的长度;μ为步长因子;d(n)是期望输出值;e(n)为误差信号;X(n)为时间n的输入信号矢量;v(n)为干扰信号;v(n)为自适应滤波器反馈值。
2.3 CEEMD-LMS算法
将CEEMD与LMS算法进行组合,CEEMD算法将信号进行分解,LMS对分解后的信号进行逐层滤波并重构。
CEEMD-LMS算法实现步骤如下所述。
1) 将原始信号加入正负成对的白噪声,产生两对信号集合。
2) 进行EMD分解,得到两组IMF分解信号。
3) 根据最小均方差LMS算法进行逐层滤波。
4) 将滤波后的IMF信号进行重构。
3 扭转导波实验检测系统
3.1 检测系统原理
纤维增强型塑料(FRP)锚杆本身不具有磁致伸缩性,在FRP锚杆表面用改性丙酸脂耦合若干镍带条,镍带条与FRP锚杆轴向成45°夹角,在交变磁场的作用下发生磁致伸缩现象,镍带条会沿FRP锚杆轴向45°方向伸缩,从而激励出切向FRP锚杆轴向45°的扭转导波。由于与镍带的耦合,FRP锚杆也会产生对应的扭转导波,扭转导波在FRP锚杆内传播,遇到缺陷或端面进行反射,反射回波传播到信号接收端时由于逆磁致伸缩效应,镍带伸缩将产生交变磁场,经由磁致伸缩换能器转换为电信号,将采集到的电信号经过信号调理电路放大再传入上位机,检测流程如图7所示。
3.2 实验检测系统
激励端、接收端分别用镍带通过改性丙烯酸脂沿FRP锚杆轴向45°进行耦合,镍带宽度为5 mm,长度为21 mm。在FRP锚杆外缠绕偏置线圈,漆包线直径0.41 mm,长度为7.5 cm,偏置线圈内通入0.7 A直流电流。因FRP锚杆不具有铁磁性故偏置线圈产生的磁场不会激发出纵向导波。偏置线圈外缠绕激励线圈、接收线圈,漆包线直径分别为0.51 mm、0.31 mm长度分别为6.5 cm、3.5 cm,激励端、接收端结构如图8所示。
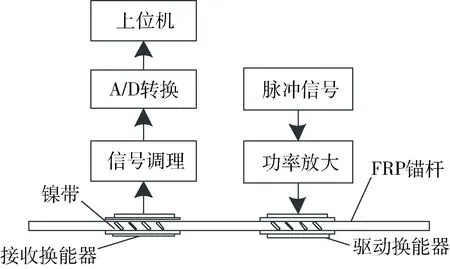
图7 FRP锚杆检测流程图Fig.7 FRP bolt detection flow chart

图8 磁致伸缩换能器结构Fig.8 Magnetostrictive transducer structure
实验室现有自由FRP锚杆长度为196 cm,将磁致伸缩换能器激励端中心置于距左端面68 cm处,接收端中心置于距左端面28.5 cm处;在距左端面134 cm处,沿周向方向有一个深度为4 mm且宽度为1.5 mm的缺陷。激励端通入30 kHz的2周期脉冲正弦波,触发间隔为3 s,实验检测系统如图9所示,上位机采集得扭转导波在FRP锚杆内传播的原始信号如图10所示。

图9 FRP锚杆实验检测系统Fig.9 FRP bolt test system
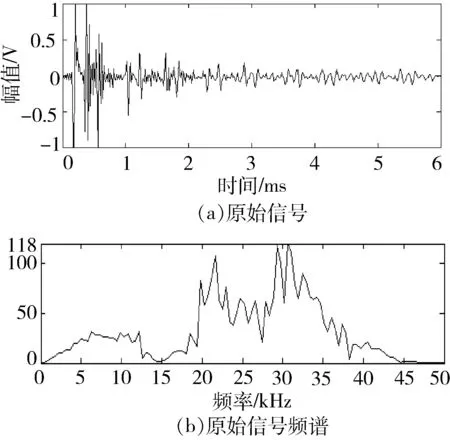
图10 接收换能器采集原始信号与信号频谱Fig.10 The receiving transducer collects the originalsignal and the signal spectrum
3.3 缺陷检测
由FRP锚杆检测系统采集到的回波信号信噪比约为8 dB,无法辨别回波信号特征。首先,使用传统的EEMD算法将原始信号进行分解,再用LMS自适应滤波算法将分解的各层信号滤波后重构,重构后信号如图11所示。经EEMD-LMS算法处理后的信号,因EEMD分解前需加入白噪声分解效率低,重构后白噪声使降噪效果较差,信号特征抑制明显,无法精确判别时域回波位置不利于检测。
相较于EEMD,CEEMD加入的为正负成对的白噪声,提高了计算效率且更适合于信号重构,重构后白噪声滤除效果明显。图12为CEEMD-LMS处理后信号。经CEEMD-LMS处理后的信号信噪比约为21 dB,满足检测要求且回波特征明显可对时域信号回波位置进行精确判断。

图11 EEMD-LMS处理后信号与信号频谱Fig.11 Signal and signal spectrm afterEEMD-LMS processing

图12 CEEMD-LMS处理后信号与信号频谱Fig.12 Signal and signal spectrum afterCEEMD-LMS processing
FRP锚杆中超声导波传播在频率为30 kHz时,T(0,1)导波在FRP锚杆中的传播速度约为2 950 m/s。从图12(a)中反射波形可得,右端面一次回波与首波相对时间为0.000884 s,计算距离为130.4 cm,与实际FRP锚杆相差2.4 cm;设置缺陷回波与首波相对时间为0.00044 s,计算距离为64.9 cm,缺陷相对激励端位置实际距离为66 cm,误差为1.05 cm。对实验室内2号FRP锚杆、3号FRP锚杆进行检测,其中,2号FRP锚杆长度为1.5 m,缺陷距激励端为40 cm,3号FRP锚杆长度为2 m,缺陷距激励端为95 cm,1号FRP锚杆、2号FRP锚杆、3号FRP锚杆检测实验结果见表1。根据锚杆无损检测规范要求,应力波反射法锚杆健康状况检测误差一般为实际值的5%,本检测系统检测误差约为1.5%,优于传统的应力波反射检测方法,误差满足检测要求。根据上述的实验结果分析,磁致伸缩扭转导波技术可应用于FRP锚杆的缺陷及长度检测。
通过搭建的FRP锚杆磁致伸缩扭转导波检测物理实验平台,其检测出的FRP锚杆长度、缺陷位置与ANSYS仿真模型结果相吻合。
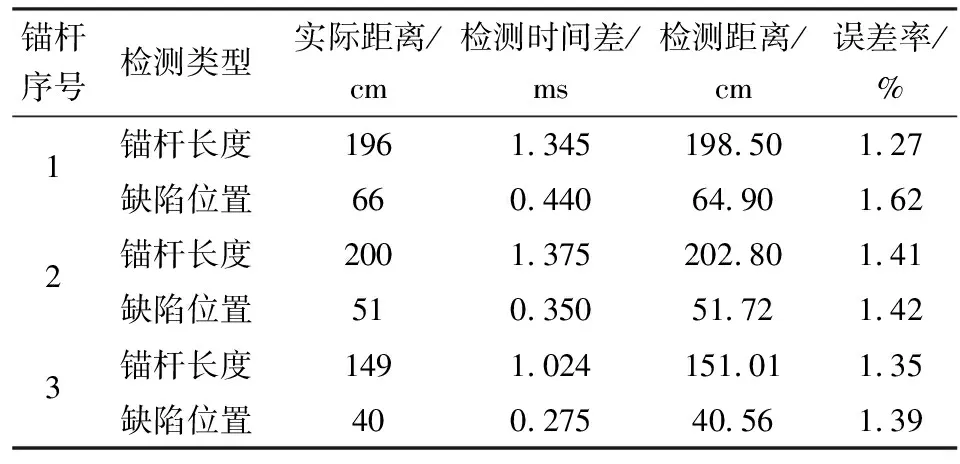
表1 实验检测结果Table 1 Experimental results
注:缺陷位置为距激励端距离
4 结 论
1) L(0,1)模态导波在FRP锚杆内传播功率流平均分布于轴心至外表面,T(0,1)模态波在FRP锚杆内传播功率更趋于外表面,证明了T(0,1)模态导波更适用于FRP锚杆锚固检测。
2) 经CEEMD-LMS算法滤波后的磁致伸缩导波信号相较于EEMD-LMS信噪比明显提升,滤波回波特征明显。
3) 通过实验验证,镍带与FRP锚杆耦合的方式可激励并接收磁致伸缩扭转导波,且能精确检测FRP锚杆长度及周向缺陷,检测精度满足工程要求。
