基于LM-BP神经网络的液压支架顶梁疲劳寿命预测及应用

李世科

(河南经贸职业学院计算机工程学院，河南 郑州 450046)

矿用液压支架在煤矿开采过程中能够维持顶板安全，保护矿工生命，是煤矿生产开采必不可少的机械设备[1-2]。然而在工作过程中由于长期承受交变载荷的作用，机械构件内部产生交变应力,使得液压支架顶梁的疲劳破坏成为支架破坏的主要原因之一。开展液压支架顶梁寿命预测，并采取相应的措施对煤矿的安全生产具有重要而现实的意义。通过梳理文献发现国内外学者针对矿用液压支架顶梁使用寿命的研究方法主要分为三类：一是基于力学理论的研究方法[3-5]；二是基于概率统计的研究方法[6-7]；三是基于信息技术的研究方法[8-9]。基于力学理论的研究方法常常使用经典的力学理论和有限元与累积损伤理论相结合，其中力学理论与累积损伤理论进行寿命预估的研究偏多[10]。基于概率统计研究方法的在进行研究时常常使用概率学、统计学的相关理论结合实验结果进行寿命评估[11]。基于信息技术的研究方法主要包括专家系统、遗传算法、模糊理论、人工神经网络等等[12]。以往的矿用液压支架顶梁的寿命预测大多是针对某一特定设计参数开展的研究，当设计参数发生改变时，需要重新进行疲劳分析建模，大大降低了生产的适用性。随着网络和信息技术的高速发展，人们拥有的信息和数据量成倍增长，利用数据挖掘技术揭示隐藏规律，从海量数据中提取有效信息成为解决生产和生活问题的重要手段。神经网络法是数据挖掘技术的一种重要方法，具有良好的自学习和联想储存功能，在寻找优化解方面具有独特优势。本文采用LM算法对BP神经网络算法进行改进，通过在ANSYS软件的Fatigue模块下建立ZY18000/25/45D液压支架疲劳分析模型，进行液压支架顶梁的寿命计算，为神经网络训练获取输入和输出参数。LM算法对BP神经网络算法改进后能够对不同设计参数下的液压支架顶梁进行寿命预测，实例表明该方法预测精度高，能够满足矿场应用的需求，对开展液压支架顶梁疲劳寿命预测具有一定的理论和现实意义。

1 基于LM的BP神经网络

1.1 BP人工神经网络

BP神经网络是基于BP算法的多层前馈网络，通过误差的反向传递对网络进行不断训练，在相对误差函数梯度下降的方向上不断调整网络权值，向所求目标逼近，是一种典型的有监督的学习算法[9-11]。BP神经网络包括输入层、隐含层和输出层，其中隐含层可以包含多层网络，其三层网络结构如图1所示。

图1 三层BP神经网络结构图Fig.1 Structural chart of three-layer BP neural network

设y是BP神经网络的输出，Oi为i节点的输入，N个样本点(xk,yk)(k=1,2…N)的网络输入是xk,网络输入是yk,任一节点j的输出可以用netjk表示,见式(1)。

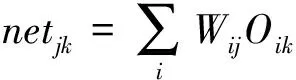
(1)

用E来表示平方误差函数，见式(2)。

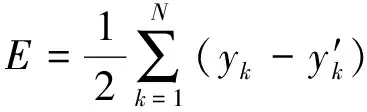
(2)

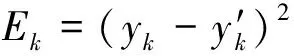
(3)

Ojk=f(netjk)

(4)

f(x)的表达式为式(5)。

(5)

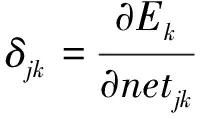
(6)

通过推导可以得出式(7)。

(7)

综上，可得到式(8)。

(8)

1.2 基于LM算法的BP神经网络

LM算法是Levenherg-Marquardt的简称，该算法在优化神经网络训练均方误差方面具有较强的适用性。在三层BP神经网络中应用时，LM算法可表示为式(9)和式(10)。

xk+1=xk-[JT(xk)J(xk)+μkI]-1JT(xk)v(xk)

(9)

Δxk=-[JT(xk)J(xk)+μkI]-1JT(xk)v(xk)

(10)

式中，μk大于0，当其数值越大表示算法越接近最速下降算法，其数值越小表示算法越接近于高斯-牛顿算法。在BP网络训练中均方误差用来表征性能，当所有目标以相同的概率出现时，均方误差与所有目标的平方误差之和成正比，见式(11)。

(11)

vT表示误差向量，计算见式(12)。

vT=[v1v2…vN]=[E1,1E2,1…ESM,1E1,2…ESM,Q]

(12)

xT表示参数向量，计算见式(13)。

xT=[x1x2…xn]=

(13)

式中，N和n计算分别见式(14)和式(15)。

N=Q×SM

(14)

n=S1(R+1)+S2(S1+1)+

…+SM(SM-1+1)

(15)

雅可比矩阵可表示为式(16)。

J(x)=

(16)

当xl为偏置值时，见式(17)。

(17)

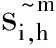
(18)

具体训练过程如下所述。

1) 在输入样本参数后，计算网络输出以及相应的误差和。

3) 计算Δxk,随后求取迭代计算平方误差和，当该值小于a中的误差和时，将μ除以θ,令xk+1=xk-Δxk,回到a；当该值大于a中的误差和时，将μ乘以θ，回到c步。直到梯度模小于某一数值时，结束运算。

2 液压支架顶梁疲劳寿命预测

2.1 顶梁设计参数的选取

顶梁、立柱和掩护梁共同承载顶板的压力，是液压支架的重要部件。顶梁在液压缸的支撑下进行工作，顶梁柱窝承受支撑力，同时承受来自于顶板的偏心力和扭转力，起到防止煤层塌陷的作用[13]。顶梁是一个由筋板、盖板等焊接而成的复杂的箱体结构，由于焊缝对受力影响较小，为了便于计算，忽略焊缝的影响[14]。网格数量的划分一方面受到计算精度的影响，另一方面受到分析时间的影响，划分网格单元要保证计算效率，同时也要能够真实可靠地反映顶梁危险点的受力情况。网格单元大小选用30 mm，顶梁材料选用Q690，其密度为7 800 kg/m3，屈服强度为680 MPa，抗拉强度为760 MPa，弹性模量为209 GPa。通过建立全参数化的顶梁模型简化计算的复杂程度，来提高有限元的计算效率。按照《煤矿用液压支架通用技术条件》(MT 312—2000)标准放置垫块，以此来模拟液压支架各种不同运行状况下的受载情况。液压支架的设计参数、载荷大小和作用方式是液压支架顶梁寿命的关键。

顶梁优化模型的第1个约束条件是变量的上下限。在循环载荷的作用下，循环载荷次数超过疲劳寿命时也会产生疲劳失效，本文选取的第二个约束条件是顶梁疲劳寿命次数N=3×104。数学表达式为式(19)。

xi,min≤x≤xi,maxi=1,2,3,4,5

σ(X)-σN≤0

(19)

式中：xi,min和xi,max分别为设计变量的上下限；σ(X)为顶梁最大应力值；σN为疲劳寿命次数N对应的疲劳应力值。

液压支架顶梁的工作周期是循环往复的，在一个周期内包含加载期、稳压期和卸载期三个时间段，分别用t1、t2和t3表示。在编制顶梁应力谱计算顶梁疲劳寿命时采用《煤矿用液压支架通用技术条件》(MT 312—2000)标准。设σN表示加载载荷为10 800 kN的应力，则P1=0.25σN,图2显示不出来。P2=1.05σN应力谱见图2。

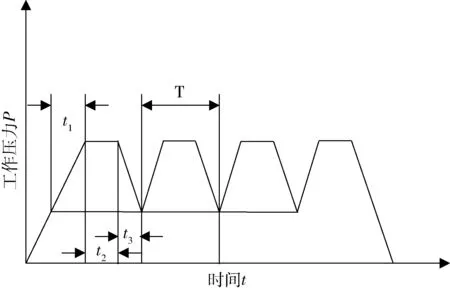
图2 顶梁应力谱Fig.2 Stress spectrum of roof beam

循环载荷的平均应力σm/MPa应力幅值σa/MPa和应力比r可以在图2中得到，其数学表达式为式(20)和式(21)。

(20)

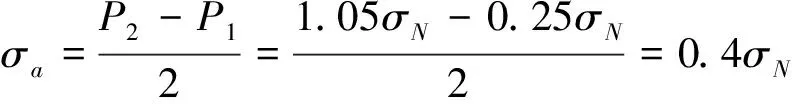
(21)

σm-N曲线用于计算对称循环应力，由于当r=0.24表示非对称循环应力，要采用Goodman方程(σm/σ-1)+(σm/σb)=1,将r的值转化为-1，则σ-1见式(22)。

(22)

式中：σ-1为疲劳次数为N时的疲劳应力；σb为材料屈服强度。用幂函数表达顶梁σ-N曲线为式(23)。

(23)

式中：材料参数k=3/1g1.8;常数C=(0.9σb)k×106;通过计算可以到当疲劳寿命次数N取得N=3×104次时疲劳应力的数值，其大小为554.8 MPa，并将此作为第2个约束条件。

为了符合实际情况，顶梁的设计参数的设置既要满足静力强度要求，同时也要保证顶梁的重量不能过大。在研究过程中，主要设计的参数取值范围如下：主筋板厚度为30～40 mm，柱窝上方中心处横版厚度为50～60 mm，两侧横板厚度为10～20 mm，导向套筒孔直径为75～85 mm，顶板厚度为25～35 mm。

2.2 液压支架顶梁疲劳寿命预测

基于LM的BP神经网络液压支架顶梁疲劳寿命预测过程如下所述，具体的操作流程如图3所示。

1) 确定研究对象，构建影响液压支架顶梁疲劳寿命预测的关键指标集。

2) 对各指标集进行归一化处理，见式(24)。

(24)

3) 利用BP神经网络对样本数据进行训练。

4) 采用LM算法对BP网络模型进行改进。

5) 开展模型预测效果评价，通过不断优化参数提高模型精度。

6) 利用训练好的模型对样本的液压支架顶梁疲劳寿命进行预测。

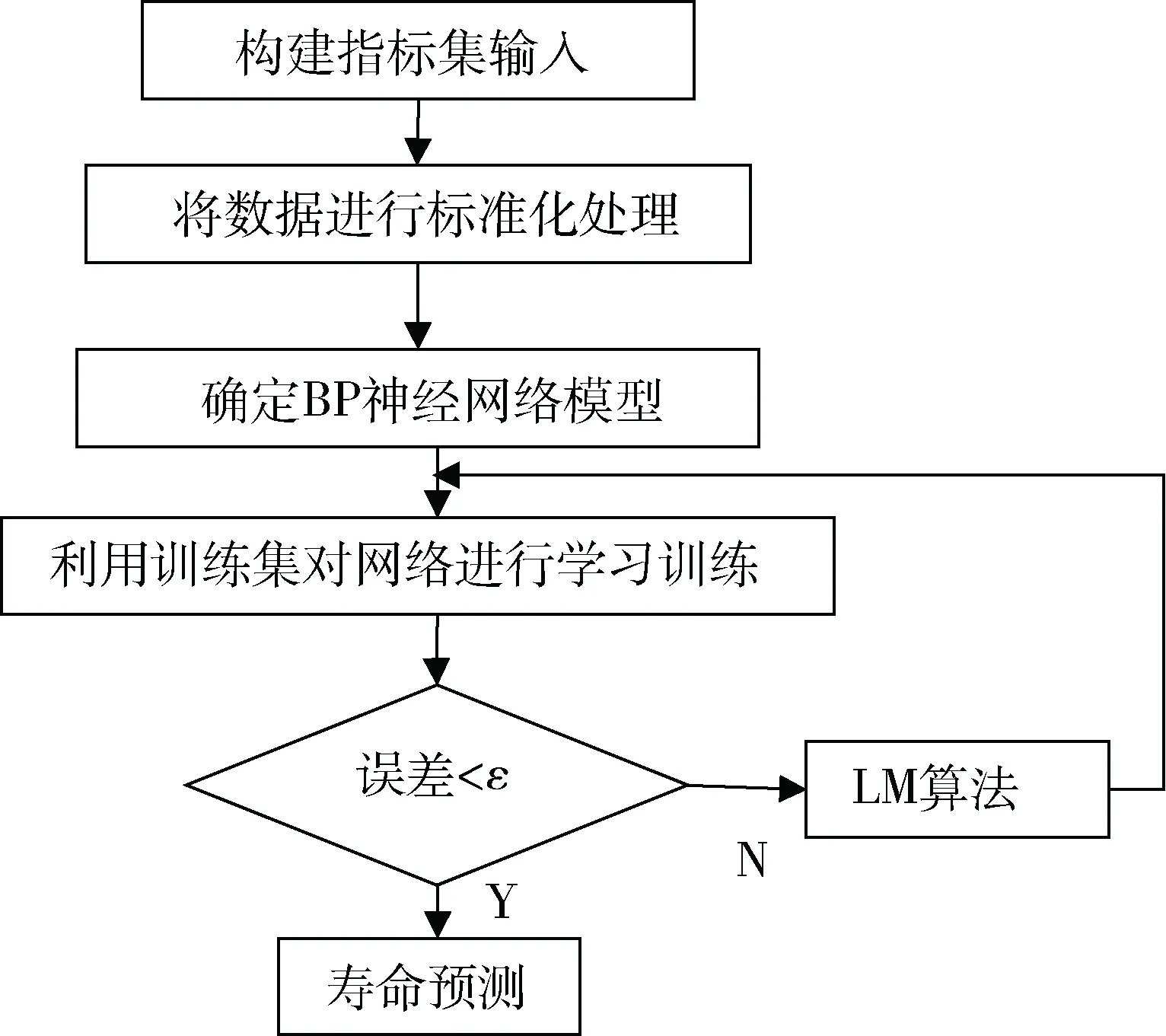
图3 液压支架顶梁疲劳寿命预测流程Fig.3 Fatigue life prediction process of hydraulicsupport top beam

3 实例应用

系统仿真的难度与设计参数和约束条件的数量成正比，为了更好地反映设计参数与疲劳寿命之间的关系，在实际中常常对没有必要的参数水平进行精简。本研究采用试验设计方法优化拉丁方选取样品点，在设计范围内总共选取了80个水平面上的参数点，软件集成平台在ANSYS的Fatigue模块下命令流文件进行疲劳寿命的计算，选取前70个作为训练集，后10个作为测试集，为了比较预测精度，另单独使用传统的BP神经网络对液压支架顶梁的疲劳寿命进行预测，两种模型的预测结果见表1。

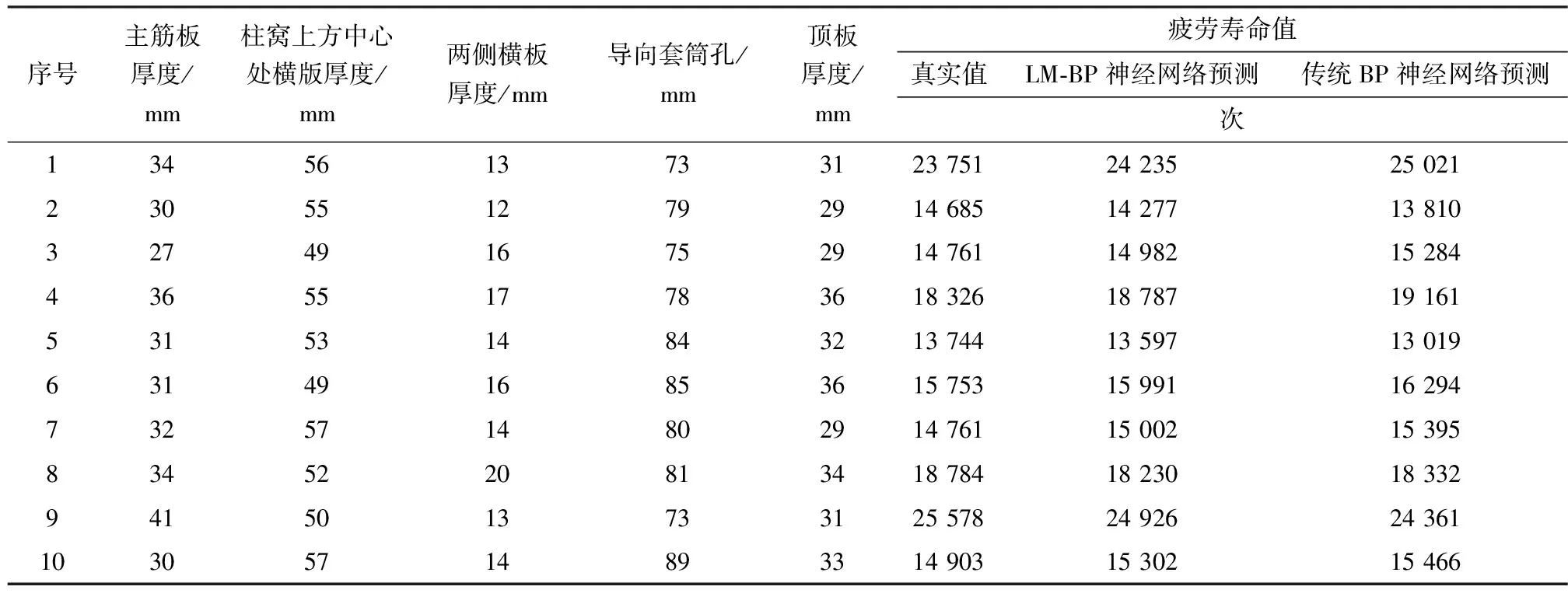
表1 顶梁疲劳样本点数据及其对应的疲劳寿命预测Table 1 Sample point data of beam fatigue and its corresponding fatigue life prediction

为了考察预测液压支架顶梁的疲劳寿命的预测精度，采用平均绝对误差、平均绝对百分误差(MAPE)和均方根误差(RMSE)三个指标来测定预测的精度，数值越小表明预测值和真实值之间的差异越小，预测精度越高，两种模型的预测精度指标表见表2。从表2可以看出，LM-BP神经网络的平均误差为0.16，MAPE值为2.12，RMSE值为411.32，这三个参数较传统BP神经网络相比相对较小，表明将LM算法引入到BP神经网络当中，能够有效地提高预测精度。

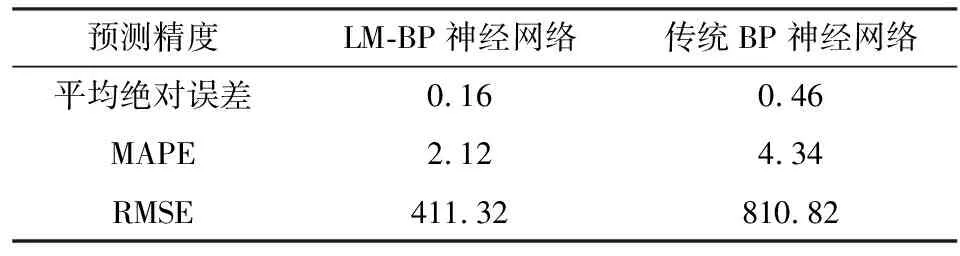
表2 不同预测方法预测精度对比Table 2 Comparison of prediction accuracy ofdifferent prediction methods

4 结 论

1) 本文利用LM算法改进BP神经网络开展液压支架顶梁的疲劳寿命，建立了包含主筋板厚度、柱窝上方中心处横版厚度、两侧横板厚度、导向套筒孔、顶板厚度五个参数的液压支架顶梁的疲劳寿命预测新方法，节省了时间、人力和物力。

2) 用10组样本点数据对本文的方法和传统BP神经网络方法的预测效果进行了对比，发现本文的预测方法误差相对较小，表明利用LM算法来优化BP神经网络能够有效地改善神经网络性能，可以用来进行液压支架顶梁的疲劳寿命预测，为有针对性根据实际情况优化液压支架顶梁参数提供了参考依据。