K-g-fusion框架的等价刻画

黄新丽

(福州理工学院文理学院, 福建 福州 350506)

Hilbert空间中的框架是Duffin和Schacffer[1]于1952年在研究非调和级数时引入的概念。 框架是标准正交基的一种推广，空间中的每个元素都能够由它线性表出，但它的重构表示式是不唯一的，这种冗余性使得它在实际应用中非常有用。 目前，框架理论已经在无线电通讯[2]、信号处理[3]等领域有着重要的应用。

随着框架理论的发展，出现了框架的不同形式的推广。 在处理巨大数据时，需要将一些数据做局部处理后再做整体处理，这种思想与计算机对大型数据处理时进行分部计算的方法相符合。 2004年，Casazza和Kutyniok[4]研究框架整体与局部关系时引入了Fusion框架的概念。 2006年，孙文昌教授[5]在已有的几种框架概念的基础上提出了g-框架的概念。 2011年，Gǎvruta[6]在研究原子分解系统时引入了一种推广框架——K-框架的概念。 一个序列fii∈I为H的K-框架的充要条件是其合成算子T满足R(K)⊂R(T)，而序列fii∈I为H的框架的充要条件是其合成算子T为满的，这说明K-框架与框架有许多性质是不一样的，因而K-框架具有重要的研究价值。 随后，一些学者提出了K-g-框架[7]、K-fusion框架[8]、K-g-fusion框架[9]的概念。 本文在原有的框架理论的基础上，研究K-g-fusion框架与其合成算子的关系，K-g-fusion框架与K-框架的等价刻画，以及K-g-fusion框架在算子扰动下的稳定性。 所得结论推广了一些已有的结论。

在本文中，设H和H′为两个可分的复Hilbert空间，Hii∈I是H′的闭子空间序列，其中I是正整数集的子集。 记L(H,Hi)为从H到Hi的所有有界线性算子的集合。 在本文中，算子Λi∈L(H,Hi)，其中i∈I。 定义l2({Hi})为

并定义其内积为

则l2({Hi})是一个复的Hilbert空间。

对任意的闭子空间V⊂H，算子πV表示H→V的正交投影算子。idH表示H上的恒等算子。L(H)是H到H所有有界线性算子的集合。 令K∈L(H)，且K≠0，用R(K)和NK分别表示算子K的值域和核。

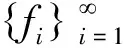
∀f∈H。

常数A和B分别称为K-框架的下界和上界。 特别的，当K=idH时，K-框架即为框架。

定义2[8]961设W=Wii∈I是H的闭子空间序列,K∈L(H),vi>0,i∈I. 如果存在正数A,B使得对任意f∈H有

则称{Wi,vi}i∈I是H的K-fusion框架.

定义3[9]3设W=Wii∈I是H的闭子空间序列,K∈L(H), Λi∈L(H,Hi),vi>0,i∈I。 如果存在正数A,B使得对任意f∈H有

(1)

则称{Wi,Λi,vi}i∈I是H的K-g-fusion框架。

当序列{Wi,Λi,vi}i∈I满足式(1)的右边时，序列{viΛiπWi}i∈I同时也是g-Bessel序列，可定义有界线性算子TΛ为

称TΛ为{Wi,Λi,vi}i∈I的合成算子。TΛ的共轭算子

称为{Wi,Λi,vi}i∈I的分析算子。

引理1[10]设L1∈L(H1,H),L2∈L(H2,H)，则下列命题等价：

1)R(L1)⊂R(L2)；

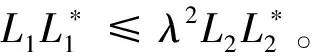
引理2[11]设H1和H2是两个复Hilbert空间，T:H1→H2是具有闭值域的有界线性算子, 则

‖T+‖-1‖f‖≤‖T*f‖≤‖T‖·‖f‖,f∈R(T)。

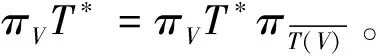
定理1设Wii∈I是H中的闭子空间序列，vi>0，i∈I，则下面两个条件等价：

1){Wi,Λi,vi}i∈I为H的K-g-fusion框架；

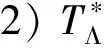
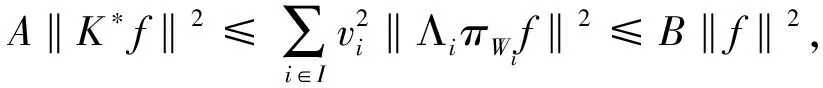
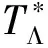
由引理1得R(K)⊂R(TΛ)。

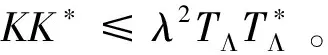
因此，{Wi,Λi,vi}i∈I为H的K-g-fusion框架。

当定理中的Λi=idH时，结论与文献[13]中的定理1一致。

文献[5]、[13]、[14]分别对框架与g-框架、K-框架与K-fusion框架的等价关系进行了讨论，下面本文讨论K-框架与K-g-fusion框架的等价关系。

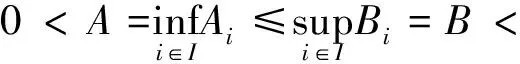
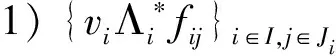
2){Wi,Λi,vi}i∈I为H的K-g-fusion框架。

证明首先因为R(K)为闭，R(Λi)⊂R(K)，由引理2得对任意的f∈H有

‖K*ΛiπWif‖2≥‖K+‖-2‖ΛiπWif‖2。

又因为ΛiπWi=πWiΛi，则对任意的f∈H有

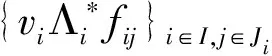
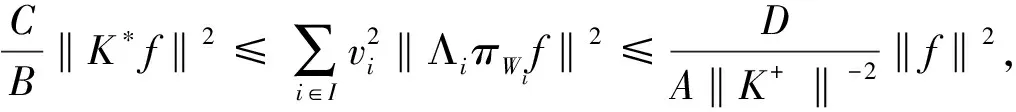
2)⟹1) 因为fijj∈Ji是Wi的k-框架，{Wi,Λi,vi}i∈I为H的K-g-fusion框架，所以存在正数C′、D′，使得对任意的f∈H，满足

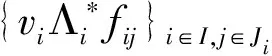
当Λi=idH时，算子K必须为满的，与文献[14]中的定理2结论一致。

下面讨论K-g-fusion框架在算子扰动下的稳定性。

定理3设{Wi,Λi,vi}i∈I是H中的K-g-fusion框架，上界、下界分别为B和A，如果T∈L(H)，ΛiπWi=πWiΛi且|I|<，则下列两个条件等价：

1){T(Wi),ΛiT*,vi}i∈I是H的TK-g-fusion框架。

2){T(Wi)}i∈I是闭子空间序列。

证明1)⟹2)直接由定义可得。

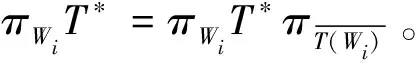
进一步，

而|I|<，故有界。 由定义3得{T(Wi),ΛiT*,vi}i∈I是H的TK-g-fusion框架。

当定理中的Λi=idH时，结论与文献[15]中的定理1一致。 文献[15]中举例说明了定理中的条件|I|<是必须的，否则结论不一定成立。

定理4设{Wi,Λi,vi}i∈I是H中的K-g-fusion框架，上界、下界分别为B和A，如果T∈L(H)，则下列两个条件等价：

1){T(Wi),ΛiπWiT*,vi}i∈I是H的TK-g-fusion框架.

2){T(Wi)}i∈I是闭子空间序列.

证明1)⟹2)直接由定义可得.

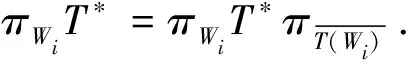
A‖(TK)*f‖2=A‖K*T*f‖2≤

B‖T*f‖2≤B‖T*‖2‖f‖2

由定义3得{T(Wi),ΛiπWiT*,vi}i∈I是H的TK-g-fusion框架.

该定理改进了文献[9]4中定理2.1.