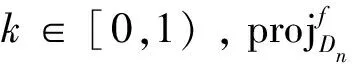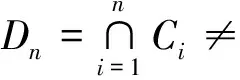Bregman拟严格伪压缩与均衡问题的强收敛定理及其应用

朱 胜, 黄建华

(1.福建农林大学金山学院, 福建 福州 350002；2.福州大学数学与计算机科学学院, 福建 福州 350116)

非线性领域很多研究课题，如极大单调算子的零元问题、凸可行问题、变分不等式问题、补问题和均衡问题等，都可归结成算子不动点问题来研究。关于算子的不动点理论的研究成果在物理学、规划问题、优化、经济均衡问题、微分方程等领域中已获得了广泛应用。因此，对于算子不动点问题的研究或建立某种算法在适当的条件下证明算法的强、弱收敛性的研究是十分有意义的。

在研究算子不动点问题时，有一类算子即非扩张算子是十分重要而且被广泛关注的。但是，在许多数学问题或实际问题的研究中，一些算子的非扩张性会随空间结构的改变而发生变化。如有些算子在Hilbert空间中是非扩张的，而在Banach空间中却不是非扩张的。为此，借助Bregman函数，对Bregman非扩张算子的不动点问题展开研究，使之将算子不动点理论推广到更一般的Banach空间。

2013年, ZHU J H等人[1]对均衡问题与Bregman强非扩张不动点问题的公共解问题提出算法:

2015年, WANG Z M[2]研究了Bregman拟严格伪压缩的不动点问题，提出算法:

受上述研究工作的启发,针对均衡问题和Bregman拟严格伪压缩映射的不动点问题的公共解,引入Bregman投影算法,在适当的条件下，得到强收敛定理。最后，把所得的结果应用到变分不等式问题，凸可行问题与极大单调算子的零点问题上，所得到的结果丰富了非线性分析中关于这一类领域的研究成果。

1 基本概念与引理

设E为实自反的Banach空间，E*为其对偶空间，E的范数记为‖·‖，E与E*的配对记为〈·，·〉，f∶E→(-,+]是真的实值函数，f的Frechet共轭函数f*:E*→(-,+]定义为f*(x*)=sup{〈x*,x〉-f(x):x∈E},x*∈E*。

记f的有效域为domf={x∈E,f(x)<},f的有效域内部为int(domf)。对任意的x∈int(domf)与y∈E,f在方向y的右导数定义如下：

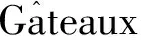
文献[3]给出了Legendre函数f∶E→(-,+]的概念，即f是Legendre函数当且仅当其满足下列条件：

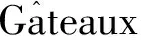
如果E为实自反的Banach空间,f为Legendre函数[4]，则：

1)f为Legendre函数当且仅当f*为Legendre函数;

2)(∂f)-1=∂f*;

4)f和f*在各自的有效域内部是严格凸的。

定义1[5]设f∶E→(-,+]为凸的可微函数，称Df:domf×int(domf)→[0,+)为关于f的Bregman距离

Df(y,x):=f(y)-f(x)-〈f(x),y-x〉。

值得注意的是Bregman距离并不是真正实际意义上的距离。易知,Df不满足对称性质和三角不等式性质。从Bregman距离的定义中容易得到四点等式性质：对任意的y、w∈domf与x、z∈int(domf)，有

Df(y,x)-Df(y,z)-Df(w,x)+Df(w,z)=〈f(z)-f(x),y-w〉。

定义2[6]设f∶E→(-,+]为可微的凸函数，点x∈int(domf)到非空闭凸子集C⊂domf上的Bregman投影为唯一的向量满足

定义3[7]设f∶E→(-,+]为可微的凸函数。称f是:

1)在x∈int(domf)全局凸的，若它在x的总体凸性模是正的，其中f在x的总体凸性模vf:int(domf)×[0,+)→[0,+)定义为

vf(x,t):=inf{Df(y,x):y∈domf,‖y-x‖=t}，∀t>0;

2)全局凸的，若对∀x∈int(domf)，f在x处都是总体凸的;

3)在有界集上全局凸，若对E的任何非空有界子集B和t>0，vf(B,t)均为正数，其中vf(B,t):=inf{vf(x,t):x∈B∩domf}为f在集合B上的全局凸性模。

引理1[7]称f∶E→(-,+]是序列一致的，如果对E中任意两个序列{xn}⊂int(domf)和{yn}⊂domf，当xn有界且满足时，有成立。f在有界集上是全局凸的当且仅当f是序列一致的。

引理2[8]设f∶E→(-,+]是一致Frechet可微的，且在E的有界子集上是有界的。那么f在E的有界子集上是一致连续的且f∶E的强拓扑→E*的强拓扑在E的有界子集上是一致连续的。

引理3[9]设f∶E→(-,+]是可微的全局凸函数。取x0∈E,如果序列Df(xn,x0)是有界的，则序列xn也是有界的。

引理4[10]设f∶E→(-,+]为可微的凸函数且在int(domf)上是全局凸的，x∈int(domf)，非空闭凸子集C⊂int(domf)，若z∈C,则下列结论等价。

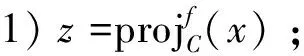
2)z是如下变分不等式的解：〈f(x)-f(z),z-y〉≥0,∀y∈C,即

〈f(x)-∀y∈C;

3)z是如下不等式的解：Df(y,z)+Df(z,x)≤Df(y,x),∀y∈C,即

∀y∈C。

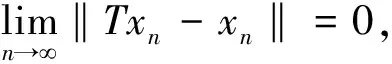
1)闭的，若对任意序列{xn}⊂C，满足xn→x∈C且Txn→y∈C(n→)，则Tx=y；

Df(p,Tx)≤Df(p,x),∀x∈C，p∈F(T)；

Df(p,Tx)≤Df(p,x),∀x∈C，p∈F(T)；

4)Bregman拟严格伪压缩的，若存在k∈[0,1)，且F(T)≠∅，使得

Df(p,Tx)≤Df(p,x)+kDf(x,Tx),∀x∈C,p∈FT。

容易看出：Bregman相对非扩张、Bregman弱相对非扩张都是Bregman拟严格伪压缩的。即,Bregman拟严格伪压缩是比Bregman相对非扩张、Bregman弱相对非扩张更一般的算子。

假设1 设C是一致凸和一致光滑的Banach空间E的非空闭凸子集，映射g:C×C→R为满足以下条件的二元函数：

1)g(x,x)=0,∀x∈C;

2)g是单调的，即g(x,y)+g(y,x)≤0,∀x,y∈C;

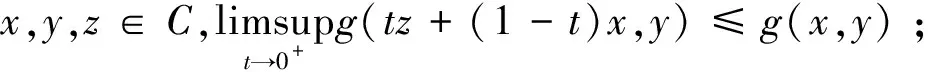
4)∀x∈C,g(x,.)是下半连续的凸函数。

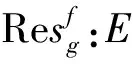
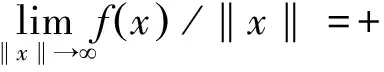
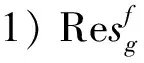
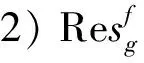
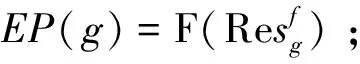
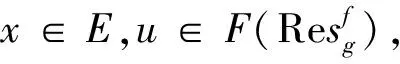
引理6[12]设f:E→R是Legendre函数且f*在int(domf)的有界子集上是有界的,取x∈E,如果序列{Df(x,xn)}是有界的，则序列{xn}也是有界的。

引理7[13]设C是实自反的Banach空间E的非空闭凸子集，f∶E→R为在E的有界子集上是有界的、一致Frechet可微的和全局凸的Legendre函数，T:C→C是Bregman拟严格伪压缩映射，则T的不动点集F(T)是C的闭凸子集。

引理8[13]设E是实自反的Banach空间，f∶E→R是Legendre函数，且在E的有界子集上是有界的、一致Frechet可微的。非空闭凸子集C⊂E，T:C→C为Bregman拟严格伪压缩映射，则对任意x∈C,p∈F(T),k∈[0,1)，有

引理9[14]设E为实自反Banach空间，f∶E→-,+是真的下半连续函数，则f*:E*→-,+是真的弱*下半连续凸函数。因此，对任意z∈E，有

2 主要结果

定理1 设E是实自反的Banach空间，f∶E→R是强制的Legendre函数，且在E的有界子集上是有界的、一致Frechet可微的和全局凸的。非空闭凸子集C⊂int(domf)，T:C→C为Bregman拟严格伪压缩闭映射。设g:C×C→R是满足条件1)-4)的二元函数。序列xn定义如下：

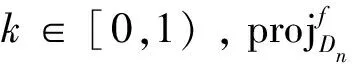
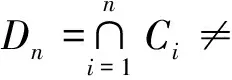
证明分为6步：

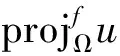
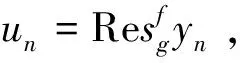
Df(v,f*(αnf(xn)+(1-αn)f(Txn)))≤αnDf(v,xn)+(1-αn)Df(v,Txn)≤

αnDf(v,xn)+(1-αn)[Df(v,xn)+kDf(xn,Txn)]≤Df(v,xn)+kDf(xn,Txn)。 (2)

因此，由式(2)又可得，

(3)

由四点等式性质知

Df(v,un)=Df(v,xn)+Df(xn,un)+〈f(xn)-f(un),v-xn〉。 (4)

把式(4)代入式(3)，可得

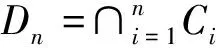
所以序列Df(xn,u)有界，再由引理3得序列xn有界。

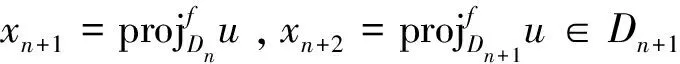
(5)

即

Df(xn+2,xn+1)+Df(xn+1,u)≤Df(xn+2,u)， (6)

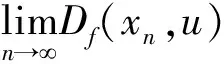
由于Dn是压缩的，对于任意的正整数m≥n，有Dm⊂Dn。

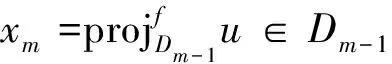
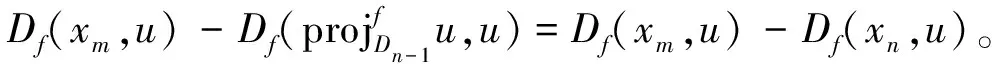
在式(7)中令

m,n→，可Df(xm,xn)→0，(m,n→)。 (8)

根据引理1的结论可知，

(9)

所以xn是Cauchy序列。

5)证明xn强收敛于Ω:=FT∩EP(g)中的一个点。因为E是自反的Banach空间，且xn是Cauchy序列。不妨假设

(10)

首先，证明x*∈F(T)。在式(9)中取m=n+1，则有

(11)

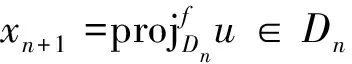
(12)

由xn是有界，得un有界。因为f是一致Frechet可微，由引理2有

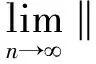
由于xn+1∈Cn和式(2)、式(3)，有

(14)

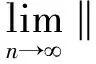
下面证明x*∈EP(g)。映射f是一致Frechet可微的，f在有界集上是一致连续的，由式(13)、式(15)知

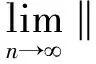
因为，g(un,y)+〈f(un)-f(yn),y-un〉≥0,∀y∈C。

由假设1的2)可得

〈f(un)-f(yn),y-un〉≥-g(un,y)≥g(y,un),∀y∈C。 (17)

在式(17)中令n→，再由假设1的4)与式(16)有

g(y,x*)≤0,∀y∈C。 (18)

对于任意的y∈C，取t∈(0,1]，令yt=ty+(1-t)x*∈C，则有g(yt,x*)≤0以及

0=g(yt,yt)≤tg(yt,y)+(1-t)g(yt,x*)≤tg(yt,y)。 (19)

所以有g(yt,y)≥0。进一步可得

∀y∈C。

即证得x*∈EP(g)。综合以上证明可得,x*∈Ω:=FT∩EP(g)。

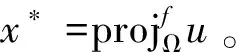
〈f(u)-f(xn+1),xn+1-z〉≥0,∀z∈Ω。 (20)

在式(20)中，令n→,有〈f(u)-f(x*),x*-z〉≥0,∀z∈Ω，即因此，序列xn强收敛于证毕。

3 结果应用

3.1 极大单调算子的零点问题

设E为实自反Banach空间，映射A·E→2E*是极大单调的，且A-10≠∅，f∶E→-,+为一致Frechet可微的，且在E有界子集上有界，则A相对于f的预解算子fx是Bregman相对非扩张闭映射[8]，从而也是Bregman 拟严格伪压缩的。根据定理1可得：

定理2 设E是实自反的Banach空间，f∶E→R是强制的Legendre函数，且在E的有界子集上是有界的、一致Frechet可微的和全局凸的。非空闭凸子集C⊂int(domf)，T:C→C为Bregman拟严格伪压缩闭映射。设g:C×C→R是满足条件1)-4)的二元函数。序列xn定义如下：

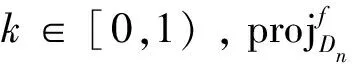
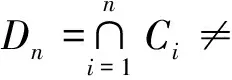
3.2 凸可行问题

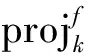
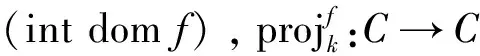
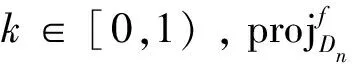
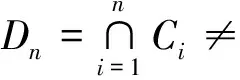
3.3 变分不等式问题

引理10[2]设f∶E→R是强制的全局凸的Legendre函数，满足ran(f-A)⊆ran(f)。设A:E→E*为Bregman反强单调映射[8]，若非空闭凸集C⊆(domA)∩(int domf)，则有下列结论

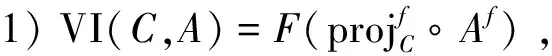
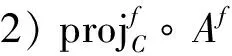
定理4 设E是实自反的Banach空间，f∶E→R是强制的Legendre函数，且在E的有界子集上是有界的、一致Frechet可微的和全局凸的，且满足ran(f-A)⊆ran(f)。A:E→E*为Bregman反强单调映射，非空闭凸子集C⊆(domA)∩(int domf)，T:C→C为Bregman拟严格伪压缩闭映射。设g:C×C→R是满足条件1)-4)的二元函数。序列xn定义如下：