基于模型预测控制方法的纯电动集装箱转运车横向运动分析

王汐文 鲁统利* 江 华

(1.上海交通大学机械与动力工程学院，上海 200240，E-mail: tllu@sjtu.edu.cn；2.上海振华重工(集团)股份有限公司，上海 200125)

0 引言

随着经济全球化日益加深，世界主要集装箱港吞吐量急剧增长，并且由于中国经济贸易的高速发展，我国量达21798万标箱[1]。庞大的集装箱吞吐量要求港口大港口集装箱吞吐量已远超欧美，2016年港口集装箱吞吐幅提高作业效率，也加速了自动化码头的建设进程。目前自动化码头中的水平作业多是由集装箱卡车完成。但为了提高效率，减少人力成本，适应自动化码头的需求，国内外开始研发各类大型自动导航电车(Large-Scale Automated Guided Electric Vehicle，简称LS-AGEV)。这是一种大型的AGV，可以装载集装箱在港口进行运输，装备有电磁或光学等自动导引装置，能够沿规定的导引路径行驶，具有安全保护以及各种移载功能的运输车。LS-AGEV具有无人驾驶、精确定位、自动导航、污染性小的特点，将逐步成为自动化码头的核心设备[2]。

由于AGV的逐步发展及应用，很多学者对其动力学分析及控制方面进行了广泛研究。陈猛等建立了自动导引车的动力学模型，利用MSC/Nastran仿真得到了AGV在加速行走和急停过程中的结构应力、变形及疲劳寿命[3]。陈卓利用MATLAB对AGV系统车体结构模型中的非线性耦合特性进行建模及分析[4]。葛红豆等为提高AGV运动控制效率，设计了模糊PID控制器，并经过对比验证了控制器的效果[5]。

本文的研究对象是上海振华重工最新研发的第三代集装箱转运车，拥有全轮电驱动、整车原地360度转向与电差速控制技术。横向运动是新型电驱动集装箱转运车的一大特点，可以在转运车到达指定地点时通过横向运动进行微调，从而准确到达集装箱装载或卸载的位置，也可以通过横向运动在行进过程中进行路线调整及避让其他车辆。但是由于其装载货物时车辆质心高，同时横向运动时轴距极大缩短，很容易在横向运动的过程中发生车辆俯仰倾覆的危险，因此需对其横向运动过程进行分析，保证其横向运动的稳定性。采用模型预测控制方法对集装箱转运车的横向运动进行控制。模型预测控制方法可以在一定的约束条件下，预测一段时间以后的系统响应，合理地计算控制量，从而可以得到每一个时间段的经过优化的输入量，进而对模型进行有效地控制[6]。本文建立了集装箱转运车的二自由度模型，以其横向加速度为输入，车身俯仰角为输出，在一定的约束条件下，控制其俯仰角的大小，保证其横向运动的稳定性。

1 纯电动集装箱转运车建模

1.1 车辆多体动力学模型

智能电驱动集装箱转运车是自动化码头关键配套设备，是一种全新概念的无人驾驶纯电动低速特种车辆，采用最新工业设计及环境感知智能控制技术，配备高精度多系统复合导航进行自动巡航、定位及防撞；由四个电机进行独立驱动并加以电差速智能控制，实现其灵活平稳运动；四轮独立线控转向机构可实现原地转向及横向平移，为装卸货物、避让车辆提供了极大的便利；悬架系统采用液压、橡胶系统组合减震，同时实现单车架整体升降，提高装卸货物的效率及运载货物的安全性。该设备为无人化运输机器人，拥有较大的载重自重比及较高的满载车速，使集装箱转运车更高效、更节能。其实物如图1所示。

图1 新型纯电动集装箱转运车实物图

转运车的UG模型如图2所示。转运车有四组双车轮，四组车轮之间独立驱动，转向机构为由电机驱动的一对齿轮组，可以实现线控360°转向，也正是这样的转向机构，实现了转运车的横向运动。由于港口码头集装箱转运车行驶的路面相对平整，车轮与车架之间由橡胶弹簧进行减震，液压缸用来完成集装箱的举升动作，从而进行装卸集装箱。转运车的相关参数如表1所示。

图2 转运车三维模型

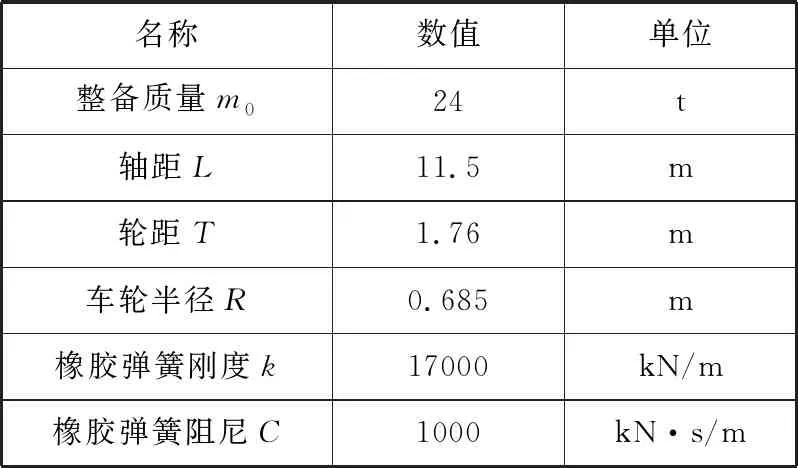
表1 集装箱转运车的基本参数

将UG模型进行适当地简化，去掉细节部分，仅保留其车架、悬架结构、转向机构与驱动机构，导入到ADAMS软件中，得到集装箱转运车的多体动力学模型，并为其装载40 t的货物，得到如图3所示的模型，并对其横向运动进行仿真。设定集装箱转运车从10 s开始横向运动，加速至车速为1 m/s，25 s开始减速至停止，得到的车速曲线如图4所示，从而验证了模型的正确性。

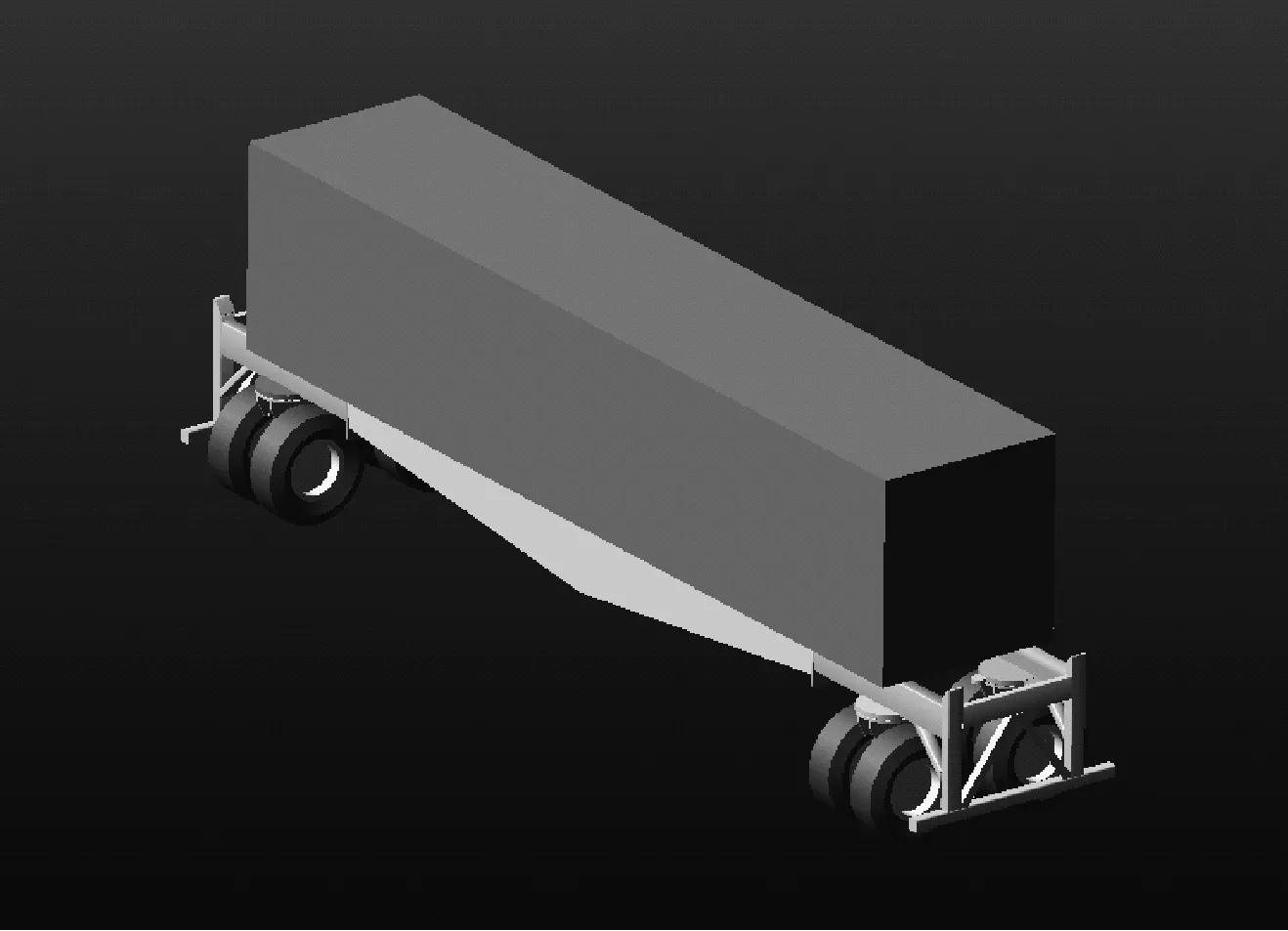
图3 转运车多体动力学模型

图4 LS-AGEV横向运动速度响应

从图5中可以看出，集装箱转运车在加速或减速过程中，车身的俯仰角会有一定的变化，若增加加速度数值，会造成更大的俯仰角，甚至导致车辆无法正常行驶。这是因为载货后车辆质心较高，当其横向运动时，原来较长的轴距则为轮距，而较短的轮距则为轴距。这时，由于车辆质心高，轴距短，很容易发生俯仰倾覆的情况，所以其横向运动的加速度不能过大，也不能过急。因此在其进行横向运动的时候，要对其横向加速度进行控制，从而保证其横向运动的稳定性。

图5 LS-AGEV横向运动车身俯仰角响应

根据转运车的轮距T=1.76 m、橡胶弹簧工作长度l=0.2 m，可以求出在几何约束上，车身俯仰角能达到的最大极限为

(1)

1.2 车辆动力学模型

图6描述了转运车的横向运动模型，其中，m是转运车质量，ay是横向运动加速度，φ是车身的俯仰角，h为车辆质心到侧倾中心的距离，Ft1、Ft2、Fz1、Fz2、Ff1、Ff2分别为前后车轮的驱动力、地面支持力和摩擦力。由此可得到运动方程为

(2)

图6 转运车横向运动模型

假设车辆按照图6所示的方向行驶，那么车辆不发生俯仰倾覆的条件为路面对前轮的支持力不为零，即

(3)

式中，h′为车辆质心到地面的距离。因此，我们需要设计转运车横向运动的加速度，使其车身侧倾角满足几何约束与运动学约束。

联立式(1)、式(3)，并代入h′=2.5 m，得到

(3)

即集装箱转运车在横向运动的时候，其加速度不得超过1.3 m/s2。

2 模型预测控制器设计

预测控制可以在保证控制系统的稳定性和鲁棒性的基础上，处理控制量的约束问题。本文利用基于状态空间的模型预测控制方法，根据车辆的运动状态和期望状态，规划车辆最优的横向加速度输入，从而保证转运车在横向运动中的稳定性。

(4)

将上述模型离散化后得到

(5)

其中，Ad、Bd为离散化的系统矩阵及输入矩阵。

对离散化模型进行改写，将输入状态u(k)写到状态变量中，得到下面的模型

(6)

(7)

取上个变量的差值[7]，得到

(8)

将y(k)引入到上述模型中，根据

因此有

(9)

为了使车辆的俯仰角满足约束，选取状态变量为

则有

ξ(k+1)=Aξ(k)+BΔu(k)

η(k+1)=Cξ(k)

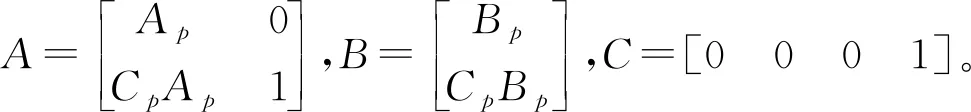
假设系统的预测时域长度为Np，控制时域长度为Nc，并且Np>Nc，则有

ξ(k+1|k)=Aξ(k)+BΔfu(k)

ξ(k+2|k)=Aξ(k+1|k)+BΔu(k+1|k)=

A2ξ(k)+ABΔu(k)+BΔu(k+1|k)

⋮

ξ(k+Np|k)=ANpξ(k)+ANp-1BΔu(k)+…+

ANp-Nc-1BΔu(k+Nc|k)

同样可以得到输出η的表达式

η(k+Np|k)=CANpξ(k)+CANp-1BΔu(k)+…+

CANp-Nc-1BΔu(k+Nc|k)

矩阵表示如下

Y(k)=ψξ(k)+θtΔU(k)

(10)

其中，

模型预测控制的性能指标为

(11)

Q=CTC×q

其中，ΔU(k)为k时刻的最优控制量；Q、R为权重矩阵,q为Q的权重系数。式中第一项表示对理想输出的跟踪能力，第二项表示对横向加速度的变化幅度的限制。

在每一个时间步长，需要解决以下最优问题：

(12)

s.t. ΔUmin≤ΔU(k)≤ΔUmax

Umin≤U(k)≤Umax

Ymin≤Y(k)≤Ymax

其中，U(k)和Y(k)的约束都可以转化为ΔU(k)的表达式，则上述三个约束都可以在模型预测控制中实现。编写MATLAB程序，从而实现对转运车横向运动加速度进行预测控制。

3 仿真分析

将集装箱转运车的ADAMS模型导入到MATLAB/Simulink中进行联合仿真，联合仿真模型如图7所示。其中，“Adams_Vehicle”模块为导入到Simulink中的集装箱转运车的ADAMS模型，“MPC_contorl”模块为前文所述的模型预测控制算法在MATLAB中的实现，并由此得到的最优横向加速度作为联合仿真模型的输入，输出转运车的车身俯仰角及地面对前轮的支持力，对模型预测控制器进行验证。

图7 集装箱转运车横向运动联合仿真模型

Fig.7 Joint lateral motion simulation model of the LS-AGEV

模型预测控制程序中的参数设定如下：采样时间T=0.1 s；预测时域长度Np=20，控制时域长度Nc=4；约束边界为横向加速度ay，横向加速度增量Δay以及车身俯仰角φ的范围，根据前文得到的横向加速度与车身俯仰角的最大值，得到aymin=-1.3，aymax=1.3,φmin=-0.22,φmax=0.22；横向加速度增量Δay的限制会影响横向变化的快慢，选取|Δay|=0.1、0.12、0.08分别进行比较。另外，选取权重矩阵系数q=0.1,权重矩阵R=0.7；设置输出约束即期望的车身俯仰角为0。

将参考的横向运动加速度及车身俯仰角输入到模型预测控制器中，即可得到横向加速度的最优输入及其增量结果，从图9中可以看出，模型预测控制算法将输入的增量施加了限制，因此减缓了横向加速度输入的变化，从而得到最优输入如图8所示。而将此横向加速度输入到ADAMS模型中，得到车身俯仰角的变化以及前轮地面支持力仿真结果。从图10中可以看出相对于没有施加控制，通过模型预测控制算法得到的车身俯仰角的变化更为平缓，也可以满足俯仰角的几何约束，及车身俯仰角变化小于0.22 rad。通过分析其前轮附着力，如图11所示，可以看出通过控制，得到其前轮地面支持力在整个仿真过程中均保持大于0，不会出现倾覆的情况，满足运动学约束。

图8 横向加速度输入仿真结果

图9 横向加速度增量仿真结果

Fig.9 Simulation results with lateral acceleration increment

图10 车身俯仰角仿真结果

图11 前轮地面支持力仿真结果

比较不同横向加速度增量Δay的值，可以看出当将Δay限制在较小的范围(|Δay|=0.8)里集装箱转运车的俯仰角变化更为平缓，但是会导致横向加速度变化缓慢，从而降低了转运车横向运动的速度。相反，增加Δay的范围至0.12，从图10中可以看出，转运车的车身俯仰角变化较小，这是由于在这个限制下，通过程序得出的最优横向加速度输入有二次突变，从而减小了其俯仰角的变化，如图9所示；但是这样突然的加速度变化不易控制且会影响集装箱所承载的货物的安全性。而当横向加速度增量Δay限制在0.1时，集装箱转运车在提升了横向运行速度的同时，保持了车身俯仰角的相对平缓变化，且最大俯仰角也满足几何约束与运动学约束，因此，选取|Δay|为0.1可以使控制器得到更好的效果。

综上所述，利用模型预测控制，得到最优的横向加速度输入，很好地将车辆的俯仰角控制在约束要求以内，从而保证集装箱转运车在进行横向运动时保持稳定，不发生俯仰倾覆。另一方面，提升了转运车的速度，提高了转运车的灵活性，同时提升了港口运输的效率。

4 结论

本文是针对新型智能集装箱转运车的横向运动进行分析。由于集装箱转运车在横向运动时轴距短，质心高，所以在启动及制动时会因为惯性的原因发生前后俯仰，如果加速度过大，则会发生倾覆。为了避免这样的危险情况发生，运用模型预测控制方法，对转运车的横向运动进行控制。

模型预测控制算法的实施过程进行了推导，并对方法进行仿真，通过联合仿真结果可以看出通过该方法很好地限制了集装箱转运车在横向运动时的车身俯仰角，保证了车辆运行的稳定性，从而满足集装箱转运车的特殊工况的需求。