温度变化对桥梁静载试验结果的影响

■杨臻恺

（1.福建省交通科学技术研究所，福州 350004；2.福建省公路、水运工程重点实验室，福州 350004）

1 前言

自上个世纪80年代以来，随着国民经济的增长，我国公路桥梁建设进入一个快速发展阶段，预应力混凝土T梁桥如雨后春笋般随处可见。如何精确评估该类梁桥的真实承载能力关系到人民生命安全与财产问题。

近年来，桥梁静载试验已成为评定结构承载能力的最有效方法之一，其结果的准确性与否直接影响到策略的科学性与合理性。桥梁静载试验检测是一项系统性强、又严密的工作性质，其试验结果受多种因素制约。如文献［1-2］分析表明结构的离散化、边界约束条件模拟、材料参数和非结构构件是影响桥梁荷载试验的主要因素，其中混凝土弹性模量最显著，非结构构件次之，单元离散化和边界条件均较小；文献［3］以某空心板桥为工程依托，采用Midas Civil有限元软件分析了桥面铺装、护栏、支座约束等因素对结构校验系数的影响，结果表明没有考虑二期荷载得到的校验系数值偏低，支座约束条件对校验系数值影响可忽略。文献［4］分别从设计软件、计算简化、设计保守、桥梁自身缺陷等方面对校验系数值影响规律展开简要分析。

综上所述，目前学者对桥梁静载试验结果影响值可归为设计、有限元软件分析、有无考虑二期荷载三大类，而关于静载测试环境温度变化对结果值得影响规律研究分析尚少见报道。为此本文以西北某预应力混凝土梁桥为工程背景，分析桥梁静载试验前后不同温度差异值对结果值的影响规律，该研究可为桥梁承载力的正确评定提供参考与借鉴。

2 模型的建立

2.1 工程背景

某预应力混凝土连续T梁桥桥址位于西北地区，夏季昼夜平均温差值在18°左右。设计荷载等级为公路-Ⅰ级，上部桥型布置为75m=3×25m，全长81m，桥型纵向布置如图1所示。桥面总宽为11.0m，由5片T梁组合而成，每片T梁横向间距为2.1m，翼缘板中间湿接缝宽度为0.4m，T梁高度为2.30m，其中内梁预制宽度为1.80m，边梁预制宽度为2.05m。主梁、湿接缝、现浇连续段均采用C50砼；下部采用柱式墩，桥台采用柱式台及肋板台及钻孔灌注桩基础。

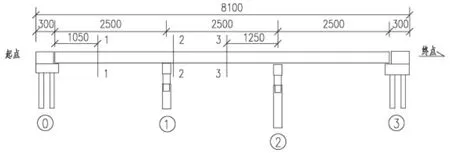
图1 桥型纵向布置图

2.2 有限元模型

采用Midas Civil软件建立有限元分析模型，上部主梁、横隔板、盖梁、桥墩等构件均采用梁单元模拟，桥面铺装层用板单元模拟。主梁与盖梁采用不同的弹簧刚度值模拟实际支座约束，墩底按固结方式模拟边界条件。加载试验车辆轴力等效为集中力分配到相应的位置处，C50混凝土弹性模量值取3.45×105N/mm2。三维有限元模型如图2所示。

图2 三维空间有限元模型

3 静载试验与分析

为了验证有限元数值模型可较为精确反映现场实测环境温度变化对结果值的影响，对实桥结构进行静载加载试验，并将结果值与理论值对比。

3.1 试验环境

依据《公路桥梁荷载试验规程》（JTG/T J21-01-2015）[5]规范3.3条试验环境要求，荷载试验应选在气温较为平稳时段，尽量避开高温、强光、强风、雨雪等恶劣环境对试验结果的影响。为了更为真实地测试结构承载能力，与当地气象部门取得联系，获取近期72h内的气温、风速变化规律等可靠天气预报资料，选择最佳稳定时段实施荷载试验。

3.2 测试项目

依据规范［5］要求，对投入运营的桥梁静载荷载试验效率 宜介于0.95～1.05之间，其中ηq的计算公式如式(1)：

式中：Ss为静载试验下控制截面内力计算值；S为控制荷载下截面最不利内力值；μ为冲击系数。根据图1桥型结构受力特点，拟选取1-1、2-2-、3-3三个截面进行偏载（最不利工况）试验分析，分别测试每片T梁在荷载作用下的应力（应变）以及扰度值。

3.3 测点布置

分别在各个截面梁底布设应变片测试点，依照1-1、2-2、3-3 截面从右向左测点编号分别为 A1～A5、B1～B5、C1～C5，截面应变测点布置见图3。

挠度测点主要布置在1-1、3-3截面对应每片T梁顶面铺装位置处，以检测每片T梁在车辆荷载作用下的扰度值，对应测点编号分别是 A1’～A5’、C1’～C5’，跨中扰度测点布置如图4所示。

3.4 测试结果对比分析

为了使有限元数值分析结果更能反应实际测量值，拟加载的车辆荷载尽可能使每片T梁试验效率ηq均在1.00上下波动。通过多次有限元静载加载试验数值对比分析，最终采用2辆总重均为34.5t的三轴车加载。在最佳试验温度环境下（试验前后温差变化仅为0.5°），控制截面位置处对应T梁梁底的应变、扰度与实测值对比结果如表1～2所示。

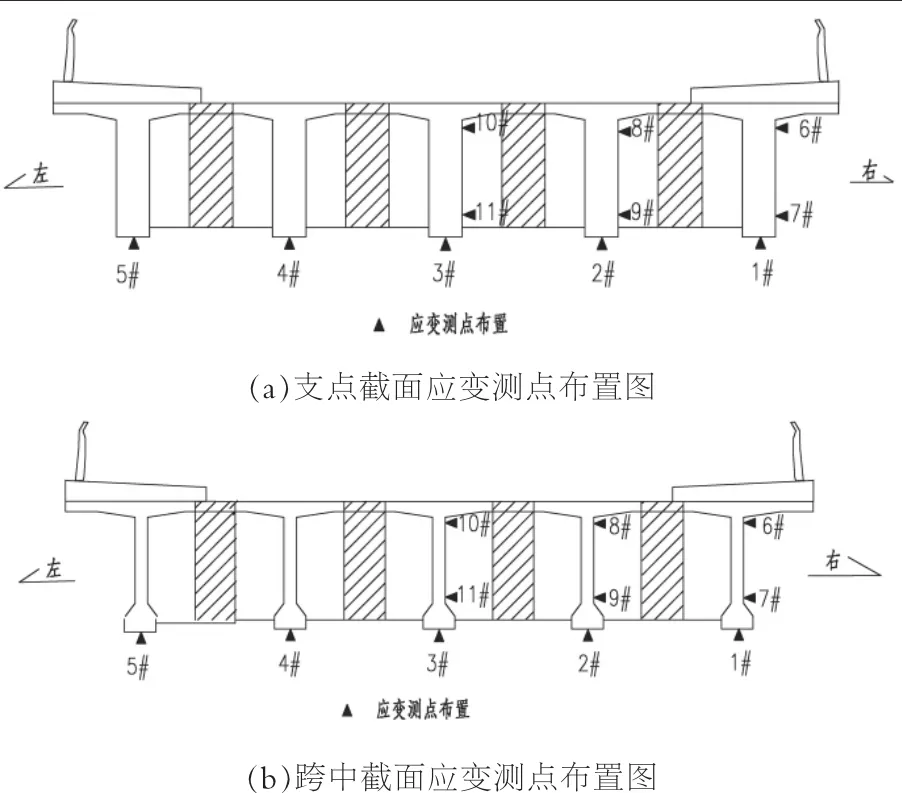
图3 应变测点布置图

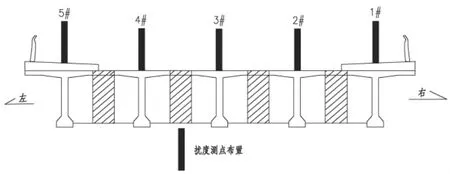
图4 跨中截面扰度测点布置图

由表1～2可知，在相对较为稳定温度环境下，不论是控制截面的应变值还是扰度值与有限元分析结果误差值均小于2.5%，符合工程要求精度。验证了该桥有限元数值模型建立、分析的准确性与可靠性，理论分析值可真实反映结构工作状况。

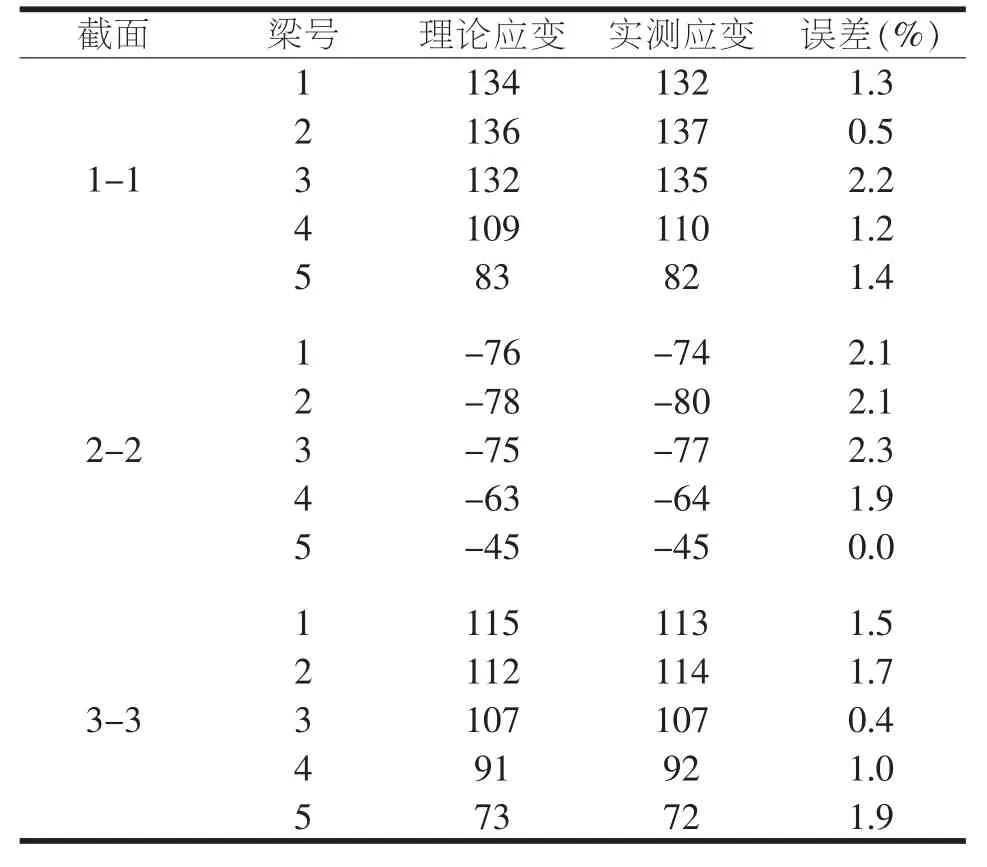
表1 各截面应变或应力变化对比值

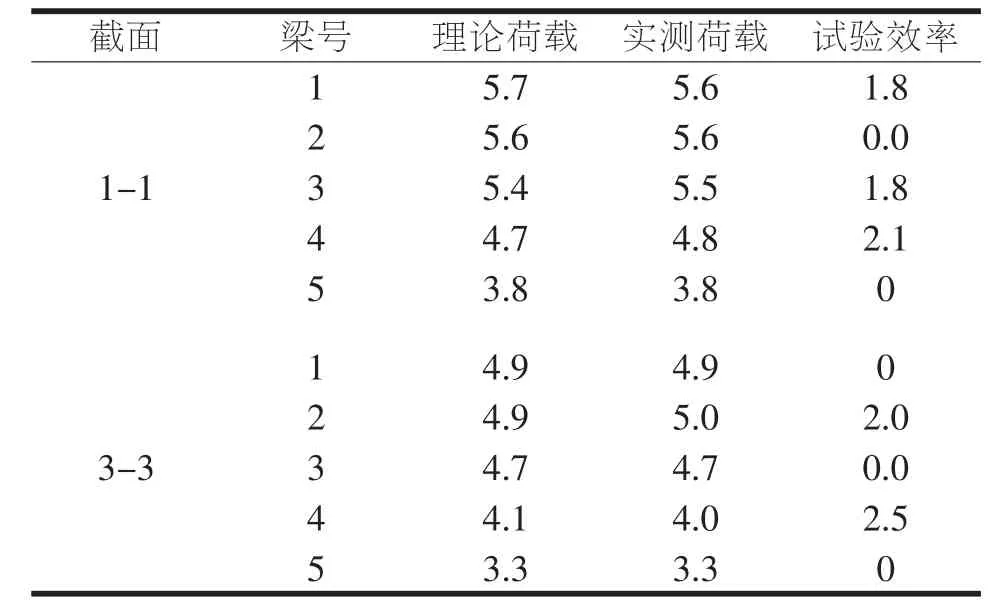
表2 控制截面处的应变/扰度相对残余值

4 温度变化

由上一节有限元数值分析与现场实测数据值对比结果可知，采用Midas Civil软件模拟分析静载试验环境温度变化对结构承载能力的影响方式是可行的。分别设置了温度差为 2°、4°、6°、8°和 10°的五种工况。 在不同的温差工况下，各个控制截面位置处的每片T梁应变、扰度值与真实值误差详见表3～4，数值变化曲线图如图5～9所示。

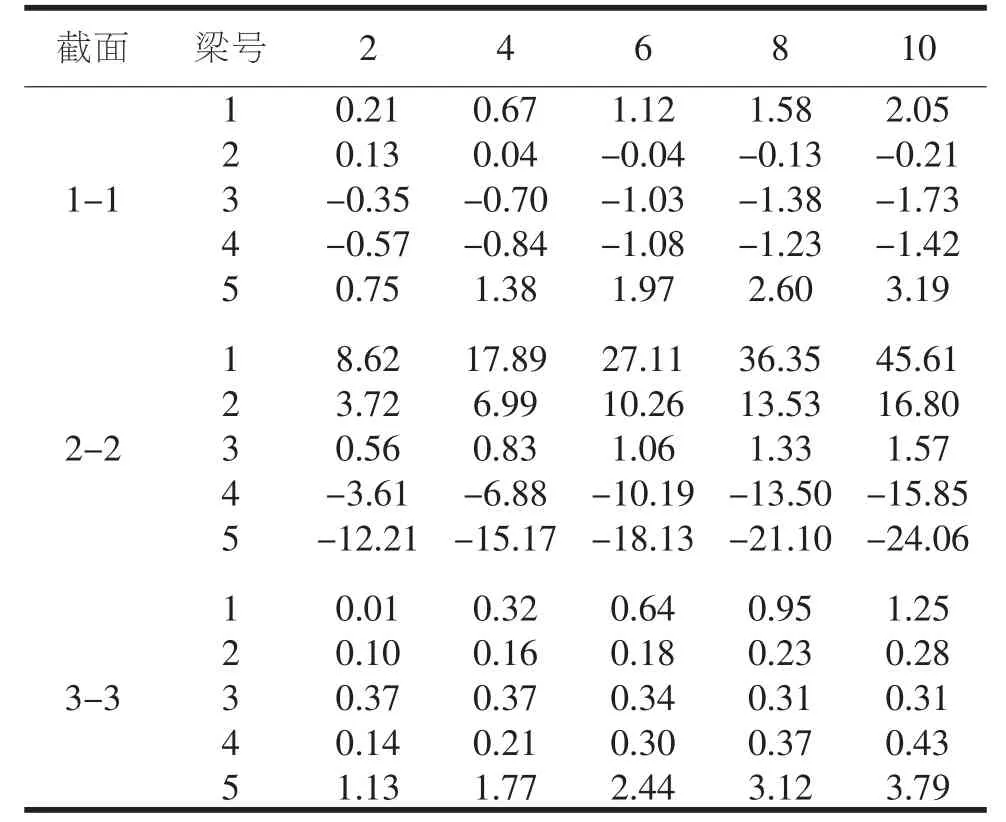
表3 不同温差工况下控制截面的应变误差值（%）

表4 不同温差工况下控制截面的扰度误差值（%）

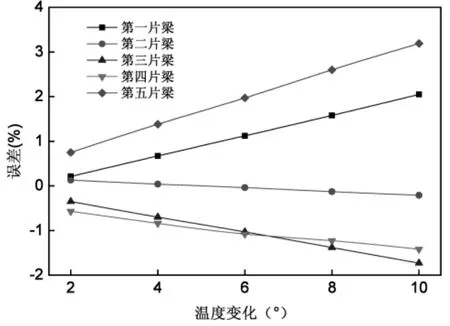
图5 不同温差工况下1-1截面应变误差值变化曲线图

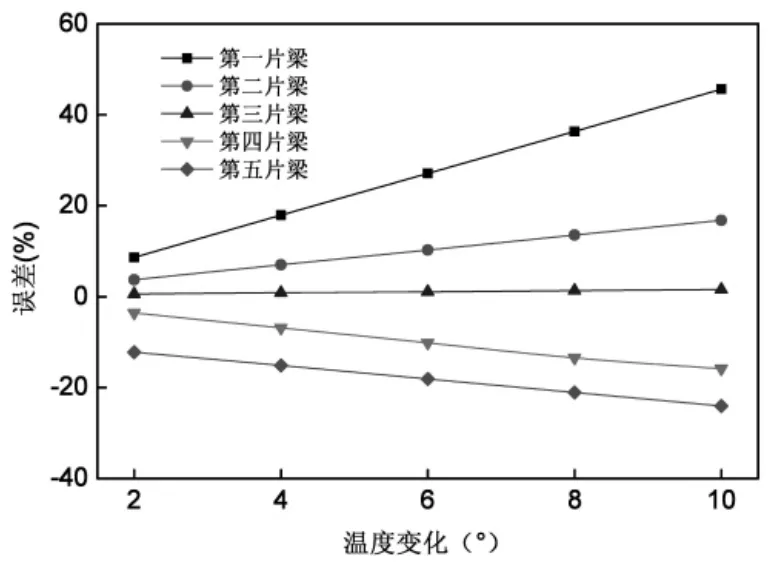
图6 不同温差工况下2-2截面应变误差值变化曲线图

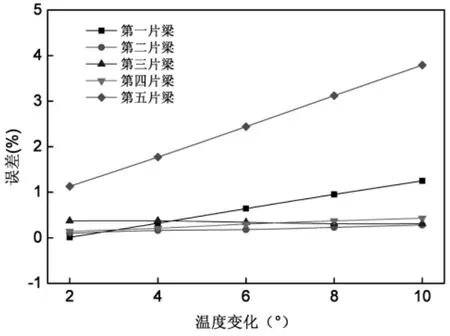
图7 不同温差工况下3-3截面应变误差值变化曲线图

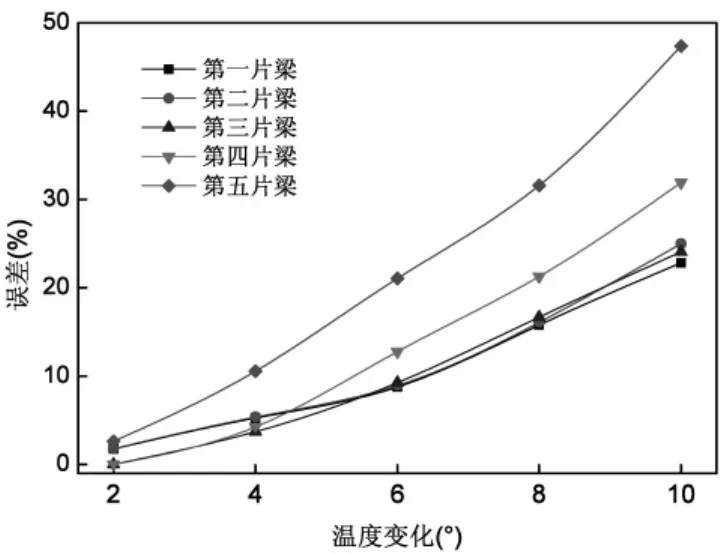
图8 不同温差工况下1-1截面扰度值误差变化曲线图

图9 不同温差工况下3-3截面扰度误差变化曲线图

从表3及图5～图7可知，随着环境温度差从0°增大到10°时，各个控制截面的应变误差值近似呈线性变化规律，随着温差的增大，误差值也越大。其中1-1和3-3截面测点应变误差值受温度差变化影响较小，最大值仅为3.79%；而2-2截面应变误差值受其影响尤为敏感，当温差在10°工况时，1#T梁的应变误差值高达45.61%。

从表4及图8～图9可知，各个控制截面的扰度测点误差值均随着检测环境温度差值的增大而增大。且不同的截面位置误差值影响幅值差异较大，当静载试验环境温差从2°增大到10°时，边跨1-1截面处的最大扰度误差值达到了47.37%，而中跨3-3截面最大误差值仅为6.06%。

由上述温差变化影响规律分析可知，不同的截面位置处的应变、扰度误差值受静载试验环境温度变化敏感性均有所不同，1-1截面扰度值和2-2截面应变值受温差变化尤其显著，其主要是因为支点梁、墩处采用固定支座连接，一方面温度变化产生的梁体次内力较难释放，导致2-2截面梁单元内力急剧增大，另一方面边梁纵向自由伸缩，不受支座纵向约束，使得边跨扰度误差值增大较为显著。

5 结论

总体上桥梁结构静载试验的应变、扰度误差值均随着环境温差值的增大而增大；且不同截面处的应变、扰度误差值受温差变化影响幅值差异较大，尤其是支点负弯矩截面处的应变值和边跨最大弯矩截面处的扰度值，均随着温差值的增大而急剧增大，其余截面对应的内力值受测试环境温度变化影响较小。建议实际桥梁结构静载试验时，应尽量选择在温度较为稳定时段，能够更为精确地评定实际结构承载能力。