高速冷轧机辊系非线性动力学模型及控制参数优化

王桥医 朱 媛 过 山 张秋波

杭州电子科技大学机械工程学院，杭州，310018

0 引言

轧机振动是影响高速冷轧机轧制质量和生产效率的重要影响因素之一［1－2］。轧机振动，尤其是垂直振动［3－5］会使带钢厚度不均、波痕明显，降低带钢产品质量，限制轧制速度，加速轧辊磨损，甚至破坏轧机设备，造成巨大的财产损失［6－7］。随着轧制设备技术和控制水平的提高，轧机表现出的“幽灵式”耦合振动［8］成为世界范围内困扰钢铁业的重大难题。目前，国内外学者分别从轧机结构和轧制过程的非线性因素两种角度对轧机振动做了大量研究。刘晓潺等［9］建立了多方向耦合振动下的连轧机再生振颤模型并验证其正确性；刘浩然等［10］研究了轧机结构刚度的分段非线性特性引起的振动；侯东晓等［11］、刘彬等［12］考虑轧机振动位移变化的影响，推导出动态轧制力的表达式；NIROOMAND等［13］基于波传播理论研究了张力在机架间的变化以及张力变化对轧机振动的影响；XU等［14］引入动态摩擦方程，研究了非稳态润滑情况下轧机的垂直振动特性并验证其正确性。但是，轧机振动是轧机结构因素和轧制过程因素相互耦合导致的一种自激振动［15］，目前结合这两种非线性因素的研究较少，因此，建立相关的耦合动力学模型进行深入研究显得很有必要。

本文借鉴相关的非线性力学模型，综合运用轧制过程动态轧制力模型、轧机系统分段非线性弹性力模型和分段非线性摩擦力模型，建立了考虑非线性因素耦合的高速冷轧机辊系动力学模型，采用平均法［16］求解幅频响应方程，研究了轧机系统主要参数对轧机垂直振动的影响。

1 轧制过程动态轧制力模型

轧机高速轧制时，轧制变形区不仅包括塑性区，而且包括出入口弹性区。本文考虑带钢在轧制过程中发生的弹性变形、塑性变形、轧辊压扁半径和垂直振动位移的影响，建立了轧制过程力学模型（图1）。图1中，d1、d2分别表示稳态轧制时轧件的入口厚度和出口厚度，d表示轧辊发生颤振时轧件的动态出口厚度，v1表示轧件入口速度，σ1表示轧件入口张力，σ2表示轧件出口张力，vr表示上工作辊和下工作辊的转动线速度，转动方向相反，R表示工作辊半径，R′表示考虑工作辊压下量的轧辊半径，y1、y2分别表示上辊系和下辊系的垂直振动位移，以向下为正方向。侯东晓等［11］据图1提出了动态轧制力变化量表达式：

式中，P2为动态轧制力变化量；y为振动位移；P 为稳态轧制力。

图1 轧制过程力学模型Fig.1 Mechanical model of rolling process

式（1）、式（2）体现了轧制过程中轧制力的变化规律，描述了弹塑性变形阶段轧制力与振动位移的关系，体现了轧制变形过程中的轧制力的非线性。

2 分段非线性约束力学模型

轧机振动主要表现为机架与轧机辊系间的相对运动，主要受到许多非线性参数的影响。当轧机辊系处于高载荷、高速度运转的工作状态时，压下缸和弯辊缸非线性弹性力和非线性摩擦力的微小变化也会使轧机系统失去平衡，故不可忽略其大小。为了研究的全面性，本文考虑振动位移的所有情况，分段表示轧机辊系受到的非线性弹性力和非线性摩擦力。

2.1 分段非线性弹性力模型

非线性弹性力表现为等效线性刚度上叠加等效非线性刚度的微量，其表达式为

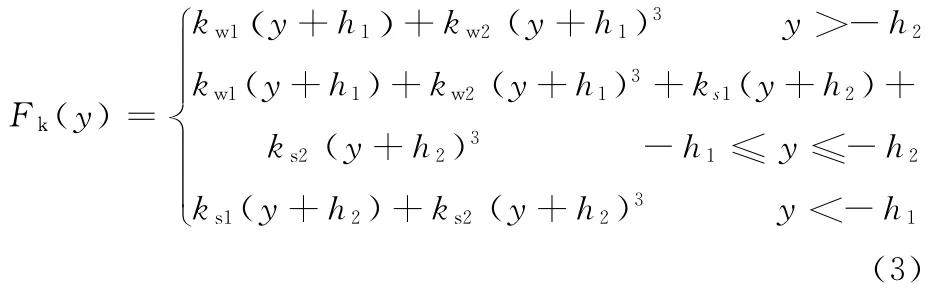
式中，ks1、kw1分别为压下缸和弯辊缸的等效线性刚度；ks2、kw2分别为压下缸和弯辊缸的等效非线性刚度；h1、h2分别为稳态轧制时压下缸和弯辊缸在预压力作用下的弹性变形量，h1＞0，h2＜0。

2.2 分段非线性摩擦力模型

由于压下缸和弯辊缸活塞杆与缸壁间的摩擦因数不是常量，随振动速度的变化而变化，故摩擦力呈非线性。摩擦因数表达式为

式中，μ为摩擦因数；μs为静摩擦因数；μm为最大动摩擦因数；vm为最大振动速度。

非线性摩擦力分段表达式具体如下：

式中，p为压力，其大小与密封件装配松紧程度、密封件材料材质硬度、跟随性、强度、载荷径向分量等因素有关；y′为振动速度，当y′＝0时，液压缸缸壁和活塞间摩擦力为静摩擦力，大小为外扰力P1。

3 轧机辊系动力学模型

将上述轧制过程动态轧制力、非线性弹性力和非线性摩擦力这三种非线性因素进行耦合，构成高速冷轧机辊系的动力学模型，具体耦合关系如图2所示。

图2 力耦合关系图Fig.2 Coupling relations of forces

本文将轧机系统中的元件简化为集中的质量、弹簧和阻尼，构成常用的简化“弹簧－质量－阻尼”模型。考虑四辊高速冷轧机结构对称，建立考虑非线性因素耦合的轧机辊系动力学模型，如图3所示。图3中，m表示上工作辊、上支承辊及轴承座的等效质量，k1、c1分别表示上辊系与机架上横梁的等效刚度和等效阻尼，k0、c0分别表示轧件等效刚度和等效阻尼。由图3列出动力学方程如下：

图3 轧机辊系动力学模型Fig.3 Dynamic model of roll system

式（6）两边同除以m，化简得

F′ky（）和P′2的表达式为

式中，α、β为非线性弹性力的非线性项系数；γ为非线性摩擦力的非线性项系数。

4 轧机辊系系统响应的确定

采用平均法，设轧机受到周期性外扰力P′1＝P0sinωt，ω2＝ω01＋εσ（），其中，σ为调谐因子，ε为小参数。当ε充分小时，ε越小，系统运动越接近周期运动。则式（7）可表示为

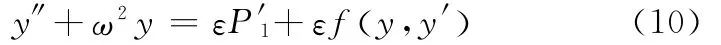
其中，非线性项

则可推导得出a和θ的微分方程，具体表达式如下：

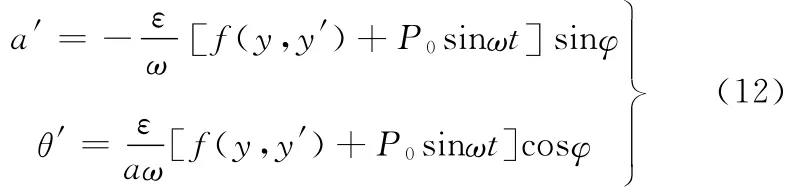
将式（12）等号右边的项用一个周期（－π，π）内的平均值近似替代，可得平均化方程，具体表达式如下：

为了研究的全面性，考虑轧机振动幅值分段的3种情况，即a＞max（｜h1｜，｜h2｜），则式（13）分段积分结果具体表达式如下：

式（14）中N1、N2的具体表达式如下：

令a′＝0，θ′＝0，消去式（14）中的θ，求得系统幅频响应方程：

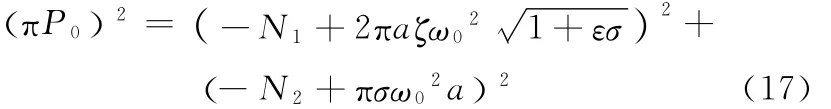
由式（17）可以看出，动态轧制力一次项刚度B1、三次项刚度B3、非线性弹性力非线性项系数α和β、非线性摩擦力非线性项系数γ、外扰力幅值P0和线性阻尼ζ对于抑制非线性因素耦合下的高速冷轧机辊系的垂直振动起着十分重要的作用。

5 结果与分析

根据建立的考虑非线性因素耦合的高速冷轧机辊系动力学模型及其系统响应，以某企业2800单机架四辊高速冷轧机工艺参数和实际生产数据为例，对轧机系统进行数值仿真分析，主要研究轧机系统主要参数对轧机振动特性的影响。四辊冷轧机的轧制主要参数见表1。

表1 四辊冷轧机轧制参数Tab.1 Parameters of four-high cold rolling mill

轧机系统非线性参数项、外扰力和线性阻尼为定值时，轧机系统的振动幅频特性与动态轧制力一次项刚度和三次项刚度的关系见图4和图5。图4中，动态轧制力一次项刚度B1对轧机振动固有频率有较大影响，在固有频率处，轧机系统存在跳跃现象。随着B1的减小，幅频曲线沿横坐标向右移动，轧机系统振动固有频率增大，振幅减小。因此，合理改变一次项刚度B1的大小可以有效地抑制轧机振动现象。

图4 动态轧制力一次项刚度变化时系统振动幅频曲线Fig.4 The vibration amptitude frequency curve of the rolling system as the primary stiffness of dynamic rolling force changes

如图5所示，动态轧制力三次项刚度B3对轧机系统振动影响很大，随着B3的减小，轧机系统的幅频响应曲线沿横坐标逐渐向右移动，固有频率增大。B3为0时，振动幅值最大且不存在跳跃现象，此时系统的解唯一且稳定。B3不为0时，轧机系统振幅变化不明显，但出现明显的跳跃现象，系统易失稳。如图5中曲线4所示，频率沿横坐标正向变化时，系统幅值沿A-B-C-E的路径变化，在C-E 处幅值迅速减小，系统振荡明显。频率沿横坐标负向变化时，系统幅值沿E-D-B-A的路径变化，在D-B 处系统幅值剧增，系统失稳。

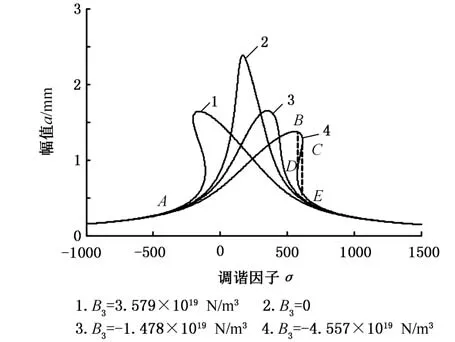
图5 动态轧制力三次项刚度变化时系统幅频曲线Fig.5 The vibration amptitude frequency curve of the rolling system as the cubic stiffness of dynamic rolling force changes

如图6所示，α和β越大，非线性弹性力越大，振动幅值越小。α和β较小时，无跳跃现象，轧机系统的解唯一且稳定。当α和β足够大即非线性弹性力起主导作用时，轧机系统易出现跳跃现象，此时轧机系统在正常生产过程中极易失稳。

图6 非线性项系数α、β变化时系统幅频曲线Fig.6 The vibration amptitude frequency curve of the rolling system as the nonlinear coefficientsα、βchanges

如图7所示，对比α、β、γ的取值可知，非线性摩擦力对轧机系统振动的影响比非线性弹性力敏感。γ增大，轧机系统振动幅值明显减小，且轧机系统跳跃现象减弱，非线性摩擦力的分段特性对振动的影响也由此减弱。此时，非线性摩擦力在轧机系统中表现出阻尼特性。因此，合理增大γ可起到抑制轧机系统振动的作用。

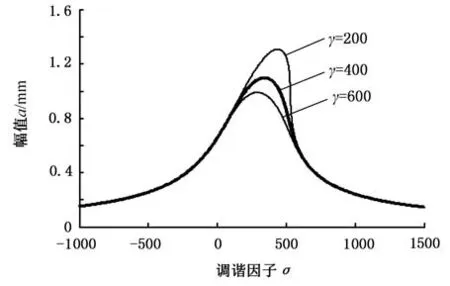
图7 非线性项系数γ变化时系统幅频曲线Fig.7 The vibration amptitude frequency curve of the rolling system as the nonlinear coefficientsγchanges

如图8所示，随着外扰力幅值P0增大，轧机系统振动幅值增大，共振越激烈。P0值变化时，轧机系统固有频率几乎无变化，轧机系统共振点不存在跳跃现象，因此，可以适当减小外扰力幅值来实现系统控制参数优化，从而抑制轧机系统振动现象，提高系统稳定性。

图8 外扰力P0变化时系统幅频曲线Fig.8 The vibration amptitude frequency curve of the rolling system as extraneous force P0changes

由图9和图10可知，线性阻尼ζ对轧机系统振动幅值和固有频率影响较小。随着线性阻尼的增加，振动幅值略有减小，轧机系统出现跳跃现象，轧机系统发生振荡。对比线性阻尼ζ的取值和幅值变化可知：线性阻尼值越大，轧机系统振动幅值减小越缓慢。

6 结论

（1）本文考虑轧制过程动态轧制力、轧机系统分段非线性弹性力和分段非线性摩擦力的共同作用，建立了高速冷轧机辊系非线性因素耦合的动力学模型，利用平均法求出幅频响应方程，分析了主要参数对轧机系统振动的影响。

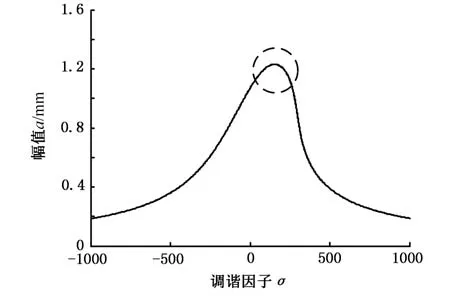
图9 线性阻尼ζ变化时系统幅频曲线Fig.9 The vibration amptitude frequency curve of the rolling system as linear dampingζchanges

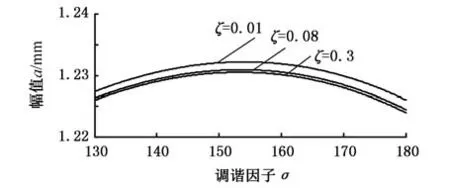
图10 线性阻尼ζ变化时系统幅频曲线局部放大图Fig.10 The local amplification of vibration amptitude frequency curve of the rolling system as linear dampingζchanges

（2）动态轧制力一次和三次项刚度对轧机系统非线性有直接影响。一次项刚度越小，轧机系统振幅越小，固有频率越大；三次项刚度不为零时跳跃现象明显，极易失稳；三次项刚度为零时，振动幅值最大。

（3）非线性弹性力越大，振动幅值越小；非线性弹性力起主导作用时，发生跳跃现象且易失稳；非线性摩擦力越大，轧机系统振动幅值越小，跳跃现象越不明显，分段特性越弱。因此，在一定范围内增大分段非线性约束，可削弱分段特性的影响且能抑制轧机振动。

（4）外扰力幅值越大，则振动幅值越大，共振越剧烈；线性阻尼值越大，轧机振动幅值越小且减小越缓慢。因此，选取较小的外扰力和适当增加线性阻尼，可有效地控制系统振动。