基于马柯威茨模型的投资组合最优化实证研究

李悦莹 何传敏

（中南民族大学数学与统计学学院，湖北 武汉 430074）

引言

如今，中国经济正在高速发展，国家各族人民的生活水平有了很大提高，特别是在中国加入世界经济贸易组织之后。金融和经济都在向全球化发展。越来越多的中国人过上了富裕的生活，他们的家庭也有自己的积蓄。其中，投资股票等证券占投资比例的大部分，投资的目的是获得比银行无风险投资状态更高的回报。但是投资是有风险的，高收益伴随着高风险。

一、马柯威茨模型

假设K同时投资了n个证券组合，每一种证券的投资权重分别是x1,x2……,xn，第i种证券的权重是xi。则向量x=(x1,x2,…,xn)T是投资权重的向量，引入一个n维单位向量e，则e=(1,1,…,1)n，所以有：

对于K 投资的各种证券，其回报率不确定，因此可以用ri表示第i种证券的收率。E（ri）表示第i种证券收益率的期望，则这n种证券期望收益率的向量为（E（r1）,E（r2）,…,E（rn））T,为了方便阅读书写令μi=E(ri),(i=1,2,3,…,n)，所以收益率的向量就可以写成μ=(μ1,μ2,…,μn)T。

马柯威茨认为方差就是投资收益水平的不确定性因素可以用来描述风险，前文所说的两个目标即为期望收益率之和E和方差σ2，所以可以建立如下模型：

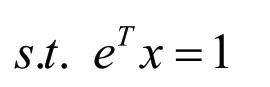
二、模型实证

根据2015年12月份20只股票的月收益率，本文随机抽取4只股票:中国联通、龙净环保、同仁堂、贵州茅台，由收益率求出这四只股票的协方差矩阵W,假设K是一位稳建地投资者，偏好系数α，β，λ分别为0.3；0.2；0.5，最低收益率是无风险利率，以中国银行2015年一年定期存款利率为标准，令r0=3，因此：

即为：μ=（3.47,4.31,5.88,1.95）T，投资权重：

之后转化为无约束问题：

得到最终解：

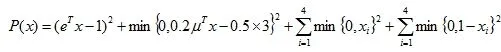
三、结论

证券投资优化模型是在股票型基金债券进行商业投资过程中最大化投资收益的数学模型。虽然计算过程比较复杂，但本文通过对实际问题的解决方案表明，组合投资数学模型对于实际市场是可行的。在考虑最小回报的基础上，为投资者进行证券投资管理提供了良好的管理方法。这对真正的证券投资市场来说非常实用。