一种适用于火星气动捕获的自适应预测制导算法*

唐青原，王晓磊

0 引 言

火星作为我国深空探测的下一阶段主要目标，也是人类最有可能展开大规模探测的大行星，其轨道捕获制动所需的速度增量超过2 km/s，燃料消耗占比很高，这一问题在未来的采样返回或载人任务中显得尤为突出.因此，如何在火星轨道捕获环节节省燃料的同时实现准确安全入轨成为了火星探测的关键问题之一.相较于传统化学燃料脉冲变轨，气动捕获技术在节省燃料方面具有相当大的优势.早期的研究[1]中就对气动捕获制导与控制精度和轨道特性进行了分析，认为利用气动辅助实现轨道捕获是可行的，并且设计高升阻比气动参数可以做到变轨精度与脉冲变轨精度在同一数量级.马歇尔航天飞行中心在文献[2]中对气动捕获和纯推力制动两种方式的优缺点进行了研究，在对携带4台890 N轨道机动发动机的地球返回舱进行模拟分析后，得出结论：纯推力制动、一次性大气制动需要的发动机开机时间分别是51 min和6 min，相当于节省了88%的燃料.文献[3]则就不同的应用场景论述了气动捕获制动在节省燃料方面的优势.

关于气动捕获技术的研究始于20世纪80年代[4]，通常是指使探测器接近段双曲线轨道进入天体大气中，通过倾侧角的变化合理利用气动力，使探测器在飞出大气后进入目标环绕轨道.早期的气动捕获制导律[5]是在阿波罗进入制导律[6]的基础上演变而来的一种解析制导律.但纯解析制导很难满足精度和鲁棒性的要求，因此后续发展出了以阻力平面跟踪[7]为代表的混合预测校正制导，该方法使探测器姿态在一定阶段跟踪某一阻力平面，而后以一恒定的下降速率飞出大气.近些年，因为具有较高的制导精度以及较强鲁棒性，数值预测校正制导成为了解决气动捕获问题的常见方法[8].其中文献[9]为了提高控制能力，在控制量中加入了攻角，不过在工程实践中攻角控制还存在实现难度.

不同于已经成功实施了4次的气动减速技术，气动捕获技术依然处于研究和地面试验阶段.这主要是因为依靠单次气动减速实现捕获需要的速度增量远远大于气动减速单圈的速度增量，使得飞行风险大大提高；而火星大气稀薄，大气密度不确定性强，伴有偶发性全球风暴.并且轨道射入任务本身关系着整个任务的成败，一旦失败更是没有补救措施，因而对于气动捕获任务而言，重中之重是制导方法具有较强的鲁棒性以适应环境不确定性和初始条件的不确定性，使得探测器在极限工况下也能安全入轨.

因此本文提出一种结合了数值预测校正和高度跟踪解析制导的分段气动捕获制导算法，其中数值预测校正部分应用通过动态输入增益变换的全系数自适应控制算法，以退出大气后的远拱点高度为控制目标，以求实现精确入轨；而高度跟踪制导则保证飞行器的主减速段轨道高度不会过低的同时下降速率也几乎为0，弥补了全系数自适应算法所缺少的边界条件控制.最后对标称条件下及各类极限工况下该制导律的表现进行了仿真验证，结果表明，气动捕获制动可以有效地减少燃料消耗，该制导算法具有较强的鲁棒性，可以在各类极限工况下实现准确安全入轨.

1 气动捕获问题的建立

1.1 动力学模型

旋转大气模型下探测器大气内飞行的三自由度动力学方程为：

(1)

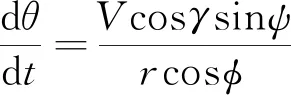
(2)

(3)

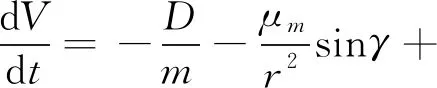
(4)

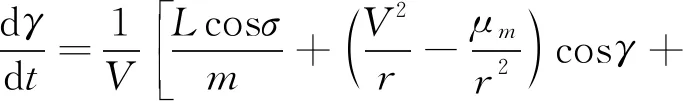
2ωmVsinψcosφ+

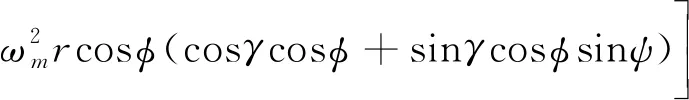
(5)

2ωmV(cosφtanγcosψ-sinφ)+

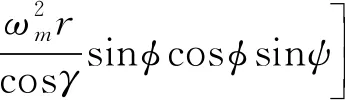
(6)

其中，r为火星中心距，θ和φ为经纬度，V为速度大小，γ为飞行路径角，进入大气时的该角度又称为进入角，ψ为航向角，此处指北为0，ωm为火星自转角速度，σ为倾侧角，L和D为升力和阻力，其表达式如下:

(7)

其中，ρ为火星大气密度，S为飞行器的气动参考面积，CL、CD分别为升力系数和阻力系数.

实际上在进行制导律设计时可简化使用非旋转的大气模型，令式(1)～(6)中ωm=0,这样就实现而来飞行状态方程纵横向解耦，如下式所示：

纵向运动方程：

(8)

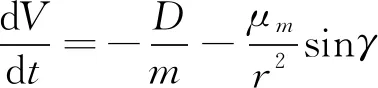
(9)

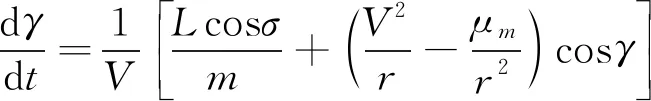
(10)

横向运动方程：

(11)

(12)

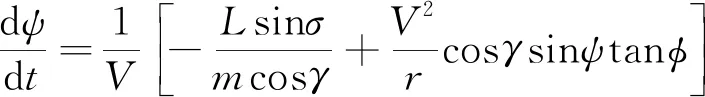
(13)

在纵横向解耦的前提下可以对纵横向轨迹分开进行设计.其中纵向运动方程只和倾侧角σ的大小有关，和符号无关，主要影响的是轨道的形状和大小，是控制律设计的关键；而横向运动方程还受到倾侧角σ的符号影响，横向运动主要影响的是轨道平面，即角动量的方向.

1.2 大气模型

火星大气密度ρ的不确定度很大，现阶段人类对火星大气的了解有限，大气模型的建立主要基于不同的大气数据库，比较常用的有NASA建立的一系列火星全球大气数据库和欧空局建立的欧洲火星气候数据库，二者都是给定飞行器的经纬度、轨道高度以及时间，可得到包括大气密度在内的一系列数据.但这种方式对于星上自主轨道控制系统来说过于复杂，并且大气模型本身也不够成熟，因此设计制导律时通常使用简化的数学模型.常用的大气模型是指数模型，其最为简洁的形式如下[10]：

ρ=ρ0e-h/hs

(14)

式中,h为探测器轨道高度，ρ0=1.474×107kg/km2为火星大气参考密度，hs=8.8057 km为火星大气比例高度.

式(14)描述的大气模型仅与轨道高度有关，而实际上，同一高度不同纬度，大气密度不一致，时间不同，同一轨道高度上的大气密度也会发生变化，故有如下更为精确的密度模型[11]：

(15)

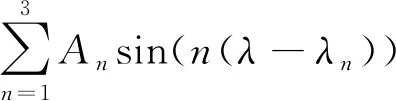
1.3 控制目标及评价标准

由双曲线轨道到椭圆环绕轨道的气动捕获问题，根据控制目标可分为目标远拱点控制和能量最优控制.若令rexit、Vexit、γexit分别表示探测器退出大气后轨道半径、速度和飞行路径角，则目标远拱点控制可表示为：

(16)

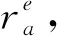
(17)

(18)

探测器由双曲线轨道经气动捕获制动最终入轨目标停泊轨道的过程如图1所示.探测器飞出大气后，椭圆轨道近拱点位于大气内，需要在远拱点进行轨道机动抬升近点高度，需要速度增量ΔV1;当探测器再次飞至近拱点时，还需要再次进行轨道机动，调整远拱点控制误差，需要速度增量为ΔV2.因此能量最优控制的目标是使ΔV2最小或者|ΔV1|+|ΔV2|最小.

图1 气动捕获过程示意图Fig.1 Overall approach of aerocapture

以上两种控制目标的气动捕获问题的最终评价标准都是飞出大气后进行的轨道平面内机动所需的速度增量.从双曲线到椭圆轨道变化过程中，探测器轨道的远拱点变化范围可以达到数千公里，范围极大；相比而言由于退出大气后的轨道近点一定在大气内，即大概在10～130 km范围内，较远拱点的变化范围小很多.同样的误差率，发生在远拱点造成的绝对误差远远大于在近拱点造成的误差，此外近点抬升制动是不可避免的，优化空间不大，而远拱点若将控制精度提高到一定程度，理论上可以避免远拱点调整制动.因此在考虑控制目标时，优先考虑远拱点控制精度.相应地，评价气动捕获效果的速度增量也分为抬升近拱点速度增量ΔV1和总速度增量|ΔV1|+|ΔV2|.

(19)

|ΔV1|+|ΔV2|=

(20)

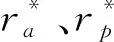
2 制导方法

气动捕获预测校正制导的一般思想是，不断计算以当前倾侧角飞行时，出大气后轨道与目标轨道的误差来产生倾侧角增量控制指令，再根据新的飞行状态预报出大气后轨道参数新的误差，如此往复，直到满足控制需求为止.具体到本文，控制量是倾侧角序列，输出量是预报的出大气后终端轨道远拱点半径误差，控制系统框图如图2所示.

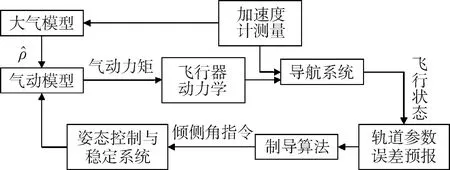
图2 气动捕获制导系统框图Fig.2 System flowchart of aerocapture guidance system

如1.1节所述，设计制导律时三自由度动力学模型通过简化实现纵横向解耦后，分别进行制导律设计.其中纵向运动方程只受倾侧角大小影响，纵向制导律中的控制量仅大小变化；横向制导律同时受倾侧角大小和符号影响，可使用倾侧角翻转策略，使得横向速度分量逐步收敛.本节将设计完整的探测器气动飞行制导律，以同时实现轨道的形状和轨道面控制.

2.1 纵向制导律

一般认为火星大气接口在火星平均表面150 km高空处，大于150 km的高空可近似认为没有气动力作用，此时气动加速度大约为10-9数量级，气动力作用很有限.随着轨道高度降低，火星大气密度将大幅升高，而较低层高密度大气的不确定性也大大降低，因此中低层大气是用于实现降低轨道能量的主要轨道段.

本文所使用的全系数自适应算法属于一种数值预测校正模型，通过不断预测当前输入下轨道的远拱点半径和目标远拱点半径的误差，反馈产生控制指令.该方法是通过建立单输入单输出间的一阶特征模型关系，实时估计参数，从而求取控制修正量的.文献[12]中通过将特征模型看作一种特殊的线性时变系统来证明稳定性，进而证明了该算法的收敛性，即保证了远拱点制导误差的收敛性.但这种方法无法保证轨道最大下降速率、最大过载、热流密度等多约束条件；此外该方法的目的是提高Δra的制导精度，但要进一步提高1.3节中所述的评价标注|ΔV1|+|ΔV2|,还需要进一步设计.

根据以上对制导算法和火星大气密度特性的分析，可以考虑将整个气动捕获任务分成不同的子任务段，分别用不同的制导律进行控制，具体如下.

(1)捕获过渡段

捕获过渡段是从飞行器进入大气开始，控制飞行器到达一个目标轨道高度结束.这一阶段的目的是使飞行器的轨道高度降低到下一阶段需要的特定巡航高度，因此采用预测校正算法.

首先对轨道高度误差hm相对倾侧角控制量σc做泰勒展开有：

(21)

保留一阶项，可得控制律：

(22)

其中：

(23)

Δσp是用于预测的一个倾侧角增量，hf1、hf2是依次预测的轨道高度误差.

hm1=hf1-hcruise

(24)

hcruise即为预设的巡航高度.

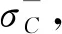
(25)

(2)平衡滑翔段

当探测器轨道降低到一定高度后，气动力矩作用开始显著，大气密度不确定性也较低，此时适用于利用气动力降低轨道能量保证形成环绕，同时也是需要考虑多约束条件主要阶段.

气动捕获问题的多约束条件主要包括最大过载、最大热流密度，以及保证安全飞行的最低轨道高度，具体表达式为：

(26)

(27)

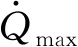
通过优化巡航高度hcruise等参数，还可以在后续阶段保证远拱点入轨精度的基础上进一步优化总体燃料消耗量，关于参数优化问题将在2.3节具体讨论.

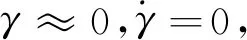
(28)

为跟踪巡航高度，制导律为

(29)

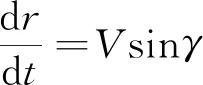
将制导律代入有

(30)

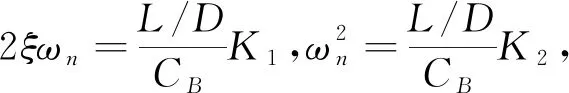
(3)逸出大气段

针对地球返回制导问题，胡军提出的全系数自适应预测校正制导算法[13]已经得到了在轨验证.和地球返回再入任务类似，火星气动捕获任务也是一类大气辅助变轨任务，且在纵向通道控制律设计过程中都可以简化为单一量的控制目标.因此本文借鉴载人飞船全系数自适应再入升力控制的方法，将全系数自适应控制理论首次引入气动捕获预测校正算法领域.

全系数自适应控制理论的原理是：系统一般能用n阶定常差分方程来近似描述，若允许差分方程的系数是时变的，则可将系统看作一个小于n阶的变系数模型，其建立的基础是全系数之和等于1[14]，或接近于1.因此，不同于传统预测校正算法，每个制导周期内，自适应算法不需要进行迭代求控制量，而是根据输入输出关系辨识出系统此刻的输入输出关系，再根据线性反馈或黄金分割控制等方法得到控制量.这种方法一方面避免了在每个制导周期内多次进行递推预测，大大提高了计算效率；另一方面该方法根据系统误差反馈，每个周期不断根据新的预测信息修正制导控制量，逐渐逼近控制目标，属于闭环无差系统.系统初始误差和制导过程中产生的误差一起均匀分布在整个制导过程中，因此可以期望得到较高的鲁棒性.

本文的制导系统中输入为远拱点制导误差，输出为倾侧角变化，二者数量级差异巨大，要保证系数之和等于1，需要进行输入变化.而倾侧角ΔσC对最终远拱点误差的影响是一个和时间有关的函数，若对当前气动飞行的飞行器施加一个倾侧角增量ΔσC,其纵向分量将产生如下变化：

cosσ=cosσ0+a×1(t)

(31)

计算ΔσC的作用时长tapply对远点半径误差的影响曲线，当a=0.1时仿真打点结果如图3所示.

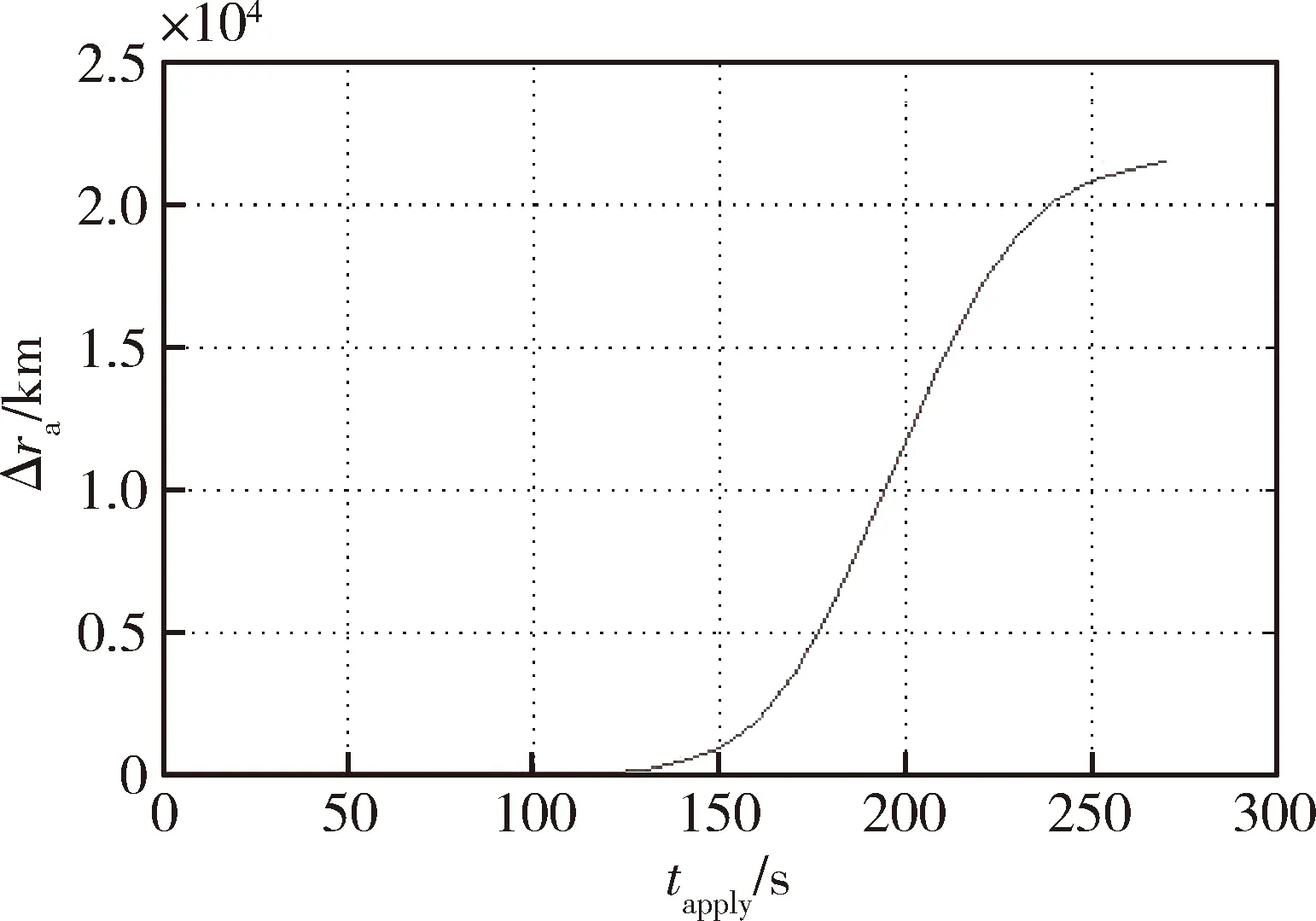
图3 ΔσC的作用时长对远点半径误差的影响曲线Fig.3 The increment of apoapsis range caused by the applying duration of ΔσC

图中的纵轴是当前轨道预报得到的远拱点半径和倾侧角全程为0°时的远拱点半径间的误差；横轴是ΔσC的作用时长.可以看出，ΔσC的作用时间越长，对远拱点误差的影响越大，且中间低轨道大气稠密段加入时产生的影响变化较大.

定性地来说可将这一曲线看作a×1(t)的变化到远拱点半径误差的时变放大倍数.将其作为控制系统的输入变换，使得变换后的系统放大倍数保持在1附近，可期望保证全系数之和近似为1.

定义1.t时刻施加倾侧角变化量Δσ(t)后，预测的远拱点制导误差产生的变化量定义为动态输入增益A(t).

为了减少在线进行预测的计算量，文献[13]中将图3曲线拟合成关于作用时间的多项式函数，但在气动捕获问题里该曲线幅值变化范围过大，且前后高空大气段变化微弱，中段变化极快，难以用简单函数描述.因此，本文采用事先生成标称情形下的动态输入增益数据集A0，在线根据Δσc作用时间插值的方法生成输入变换系数.

根据以上分析，可利用全系数自适应控制方法进行制导律设计.这一阶段的控制目标是瞄准目标轨道远点半径，则退出大气后环绕轨道的远点半径制导误差为：

(32)

则当前时刻制导系统的输入为：

(33)

利用一阶特征模型建立系统输入输出间关系：

y(k)=ΦT(k)θ(k)+e(k)

(34)

式中,ΦT(k)=[y(k-1)u(k-1)]T，u(k-1)表示上一时刻倾侧角的余弦值cosσ(k-1).

被估参数向量θ(k)=[a1(k)β0(k)]T

需保证a1(k)+β0(k)→1

参数估计公式为

θ(k)=θ(k-1)+

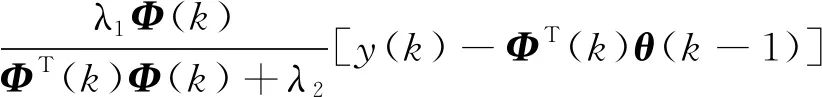
(35)

线性反馈控制uL(k)=-l1a1(k)y(k)/β0(k)

每次产生的控制量uL(k)是倾侧角余弦的修正量Δcosσ(k),还需通过积分器产生新的倾侧角.该方法不需要事先规划标称轨道，并且每个计算周期只进行参数估计，而不用迭代求取控制量，结合上述动态增益的离线化处理，可有效减少在线计算量.

2.2 侧向制导律

如前所述，气动飞行的侧向通道控制可以使用倾侧角符号反转的方式，只要设置翻转阈值，在符号的不断变换过程中侧向速度将逐渐收敛.以下是其中一种侧向通道制导方式.

设初始轨道面单位法向矢量：

(36)

侧向速度：

vlat=v·I0

(37)

制导律：若vlat≥vthr则倾侧角符号翻转，vthr即为设定的侧向速度阈值.由于侧向速度逐渐收敛，该速度阈值也应逐次减小.

2.3 参数优化

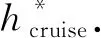
求取|ΔV1|+|ΔV2|的方法选择文献[15]中一种改进的Golden-Section的方法，这种方法结合了Golden-Section和连续抛物线插值，在保证计算收敛的同时考虑到了收敛的快速性.而进一步考虑在轨计算量，参数确定的思路可分为离线优化和在线辨识两部分.

2.3.1 离线优化

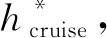
2.3.2 在线辨识

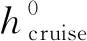
仿真表明，各个极限工况下巡航高度主要取决于初始轨道特性，在轨运行中的不确定性对其影响不大，因此hcruise的优化问题可采用离线标称环境下的结果；而退出巡航速度vd在不同的非标称环境下表现较为敏感，对最终总速度增量的影响也较大，因此选择在线优化.

2.3.3 气动参数辨识

气动捕获问题中的不确定性分为大气环境不确定性和气动参数不确定性，根据气动力公式，这两类不确定性可以折算到升力和阻力两个量中.在轨可以利用加速度计测量当前轴加速度，表达式为：

(38)

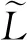
(39)

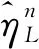
(40)

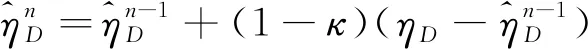
(41)

其中κ∈(0,1),是滤波常数.

3 仿真校验

3.1 研究对象

引言中提到气动捕获的两种应用场景：采样返回和载人任务，前者特指无人采样探测任务.无人任务和载人任务的探测器在气动外形、边界约束条件和任务周期等方面有着很大的不同.本文的研究对象为前者，即无人采样返回探测任务，因此探测器构型假定为低升阻比的钝头体.因没有已在轨实施的项目，无人气动捕获任务的相关研究较少，因此本文的气动参数选择基于2 500 kg这个质量规模，主要参考已进行过气动减速任务的火星环球勘探者型号，并比较了几个已有的试验项目的气动参数，从中进行选择，得出以下气动参数的航天器作为研究对象.

表1 气动参数初值Tab.1 Aerodynamic parameters of design reference

根据无人任务进行最低能量转移，进入火星影响球后相对火星的轨道速度，适度放宽得到研究的进入点速度，并根据无控时该速度对应的进入走廊γentry∈[-10.8°,-9.5°],选定进入轨道倾角，因而有如下进入点轨道初始条件及目标椭圆轨道.

表2 进入点轨道初值及控制目标Tab.2 The initial orbit at the Mars atmosphere interface and the target orbit

作为参考，该初始和目标轨道，若应用传统脉冲点火进行平面内变轨，所需的速度增量约为2 077 m/s，根据利亚普诺夫方程，当采用推力为1 500 N，比冲为310 m/s的发动机制动，所消耗的燃料质量约为1 238 kg.

3.2 仿真结果

为直观起见，以下仿真结果除图4外将分为横向和纵向制导展示，为了给横向制导提供控制裕度，倾侧角幅值的变化范围为(15°,165°).图4显示的是本文描述的制导算法下倾侧角的变化序列.轨道预测的频率是1 Hz，考虑到实际工程中有角速度转动上限，10 s改变一次倾侧角.初始的大气作用很小，在气动加速度和引力加速度之比小于0.05时，不做制导，最后的逸出段一直进行到理论上的大气层边界处，此处为表明大气边界，将倾侧角置0.

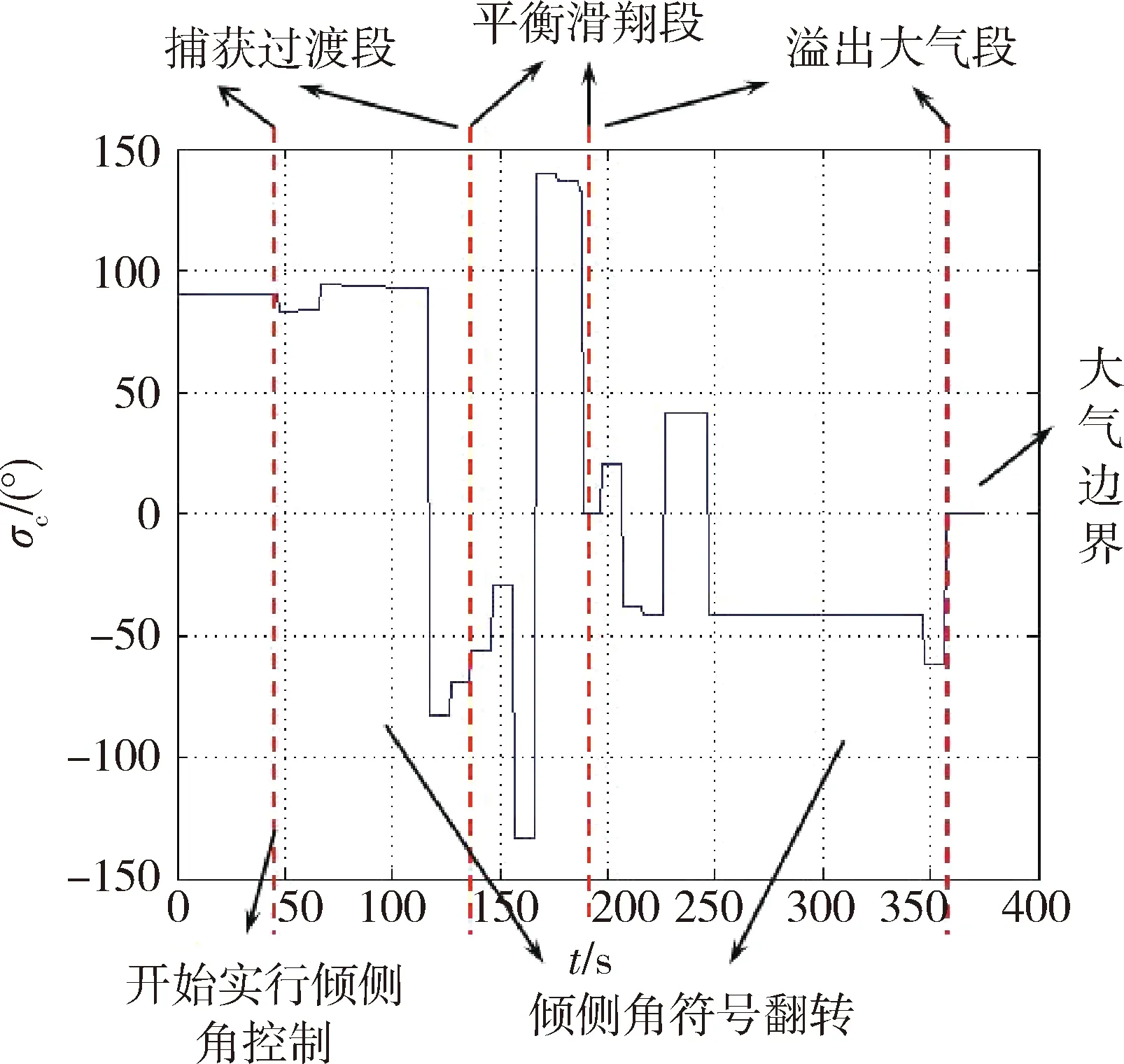
图4 纵横向耦合倾侧角变化序列Fig.4 The bank angle profiles of longitude and lateral coupled movements

3.2.1 横向制导

侧向速度的变化规律如图5所示，红色折线标记出横向速度边界，该边界随不同制导阶段逐步缩小，达到使得横向速度收敛的目的，有略微超出的部分就是10 s改变一次倾侧角导致的超调.仿真结果显示，侧向速度收敛后，最终轨道倾角的控制精度在0.03°以内.

3.2.2 纵向制导

如表3所示，本文选取了5种极限工况情形，包括，大气密度幅值拉偏、大气密度波、气动升力系数和阻力系数拉偏.其中气动系数相关的拉偏对应探测器气动参数这一初始条件的不确定性，大气密度相关拉偏对应环境不确定性，多次仿真取均值后标称情形(编号0)和各个极限工况下的制导结果如表3所示.初始条件不确定性还包括进入大气时的初始轨道不确定性，图6中给出了多种极限工况下不同初始进入角对应的制导结果Monte Carlo图.

文献[16]中提出了一种基于庞德里亚金极大值原理的两段式数值预测校正气动捕获制导算法，该方法同时考虑了远拱点控制精度和速度增量优化，比较具有代表性.其校正环节通过二分法和三次插值法迭代寻找使得Δra=0的控制量.表4中对上述数值预测矫正法(NPC)和本文提出的全系数自适应制导法(ACA)在极限工况下进行了仿真对比.

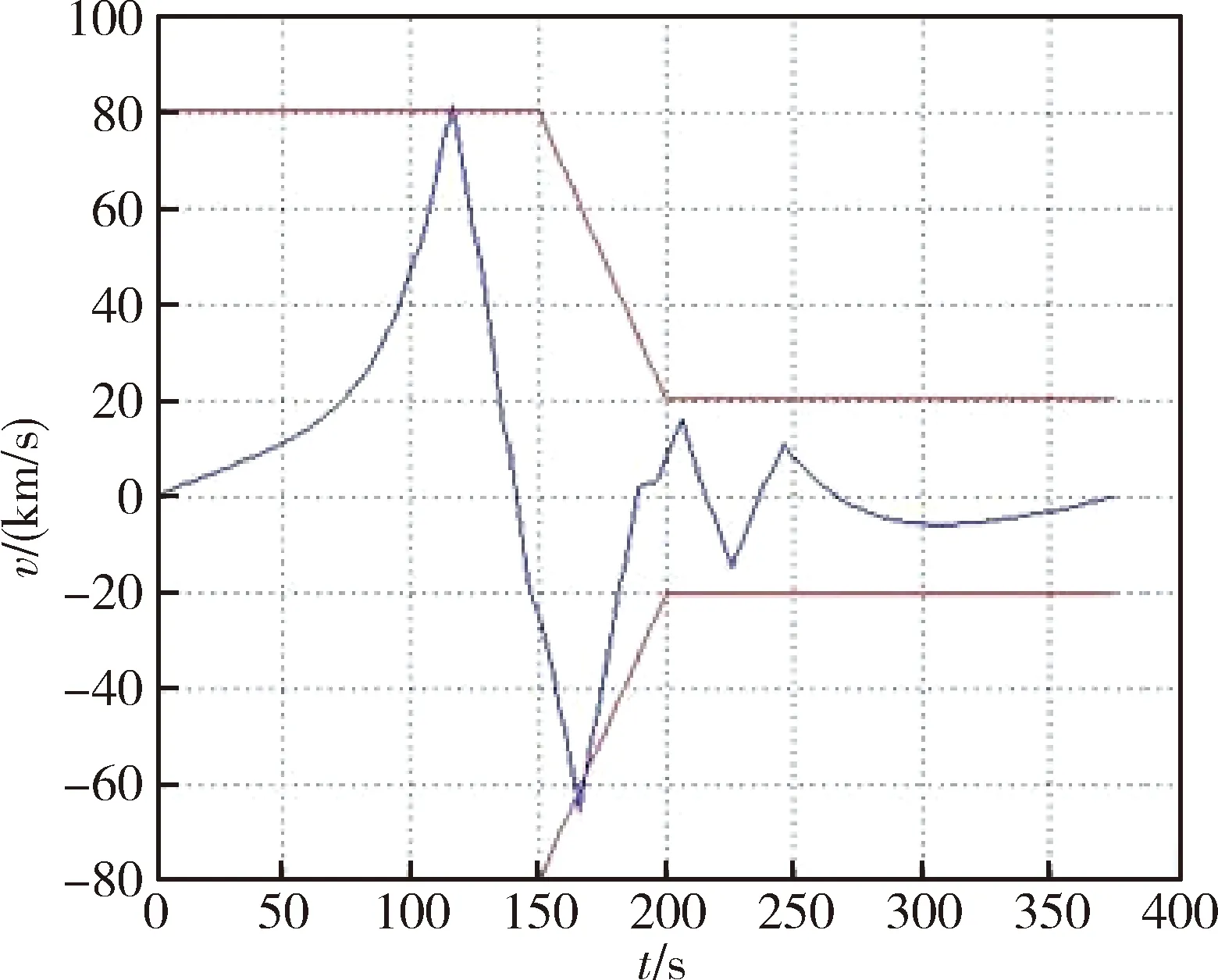
图5 横向速度变化曲线Fig.5 The lateral velocity curve

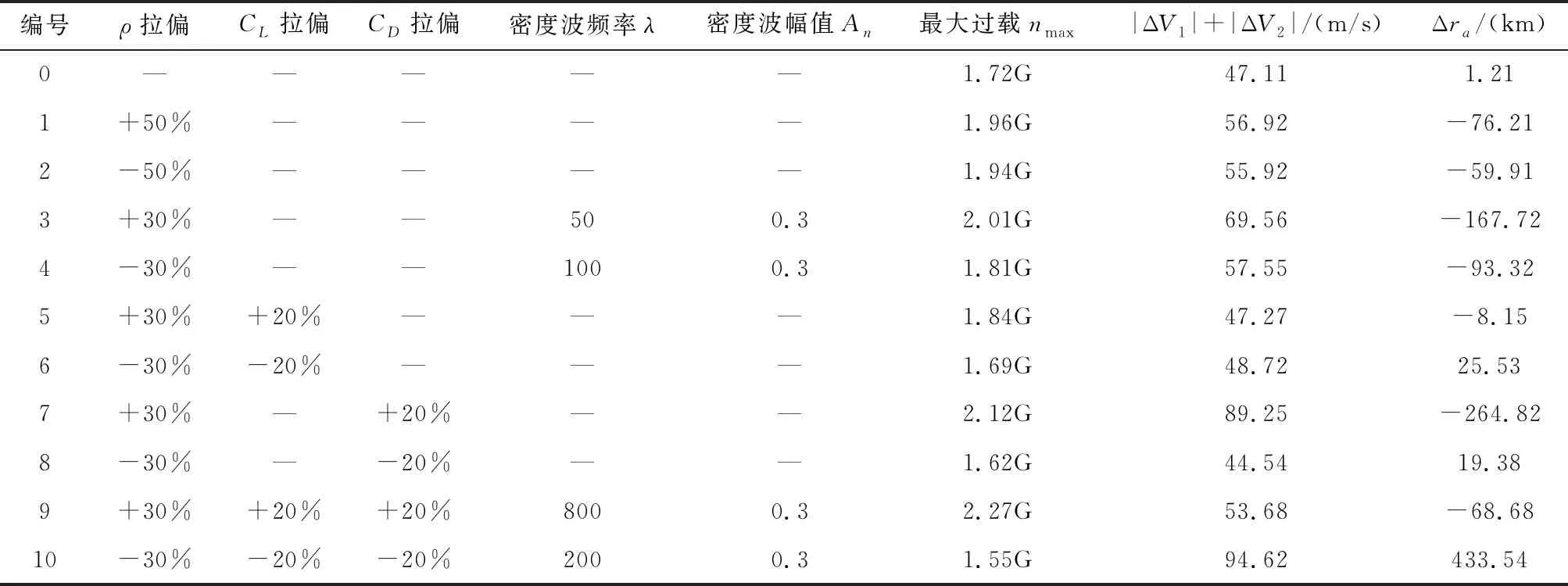
表3 多种极限工况组合下制导仿真结果Tab.3 The simulation results of multi off-nominal conditions

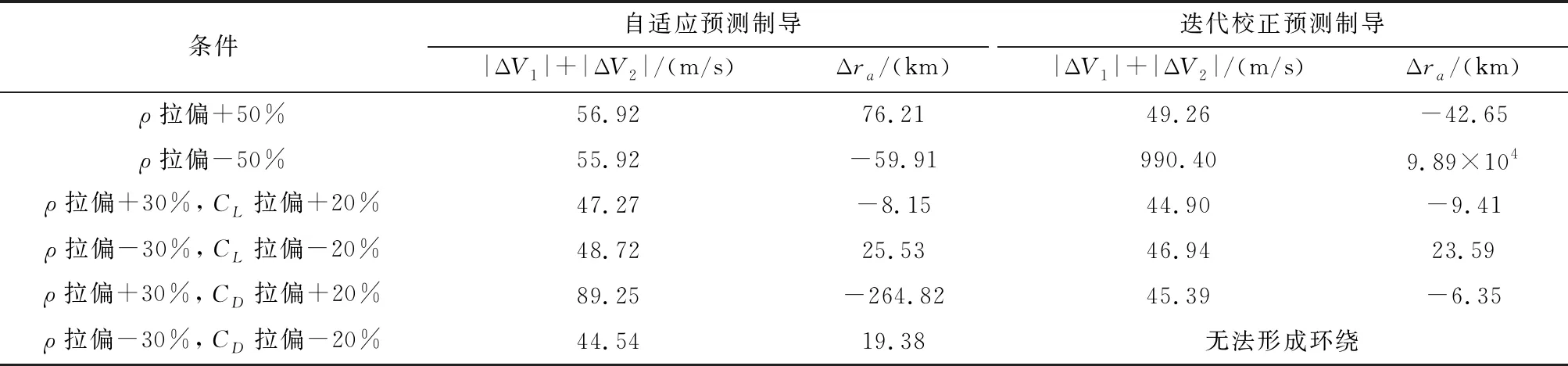
表4 极限工况下制导算法结果对比Tab.4 The simulation results of multi off-nominal conditions between ACA and NPC method

表3中可以看出，对制导结果影响较大的非标称情形是高频率密度波和大气密度大幅度正向拉偏，即情形3和1.升力系数和阻力系数的误差影响主要取决于最终造成的升阻比的误差.例如情形7和9中都对阻力系数进行了+20%的拉偏，但9中即便还加入了低频密度波影响，因为也同时加入了+20%的升力系数拉偏，使得整个升阻比变化不大，最后制导精度远远高于7中结果.情形10中大气密度和飞行器本身气动能力同时大幅下降，造成最终没有足够的气动力使得飞行器降低到目标远拱点高度.

结合表4数据，两种方法对远拱点的控制都可以达到较高精度.当大气密度偏高或升阻比较小时，数值预测校正法制导精度相对较高，但当大气密度偏低或升阻比偏大时，该方法的制导误差会大幅提高，当大气密度和阻力系数同时偏小时甚至无法成功形成环绕.而本文提出的方法表现与数值校正法正相反，大气密度偏低或升阻比偏高时制导精度较高，并且因为加入了一定的总速度增量优化策略，不论远拱点误差如何变化，后续平面内变轨所需的速度增量基本保持在了100 m/s以内，和脉冲点火制动相比减少了95%的能量需求，若考虑到有限推力产生的重力损耗，这一优势还将进一步扩大.

图6显示了不同初始进入角下本文提出的全系数自适应制导法(ACA)和数值预测矫正法(NPC)的制导结果对比.图中y轴为气动捕获后进入目标轨道所需的总速度增量ΔV=|ΔV1|+|ΔV2|.在一定的初始进入角范围内([-10.8°,-9.8°])数值预测校正法制导精度表现较稳定，但超出这个初始进入角范围后制导精度急剧下降，甚至无法形成环绕，气动走廊基本与无控情形下相同.而本文提出的基于全系数自适应控制理论的制导算法(ACA)在图中x轴所示的初始进入角范围内制导精度都基本相同.事实上，当γentry∈[-40°,-2.5°]时该方法都能得到较高的制导精度，极大地提升了进入走廊范围.

图7～10显示的是50次蒙特卡洛仿真的结果.可以看出，在各个极限工况的作用下，气动轨道特性基本相似，远拱点误差收敛较快.极限工况下大部分情形巡航段都可以跟踪0°飞行路径角，个别情形即使无法保持严格保持0°，也对最终轨道控制精度及评价标准没有明显影响.

图11显示的是气动捕获期间一阶特征模型两个时变参数的变化规律.可以看出两个参数之和保持了接近于1这个标准.

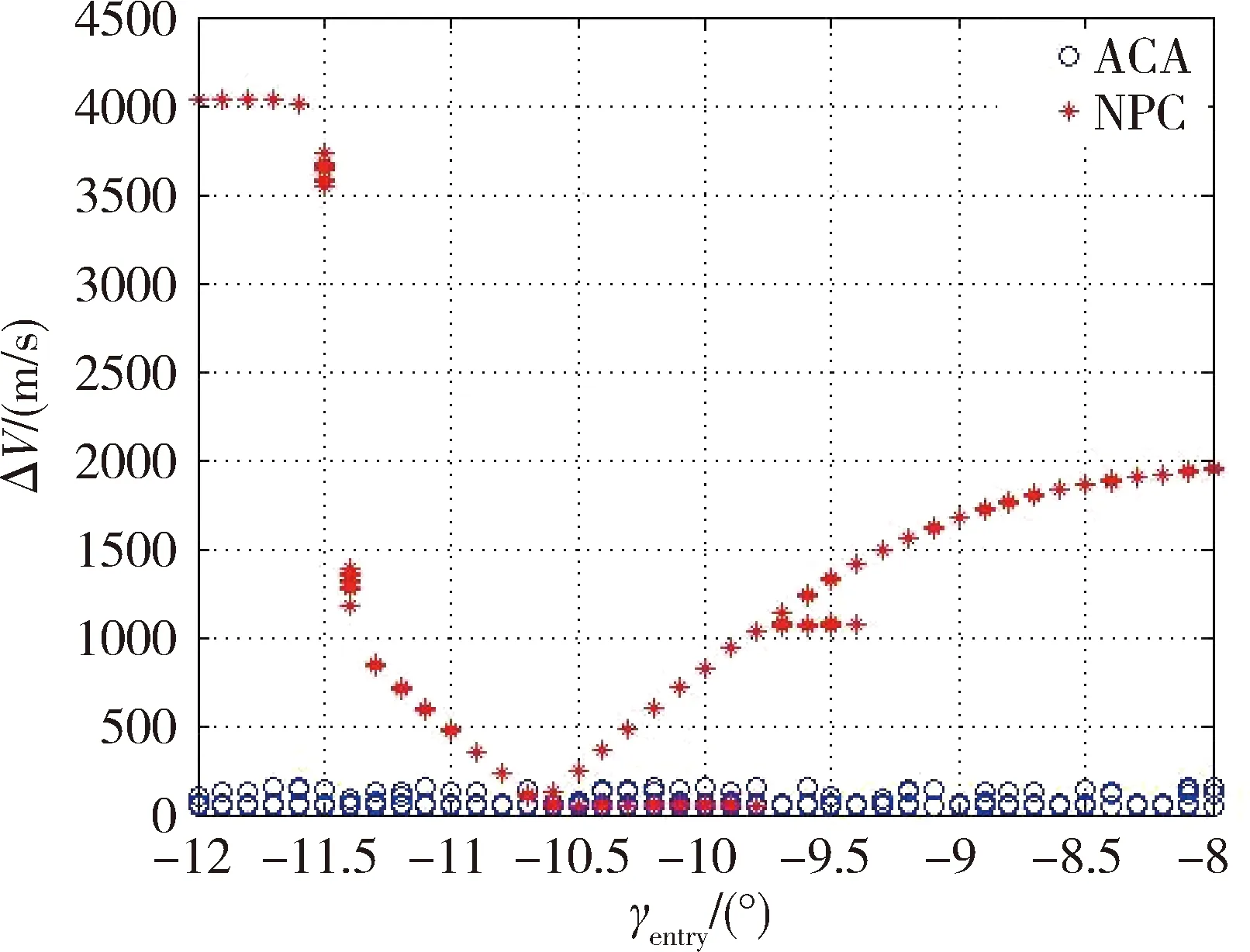
图6 不同初始进入角下两种算法的制导结果Fig.6 The guidance results with initial entry angle dispersion under two guidance methods

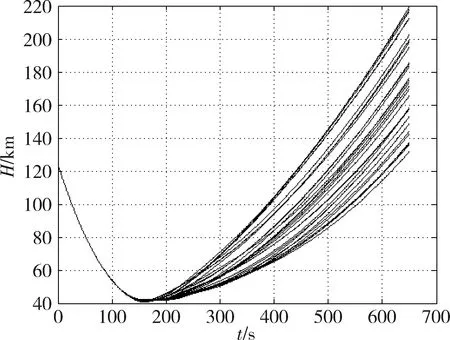
图7 轨道高度变化曲线Fig.7 Orbit height histories resulting from multi off-nominal conditions

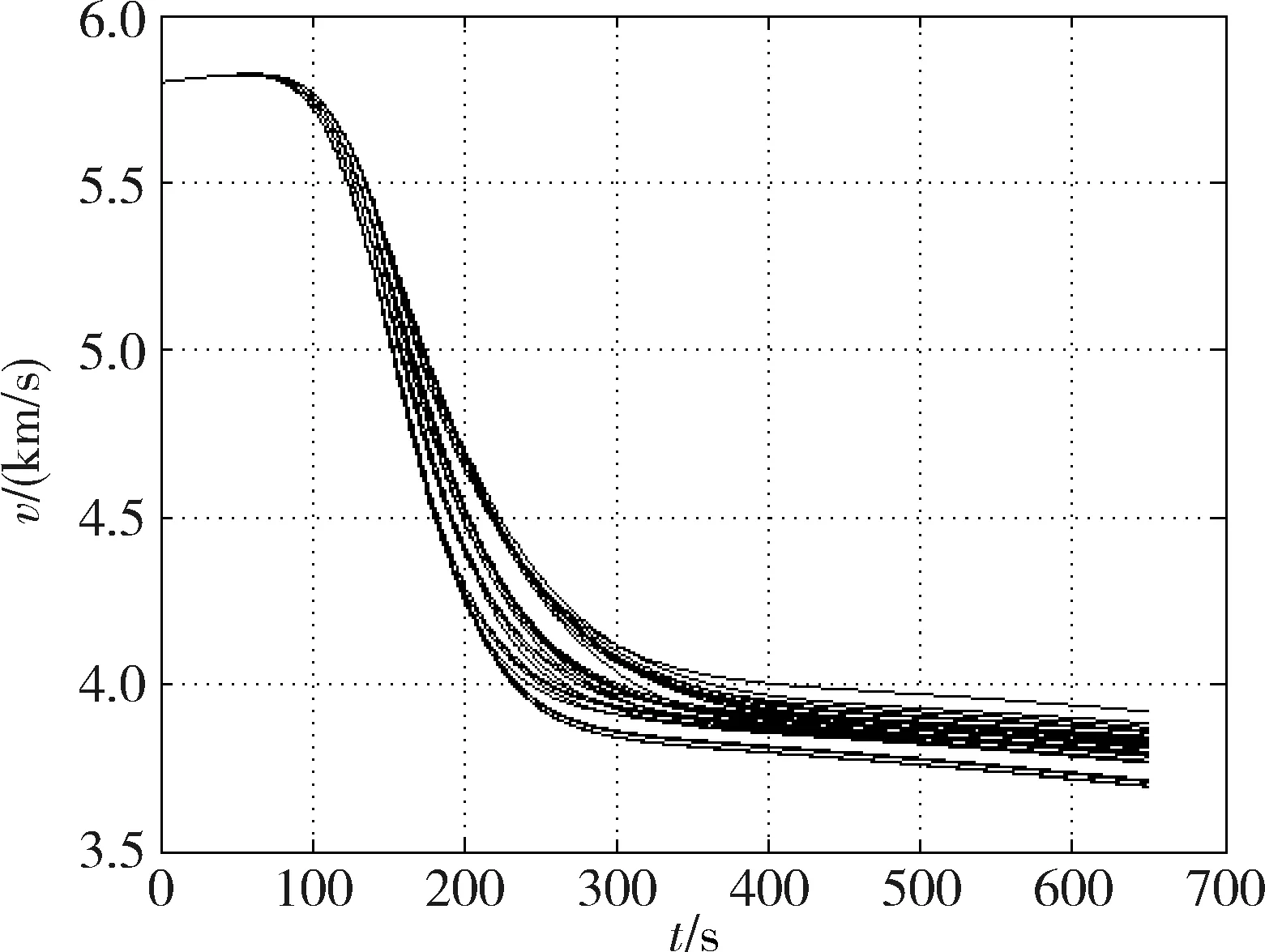
图8 速度变化曲线Fig.8 Orbit velocity histories resulting from multi off-nominal conditions

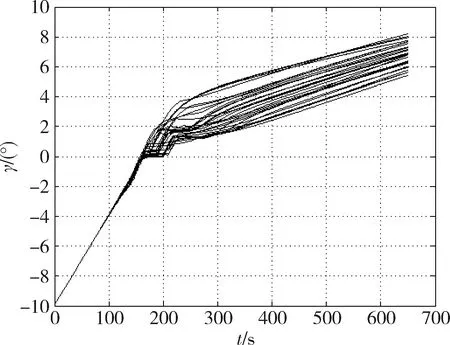
图9 飞行路径角角变化曲线Fig.9 Flight path angle histories resulting from multi off-nominal conditions

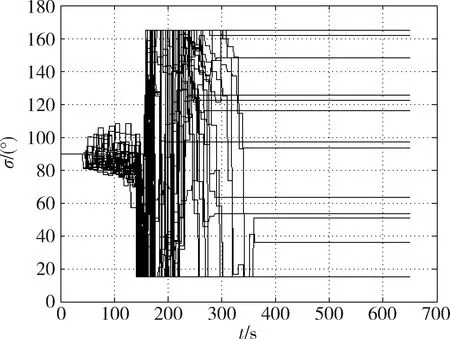
图10 倾侧角变化曲线Fig.10 Bank angle profiles resulting from multi off-nominal conditions

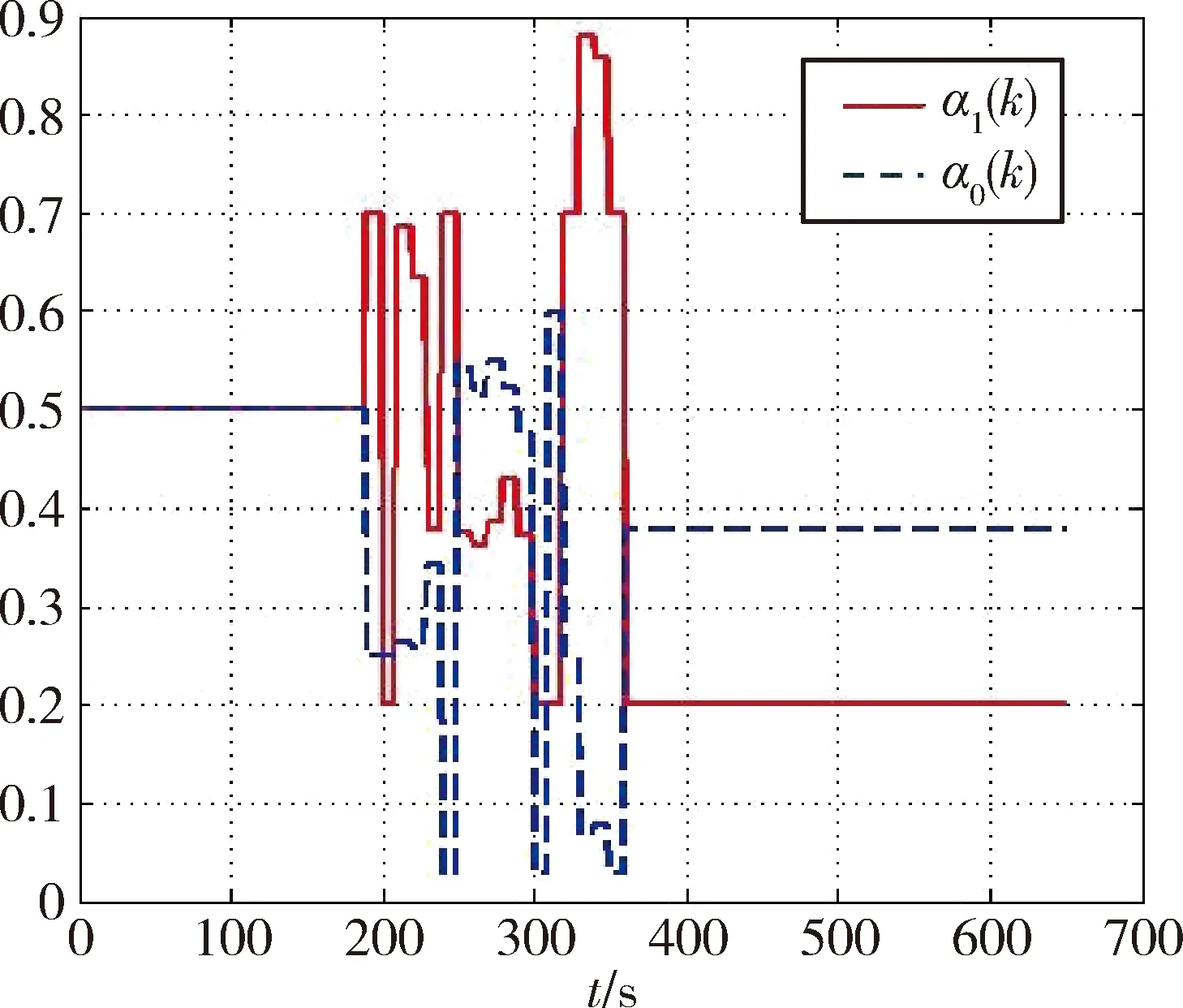
图11 特征模型参数变化曲线Fig.11 The characteristic model parameters history

4 结 论

本文针对火星气动捕获问题，提出了一种基于预测校正制导的组合式制导方法.其中纵向制导分为3个阶段，分别实现抵达巡航高度，跟踪巡航高度以迅速降低轨道能量，以及以目标远拱点半径为控制目标进行准确入轨的目的；横向采取倾侧角符号翻转的控制策略.这一方法在利用了基于特征模型的全系数自适应算法强自适应能力和免于多次迭代的优势的前提下，通过设计巡航高度和优化退出巡航速度，在满足了最大过载约束的同时还在一定程度上优化了后续变轨所需的总速度增量.仿真结果表明，该方法具有较高的鲁棒性，在节约变轨燃料方面效果显著，为日后的工程应用提供了一定的借鉴价值.