半漂浮体系斜拉桥粘滞阻尼器布置与参数优化

熊柏林，徐略勤，王 龙，李钟雄

(重庆交通大学土木工程学院， 重庆 400074)

斜拉桥根据塔、梁、墩结合方式的不同，可分为漂浮、半漂浮、塔梁固结和刚构等4种体系。其中，半漂浮体系受温度、收缩和徐变的影响较小，基本周期较长，有利于耗能减震，在大跨斜拉桥中应用最广泛[1]。研究表明，斜拉桥的抗震薄弱环节主要出现在主塔、边墩、基础以及支承连接部位[2-3]。主塔与桥墩不同，由于其高度大，轴压比高，延性较低，且受高阶振型的影响，采用延性设计比较困难。此外，主塔抗震薄弱部位常位于塔底，一旦进入塑性，塔顶残余变位很大，震后难以修复[4]。因此，国内外规范都指出主塔在设计地震作用下应保持弹性[5-6]。在纵桥向，大跨半漂浮体系斜拉桥在强震下梁端容易产生较大的纵向位移，导致伸缩装置的破坏，引发主梁与相邻跨引桥的碰撞，造成落梁震害。为了同时实现保持主塔弹性状态并防止主梁与引桥碰撞的目标，增设粘滞阻尼器是最常见的做法之一[7-8]。在横桥向，主塔处一般设置抗风支座以制约塔、梁相对运动，边墩处也往往设置横向限位装置，由此导致桥梁横向刚度很大，边墩及其基础因此成为抗震薄弱部位[9]。为了降低边墩及其基础的地震反应，可在边墩处设置横向粘滞阻尼器。可见，不论从纵桥向还是横桥向来说，阻尼器布置方式及其参数优化都是应该首要解决的问题。

本文以某新建的半漂浮体系斜拉桥为背景工程，从粘滞阻尼器耗能原理出发，分别就粘滞阻尼器在桥梁纵、横向减震体系中的作用进行研究。本文在综合考虑塔、墩、支座等关键构件抗震能力的基础上，探讨阻尼器数量和参数的优化，以期为工程建设提供技术参考。

1 粘滞阻尼器耗能原理

粘滞阻尼器一般由活塞、油缸及节流孔组成，利用活塞前后压力差使油流过节流孔产生阻尼力，如图1所示。粘滞阻尼器的阻尼力与相对速度的关系可表达为：

(1)

图1 粘滞阻尼器构造图

2 工程背景与分析模型

2.1 工程概况

某新建半漂浮体系斜拉桥跨径布置为(30+75+220+75+30)m，全长430 m，为双塔双索面组合梁结构，如图3所示。H型钢筋混凝土索塔承台以上高80 m，塔柱为矩形空心截面。主梁为双边“工”字型边主梁与桥道板的组合断面，桥宽31.6 m，中心线高3.16 m，混凝土桥道板厚28 cm。两侧边跨分别设一个辅助墩和过渡墩，其中辅助墩为分离式双柱，过渡墩为三柱式排架墩。在初步设计中，主塔处布设两个单向球钢支座；辅助墩处布设两个双向球钢支座；过渡墩处布设双向+单向球钢支座，如图4所示。

图2 粘滞阻尼器力学特征

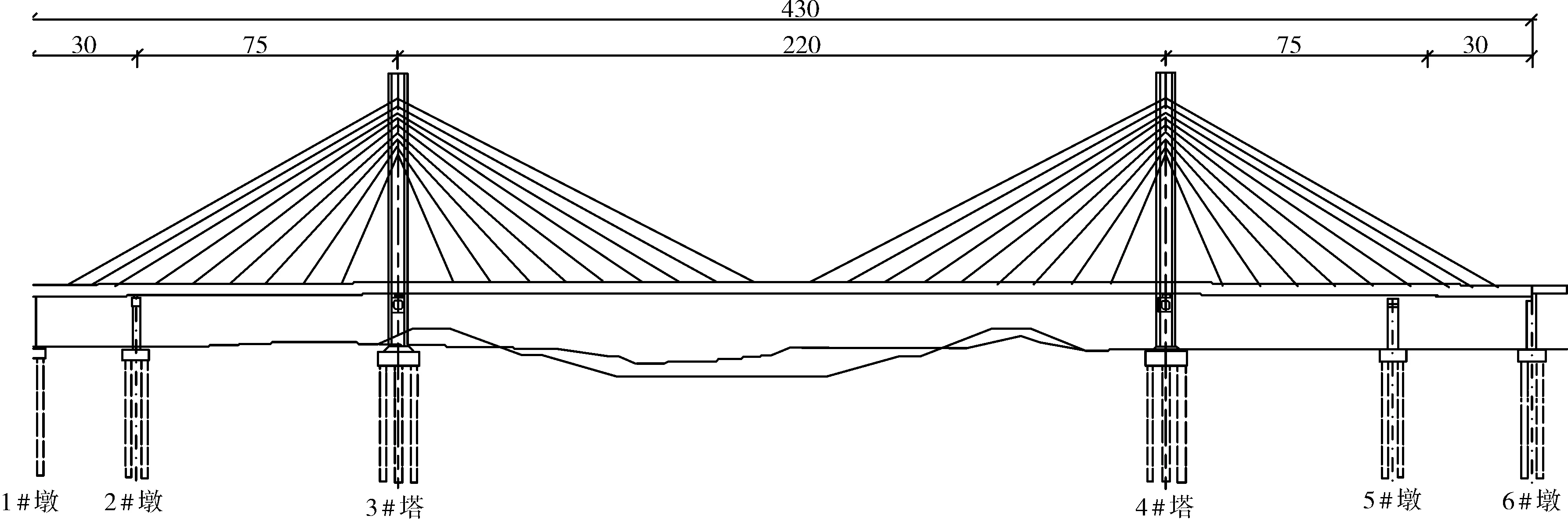
图3 斜拉桥立面布置图(单位：m)

图4 初步设计的支座布置

2.2 有限元建模

采用SAP2000建立全桥有限元分析模型，如图5所示。主梁、索塔、辅助墩和过渡墩都用空间梁单元模拟，并考虑受压构件的二阶效应；斜拉索采用只受拉空间桁架单元模拟，按Ernst公式修正垂度效应[1]，并考虑恒载初始内力引起的几何刚度影响；桩-土共同作用采用6×6集中土弹簧模拟，弹簧刚度系数根据m法计算得到；球钢支座采用双线性滞回模型模拟活动方向的滑移摩擦效应，如图5所示；粘滞阻尼器采用Maxwell计算模型[10]；体系阻尼采用Rayleigh模型，阻尼系数取3%[5]。

图5 全桥动力分析模型

2.3 地震动输入

根据地震安评报告，罕遇地震对应的峰值加速度为0.25g。地震动输入有两类，其一是安评提供的3条人工地震波；其二是3条实际地震记录，并采用小波变换来匹配场地设计反应谱，地震波及匹配情况如图6所示。在非线性时程分析时，采用纵向+竖向、横向+竖向的地震输入方式，其中人工波的竖向地震根据细则[5]采用水平地震折减的方式获得；实际波的竖向地震直接采用实际竖向地震记录。后文分析结果的包络值按6组波的平均值来考虑。

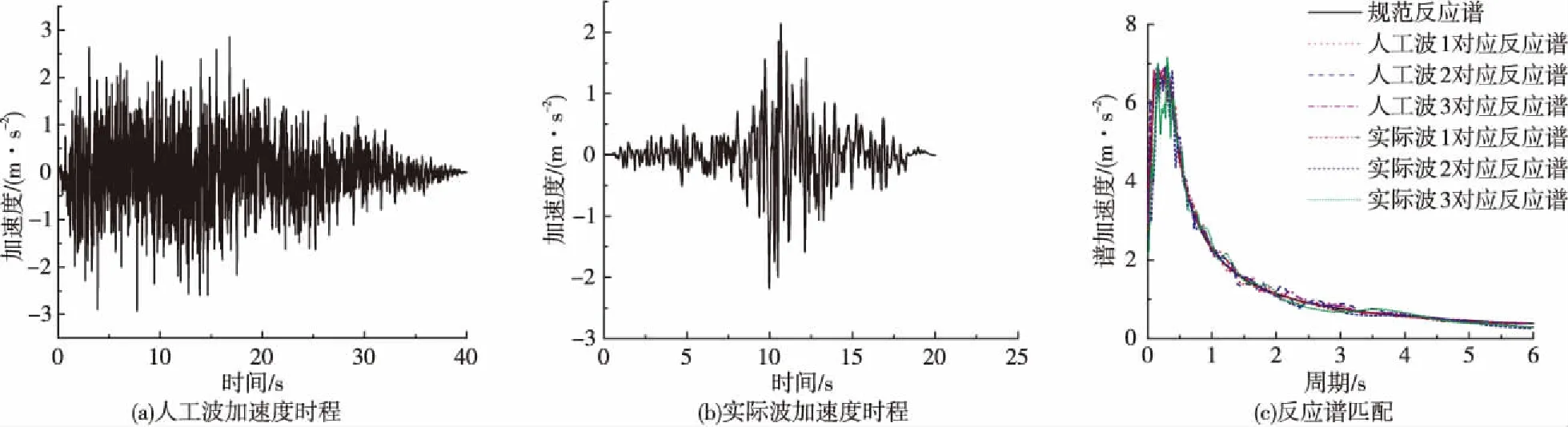
图6 地震波及匹配情况

3 分析工况

3.1 阻尼器布置方案

按照初步设计，主梁在纵桥向为半漂浮体系，其地震惯性力主要通过拉索传递至索塔，辅助墩和过渡墩分担较小。因此，阻尼器在纵桥向所起的作用是限制主梁位移，防止球钢支座变形超限，同时降低索塔的地震响应。基于此，阻尼器在纵桥向主要布置在主梁与索塔交接处，考虑造价、外形体积和便于布置等因素，阻尼器性能参数不宜过高，本文分析了3种布置方式，即分别在塔梁交接处布置1个、2个、4个纵向阻尼器，阻尼器参数分别取ξ=0.5和C=5 000 kN/(m/s)ξ。为便于表述，后文将3个工况简称为“纵-1阻尼器”、“纵-2阻尼器”、“纵-4阻尼器”。

前期分析表明，按照初步设计，主梁的横向地震惯性力主要由索塔和过渡墩承担，辅助墩由于布置双向支座，参与程度很低，导致两侧过渡墩在横桥向无法满足抗震要求。可见，本桥横向抗震问题更加突出。为了解决过渡墩横向抗震问题，本文分析了3种布置工况：1)在过渡墩双向支座的那一侧布置阻尼器；2)在过渡墩的两侧都布置阻尼器；3)将初步设计中的单向+双向支座改为2个双向支座，然后在两侧都布置阻尼器。阻尼器参数初步取ξ=0.6和C=3 000 kN/(m/s)ξ。为便于表述，后文将3个工况简称为“横-DX+SX单侧”“横-DX+SX双侧”“横-SX+SX双侧”。

3.2 关键构件抗震性能

前期分析对桥梁抗震薄弱环节进行了判别，限于篇幅，本文重点探讨过渡墩墩底截面、塔底截面和球钢支座的抗震能力(辅助墩由于设置双向支座，抗震富余量较大，未予考虑)。对钢筋混凝土构件截面进行纤维离散建模，并开展轴力-弯矩-曲率分析，可得到每个截面的初始、等效和极限抗弯能力(分别对应构件的无损伤、可修复损伤和局部破坏3个状态)，计算方法详见文献[2]。由于桥梁在立面布置上对称，表1列举了左半侧各关键构件的抗震能力，后文也以该侧(即图3中的1#墩、2#墩和3#塔)进行分析。

表1 各构件的抗震能力

3.3 减震率

为便于描述阻尼器的减震效果，后文采用减震率进行对比分析，其定义为：

(2)

式中：β为减震率；Enone为无阻尼器时桥梁的地震响应；Edamper为设置阻尼器后桥梁的地震响应。

4 阻尼器布置效果分析

4.1 纵桥向

在纵桥向，本文重点以过渡墩底截面S2和塔底截面S4为内力分析对象，以塔顶、梁端和支座为位移分析对象，计算结果见表2—3。

表2 3种方案地震内力对比

表3 3种方案地震位移对比

由表2可知，不同阻尼器布置方式对索塔内力响应的减震效果非常明显，但对过渡墩和辅助墩(限于篇幅，辅助墩的结果未列出)的影响很小，几乎可忽略。随着阻尼器数量的增加，索塔内力的减震率不断增大，如塔底S4的弯矩减震率由1个阻尼器的13.0%增大到4个阻尼器的51.1%，而1#墩底S2的弯矩减震率仅由0.9%增至3.2%；剪力的变化规律也类似。结合表1可知，在无阻尼器情况下，索塔将进入“局部破坏”状态；当设置4个阻尼器时，索塔才能保持“无损伤”状态。

由表2可知，不同阻尼器布置方式对各构件位移响应的减震效果也非常明显。无阻尼器时，塔顶位移为374.9 mm，桥塔和过渡墩处的支座变形分别达267.1和325.1 mm(辅助墩上的支座介于这两者之间，限于篇幅没有列出)；当设置4个阻尼器时，塔顶位移降至122.4 mm，减震率达67.3%，两处支座的变形分别降至77.5和129.9 mm，减震率分别达71.0%和60.0%。结合表1可知，不设置阻尼器将导致过渡墩处的支座变形超限，引发支座破坏；设置1个阻尼器或多个阻尼器都可保证全桥支座的抗震安全。

综合考虑造价和抗震安全，本桥在纵桥向建议在塔梁交接处布置4个阻尼器。

4.2 横桥向

前期分析表明过渡墩是本桥横向抗震的薄弱环节。由于过渡墩处支座布置在横桥向上不对称，框架墩的3个立柱受力不完全相同，因此本文对这3个截面均予以分析，计算结果见表4—5及图7。

由表4—5可知，在初步设计的支座布置下，在过渡墩处设置单侧和双侧阻尼器对各构件几乎没有减震效果。结合表1可知，不论是否设置阻尼器，过渡墩3个立柱都将进入“可修复损伤”状态。若将过渡墩支座布置由DX+SX改为SX+SX，并布置双侧阻尼器后，过渡墩弯矩和剪力响应会大幅下降。相比无阻尼器时，S1～S3截面的弯矩减震率分别为34.8%、37.8%和36.5%。结合表1可知，此时过渡墩将保持“无损伤”状态。值得一提的是，过渡墩约束方式的改变对索塔地震响应几乎没有影响。

由图7可知，在初步设计的支座布置下，不论是否设置阻尼器，过渡墩单向支座的剪力都大大超出其抗剪能力(见表1)，且阻尼器几乎不起作用，其原因在于阻尼器发挥功效有赖于其冲程速度(见公式(1))。由于单向支座的存在，主梁在过渡墩处的横向运动受到限制，其相对于墩的速度很小，因此阻尼器无从发挥作用。索塔处的支座剪力同样超出其抗剪能力，即使改变过渡墩支座布置后，也没有明显改善。由于索塔处设置了横向抗风支座，可有效地分担球钢支座的横向剪力，限于篇幅，本文不作重点介绍。过渡墩的抗震性能得到大幅改善，但其支座变形达69.1 mm，超过了表1中50 mm的变形能力。为此，后文对阻尼器性能参数进行了优化分析，以控制过渡墩支座的横向变形。

表4 3种方案地震弯矩对比

表5 3种方案地震剪力对比

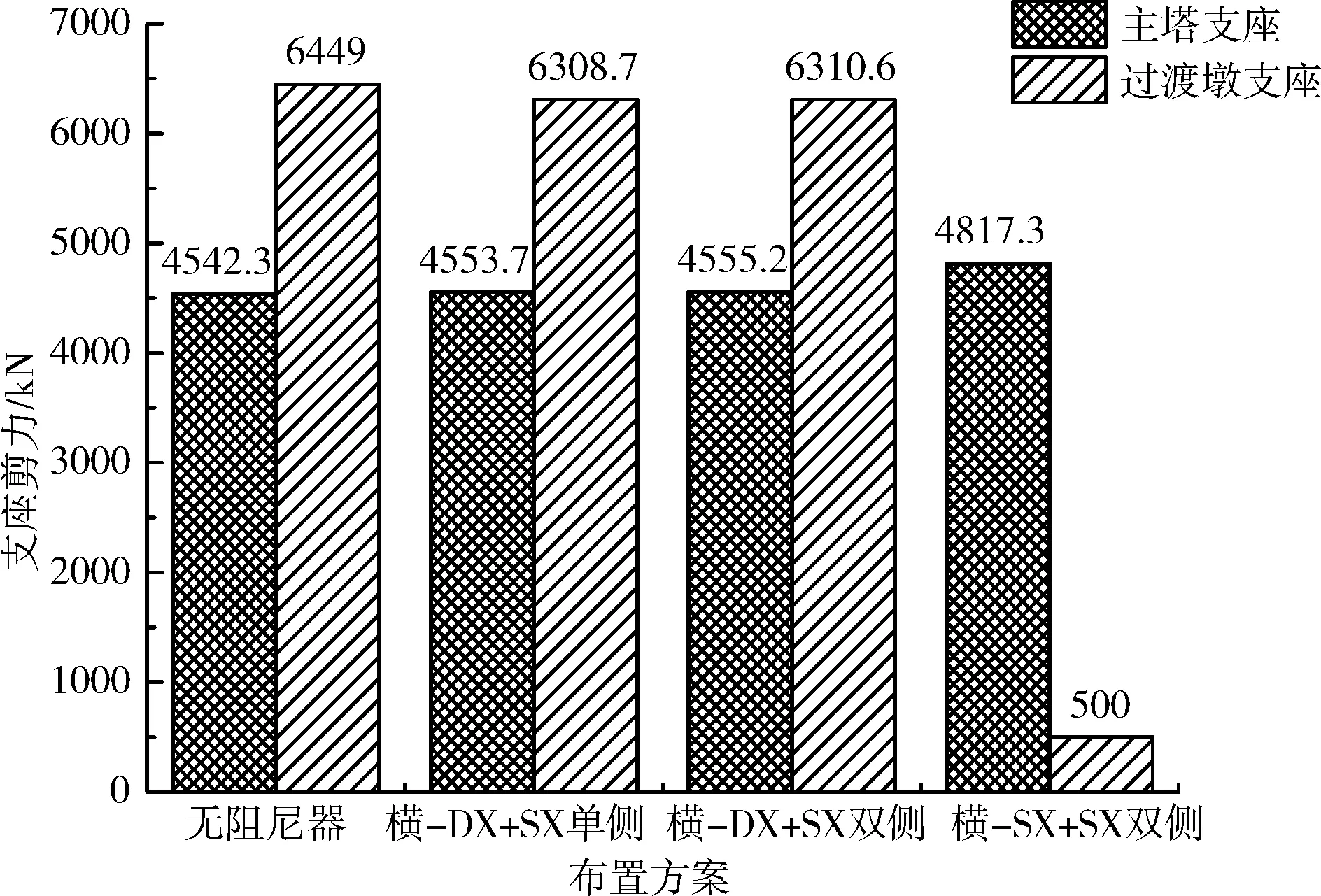
注：由于改变了支座布置，“横-SX+SX双侧”中过渡墩处已无单向支座，因此其支座剪力为摩擦力。

图7 3种方案支座剪力对比

5 阻尼器参数优化分析

由公式(1)可知，粘滞阻尼器耗能能力与性能参数C和ξ密切相关。为此，本文针对4.2节中的“横-SX+SX双侧”工况开展阻尼器参数优化分析，以讨论阻尼器性能参数对桥梁减震率的影响，同时确定保证桥梁抗震安全的合理参数，为工程设计提供依据。为了降低计算量，采用逐一优化方式来选择参数，首先保持C=3 000 kN/(m/s)ξ不变，分别令ξ=0.1，0.2，0.3，……，0.9，由此确定最优ξ值；然后保持ξ值不变，令C=1 000、2 000、3 000、4 000、5 000 kN/(m/s)ξ，由此确定最优C值。由表4—5可知，过渡墩上阻尼器布置方式对主塔几乎没有影响，因此本节重点分析过渡墩及支座的地震响应。

如图8所示，随着阻尼指数ξ的增大，过渡墩3个立柱的弯矩和剪力响应都经历了先减后增的过程。当ξ=0.7时，过渡墩内力最小。如图9所示，过渡墩支座的横向变形随阻尼指数ξ的增大而增大，满足支座容许变形时，ξ取值不能超过0.3。结合表1可知，当ξ=0.3时，过渡墩仍处于“无损伤”状态，因此阻尼指数的最优值取ξ=0.3。

图8 ξ对过渡墩地震内力的影响

图9 ξ对过渡墩支座横向变形的影响

由图10—11可知，随着阻尼系数C的增大，过渡墩内力单调增大，支座变形则单调下降。根据表1，若要保持过渡墩处于“无损伤”状态，且支座变形低于其容许值，那么阻尼器的优化参数应取ξ=0.3、C=3 000 kN/(m/s)ξ。在此参数下，过渡墩3个立柱的墩底弯矩分别为19 841.44、22 391.15、19 995.722 kN·m，均低于“无损伤”状态的弯矩；支座横向变形为47.4 mm，也低于50 mm的容许变形。

图10 C对过渡墩地震内力的影响

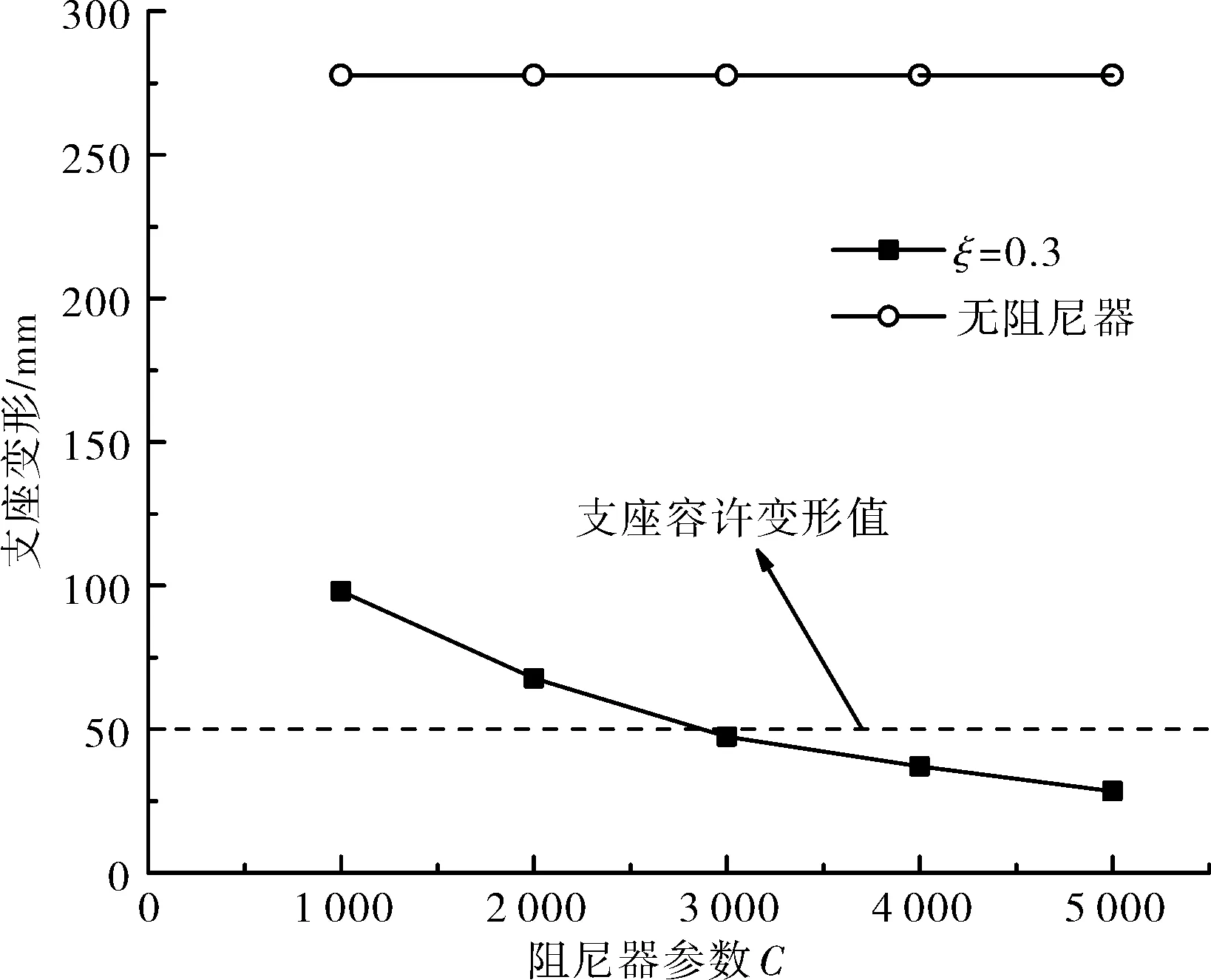
图11 C对过渡墩支座横向变形的影响

6 结论

本文针对某新建半漂浮体系斜拉桥，通过纵、横桥向阻尼器布置及其性能参数的优化分析，得到如下结论。

1)在初步设计的支座布置下，主梁在纵桥向为半漂浮体系，其地震惯性力主要通过拉索传递至索塔，辅助墩和过渡墩分担很小；而在横桥向，主梁地震惯性力主要由索塔和过渡墩承担，辅助墩由于布置双向支座，参与程度很低。

2)在纵桥向，如果不设置阻尼器，索塔将进入“局部破坏”状态，过渡墩支座的纵向变形超限。当在塔梁交接处布置4个阻尼器时，索塔可保持“无损伤”状态，支座变形也低于容许值。

3)在横桥向，若保持初步设计的支座布置，那么不论是否设置阻尼器，过渡墩都将进入“可修复损伤”状态，且阻尼器作用很小。将过渡墩支座布置由DX+SX改为SX+SX，并布置双侧阻尼器后，过渡墩地震内力会大幅下降。

4)在横桥向，过渡墩上支座和阻尼器的布置方式对索塔地震响应几乎没有影响。随着阻尼指数ξ的增大，过渡墩地震内力先减后增，而支座变形则单调递增；随着阻尼系数C的增大，过渡墩地震内力单调递增，而支座变形则单调下降。为了保持过渡墩处于“无损伤”状态，且支座变形低于容许值，那么阻尼器的最优参数分别为ξ=0.3、C=3 000 kN/(m/s)ξ。