二氧化碳在CH4-CO2二元体系中的冰点预测

孔令伟

中国寰球工程有限公司北京分公司

天然气处理大多是低温过程，而低温可能造成固体CO2积聚，从而使设备管线和阀门产生冻堵，同时也会降低分离设备的运行效率，导致乙烷收率下降[1]。因此，CO2的冻堵成为深冷分离工艺设计的限制因素之一。为防止低温过程中的CO2冻堵，在流程方案设计前需要考虑CO2的脱除顺序。

CO2三相点的温度为-56.6 ℃，而天然气深冷分离单元操作温度一般在-75～-130 ℃，从热力学上讲，当温度低于-56.6 ℃时都可能发生CO2冻堵。固体CO2的形成与原料气组成及系统的操作条件密切相关。当系统的压力一定时，固体CO2的形成温度随原料气中CO2含量的升高而升高；当原料气组成一定时，固体CO2的形成温度随压力的升高而升高，形成CO2固体的可能性增大。

脱酸单元是天然气处理中的高能耗单元，如果气体组成CO2含量较高，为防止CO2冻堵，一般考虑在进入冷箱之前进行脱除；但如果CO2含量较低，可以考虑在进入冷箱之后脱除乙烷中的CO2，这是因为此种方案需要处理的气体量小，具有较大的节能优势。为确定CO2的脱除顺序，准确预测CO2的冰点温度是十分关键的。

由于CO2的相对挥发度介于甲烷与乙烷之间，且轻烃回收装置CO2冻堵体系中，所含的烃类主要是甲烷，因此脱甲烷塔上部的气相可简化为CH4-CO2二元体系。GPSA根据研究得出了CH4-CO2体系定性相图[2]，如图1所示。

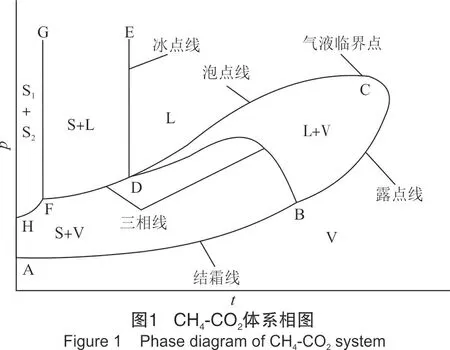
图1中，BDF为气液固三相平衡线。FH和FG也是三相线，此时CH4已成为固体，故在此不作讨论。图中AB为结霜线，当温度低于B点温度、压力大于AB线上的压力时，会从气相中析出固体。BC为露点线，CD为泡点线，C点为气液临界点。DE为冰点线，当温度低于D点温度、压力高于DF线上压力时，液相中会析出固体。ABDFH为气固区，BCD为气液区，EDFG为液固区。

国外曾有学者对天然气中固体CO2的形成问题做了一些研究，并预测了天然气中形成固体CO2的条件[3]，但是专门针对冰点温度的文献尚鲜有报道。相较而言，国内对CO2结冰问题的研究工作做得较多。易希朗[4]提出了轻烃系统CO2结晶气-液-固相平衡的热力学关系式，但是未对冰点温度进行计算。桑田[5]用逸度修正CO2的分压，提出了天然气深冷分离过程中固体CO2生成的条件，但没有给出理论的计算方法。蒋洪等[6]建立了CH4-CO2二元体系的液固模型，但是其求解过程需要迭代计算，比较繁琐。熊晓俊等[7]根据气固平衡原理，采用PR状态方程法得出CH4-CO2二元体系中CO2冰点温度的关联式，但与实验数据对比误差较大。陈赓良等[8]则分别对CH4-CO2二元体系的气固平衡及液固平衡进行讨论，分别提出了各自的关联式，但是给出的液相体系的关联式不具有通用性。

PR状态方程法计算冰点温度是一种较为通用的方法，但是计算较为繁琐。在工程应用中，通常更希望有一种简便快捷且准确的方法来计算。本研究对CH4-CO2二元体系的气固平衡及液固平衡分别进行讨论，针对气固平衡体系提出一种修正的道尔顿分压定律方法；针对液固平衡体系，对实验数据进行拟合，提出一种通用的冰点预测关联式。将本研究方法计算结果、陈赓良-朱利凯模型法计算结果、HYSYS计算结果、Aspen Plus计算结果与实验数据进行比较。

1 计算方法

1.1 气固平衡

依据道尔顿定律，在气固平衡中，气相CO2的摩尔分数(mv)是固相CO2蒸气压(pCO2s)与系统压力(p)的比值，如式(1)所示。

mv=pCO2s/p

(1)

气相中无固体CO2生成的判据是：pCO2s>pCO2(pCO2是气相中CO2的分压)。因此，mv是不出现固体CO2气相中最高容许CO2的摩尔分数。

文献[6,8-9]给出了纯组分CO2的饱和蒸气压：

T为90～158 K时：

(2)

T为138～216 K时：

(3)

文献[3,7]提出了纯组分CO2的饱和蒸气压的通用关联式，见式(4)：

pCO2s=9.44×108×EXP(-3 108.2/T)

(4)

陈赓良、朱利凯提出修正的关联式来描绘气体平衡[8]，见式(5)～式(7)：

(5)

A=(lgp-1.097 0)/1.749 9

(6)

mv=A×pCO2s/p

(7)

在非理想的二元体系中，由于有第二种气体甲烷存在，导致固体CO2的蒸气压要比纯组分的蒸气压高。因此，陈赓良、朱利凯通过添加压力校正因子的方法，对非理想的二元体系中固体CO2的蒸气压进行修正，以更准确地描述气体平衡。

美国的Agrawal、Le和Davis分别对CH4-CO2的两组分体系的气固平衡实验进行了研究，其中以Agrawal的数据最为常用[10-11]。本研究借鉴陈赓良、朱利凯思路，以纯组分CO2的饱和蒸气压的通用关联式(4)为基础，添加压力校正因子以修正pCO2s，校正因子关联式通过Agrawal实验数据进行拟合得到：

A=[(lgp)1.135-1.303]/1.749 9

(8)

mv=A×pCO2s/p

(9)

1.2 液固平衡

文献[8]给出了固体CO2在CH4液相中的平衡溶解度(ms)与温度的关联式，见式(10)和式(11)：

T为150～200 K时：

ms=1.235 99-1.649 273×102×T+

5.551 553×10-5×T2

(10)

T为122～151 K时:

lgms=-7.206 4+0.034 86×T

(11)

美国的Kurata、Davis和Cheung分别对CH4-CO2的两组分体系的气固平衡实验进行了研究，其中以Kurata的实验数据最为常用，实验结果收录在GPA的RR-10研究报告中[10，12]。通过分析其实验结果的数据分布情况可知，CH4-CO2二元液相中的平衡溶解度与温度的数据分布关系基本符合对数函数关系。因此，本研究以Kurata的实验数据为基础，首次拟合出二元液相中的ms与温度的经验公式，见式(12)。

(12)

文献[8]提出的经验公式为两段式关联式，其中式(10)和式(11)适用不同的温度范围。本文提出的关联式为单一的连续函数，便于工程计算，且具有一定的通用性。与实验结果的对比情况表明，其准确度也更高。

2 结果与讨论

HYSYS是石油天然气及化工行业广泛应用的流程模拟软件，具有强大的物性数据包以及许多便捷的计算工具包。HYSYS中的CO2Freeze Out工具包可用来计算CO2结晶析出温度。在HYSYS中选择PR状态方程和数据库默认的二元交互作用系数来计算物性。设置好物流压力p和组分xi参数,然后使用CO2Freeze Out工具,便可得知CO2在CH4-CO2二元系中的CO2固体温度。

Aspen Plus是化工行业及石油天然气行业的大型化工流程模拟软件。拥有强大的物性数据库AspenPCD、DIPPR，并可免费使用美国国家标准与技术研究院数据库NIST。且可提供德国化工与生物技术协会的数据库DECHEMA接口。Aspen Plus中的物性分析工具可用来计算CO2结晶析出温度。在Property Sets中设置CO2的结冰点物性集，便可在Analysis中添加变量及已设置的物性集进行分析。

根据参考文献[3-4]的实验数据，本文对气固、液固平衡分别应用4种方法得出结果，并进行比较，CH4-CO2气相体系中固体形成温度的预测与实验结果的比较结果见表1，CH4-CO2液相体系中固体形成温度的预测与实验结果的比较结果见表2。

由表1可知：

(1) 陈赓良-朱利凯模型法、HYSYS模拟法、Aspen Plus模拟法和本文估算法对CH4-CO2二元系中CO2结冰温度的预测偏差均较小，平均绝对偏差分别仅为1.68 ℃、2.12 ℃、1.28 ℃和1.61 ℃。最大偏差不超过5 ℃。本文估算法的平均偏差小于HYSYS模拟法及陈赓良-朱利凯模型法，大于Aspen Plus模拟法。

(2) 陈赓良-朱利凯模型法及本文估算法对体系中CO2摩尔分数较低(～0.1%)及CO2摩尔分数较高(～10%)的情况均存在较大偏差，但最大偏差仍可保持在5 ℃以内；同时HYSYS方法在低CO2摩尔分数时误差较大，约为1～4 ℃。

深冷分离系统(脱甲烷塔塔顶及冷箱)的温度多在-100 ℃左右，此时CO2摩尔分数在1%左右[13-16]。此种情况，本文估算法及陈赓良-朱利凯模型对CO2结冰点的预测均比较准确，绝对误差均可保持在1 ℃以内。

由表2可以看出：

(1) CH4-CO2二元液相体系中，采用HYSYS软件、Aspen Plus软件及陈赓良-朱利凯模型法预测的CO2固体形成温度偏差均较大，而本文给出的模型预测结果与实验数据吻合度非常高，平均绝对偏差仅为0.60 ℃，最大偏差也只有1.48 ℃。

(2) 对比陈赓良-朱利凯模型法，平均绝对偏差2.39 ℃，最大偏差4.22 ℃，本文提出的模型关联式误差小，且为单一的连续函数，具有广泛的通用性。

3 结论

本文采用不同的方法对CH4-CO2二元系中CO2的冰点温度进行了预测，得出以下结论：

(1) CH4-CO2二元气相体系中，陈赓良-朱利凯模型法、HYSYS模拟法、Aspen Plus模拟法和本文估算法对CH4-CO2二元系中CO2结冰温度的预测偏差均较小，最大偏差不超过5 ℃。本文估算法的平均偏差小于HYSYS模拟法及陈赓良-朱利凯模型法，但大于Aspen Plus模拟法。

(2) 气相体系中，陈赓良-朱利凯模型法及本文估算法对体系中CO2摩尔分数较低(～0.1%)及CO2摩尔分数较高(～10%)的情况均存在较大偏差，但最大偏差仍可保持在5 ℃以内。因此，本文估算模型适用范围可定为0.1%～10%。深冷分离系统(脱甲烷塔塔顶及冷箱)的温度多在-100 ℃左右，CO2摩尔分数在1%上下，此时本文估算法对CO2结冰点的预测非常准确，偏差基本可控制在1 ℃以内。

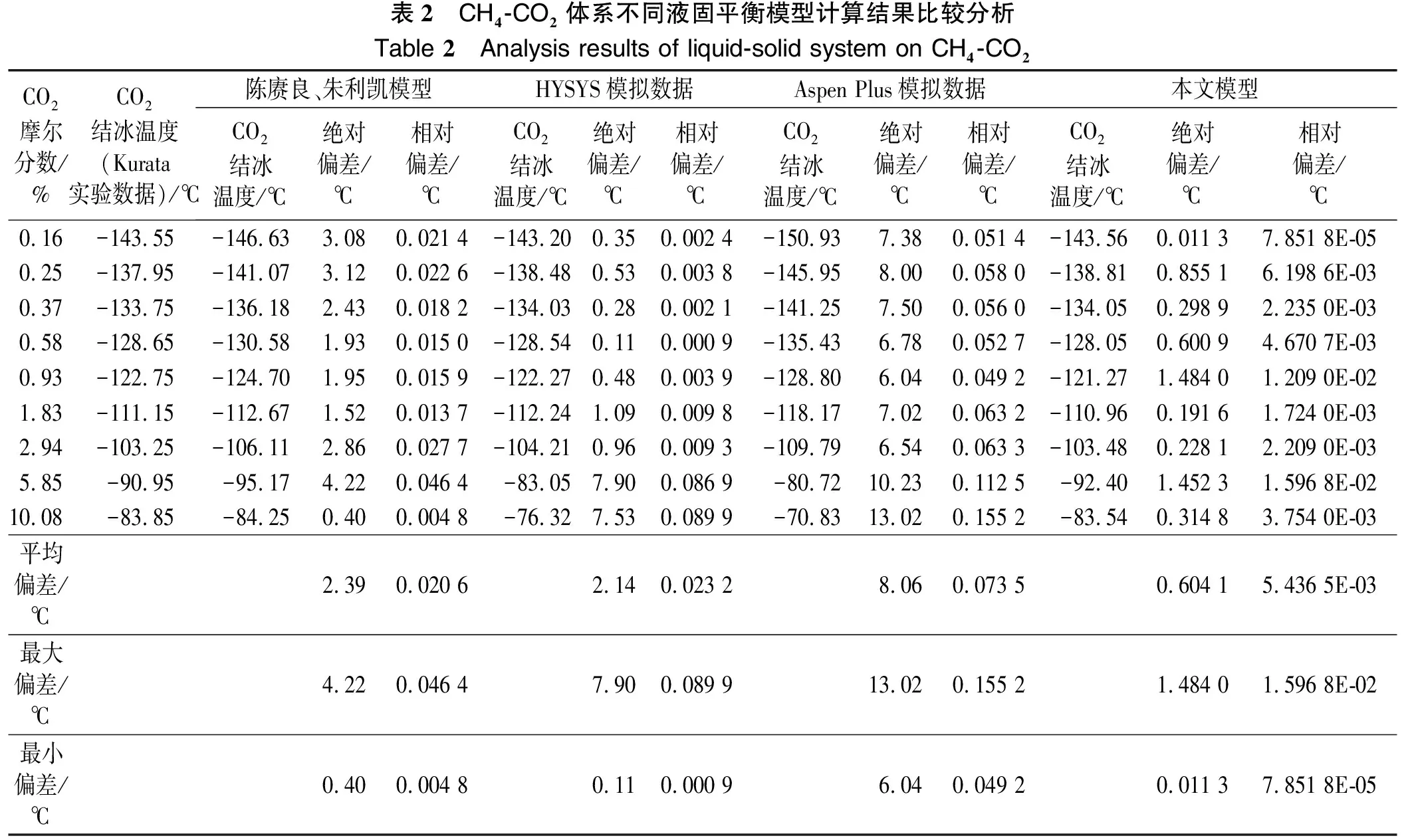
表2 CH4-CO2体系不同液固平衡模型计算结果比较分析Table 2 Analysis results of liquid-solid system on CH4-CO2CO2摩尔分数/%CO2结冰温度(Kurata实验数据)/℃陈赓良、朱利凯模型HYSYS模拟数据Aspen Plus模拟数据本文模型CO2结冰温度/℃绝对偏差/℃相对偏差/℃CO2结冰温度/℃绝对偏差/℃相对偏差/℃CO2结冰温度/℃绝对偏差/℃相对偏差/℃CO2结冰温度/℃绝对偏差/℃相对偏差/℃0.16-143.55-146.633.080.021 4-143.200.350.002 4-150.937.380.051 4-143.560.011 37.851 8E-050.25-137.95-141.073.120.022 6-138.480.530.003 8-145.958.000.058 0-138.810.855 16.198 6E-030.37-133.75-136.182.430.018 2-134.030.280.002 1-141.257.500.056 0-134.050.298 92.235 0E-030.58-128.65-130.581.930.015 0-128.540.110.000 9-135.436.780.052 7-128.050.600 94.670 7E-030.93-122.75-124.701.950.015 9-122.270.480.003 9-128.806.040.049 2-121.271.484 01.209 0E-021.83-111.15-112.671.520.013 7-112.241.090.009 8-118.177.020.063 2-110.960.191 61.724 0E-032.94-103.25-106.112.860.027 7-104.210.960.009 3-109.796.540.063 3-103.480.228 12.209 0E-035.85-90.95-95.174.220.046 4-83.057.900.086 9-80.7210.230.112 5-92.401.452 31.596 8E-0210.08-83.85-84.250.400.004 8-76.327.530.089 9-70.8313.020.155 2-83.540.314 83.754 0E-03平均偏差/℃2.390.020 62.140.023 28.060.073 50.604 15.436 5E-03最大偏差/℃4.220.046 47.900.089 913.020.155 21.484 01.596 8E-02最小偏差/℃0.400.004 80.110.000 96.040.049 20.011 37.851 8E-05

(3) CH4-CO2二元液相体系中，采用HYSYS软件、Aspen Plus软件及陈赓良-朱利凯模型法预测的CO2固体形成温度偏差均较大，而本文提出的模型预测结果与实验数据吻合度非常高，平均绝对偏差仅为0.60 ℃，最大偏差1.48 ℃，且本文给出的模型关联式具有广泛的通用性。

(4) 本文提出的估算方法仅适用于CH4-CO2二元体系，并未考虑其他组分对CO2冰点温度的影响。但在天然气深冷体系中，甲烷的组成占比很高，实际工程中仍可作为判断是否形成CO2固体的初步方法。