长江温中坝航道整治数模计算与分析
2019-05-17刘于华
戴 卓,龙 浩,刘于华
(1.重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074;2.重庆渝高科技产业(集团)股份有限公司,重庆 401121)
长江上游航道建设是国家重大战略需求,是推动上游欠发达地区和中下游发达地区优势互补、长江流域社会经济协调发展的重要措施[1]。长江叙渝段作为长江上游航道重要组成部分,对西部地区社会经济发展具有重要推动作用。据相关单位测算,叙渝段水运量至2020年和2030年分别达到7 200 万t和15 400 万t[2-3]。叙渝段为典型的山区性河道,当前受上游水利枢纽日调节非恒定下泄流量影响[4-6],枯水位时期多个月份航道通过能力不足问题凸显,地区日益增长的水运需求与航道供给能力存在较大矛盾[7]。
温中坝水道作为叙渝段重要组成部分,起着承上启下的关键作用,而该水道当前枯水期航道维护尺度仅为2.7 m×50 m×560 m(水深×航宽×弯曲半径,下同),为内河Ⅲ级航道。温中坝为温中坝水道主要碍航滩段,据水文资料观测统计,该滩结构复杂,卵石碍航严重,航道条件不够理想。本文通过建立二维数学模型模拟温中坝滩险河道情况,并初步提出整治方案措施,以满足航道条件改善需求。
1 温中坝碍航机理分析
温中坝水道起于姚坝,止于鸡母石(长江上游航道里程798.0~806.0 km,下同)。温中坝处于该水道上段,坝体将河道分为南北两槽,滩段河势(见图1)。本滩段径流受上游调控和天然降水影响,其年际变化不大,但年内分配不均。据朱沱水文站实测资料统计[8],本河段5—10月径流量占全年79.1%,11月—翌年4月仅占20.9%。其中最枯月份为2月,仅占全年的2.2%左右,最丰月份为 8月,占全年的18.5%左右。由此可见,本滩段的年径流量分配十分不均匀,且各个月份差异较大,月均最大与最小相差超过8倍。
温中坝滩段属典型的山区河流浅滩,具有“急、浅、险”等的典型特征,区域水流条件十分复杂,“剪刀水”“泡漩水”等不良流态遍布全段,岸边石嘴、石梁众多,大小礁石随处可见,地形十分复杂。当前,温中坝北槽由于礁石密布、水浅,全年处于不通航的状态;南槽为全年主航道,航道弯曲,水位5 m以下,航行条件较差。
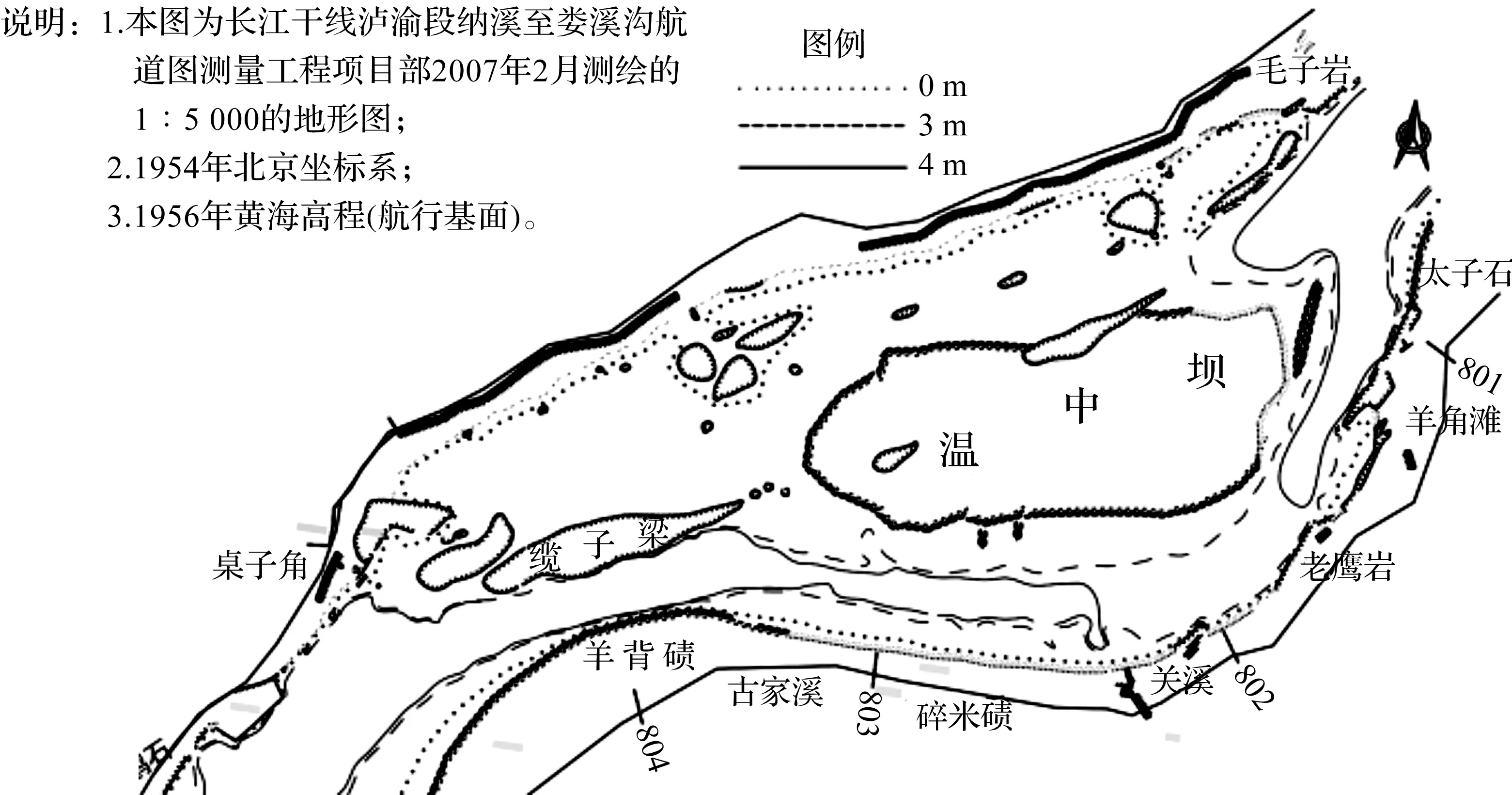
图1 温中坝滩段河势图
2 二维数学模型建立与验证
2.1 控制方程
以Navier-Stokes方程组描述河道水流运动,时均化得到Reynolds形式[9]。考虑研究河段水平尺度远大于垂直尺度,忽略水力参数的垂向加速度,假定压强服从静水分布,不计垂向的流动时间和空间的微分,将方程沿水深积分。由Bousinesq假设(忽略压强变化引起的密度变化),涡粘系数表示Reynolds应力项[10],得到平面二维河道水流控制方程:
水流连续方程:
水流运动方程:
式中:h—水深;g—重力加速度;
u—为x方向流速;v—y方向流速;
Zb—床面高程;ρ—水密度;
τsx—x方向表层切应力分量;
τsy—y方向表层切应力分量;
τbx—x方向底层切应力分量;
τby—y方向底层切应力分量;
εij—涡粘系数;f—科氏力系数。
河道岸线边界通常是不规则的,为了在平面二维模型中较好地描述河道水流运动,从而提高计算的精度和稳定性,选取计算域单元格类型显得较为重要,本文选取二次三角有限单元作为基本单元(见图2)。二次三角有限单元可随意加密计算节点,计算建模时对计算区域离散,方案处置区域局部加密,可较准确的模拟复杂边界和河道中建筑物,继而有效保证计算精度和稳定性。
图2 二次三角形六节点单元
2.2 模型建立
模型范围为上游鸡母石至下游姚坝(806.0~798.0 km),全长约8 km。模型充分利用现有地形资料,对研究河段整体塑造。模型共布置网格48 215个,其中网格间距设置约30 m,局部存在实施整治方案的河段网格加密处理,间距约为0.1~10 m(见图3)。
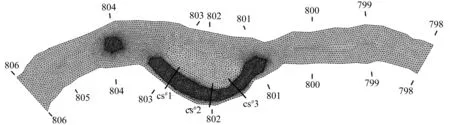
图3 模型网格
2.3 模型验证
模型验证采用资料为2015年实测的流速及水位资料(Q=4 117 m3/s)。
(1)水位验证
对比原型实测水位与模型计算水位,沿程水面线走势基本相符,水位相差基本未超过±0.1m,模型总体契合度较高,达到精度要求(见图4)。
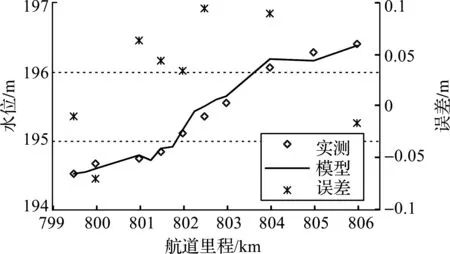
图4 水位验证(Q=4117m3/s)
(2)流速验证
实测每个测流断面分布5~14个测点,对比模型断面流速与原型断面流速分布,二者符合程度较高,各测流断面的表面流速基本吻合,最大误差保证在±10%以内,能够达到模型的精度要求(见图5)。
(3)流场验证
对比模型流场与浮标流速,除极个别测点外,模型与原型流速偏差均≤±10%,且绝大多数测点流速差值在±0.10 m/s内或<±5%,模型流场与原型流场基本达到相似要求(见图6)。
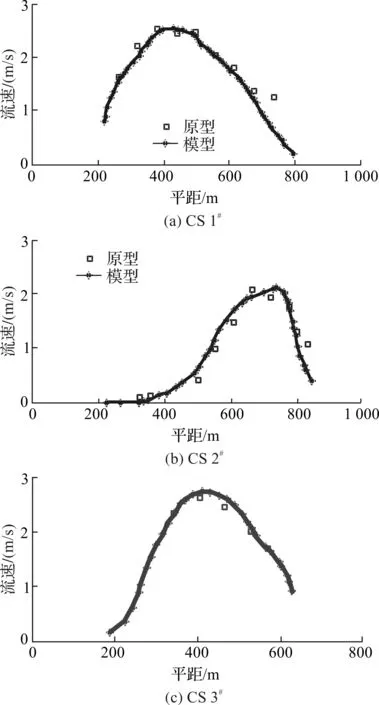
图5 流速验证(Q=4117m3/s)

图6 局部流场验证(Q=4117m3/s)
3 整治思路及方案
3.1 整治思路
(1)本文拟以国家内河II级航道标准(3.5 m×60 m×800 m)对南槽进行整治设计。当前温中坝南槽3.5 m等深线未能全线贯通,据此应疏浚航槽内浅区,使航槽内水深达到3.5 m的标准。此外,南槽尾部羊角滩存在部分暗礁,枯水期区域流态紊乱,需清礁处理。
(2)温中坝南槽中部疏浚区流速较缓慢,易造成卵石淤积,考虑在右岸修建潜丁坝束水,与疏浚同时进行,达到保持该处航道稳定的目的。
(3)温中坝滩段上游进口处有一碍航浅滩缆子梁长约500 m,缆子梁附近为大深槽,严重破坏进口处分流比,考虑在其附近筑丁顺坝改善南北槽分流比;另一种研究思路为在深槽处修建两条潜丁坝束窄水流,集中冲刷。
3.2 整治方案
(1)方案1
整治方案1主要包括挖槽清礁和筑坝束水两部分。挖槽清礁包括:疏浚温中坝南槽浅区,两侧以航槽为边界,布置1#、2#、3#挖槽3处,左右以189 m等高线为边界,挖槽深度为设计水位以下3.7 m(留出20 cm富余航深);清除羊角滩附近礁石,此处有泡漩,横流,流态较坏,布置清礁区以清除礁石,边界以189 m等高线为准,清礁范围为设计水位以下3.7 m(留20 cm富余航深)。筑坝包括:在南槽凹岸布置1#、2#、3#丁坝以减小曲率、减弱斜流,保持挖槽稳定性;在缆子梁尾部建1#丁顺坝改善分流比,以配合疏浚工作,具体布置及整治措施(见图7)。
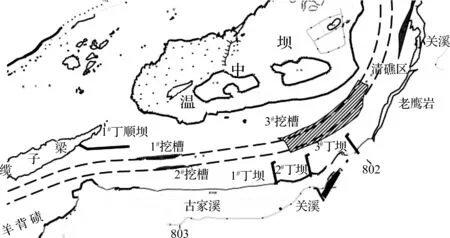
图7 方案1布置平面图
(2)方案2
方案2主要的挖槽清礁布置方案1相同,筑坝方案中除了在南槽凹岸布置1#、2#、3#丁坝外,还拟在缆子梁附近深槽布置1#、2#两条潜坝以束窄水流,以集中冲刷。具体布置及整治措施(见图8)。
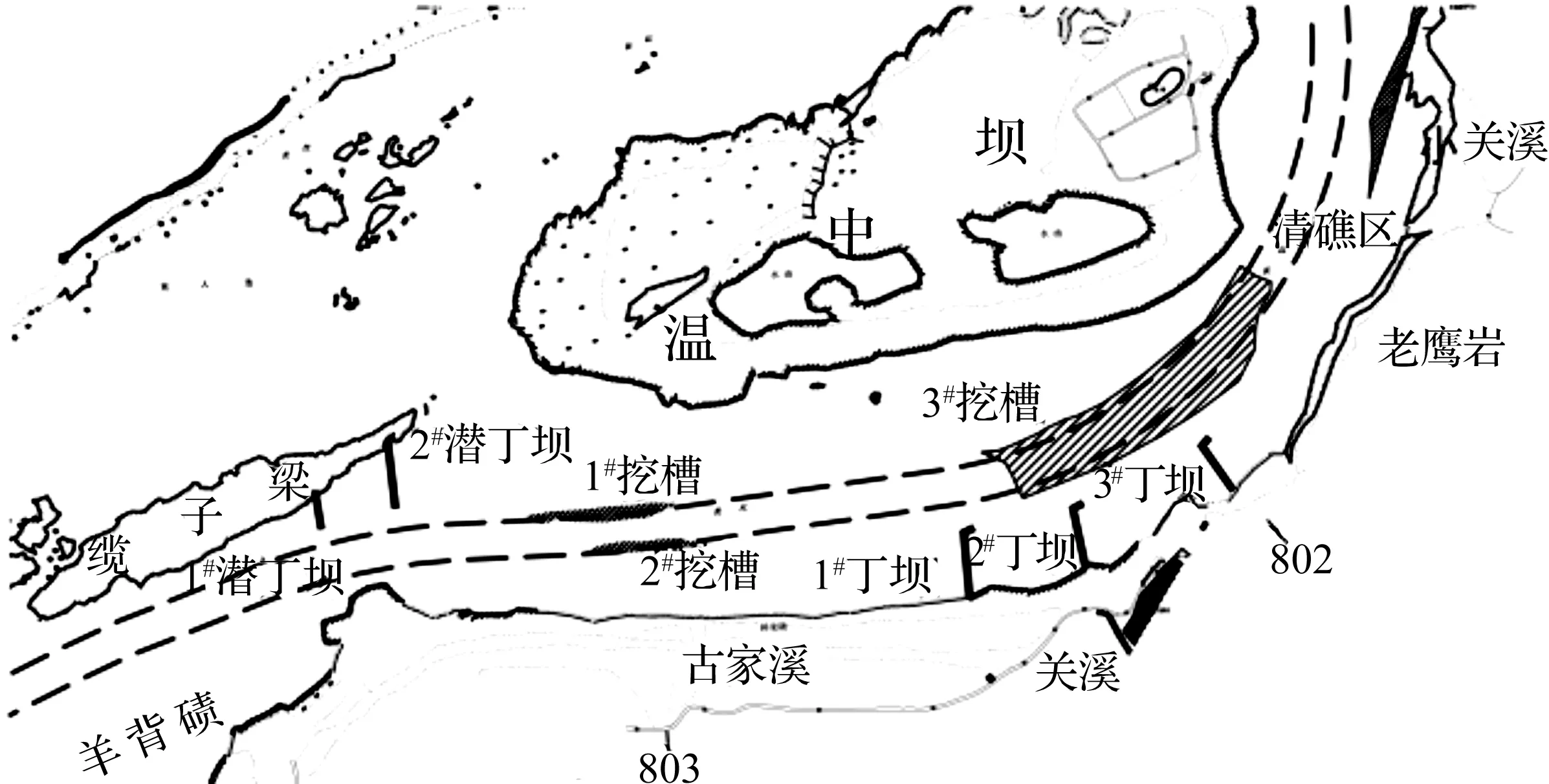
图8 方案2布置平面图
4 数模方案效果分析
4.1 通航水流条件
4.1.1 分流比分析
模型在未添加整治方案前,南槽的分流比随流量的增大而减小。整治方案后模型在设计水位(流量Q=2 230 m3/s)至整治水位(流量Q=6 530 m3/s)变幅间,南槽分流比较方案前均有所增加,其中方案1较方案前增加2%~7%,方案2增加1%~3.5%。而模型达到多年平均流量(Q=8 320m3/s)时,方案1分流比增幅减小,较方案前仅增加了4%;方案2增幅达到了3.7%。总体来看,模型添加整治方案条件下分流比方案2较方案1的改变略小,各级流量下南槽分流比变化(见图9)。
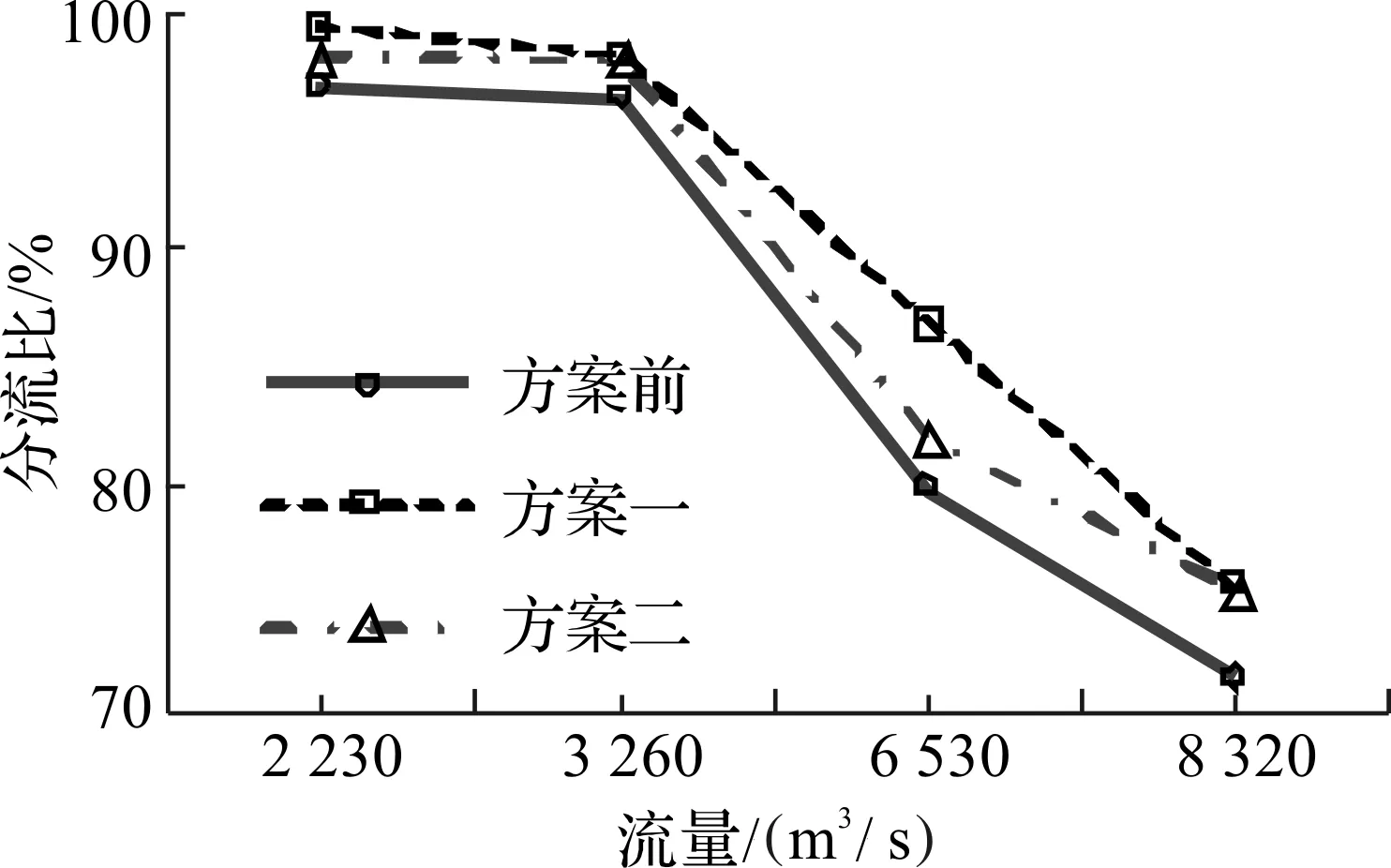
图9 各级流量下南槽分流比
4.1.2 消滩指标对比
据长江上游叙渝段2 000 t级船舶自航上滩标准,做出温中坝滩段设计水位下的通航水力指标与船舶上滩指标的对比(见图10)。其中,本滩段南槽进口处羊背碛比降为2.04‰,上行航线最大流速为2.82 m/s,超过2 000 t级船舶自航上滩标准。
为了方便分析,将流速、比降指标合为一个综合指标E,其表达式见式:
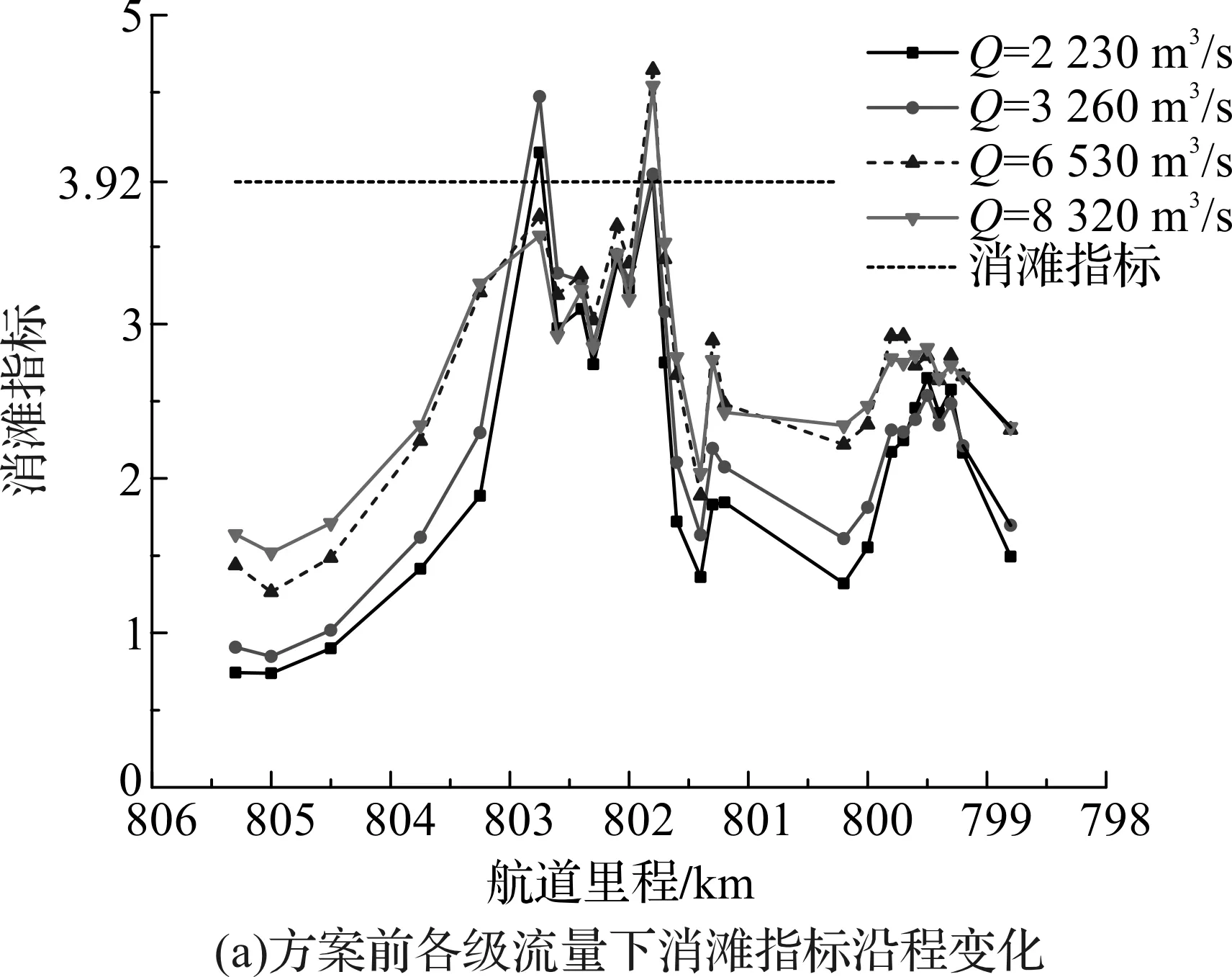
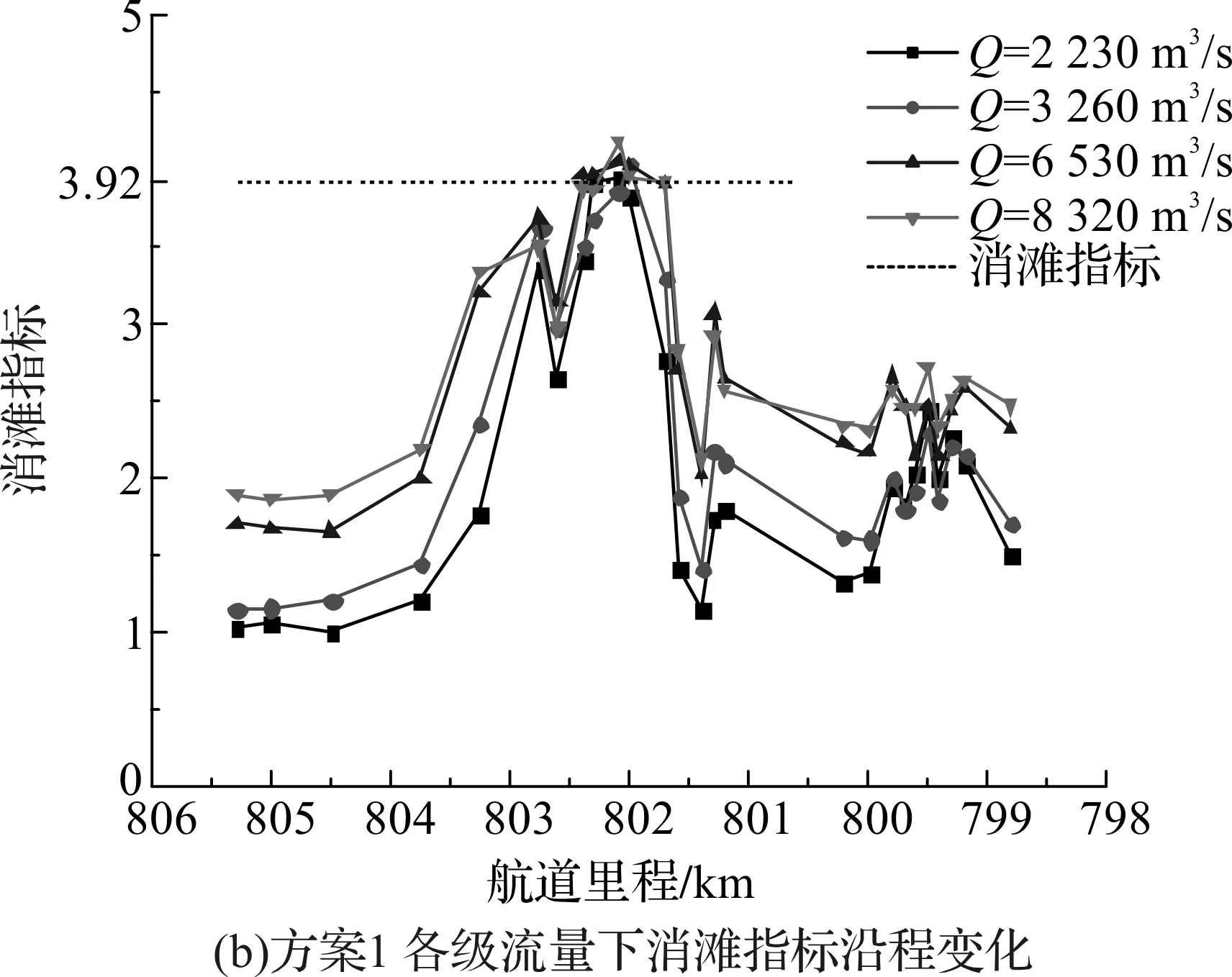
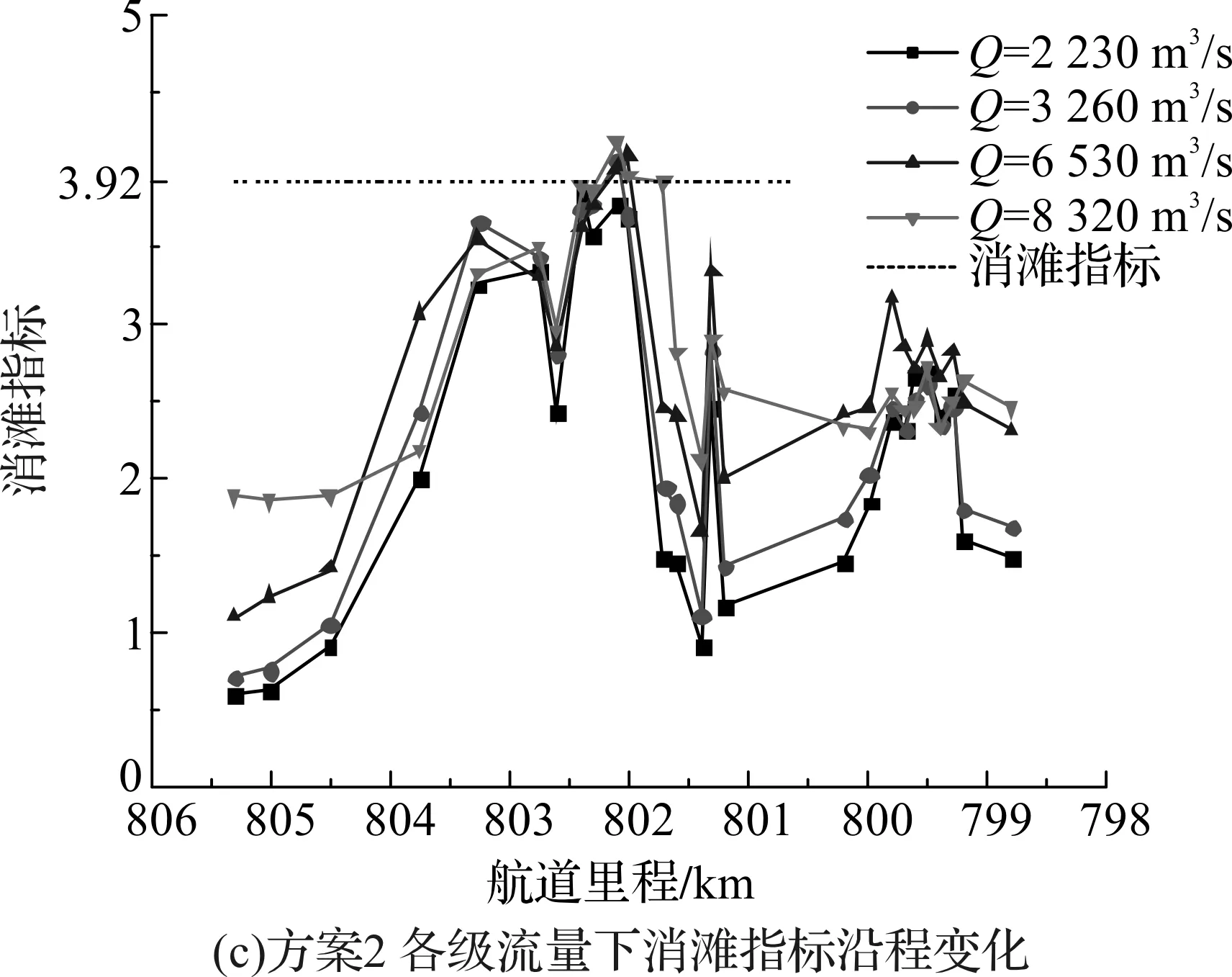
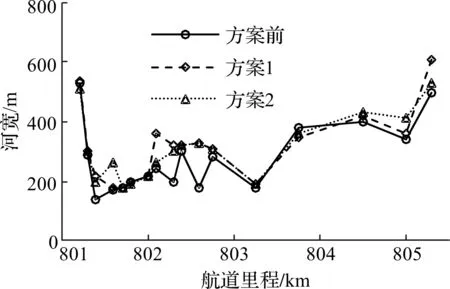
E=V+0.628J (1) 式中系数0.628为比降的当量流速,可理解为1‰的比降产生的坡降阻力与0.628 m/s的流速形成的水流阻力相当。3.92 m/s为0比降时2 000 t级船舶自航上滩限制流速。按上式,若E<3.92,则船舶可自航上滩。以方案前水流模拟成果,按式(1)绘制设计航槽内各级流量消滩综合指标E(见图11(a))。据方案实施后的计算结果,绘制设计航槽内各级流量消滩综合指标E分别(见图11(b)、11(c))。 图10 设计水位下通航水力指标与船舶上滩指标 图11 整治方案下消滩指标沿程变化 由图11可见整治方案前南槽中上段(806~803.5 km)E<3.92,未形成急滩;而中下段(803~801 km)E>3.92,最大值接近4.7,形成枯水急滩。经整治方案的筑坝、挖槽和清礁方案实施后,南槽消滩指标有一定幅度的减小,设计流量下均不形成急滩(E<3.92),且各级流量下基本上都能够实现船舶的自行上滩,其中设计流量下航槽内流速比降组合都能满足2 000 t船舶上行要求;整治流量和多年平均流量下,仅有极个别点不能满足要求,期中方案一消滩指标达到最大为4.18,方案二消滩指标达到最大为4.20,考虑方案后河宽有所增加的情况,船舶行驶过程中调节余地较大,因此2 000 t级船舶的航行要求是能够得到满足的。 4.2.1 水位变化分析 统计方案实施后本滩段在设计水位时航槽沿程水位(见图12)。温中坝上段缆子梁处的筑坝和中段的挖槽导致的南槽分流增加,使羊背碛段和南槽入口段较方案前有所升高,最大增加约0.45 m。南槽下段的挖槽和羊角滩处的清礁整治后,802 km处水位略微降低0.01~0.07 m。而方案2由于潜坝作用,较方案1在南槽入口处水位更高,其余段差异不大。总体看,两个方案实施后,本滩段上游水流均变得平缓,对于船舶通航有所改善;中下段沿程水位变幅不大。 4.2.2 河宽变化分析 根据数模计算结果,绘制3.5 m沿程等深线比较各方案河宽变化。其中,方案1在羊背碛河段平均拓宽了10~30 m;中段较方案前增加了20~150 m,满足3.5 m水深要求的河宽在180~360 m之间;下段羊角滩经过疏浚清礁后,较方案前增加10~80 m,满足3.5 m水深要求的河宽在220~540 m之间。方案2在羊背碛河段平均拓宽了10~30 m;中段较方案前增加20~120 m,满足3.5 m水深要求的河宽在180~330 m之间;下段羊角滩经过疏浚清礁后,较方案前增加10~60 m,满足3.5 m水深的河宽在200~300 m之间。设计流量下沿程3.5 m河宽变化(见图13)。 图12 设计流量下沿程水位变化 图13 设计流量下沿程3.5m河宽变化 建立的数学模型及验证计算的水面线、流速分布等与原型实测资料基本吻合,可用于进行航道整治模拟计算。模型通航水流条件和航道尺度改善情况表明:两个方案整治后本滩段水流平缓,流态良好,通航水流条件和通航实际尺度明显改善。综合比较后,整治方案1在分流比、消滩指标及尺度改善效果方面较好于方案2,且工程量要较方案2更小,推荐方案1为整治方案。本文的整治方案通过平面二维数学模型计算得到水流特性,并进行分析比选,缺乏输沙和航槽稳定性的分析,下一步需确定方案进行定床输沙及动床输沙试验以完善河床稳定性研究。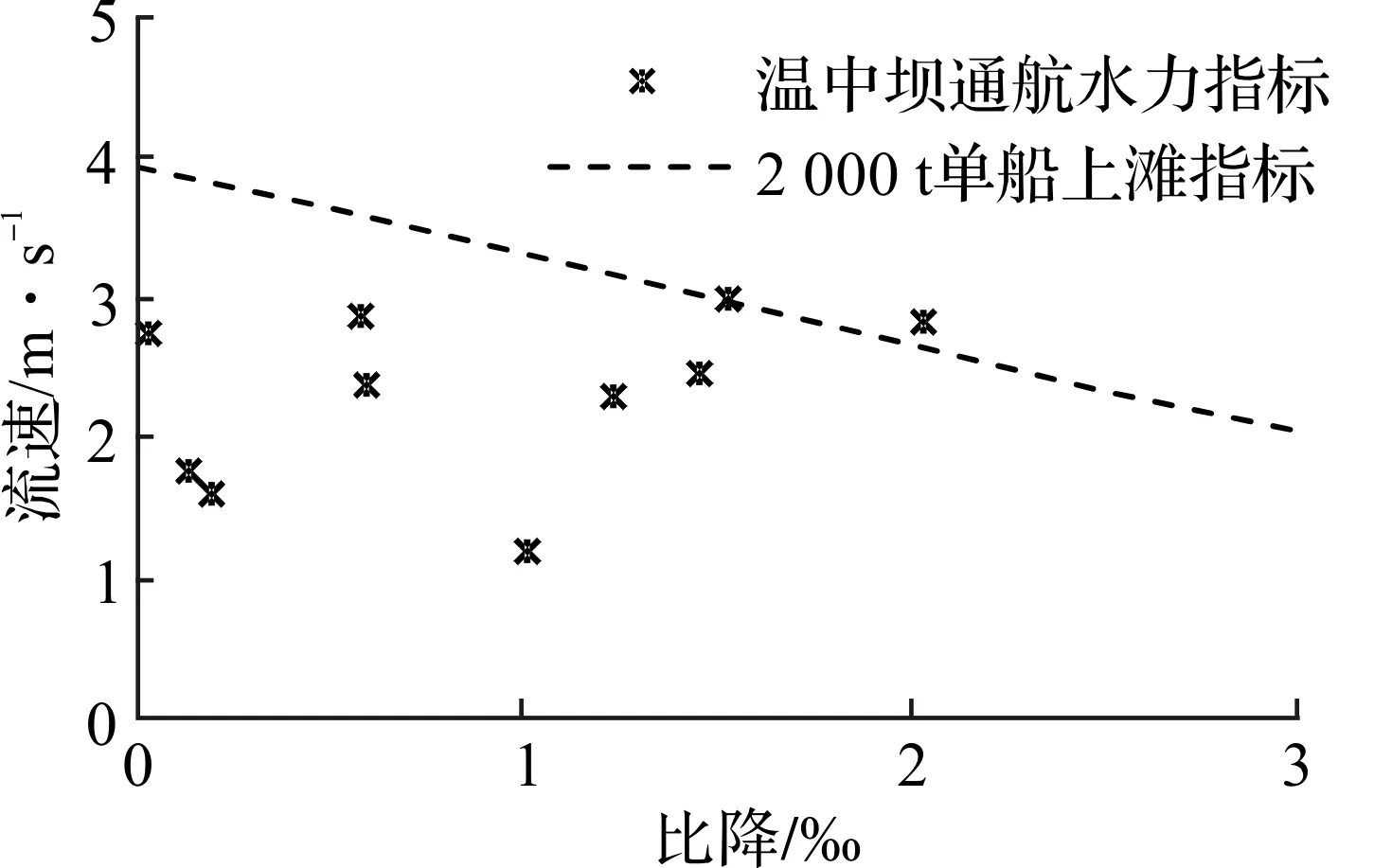
4.2 航道尺度条件

5 结论
