过渡金属硼碳化物TM3B3C和TM4B3C2稳定性和性能的理论计算*

胡前库 侯一鸣 吴庆华 秦双红 王李波 周爱国

1) (河南理工大学材料科学与工程学院,河南省深地材料科学与技术重点实验室,焦作 454000)

2) (燕山大学,亚稳材料制备技术与科学国家重点实验室,秦皇岛 066004)

在过渡金属轻元素化合物中,寻找新的硬质或者超硬材料是当前的一个研究热点.目前寻找范围多集中在过渡金属硼化物、碳化物和氮化物等二元体系,三元相的研究则相对较少.本文以已知Nb3B3C和Nb4B3C2结构为模板,采用元素替代法构建了29种TM3B3C (TM为过渡金属元素)结构和29种TM4B3C2结构,采用基于密度泛函理论的第一性原理计算方法,成功找到了热力学、动力学以及力学都稳定的Ta3B3C和Ta4B3C2两种新相.结构搜索计算确认了这两相为全局能量最优结构.能带结构和态密度的计算显示这两相均为导体,导电性主要源于Ta原子的d电子.这两种新相的硬度大约为26 GPa,说明Ta3B3C和Ta4B3C2属于高硬度材料,但不是超硬材料.

1 引 言

硬质或者超硬材料(维氏硬度大于40 GPa)因其具有高的硬度和强度、良好的抗摩擦磨损能力以及优异的化学稳定性等特点,在地质勘探、航空航天、机械加工等领域发挥着重要的作用[1].传统超硬材料存在于轻元素B,C,N,O结合所形成的强共价键化合物,比如早期发现的金刚石和立方BN,以及后期预测或实验合成的c-BC2N,c-BC5,B6O,C3N4等[2-4].该体系内除了涌现的这些新型超硬材料以外,已有的金刚石和立方BN的研究最近又有了很大进展[5-7].燕山大学田永君课题组[5-7]以洋葱结构纳米颗粒为前驱物,成功地合成了纳米孪晶的金刚石和立方BN,使得两者硬度均有了较大幅度的提高.上述传统超硬材料优势是具有很高的硬度,但是缺点在于合成条件(温度和压力)往往比较苛刻.

寻找合成条件温和的新型硬质或者超硬材料,是材料研究领域的一个热点.基于材料硬度测试方法,可知超硬材料应具有较强的抵抗弹性变形和塑性变形的能力.过渡金属具有较高的价电子密度从而具有较高的弹性模量,比如金属锇的体弹模量和金刚石的相当,具有极强的抗压缩变形能力,但是其硬度仅有4 GPa,远低于金刚石的硬度.这源于过渡金属单质中,原子间为金属键,缺乏化学键的方向性,不能有效阻止位错的产生和移动(塑性变形).如能在过渡金属结构中引入轻质非金属元素(B,C,N等),则可以在保持高价电子密度的同时,形成短而强的方向性共价键,从而可以抵抗塑性变形,进而提高材料硬度.这正是第二类硬质(超硬)材料—过渡金属轻元素化合物的设计思路[8].

过渡金属轻元素化合物的研究主要集中于硼化物、碳化物和氮化物.过渡金属硼化物体系中,2005年Cumberland等[9]成功合成了硬质材料OsB2,其硬度超过20 GPa.2007年Chung等[10]采用电弧熔炼的方法成功得到了ReB2.需要特别指出的是,上述两种过渡金属硼化物都是在常压条件下就可以获得.最近W-B体系内的稳定化合物也得到了充分研究和预测[11,12].过渡金属碳化物体系中,比较常见的化合物有TiC,ZrC,HfC,VC,NbC,TaC等.过渡金属氮化物体系中,2004年著名高压科学家毛河光课题组[13]采用高温高压方法成功合成了PtN2.随后不久过渡金属氮化物OsN2和IrN2也被成功合成[14],这些过渡金属氮化物均为极难压缩材料.关于过渡金属轻元素化合物的更多信息,可参阅综述文献[2,15,16].

从以上文献可以看出,过渡金属轻元素化合物的研究主要集中于二元相,三元相的研究则相对少见.鉴于B,C,N三种元素在周期表中位置相邻、原子大小相似、核外电子排布相近,因此过渡金属轻元素三元化合物的存在是完全可能并且合理的.相对二元相,三元相成分的复杂性决定了其结构和性能的多样性和可调性.2001年,Hillebrecht和Gebhardt[17]以Nb,B和C作为原料,以Al-Cu合金作为助溶剂,成功得到了Nb3B3C和Nb4B3C2晶体.考虑到不同过渡金属元素的价电子排布相似、原子大小相近,因此有理由相信,具有和Nb3B3C和Nb4B3C2化合物相同结构的其他过渡金属TM3B3C和TM4B3C2(TM= transition metals)化合物应该存在,这样的稳定化合物期待我们去探索发现.

随着计算理论的不断优化与完善,通过计算预测稳定相来指导实验合成,取得了很多成功的先例.结构预测的方法可以大致分为两种：1)以已知结构为基础,以化学成分相近的元素进行替代的方式,产生新结构,结构优化之后,获得最低能量的最优结构.这种方法的优点在于构建结构模型简单,计算量小.但缺点是依赖于已知结构,有可能会漏掉能量更低的全局最优结构.2)基于最新发展的遗传算法[18]和粒子群优化算法[19]结合第一性原理计算来预测结构.该类方法在寻找某种成分的全局最优结构方面,已经有了很多成功的例子,发表了多篇高水平论文.但缺点在于计算量很大,在不确定某种成分是否存在新稳定结构的前提下,盲目进行结构搜索,很多情况下往往会无功而返.

本文将上述两种结构预测方法结合使用.这是因为周期表中相近元素具有相同结构的可能性大(类质同晶现象),因此首先采用第一种方法,以Nb3B3C和Nb4B3C2结构为基础,用其他过渡金属原子TM替代结构中的Nb原子,构建多种成分的TM3B3C和TM4B3C2结构模型.采用基于密度泛函理论的第一性原理计算方法,通过计算所建结构的形成焓、声子谱和弹性常数,判断其热力学、动力学和力学稳定性,初步筛选出稳定的TM3B3C和TM4B3C2化合物.对这些初步确定为稳定的化学组分TM3B3C和TM4B3C2,采用第二种结构预测方法,寻找该组分的全局最优结构,确认第一种方法找到的稳定结构拥有全局能量最小值.

2 计算方法

本文第一性原理计算采用基于密度泛函理论的平面波赝势方法,具体计算由VASP (Viennaab-initiosimulation package)软件包[20]来完成.交换关联采用广义梯度近似(GGA)下的Perdew-Burke-Ernzerhof泛函进行处理.Nb,Ta,B,C原子的4p64d45s,5p65d36s2,2s22p,2s22p2电子作为价电子处理.平面波截断能设为600 eV.布里渊区积分采用Monkhorst-Pack形式的特殊K点方法,K点精度设置为 2π × 0.03 Å-1.在结构优化过程中,未做任何限制,即晶胞参数和原子位置均可被优化.优化过程中能量迭代收敛标准为1 × 10-5eV/atom.弹性常数的计算采用应力应变方法[21].声子谱的计算采用有限位移法,由VASP软件和PHONOPY软件[22]结合计算完成.

3 计算结果与讨论

3.1 结构搜索及热力学稳定性

Nb3B3C和Nb4B3C2同属正交晶系,空间群皆为Cmcm(No.63).表1列出了优化之后Nb3B3C和Nb4B3C2的结构参数.可以看出计算的晶格参数比文献中实验值稍大,这也是GGA泛函的一贯问题,但误差在1%以内,说明了本文计算方法的可靠性以及计算结果的可信性.

表1 Nb3B3C,Nb4B3C2,Ta3B3C和Ta4B3C2晶体的结构参数Table 1.Structural parameters of the Nb3B3C,Nb4B3C2,Ta3B3C and Ta4B3C2configurations.

Nb3B3C晶体结构如图1(a)和图1(b)所示.从图中可以看出,该结构晶胞可以划分为两类区域：Nb-C区和Nb-B区.在Nb-C区中,Nb原子和C原子形成岩盐矿NaCl型结构,C原子位于Nb原子所形成的八面体中心,每个C原子配位数为6,形成6个Nb—C键,键长范围在2.142—2.273 Å之间,与二元化合物Nb2C中Nb—C键长(2.191—2.218 Å)相当.在Nb-B区中,Nb原子和B原子形成AlB2型结构,B原子位于6个Nb原子所形成的三棱柱中心,Nb—B键长范围在2.394—2.456 Å之间,与二元化合物中NbB2中Nb—B键长2.428 Å相当.B原子的排列类似石墨中碳原子分布方式,呈蜂窝状,每个B原子除了与三棱柱顶角的6个Nb原子成键以外,还与相邻的3个B原子成键,因此B原子的配位数为9.

图1 (a),(b) Nb3B3C和(c),(d) Nb4B3C2的晶体结构(棕球,Nb原子;蓝球,B原子;粉球,C原子;Nb6B三棱柱和Nb6C八面体分别用绿色和褐色表示)Fig.1.Crystal structures of the (a),(b) Nb3B3C and (c),(d) Nb4B3C2.The light brown,blue and pink spheres represent Nb,B and C atoms,respectively.The Nb6B trigonal prisms and Nb6C octahedrons are painted green and dark brown.

如图1(c)和图1(d)所示,Nb4B3C2结构中原子排列方式和Nb3B3C结构中相似,基本组成单元相同,区别在于Nb-C区中八面体层数的不同.由于这种结构的相似性,使得两种结构中键长相近,从而造成两种结构晶格参数a和c数值也相近.

本文选择元素周期表第Ⅲ,Ⅳ,Ⅴ周期中除La系以外的所有过渡金属(TM= Sc—Zn,Y—Cd,Hf—Hg)作为替代元素,替代Nb3B3C和Nb4B3C2结构中Nb原子,形成29种TM3B3C和29种TM4B3C2.首先讨论这29种TM3B3C化合物的热力学稳定性.对于一个热力学稳定的三元化合物来说,不能分解成相应单质、二元相以及其他三元相的任意组合.但是分解产物的组合方式往往有很多种,计算判断比较繁琐复杂.因此首先通过判断TM3B3C化合物相对于三种单质材料的稳定性,从而先排除一部分不稳定的TM3B3C相.三种单质材料生成三元TM3B3C相的化学反应方程式如下：

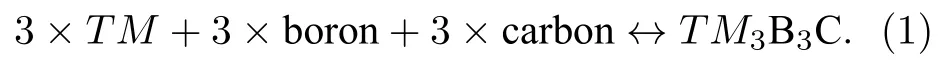
对于该化学反应,可以通过下式来判断化学反应的方向：

式中,ΔHelements是三种单质生成TM3B3C化合物的形成焓;HTM3B3C,HTM,Hboron和Hcarbon分别是三元TM3B3C、单质TM、单质硼以及石墨的焓值(单位：eV/atom).如果 ΔHelements＞0 ,则意味着化学反应向左进行,三元相TM3B3C是不稳定的,意味着容易相分离;否则就说明化学反应可以向右进行,三元TM3B3C相对其三种单质材料来说是稳定的.形成焓的计算结果列于表2中,相对于单质而言,有16种TM3B3C相是不稳定的,首先被排除.剩下的13种TM3B3C相倾向于不分解,集中于第IIIB—VIIB族(Re除外)过渡金属元素.但是这13种相对单质的稳定相,还可能分解为单质、二元相以及三元相的任意组合.因此对每种TM-B-C组分,通过在无机晶体结构数据库(ICSD)和美国材料基因组计划所建的材料数据库(materials project网站)[23]搜索其相应的各种单质、二元相和三元相,任意组合形成TM3B3C组分.在各种任意组合中,焓值总和最低的那一组称之为TM3B3C相的最稳定竞争组合.采用如下公式计算这13种相对单质稳定TM3B3C相的热力学稳定性：

式中,ΔHcomp是最稳定竞争组合生成TM3B3C化合物的形成焓,Hcomp是最稳定竞争组合的焓值(单位：eV/atom).如果 ΔHcomp＞0 ,则意味着三元相TM3B3C是不稳定的,会分解成最稳定竞争组合;否则就说明相对所有可能分解产物,三元TM3B3C化合物都能稳定存在.形成焓 ΔHcomp计算结果列于表2中,每种成分TM3B3C的最稳定竞争组合也列于表2中.从表2可以看出,热力学稳定的TM3B3C相只有Nb3B3C一种,这和实验上已经合成了Nb3B3C相[17]的结果是一致的,也说明了本文计算结果的准确性和可靠性.但同时注意到,Ta3B3C相的形成焓 ΔHcomp虽为正值,但和最稳定竞争组合的焓差只有0.003 eV/atom.密度泛函理论第一性原理只能计算绝对零度下材料的结构和性能,因此如果考虑温度因素,形成能完全有可能变成负值.采用准谐近似方法[22,24]计算了0—2000 K下Ta3B3C相及其最稳定竞争组合相的自由能,如图2所示.当温度超过约250 K后,Ta3B3C相的自由能开始低于其最稳定竞争组合相,因此采用现代材料合成方法,Ta3B3C相是完全可以在高温下合成得到.

表2 不同成分TM3B3C和TM4B3C2的形成焓(eV/atom)Table 2.Calculated formation enthalpies of differentTM3B3C andTM4B3C2phases (eV/atom).

图2 不同温度下Ta3B3C,Ta4B3C2相分别和其相应最稳定竞争组合相的自由能之差Fig.2.Energy differences of Ta3B3C and Ta4B3C2phases with respect to their most competing phases as a function of temperature.

采用上述类似方法,也计算了29种TM4B3C2相的形成焓,结果见表2.相对于单质,有18种TM4B3C2相倾向于分解,只有11种TM4B3C2相对于单质可以稳定存在,集中于第IIIB—VIB族过渡金属元素.但相对于最稳定竞争组合,只有Nb4B3C2和Ta4B3C2是热力学稳定的.图2显示Ta4B3C2相在整个高温区间(0—2000 K)都可以稳定存在.相对Ta3B3C相来说,Ta4B3C2相与其相应最稳定竞争相组合的焓差更大,因此意味着Ta4B3C2相要比Ta3B3C相具有更好的稳定性.

通过以上计算,本文成功预测了Ta3B3C和Ta4B3C2两相可以热力学稳定存在.本文的预测是基于Nb3B3C和Nb4B3C2结构进行的,因此所得的Ta3B3C和Ta4B3C2两相均为这两种结构.对于Ta3B3C和Ta4B3C2组分而言,有可能会存在能量更低的更稳定结构.基于遗传算法的USPEX软件[18]和基于粒子群优化算法的CALYPSO软件[19]是当前流行的结构预测软件,在结构预测领域已经有了很多成功的先例.为了确保结果的可靠性,采用这两种预测软件搜索全局最稳定结构.采用USPEX和CALYPSO建立候选结构,每一代生成50个结构,结构优化由VASP软件来完成,如果每一代能量最低结构连续20代保持不变,则认为结构搜索收敛,找到了全局能量最低结构.两种软件的计算搜索结果都显示基于Nb3B3C和Nb4B3C2的Ta3B3C和Ta4B3C2结构均为能量最低结构,从而确定了Nb3B3C和Nb4B3C2型结构为Ta3B3C和Ta4B3C2组分的基态结构.其结构信息列于表1中,由于Ta—B和Ta—C的键长分别稍短于Nb—B和Nb—C的键长,使得Ta3B3C和Ta4B3C2的晶格参数稍小于相应的Nb3B3C和Nb4B3C2的数值.

3.2 动力学和力学稳定性

为了验证Ta3B3C和Ta4B3C2结构的动力学稳定性,计算了其声子色散曲线,绘制于图3中.在整个布里渊区范围内均未见任何虚频,这表明这两个结构在动力学上是稳定的.

力学稳定性是材料存在的另一个必要条件.力学稳定性意味着晶体在发生形变时,应变能为正值.力学稳定性可以通过检验弹性常数是否满足特定的条件来判断[25].对于Ta3B3C和Ta4B3C2所属的正交晶系,稳定结构的9个独立弹性常数需满足如下条件：C11＞ 0,C44＞ 0,C55＞ 0,C66＞ 0,,C11C22C33+2C12C13C23---＞0 .计算的Ta3B3C和Ta4B3C2结构弹性常数列于表3中,可见都符合上述条件,因此Ta3B3C和Ta4B3C2结构都是力学稳定的.

3.3 力学性能

多晶材料的弹性模量可以由单晶体的弹性常数计算得到.体弹模量B和剪切模量G可分别由以下公式得到[26]：

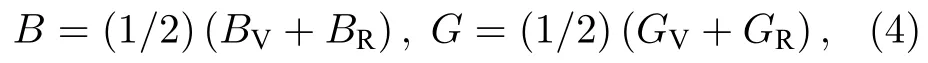
其中,下标V和R分别代表Voigt和Reuss方法.

BV,BR,GV和GR可由以下公式得到：

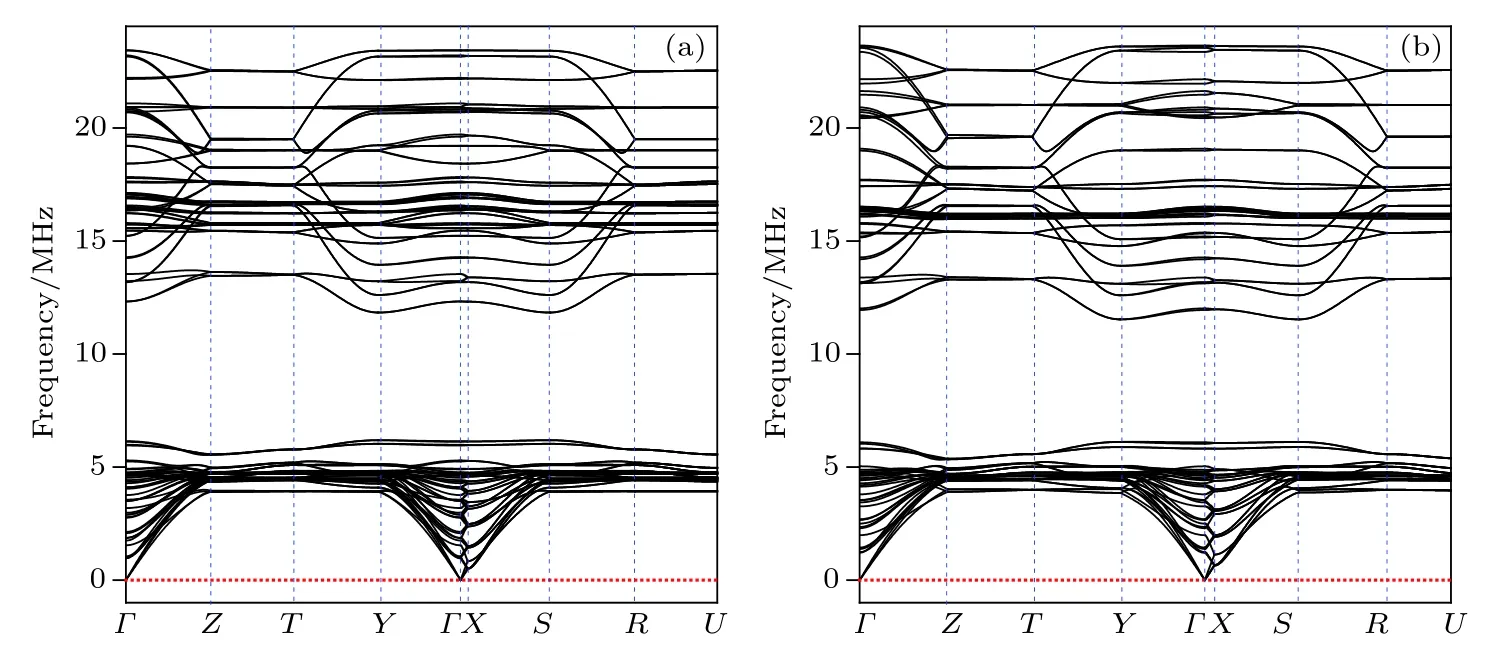
图3 (a) Ta3B3C和(b) Ta4B3C2结构的声子色散曲线Fig.3.Phonon dispersion curves of (a) Ta3B3C and (b) Ta4B3C2structures.

其中,Δ=C13(C12C23-C13C22)+C23(C12C13-C23C11)+C33(C11C22-).

Ta3B3C和Ta4B3C2结构的体弹模量B和剪切模量G见表3.为了比较,Nb3B3C和Nb4B3C2结构的计算数据也一并给出.对同一成分来说,TM4B3C2结构的B和G值均稍大于TM3B3C结构;对不同成分来说,Ta3B3C (Ta4B3C2)结构的B和G值均稍大于Nb3B3C (Nb4B3C2)结构,这源于Ta-B-C中稍短的键长,这说明新发现的Ta-BC相抵抗弹性变形的能力要强于相应的已知Nb-B-C相.根据Pugh经验判据[27],B/G的比值可用来判断一个材料是脆性还是韧性.若B/G＞ 1.75,表明材料是韧性的;反之表明材料是脆性的.根据这个判据可知,Ta3B3C,Ta4B3C2结构和已知的超硬或者硬质材料相同,属于脆性材料.

为了探索Ta3B3C和Ta4B3C2相作为硬质材料的可行性,计算了其硬度.计算方法采用中国科学院金属研究所陈星秋公式[28]和燕山大学田永君公式[1]：

(6)和(7)式中,HChen和HTian是分别根据陈星秋和田永君硬度公式计算得到的维氏硬度,k为剪切模量G和体弹模量B的比值.

计算的Ta3B3C,Ta4B3C2,Nb3B3C,Nb4B3C2结构以及一些已知二元相的硬度值列于表3中.两种硬度计算方法的结果很相近,都显示本文新发现的Ta-B-C三元相硬度约为26 GPa,稍高于已知Nb-B-C三元相.26 GPa的硬度值表明Ta3B3C和Ta4B3C2相都不是超硬材料,但也属于高硬度材料.其硬度值和相应的二元相TaB2,TaC相近,高于Al2O3和TiN材料,但低于SiC材料.

3.4 电学性能

图4 (a),(c) Ta3B3C和(b),(d) Ta4B3C2结构的能带结构和态密度图Fig.4.Band structures and density of states of (a),(c) Ta3B3C and (b),(d) Ta4B3C2structures.

图4给出了Ta3B3C和Ta4B3C2结构的能带结构和态密度(DOS)图.能带结构图中,费米面横穿过能带,导带和价带互相交叠,这说明两相均为导体.从DOS图可以看出,费米面上的电子态主要是Ta原子的d电子,因此其导电性主要源于Ta原子的d电子.由于这两相具有类似的结构,因此其态密度图很相似.其价带部分可以看成由9个电子态峰组成,除了峰2和峰3为Ta原子和B原子的电子贡献以外,其他7个电子态峰均含有三种原子的电子.对B原子和C原子来说,从—14 eV到—10 eV的峰1,主要来源于2s轨道上的电子,而—10 eV到费米能级的能带区域则主要来源于2p电子.从—10 eV到费米能级的能带区域看,Ta原子的d电子与B原子的p电子,以及Ta原子的d电子与C原子的p电子之间均发生了较强的杂化,这说明Ta和B以及Ta和C之间是很强的共价结合.

4 结 论

本文基于密度泛函理论第一性原理计算方法,以Nb3B3C和Nb4B3C2结构为模板,采用元素替代法和结构搜索法相结合,成功预测了两种稳定的Ta3B3C和Ta4B3C2新相.其中Ta3B3C结构虽不是绝对零度下的基态稳定相,但高温下可以稳定存在.Ta3B3C和Ta4B3C2新相的维氏硬度大约为26 GPa,表明这两相虽没有达到超硬材料的标准,但也属于高硬度材料.这两相还是导电的脆性材料.另外其他诸如光学、热学等性能期待后续的挖掘和研究.相对二元相,三元相具有更大范围的成分以及性能可调性,因此我们期待Ta3B3C和Ta4B3C2相是新型可调多功能硬质材料.同时本文的研究思路和计算方法,后续可以扩展到更多已知材料体系,从而可以预测甚至合成更多的稳定新相.