线极化Bell-Bloom测磁系统中抽运光对磁场灵敏度的影响*

杨晨 左冠华 田壮壮 张玉驰 张天才‡

1) (山西大学光电研究所,量子光学与光量子器件国家重点实验室,极端光学协同创新中心,太原 030006)

2) (山西大学物理电子工程学院,太原 030006)

利用适用于线极化Bell-Bloom测磁系统的布洛赫方程和含有自旋弛豫的速率方程,以铯原子为研究对象,分析了抽运光对磁场灵敏度的影响,并在实验上分别采用与铯原子D1线和D2线共振的线偏光作为抽运光和探测光,用充有缓冲气体的气室进行了实验.实验结果与理论分析一致,均表明只有在一定的光强范围内,增大抽运光光强可以提高磁场灵敏度.且利用这一方法分析了原子的自旋弛豫对磁场灵敏度的影响.这项研究对于深入认识线极化的Bell-Bloom测磁系统,以及如何通过优化系统实现磁场灵敏度的提高具有重要的意义.

1 引 言

磁场精密测量在矿产勘探、医学探测和精密测量物理等方面具有广泛的应用[1].近几年来,随着人们对光与原子相互作用的进一步认识,国内外已经开展了大量利用原子自旋系统对磁场测量的研究.目前,国际上灵敏度最高的磁强计是利用原子的无自旋交换弛豫(spin-exchange relaxation free,SERF)过程[2]实现的,即SERF态,其灵敏度可以达到[3],但将原子制备到SERF态需要满足特定的条件,而且其只能测量近零磁场,在实际应用中受到很大的限制.

Bell和Bloom[4,5]在20世纪60年代就提出,利用振幅调制的光场与磁场中的原子相互作用,当调制频率ωm等于原子极化在磁场中的进动频率时,即可实现磁共振.抽运光为圆偏光时,原子极化的进动频率等于拉莫尔进动频率ωL[5-7];当抽运光为线偏光时,原子极化的进动频率为拉莫尔进动频率的两倍[4,8-10].利用原子的磁共振现象,可以实现对非零磁场的测量.当抽运光为线偏光时,磁场灵敏度 δB可表示为[11]

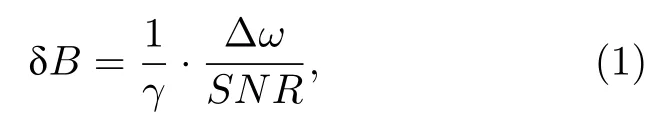
其中γ为旋磁比,对于铯原子γ= 2π×3.5GHz/T ;Δω为磁共振线宽,即磁共振谱线的半高半宽;SNR为磁共振(ωm=2ωL)时的信噪比.

Bell-Bloom结构的测磁系统[11-15]目前已可以实现对μT量级[16],以至地磁环境下[17]的磁场测量,可得到的最高的磁场灵敏度为[16],是一种重要的测量磁场的方法.

由(1)式确定的磁场灵敏度取决于磁共振线宽和磁共振时的信噪比.2004年,Julsgaard等[18]指出磁共振线宽不仅取决于原子自旋弛豫率的大小,还与抽运光有关.在一定的噪声环境下,磁共振时的信噪比取决于原子的极化程度,即原子在基态各个磁子能级布居数的差异.早在1987年,Avila等[19]就用含有光抽运过程和自发辐射的速率方程分析了不同抽运频率和偏振对原子基态布居数的影响.

原子极化在磁场中进动时,光抽运过程和原子自旋弛豫对原子极化的影响可用布洛赫方程[20,21]描述.因此,若在速率方程中引入原子的自旋弛豫,结合布洛赫方程,即可深入分析抽运光对磁场灵敏度的影响.

本文以刘维尔方程[15,22,23]为基础,建立含有原子自旋弛豫的速率方程.将速率方程与线极化时原子的布洛赫方程相结合,以铯原子为研究对象,对线偏振的抽运光的频率分别对应直接抽运(D1线62S1/2F=4 — 62P1/2F′=3 )与间接抽运(D1线62S1/2F=3 — 62P1/2F′=4 )时,抽运光光强对磁场灵敏度的影响进行了分析.与此同时,利用与D2线共振的线偏光作为探测光,以充有缓冲气体的铯原子气室为实验对象,通过在不同抽运频率下改变抽运光的光强,对磁场灵敏度进行测量.实验结果与理论分析一致.

本文首先介绍了Bell-Bloom结构测量磁场的基本原理,并建立含自旋弛豫的速率方程;然后,介绍了实验装置及实验结果;最后,对结果进行了分析和讨论.

2 理论分析

2.1 Bell-Bloom测磁系统的原理

图1为线极化的Bell-Bloom测磁系统基本原理图.抽运光振幅调制的频率为ωm,偏振沿z轴方向,使原子在无磁场时的极化方向为z.磁场B沿x轴方向,使得原子在yoz平面内进动.探测光的偏振方向为y,可以实现对原子极化沿着y轴方向的探测.若原子的自旋弛豫率为r0,光场的调制频率为ωm,且光强在0—2I0变化,当探测光很弱时(远低于其饱和光强)其抽运效应可以忽略,在旋转坐标系下,原子极化P在磁场中随时间t演化的布洛赫方程[24]应表示为

其中α为抽运速率与光强的比值.当抽运光频率ω固定时,α为定值.当抽运光频率与原子共振时(即如图2(a)中所示,ω=ω0时),α有最大值.

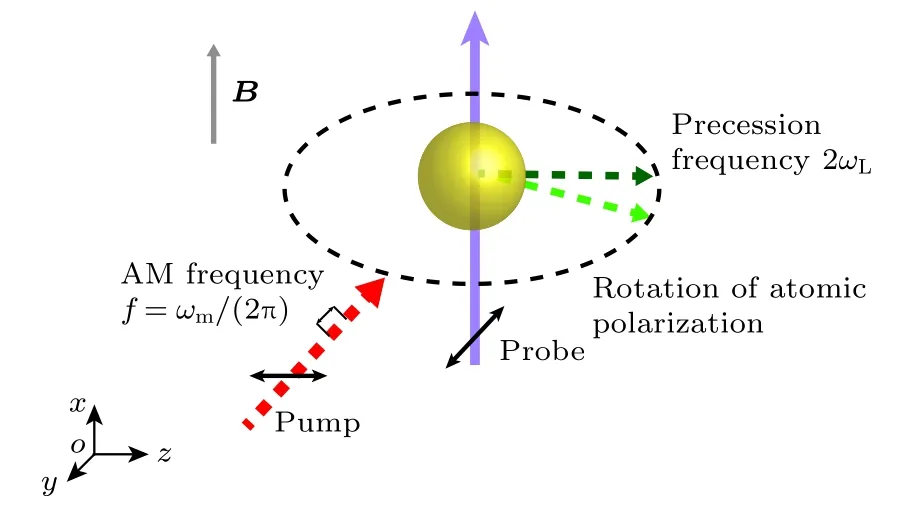
图1 线极化的Bell-Bloom测磁系统基本原理图Fig.1.Bell-Bloom configuration with linearly polarized pump beam.

由图1可以看出,当探测光为偏振沿y轴方向的线偏光时,则可探测原子极化沿着y轴方向的分量Py.若抽运光光强I0为定值,用锁相探测的办法,对调制频率不同时Py的同相信号Py(in) 进行探测,即可得到磁共振谱线：

对于同类课程的积极引导意义和借鉴作用在于：开发了紧密围绕护理职业岗位要求和护士职业标准的课程内容；课程组成员与医院合作开发了以任务为载体、以项目为导向的课程教材；实施了校院结合、教学做一体化教学模式。

由(4)式可知,磁共振谱线具有洛伦兹线型,其半高半宽即为原子的磁共振线宽：

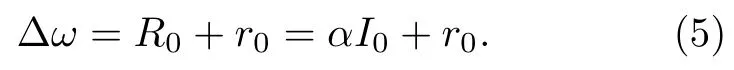
磁共振(ωm=2ωL)时,(4)式的信号有最大值：

由(6)式可知,若固定探测光的光强,则探测信号在磁共振时的SNR与原子极化P0成正比.以铯原子为例,若探测光与基态 62S1/2F=4 的原子共振,则P0取决于该基态各个磁子能级的粒子数分布.

2.2 含自旋弛豫的速率方程

抽运光与原子相互作用,导致原子在基态各个磁子能级上分布不均匀,由此可以实现原子的极化.这一过程可以用速率方程[25]来描述.

如图2(a)所示,铯原子D1线基态与激发态之间的拉比振荡频率为ΩR,|a〉和|c〉表示基态的两个磁子能级,|b〉为激发态的一个磁子能级.抽运光与原子共振,频率为ω0,即|a〉与|b〉之间的频率差.在抽运光的作用下,原子由|a〉跃迁至|b〉.若|b〉的自发辐射率为Γ0,|a〉与|b〉之间的偶极矩阵元为η,|c〉与|b〉之间的偶极矩阵元为θ,则原子由|b〉自发辐射至|a〉和|c〉的速率分别为η2Γ0和θ2Γ0.

原子密度矩阵随时间t的演化可以用刘维尔方程[23]描述：

(7)式右侧第一项表示光与原子之间的相互作用,第二项和第三项分别表示由于|b〉的自发辐射和基态的自旋弛豫引起的各个磁子能级布局数的减小和增加.其中

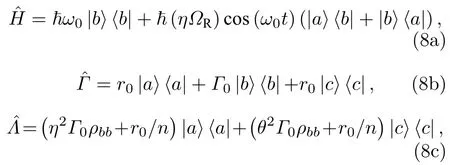
其中 ℏ 为约化普朗克常数;n为基态磁子能级的总数,对于铯原子n= 16 .

图2 抽运光与铯原子相互作用 (a)光与铯原子相互作用;(b)线偏振的抽运光与铯原子相互作用Fig.2.Interaction between pump light and cesium atoms：(a) Light-atom interaction;(b) interaction between linearly polarized pump light and cesium atoms.

利用(9a)—(9c)式,可以得出直接抽运(对应62S1/2F=4 — 62P1/2F′=3的跃迁)及间接抽运(对应 62S1/2F=3 — 62P1/2F′=4 的跃迁)时,各个基态磁子能级布居数随时间t的变化,在特定参数下的数值计算结果见图3,其中β=(2π)2×7×109(Hz)2×m2/W,Γ0=2π×4.5MHz,r0=2π×60Hz.当I0=0.5W/m2时,直接抽运的情况 如图3(a)所示,原子在 62S1/2F=3 各个磁子能级的布居数之和为0.59;在基态 62S1/2F=4 的磁子能级mF=4和mF=-4 的布居数之和为0.21,占到原子该基态总布居数的51%.当I0=10W/m2时,间接抽运的情况如图3(b)所示,最终原子在62S1/2F=3 各个磁子能级的布居数之和为0.015,原子在 62S1/2F=4 各个磁子能级上布居数分别为0.069(mF=±4),0.097(mF=±3),0.120(mF=±2),0.136(mF=±1)和0.141(mF=0 ).

若用基态 62S1/2F=4两个磁子能级mF=4与mF=0之间的粒子数差 ΔN表示原子的极化P0,由(6)式可知,磁共振时的信号幅值为

若探测光的光强保持不变,利用(1)式,可定义与δB呈正相关的约化磁场灵敏度：

直接抽运与间接抽运时,磁共振时的信号幅值与约化磁场灵敏度 δB0随抽运光光强I0的变化趋势如图4所示.从图4可以看出,直接抽运(图4(a))与间接抽运(图4(b))时,约化磁场灵敏度随抽运光光强的变化均呈先减小后增大的趋势.

3 实验系统与结果

在实验上搭建了抽运光和探测光均为线偏光的原子测磁系统,如图5所示.

图3 铯原子基态 62S1/2F=4和 62S1/2F=3各个磁子能级的布居数随时间的演化 (a)I0=0.5W/m2 时,直接抽运的情况;(b)I0=10W/m2 时,间接抽运的情况Fig.3.Evolution of the populations in each Zeeman sublevels with time of cesium atoms’s ground state 62S1/2F=4 and 62S1/2F=3：(a) Results of direct pump with the pump intensityI0=0.5W/m2 ;(b) results of indirect pump with the pump intensityI0=10W/m2 .

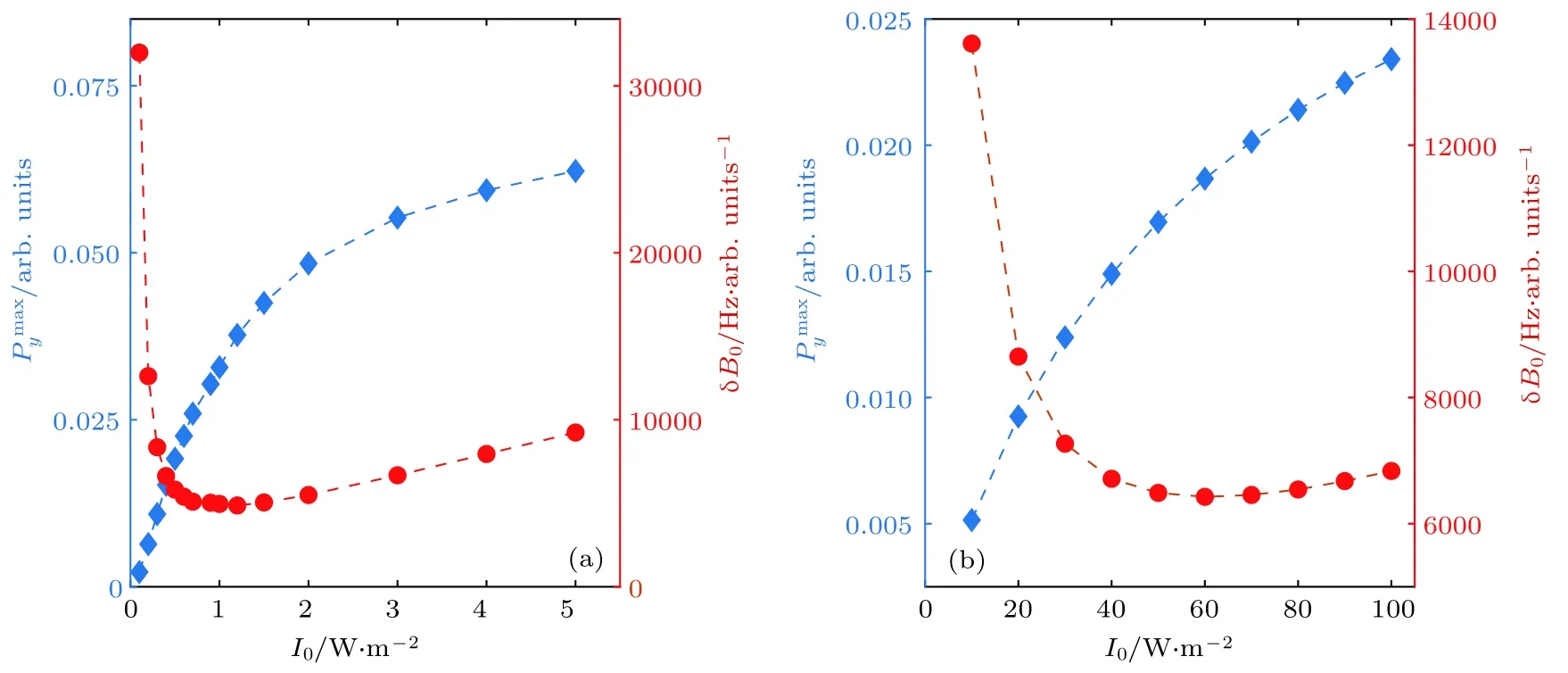
图4 磁共振时,信号幅度与约化磁场灵敏度 δB0随抽运光光强I0的变化 (a)直接抽运,α = 2π×103Hz×m2/W ;(b)间接抽运,α=2π×1Hz×m2/WFig.4.Signal amplitude and relative sensitivity δB0change along with the pump intensityI0under the condition of magnetic resonance：(a) Direct pump withα = 2π×103Hz×m2/W;(b) indirect pump withα = 2π×1Hz×m2/W .

实验系统包括如下四个部分.第一,原子气室部分：所用的铯原子气室为20 mm × 20 mm × 20 mm的立方形气室,并在气室中充入约20 Torr(1 Torr ≈ 133.322 Pa)的氦气作为缓冲气体.待测磁场沿着x轴方向,由一对亥姆霍兹线圈(HC)产生.上述装置全部置于磁屏蔽筒(magnetic shield)中.第二,激光系统部分：抽运光和探测光的偏振分别沿着z轴方向和y轴方向.抽运光的频率锁定在铯原子D1线,并用一个连续可变衰减(VNDF)调节光强.探测光频率锁定在铯原子D2线 62S1/2F= 4— 62P3/2F′=5 的跃迁线,光强为 0.2W/m2(约为饱和光强的1%).第三,探测部分：探测光经过气室后,经渥拉斯顿棱镜(WP)分束,用平衡探测器(BPD)[26]对其偏振变化进行探测.将探测到的偏振信号作为锁相放大器(LIA,型号SRS SR830)的信号输入(Sig in)进行处理,或直接用频谱分析仪(SA,型号SRS SR770)对信噪比进行测量.第四,信号处理与测量部分：交流信号源(AC,型号SRS DS345)的频率为ωm,将其作为锁相放大器的参考输入(Ref in),同时将锁相放大器的参考输出(Ref out)用于驱动抽运光光路中的电光振幅调制器(EO-AM,型号Thorlabs EOAM-NR-C1).当交流信号源的频率在磁共振频率( 2ωL)附近扫描时,锁相放大器的信号输出(Sig out)即为磁共振谱线.当交流信号源的频率固定在磁共振频率时,用频谱分析仪对共振频率处的信噪比进行测量,结合(1)式,即可得出磁场灵敏度 δB.

固定抽运光的光强I0,直接抽运和间接抽运得到的磁共振谱线如图6所示.磁共振谱线符合洛伦兹线型,通过洛伦兹拟合可以确定半高半宽,即磁共振线宽 Δω.扫描抽运光的振幅调制频率ωm,对锁相放大器的同相输出信号进行测量可以得到磁共振谱线.谱线可以用(4)式给定的洛伦兹线型进行拟合,图中的实线为实验数据,虚线为拟合曲线.拟合曲线的中心对应磁共振频率 2ωL,可知此时磁场大小约为3.4 μT.图中绿色实线与黑色虚线是直接抽运且抽运光光强为 0.4W/m2时的结果,拟合出的磁共振线宽为 2 π×(113.5±0.1)Hz .图中红色实线与蓝色虚线是间接抽运且抽运光光强为1.0W/m2时的结果,拟合出的磁共振线宽为2π×(72.94±0.22) Hz.

图6 直接抽运与间接抽运的磁共振谱线Fig.6.Spectra of magnetic resonance with direct pump and indirect pump.

在不同光功率下对磁共振谱线进行测量,可以得到磁共振线宽 Δω随抽运光光强I0的变化,结果如图7所示,图中的蓝色圆点均为实验数据点,数据点和误差棒均为五次测量结果,红色实线为利用(5)式拟合的结果.由图7可知,间接抽运时的α远小于直接抽运的结果,这是由于间接抽运时,抽运光相对于基态 62S1/2F=4 为远失谐.

图8为磁共振时,信噪比SNR及磁场灵敏度δB随抽运光光强I0的变化,图中的数据点和误差棒来自五次测量的结果.图8(a)为直接抽运的结果,可达到的最高的磁场灵敏度为;图8(b)为间接抽运的结果,可达到的最高的磁场灵敏度为.与图4的结果类似,在直接抽运与间接抽运时,随着抽运光光强的增大,磁场灵敏度均呈先减小后增大的趋势.由此可见,只有在一定的光强范围内,增大抽运光光强可以提高磁场灵敏度.结合图7和图8可知,间接抽运时,α值较小,且改变抽运光光强,可达到的信噪比远大于直接抽运的结果,因此间接抽运可以得到更高的磁场灵敏度.

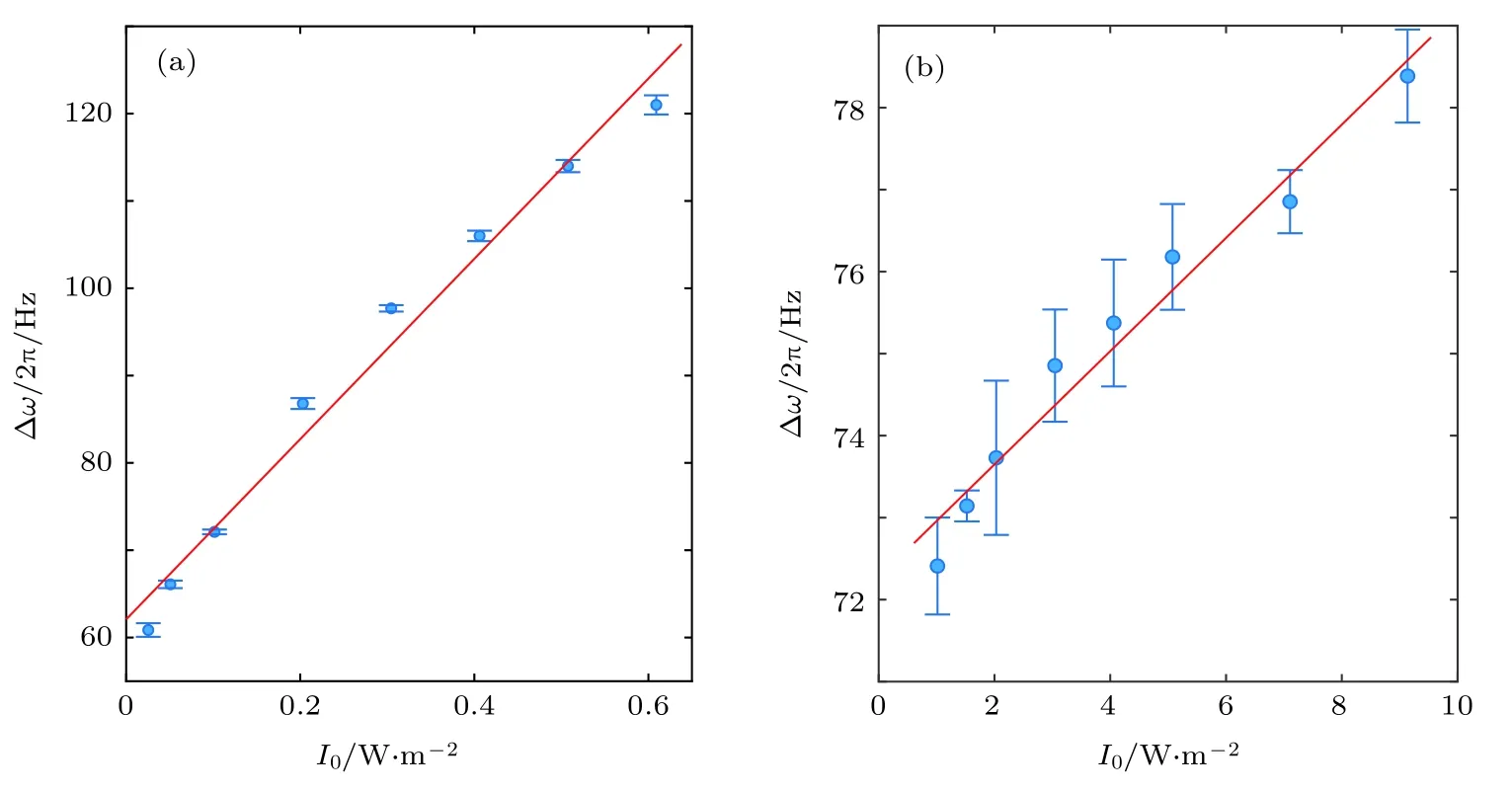
图7 磁共振线宽 Δω随抽运光光强I0的变化 (a)直接抽运,α = 2π×(103.2±14.3)Hz×m2/W;(b)间接抽运,α=2π×(0.6907±0.1318)Hz×m2/WFig.7.Variation of magnetic resonance linewidth Δωwith pump intensityI0：(a) Direct pump,α=2π×(103.2±14.3)Hz×m2W;(b) indirect pump,α = 2π×(0.6907±0.1318)Hz×m2 /W.

图8 磁共振时,信噪比SNR与磁场灵敏度 δB随抽运光光强I0的变化 (a)直接抽运;(b)间接抽运Fig.8.Variation of SNR and sensitivity δBwith the pump intensityI0under the condition of magnetic resonance：(a) Direct pump;(b) indirect pump.

4 分析与讨论

以上实验结果说明,由理论分析得出的磁场灵敏度的变化趋势与实验结果基本一致.因此,可以利用相同的办法,对自旋弛豫率r0不同时,磁场灵敏度随抽运光光强的变化进行系统的分析.

图9为抽运光频率对应间接抽运,且自旋弛豫率r0不同时,约化磁场灵敏度 δB0((11)式)随抽运光光强I0的变化,图中参数除r0以外,均与图4相同.由图9可知,随着自旋弛豫率的增大,系统达到最高的磁场灵敏度需要更大的抽运光光强.当抽运光光强固定时,随着自旋弛豫率的增大,磁场灵敏度降低.由此可见,可以在不减弱抽运光与原子之间的相互作用(即不减小α和β)的情况下,通过在气室内壁镀抗弛豫膜[27-29],或增大磁场的均匀区[30,31]等手段来减小自旋弛豫率,以提高磁场灵敏度.

图9 在自旋弛豫率r0不同时,间接抽运的约化磁场灵敏度δB0随抽运光光强I0的变化Fig.9.sensitivity δB0and pump intensityI0with indirect pump under the condition of different relaxation rater0.

5 总 结

本文利用磁场中原子的布洛赫方程及含有自旋弛豫的速率方程,以铯原子为例,分析了当线偏振的抽运光分别为直接抽运(对应D1线62S1/2F=4—62P1/2F′=3 的跃迁)和间接抽运(对应D1线 62S1/2F=3—62P1/2F′=4 的跃迁)时的磁共振线宽、磁共振时的信噪比及磁场灵敏度随抽运光光强的变化.将与铯原子D2线62S1/2F=4 — 62P3/2F′=5 的跃迁共振且光强远小于铯原子饱和光强的线偏光作为探测光,利用充有20 Torr氦气作为缓冲气体的铯原子气室进行实验,得到的实验结果与理论分析一致.本文还利用相同的理论分析了原子的自旋弛豫对磁场灵敏度的影响.这项研究对于我们进一步的认识线极化Bell-Bloom测磁系统中的动力学过程具有重要的意义,并为通过优化原子气室参数[32],或结合使用弱测量[33,34]及非破坏性测量[35,36]等手段进一步提高磁场灵敏度提供了可能.