集群航天器球形边界控制

陈严波，韩笑冬，姜 斌，程月华

0 引 言

通常将由多颗近距离伴飞的卫星协同完成任务的系统称为集群航天器.集群航天器是继星座以及编队的发展之后，逐渐兴起的一种分布式系统[1].传统航天器多采用复杂的集中式架构,具有较长的研制周期，维护较为困难[2].集群航天器继承了航天器编队飞行的优势，与此同时，又具有生物集群的特性，因此集群航天器具有更灵活、更快的响应速度、更好的容错性等优点，因此在具有不确性的空间环境中可以执行许多复杂的科研任务.

目前，针对集群航天器的一致性问题、集群构型等的研究，已经取得了较多的研究成果.一致性控制[3]为集群航天器相对构型的设计提供了理论基础.蜂拥控制[4]通过建立简单的行为准则，使得集群航天器可以在避免碰撞的前提下保持松散的构型.带领航反馈[5]的蜂拥控制算法可以使得集群跟随领航星运动，并且可以保证基于局部通讯方式的集群中，每一个航天器的速度最终都能趋于一致.对于航天器数目较多的集群来说，全局通讯通常需要花费的代价是十分巨大的，例如功耗的增加、信息延时变长，节点的网络负担加重.同时相关研究结果表明，即使简单的相对简单的模型，当智能体间存在更多的通信时，不一定能取得更快的系统收敛速度，相反还有可能影响系统的收敛性[6].

对于集群航天器来说，希望集群在蜂拥控制的作用下稳定时，可以对集群边界(所有航天器的包络面)的尺度进行控制，将航天器约束或分散在给定的空间范围内.有关集群边界控制的研究较少，而对于集群构型的研究则较多，有文献通过一致性算法来维持集群特定的构型[7-9]，但是这种构型通常较为严格，不符合集群松散队形的要求；还有文献通过椭圆空腔虚拟势场[10]的方法，将集群限制在椭圆形的边界上，这种集群控制方法保证了集群在边界上松散分布，但是造成了椭圆形边界内部出现“空洞”的现象，即集群内部边界以内不存在个体.文献[11]中使用轨迹跟踪误差设计出相应的控制率来实现无人机群的编队控制，但这种控制方法对个体数目较多的集群来说难以实现.文献[12]提出了航天器群运动过程中的边界问题，但该航天器群并非集群航天器的概念，而且该文中边界的概念与本文所提的边界也不相同.文献[13]中设计出一种新颖的开环纳什控制策略，使无人机群通过完全分布式的方式估计出其终端状态，从而实现了无人机群的编队控制.但这种控制策略要求具有固定的编队的构型.

基于局部通讯，集群航天器边界控制的意义在于：集群边界的改变同时改变了通讯链路的数量，无任务时可以通过增大集群边界使得航天器之间的通讯链路减少来减小能耗；当集群航天器需要绕过空间障碍区时，对集群边界的控制可以使集群顺利通过(即整体避障).若集群包络面可以通过，则只需规划虚拟领航星的轨道即可使得集群顺利通过；若集群包络面无法通过，则可以通过缩小集群边界，使得集群包络能够通过障碍区.如图1所示.

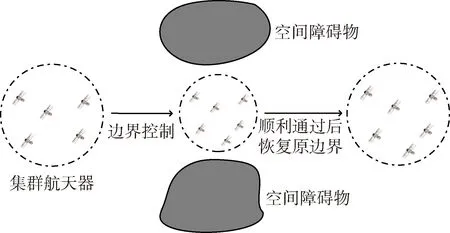
图1 集群整体避障Fig.1 Obstacle avoidance of spacecraft cluster

本文设计的集群航天器边界控制系统如图2所示，其中集群航天器动力学模型的输出为各航天器的位置、速度；蜂拥控制器作用于每个航天器个体，用于实现集群的速度一致性(使得集群内部相对位置稳定)以及避免集群内部的碰撞；动力学模型的输出通过粒子群球形边界搜索模块得到球形边界中心(xc,yc,zc)以及半径Rc；势函数边界控制器根据集群的边界反馈信息，仅对处于集群边界附近的航天器产生球形空腔势场力，从而使得集群边界达到期望值.

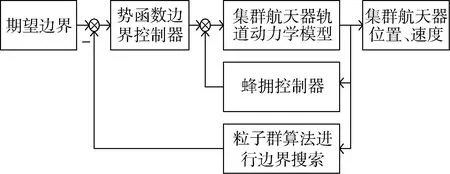
图2 集群航天器边界控制系统框图Fig.2 Boundary control system of cluster spacecraft

1 集群航天器蜂拥控制问题

为了描述航天器间的相对运动，从而可以较为直观地反映出航天器间相对位置地变化，这里引入参考轨道坐标系Oc-xcyczc,坐标原点位于参考星的质心.xc轴由地心指向参考星质心，zc轴指向参考星轨道面法线方向，Oc-xcyczc构成右手直角坐标系，如图3所示.

图3 参考轨道坐标系Fig.3 Coordinate system of reference orbit

当参考轨道为圆轨道，且航天器相对参考星距离较近时，航天器相对于参考星的运动可由C-W方程描述：

(1)

(ux,uy,uz)为其他力在参考轨道系下产生的加速度输入，w0为参考星角速度.

基于C-W方程，航天器i的控制输入形式如下：

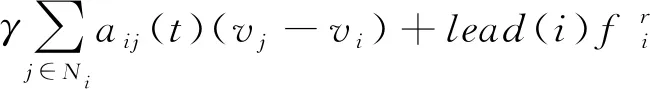
(2)

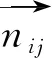
参考文献[14]，取如下的势场作用力函数:

(3)

其中，r为航天器之间的距离，k1为引力系数，k2为斥力系数，rmax为航天器间的最大通讯距离，则当作用力为零时，达到平衡状态，有：

(4)

其中re为期望保持的距离.当lead(i)=1时，领航反馈项可以按一致性理论中的形式给出：

(5)

其中rr、vr分别为领航星的位置、速度矢量，α1、α2分别为领航星位置、速度反馈系数.当集群中所有的航天器都能感知到领航星的状态信息时，对于任意初始状态，集群航天器最终可以实现一致性.在集群航天器速度达成一致性时，航天器之间相对位置保持不变(稳态).因此可以在集群航天器处于稳态时研究集群的边界，并根据其边界信息设计边界控制方法.

2 集群航天器边界研究

集群航天器蜂拥控制是进行边界控制的基础，只有当航天器之间的相对距离保持稳定，边界控制才有意义.为了实现集群航天器的边界控制，首先对边界进行定义，再研究合适的搜索算法得到集群的边界，以此为反馈信息，实现边界控制.2.1中给出集群球形边界以及盒形边界的两种定义，2.2中使用粒子群算法对2.1中最小球形边界进行寻优，并结合仿真进行了验证.

2.1 集群边界定义

集群边界指的是包含所有个体的具有最小尺寸的包络面，定义并不唯一，通常根据不同的需求来给出不同的定义，通常有两种定义，球形边界和盒形边界.球形边界更容易求解，但对于一些特殊分布的集群拟合效果并不好；盒形边界比球形边界的拟合效果好，但通常不易求解.

1)球形边界

球形边界指的是包络集群中所有个体的最小半径的包络球.集群半径最小包络球的确定主要存在两个问题，首先是包络球球心的确定，其次是包络球半径的确定.事实上，集群的包络球的中心也是随集群整体运动而运动的，因此可将其视为一颗虚拟的卫星集群在参考轨道坐标系下相对位置稳定时，即代表集群的构型保持不变，因此可以对集群边界进行建模(球形)ri为航天器i位置矢量，r0为球心位置矢量，得到最小的包络球的半径Rmin为：

(6)

上述函数自变量为球心位置r0，由于上述表达无法直接最值，因此需要用到智能搜索算法来求得近似解，这里我们使用粒子群算法找到最优的r0.图4为集群球形边界示意图.

图4 球形边界Fig.4 Spherical boundary

2)盒形边界

盒形边界顾名思义，就是长方体形状的集群边界，如图5所示.

图5 盒形边界Fig.5 Box boundary

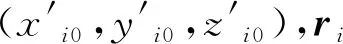
基于不同的性能指标，盒形边界有不同的形式，基于盒形长宽高最大尺寸的最小值的性能指标，有：

(7)

基于盒体积最小的性能指标，有：

(8)

2.2 基于粒子群算法的集群球形边界寻优

1)粒子群搜索算法设计

在本文的球形边界寻优问题中，性能指标函数如式(6)，每个粒子的位置为x，即代表球形边界的球心坐标r0的一个可行解.每个粒子的速度、位置更新如下所示：

(9)

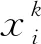
2)集群航天器边界寻找过程仿真

设置参考星轨道为圆轨道，轨道高度500 km，集群由10颗星组成，初始位置随机分布距离参考星(-3 km，3 km).通过蜂拥控制，使得集群稳定时寻找集群球形边界.

图7中为蜂拥控制在稳态时，航天器间的相对位置、通讯拓扑以及球形边界.蓝色五角星表示航天器，航天器之间的连线代表它们的通讯拓扑，圆形阴影代表球边界的半径.从图7可以看出，航天器间通过局部通讯，在蜂拥控制作用下，集群稳态时并没有严格的构型，而是形成一种较为松散的构型.

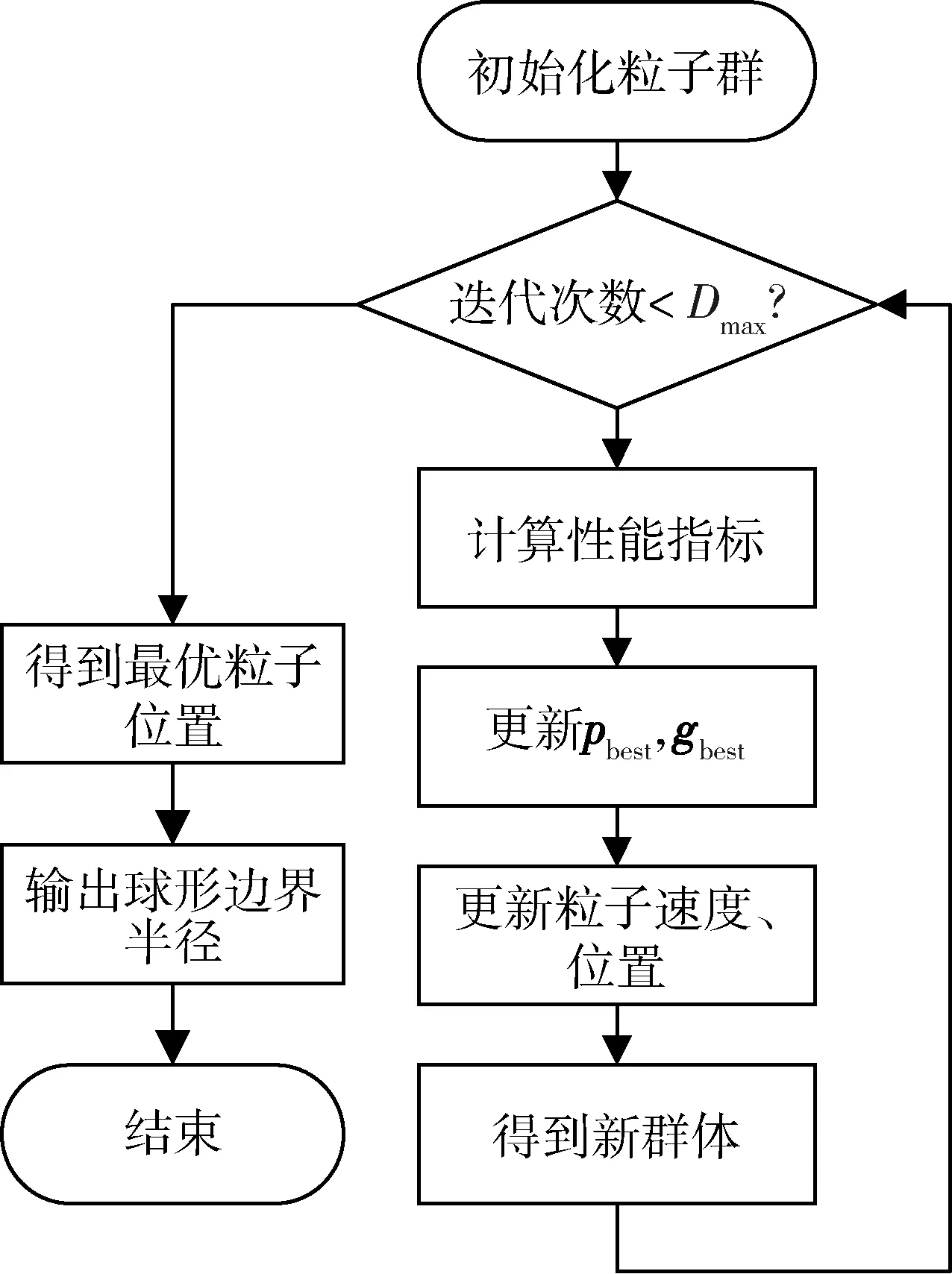
图6 粒子群算法寻找集群边界流程图Fig.6 Particle swarm optimization algorithm for finding cluster boundary

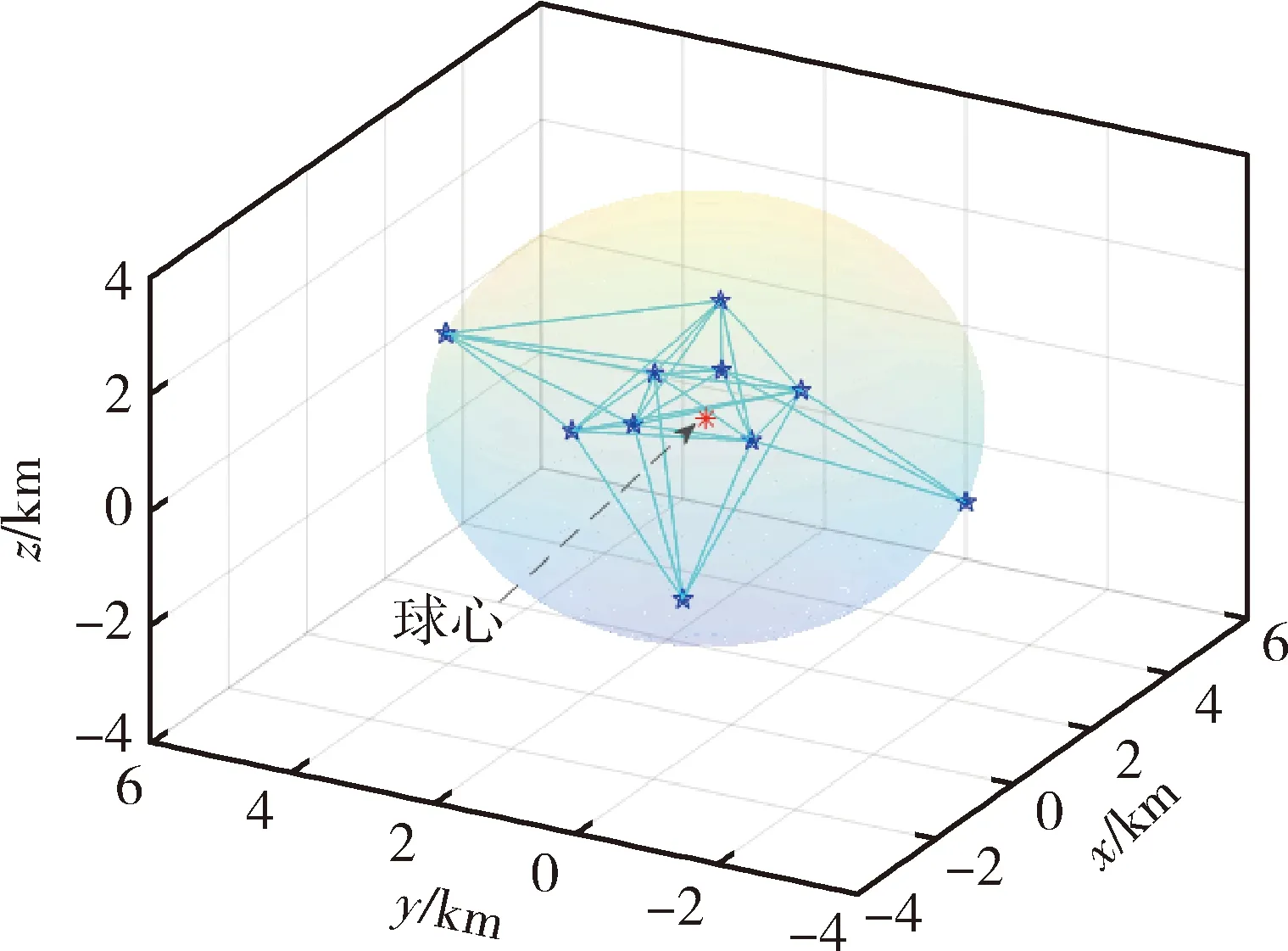
图7 集群球形边界及通讯拓扑Fig.7 Spherical boundary of spacecraft cluster and local communication topology

粒子群算法运行时间：0.075 265 s；全局最优粒子位置为：Xbest=(1.124,0.983,0.473)km；球形边界最小半径为3.458 km；

图8为粒子群算法搜索集群航天器最小球形边界的迭代过程，从图中可以看出，在第16代时，粒子群算法就已经收敛，球形边界半径为3.458 km，球心坐标为Xbest=(1.124,0.983,0.473)km.粒子群算法运行时间为0.075 265 s，即在0.075 265 s便可得到一次最小球形边界的反馈信息，该信息给控制器设计采样时间提供了参考.

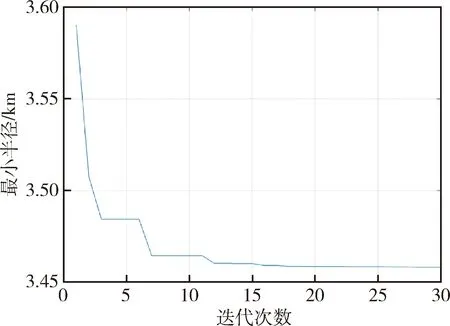
图8 最小半径搜索Fig.8 Search minimum radius

3 集群航天器边界控制

根据2.2中获得的集群航天器球形边界的球心位置以及半径作为反馈信息，3.1节中根据期望的集群边界设计出特定的球形空腔势函数来实现集群的边界控制，并在3.2中对集群航天器的边界控制进行了仿真，验证了算法的可行性.

3.1 球形空腔势函数的设计

集群边界进行控制指的是通过一定的控制算法，改变集群的边界尺寸(本文针中球形边界的半径).通过粒子群算法的迭代过程，可以找到集群航天器球形边界的中心以及半径.采用球形边界的航天器集群，在每一个采样时间内，集群的边界尺寸仅由最外层航天器所决定.因此在每个采样时间内，只需对最外层航天器(最外层航天器是在不断变化的)进行控制，使其保持在某一指定半径的球面上(或者球形空腔内)，由于蜂拥控制的作用，集群内部的航天器便会直接或间接地受到来自边界航天器地吸引力(或排除力)，从而具有向外扩张(或向内收缩)的趋势，因此，整个集群便完成了在球形空间内的分布.

设粒子群算法搜索到球边界的中心的坐标为(xc,yc,zc)，球半径Rc，期望集群球边界半径为R，空腔内径Rin=R-Δr,空腔外径Rout=R+Δr，Δr为小量.航天器i到球心的距离为Ri：

(10)

为了让控制只对最外层航天器起作用，引入bound向量，当航天器i到球心的距离Ri满足|Ri-R|≤ΔR时，bound(i)=1,表示航天器i是处于集群的边界(称之为边界航天器)，受到球形空腔势场力的作用；反之，bound(i)=0,表示航天器i是处于集群内部，不受到势场力的作用.

边界航天器i受到的斥力Fin、引力Fout表达式为：

(11)

其中Fmax为最大势场力.由式(11)可知，当航天器i到球心的距离Ri=R时，斥力和引力大小相同，方向相反，因此合力为零.

3.2 集群航天器球形边界控制仿真

采用粒子群算法对球形边界进行搜索时需要占用时间，频繁的搜索会导致计算速度变慢.在3.2节中，根据粒子群算法的运行时间，我们设置搜索过程的采样时间为1 s.为了方便观察集群航天器边界控制的效果，这里仅仿真8颗卫星.首先对集群施加蜂拥控制，观察集群相对位置稳定时的球形边界大小，以及集群中个体的分布情况.然后设置集群期望边界大小，同时加入边界控制，观察集群相对位置稳定时的球形边界大小，以及集群中个体的分布情况.

仿真参数设置如下：航天器数量为8；领航星反馈项lead=[1 0 1 0 1 0 1 0]；最大势场力Fmax=0.3；Δr=0.05 km；ΔR=0.1 km;期望球形边界半径R=3 km；只加入蜂拥控制时：

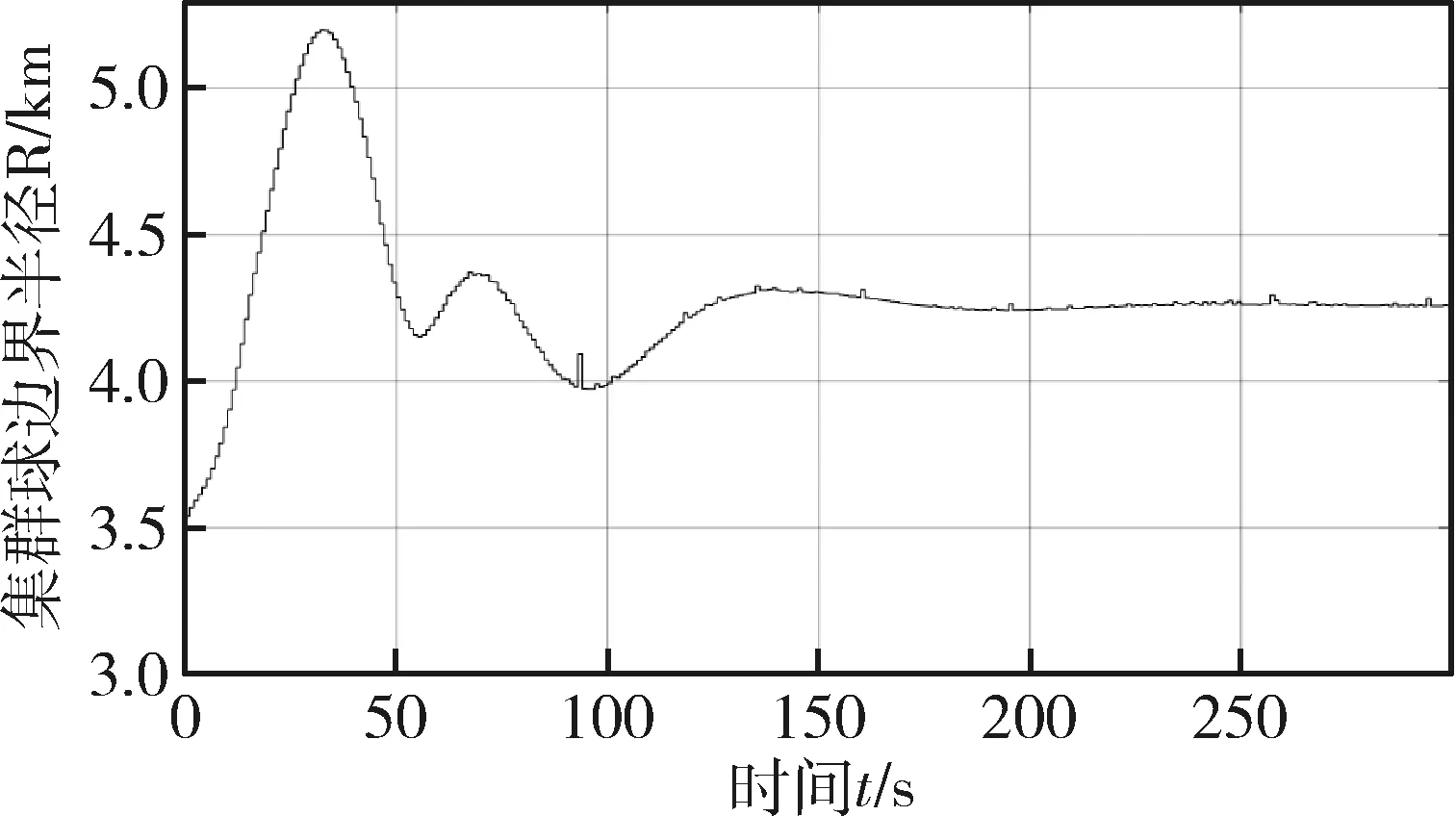
图9 集群边界变化(未加入边界控制)Fig.9 Changes in cluster boundary (boundary control not added)

图10 航天器到球心距离(未加入边界控制)Fig.10 Stance to center of sphere for every spacecraft (boundary control not added)

由图9知，只加入蜂拥控制时，集群航天器稳态时球边界半径为4.26 km.从图10看出各航天器在球形边界内的分布情况.航天器2、7、8位于距球心4.26 km的球形边界处，航天器4、5位于距球心3 km附近，航天器1、3、6位于距球心2 km附近.

加入蜂拥控制以及边界控制时：

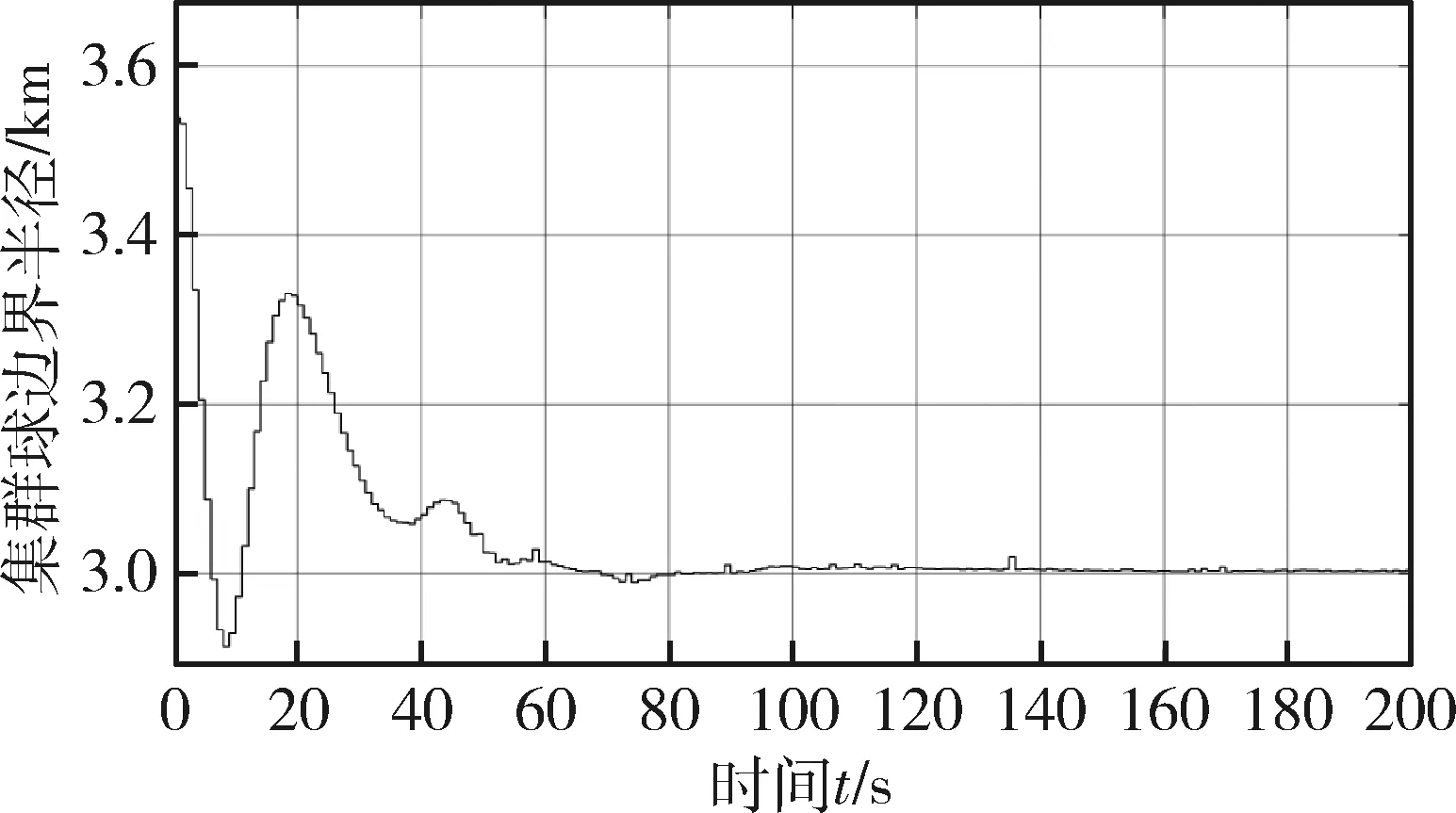
图11 边界变化(加入边界控制)Fig.11 Changes in cluster boundary (boundary control added)

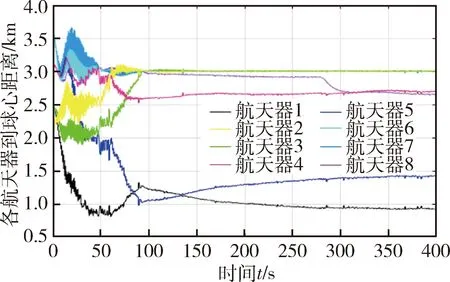
图12 天器到球心距离(加入边界控制)Fig.12 Distance to the center of sphere for every spacecraft (boundary control added)

加入边界控制后，集群边界与各航天器到球心距离变化分别如图11和12所示.从图11可看出，加入边界控制后，集群航天器稳态时边界半径为3.00 km，与期望边界3 km完全吻合.从图12中可以看出，航天器2、3、6、7位于距球心3 km的球形边界处，航天器4、8位于距球心2.7 km附近，航天器5位于距球心1.4 km附近，航天器1位于距球心0.9 km附近.对比文献[14]，基于球形空腔势函数的边界控制并没有使得集群全部分布在边界上，而是在整个球体内保持松散的分布，仅有个别航天器处于期望边界3 km处，这是由于边界控制只对边界航天器起作用，因此对集群内部影响较小，其影响仅仅在于使得集群有整体向内收缩的趋势.因此实现了集群航天器的边界控制.

4 结 论

本文提出了集群航天器在蜂拥控制下的边界问题，对集群航天器边界的研究意义与研究目的进行了分析.研究了球形边界参数的优化性能指标，并使用粒子群算法对实现了集群的最小边界搜索.并依据搜索结果设计了一种基于球形势函数的边界控制方法.仿真结果表明，加入边界控制后的集群能够保持在给定球形区域内.

集群在蜂拥控制下，稳态时可以保持固定构型，因此集群边界也固定.当面对一些特点任务需求时，如对障碍物环境中的避障，若对集群的边界进行控制，就不需要使集群中个体先分散后集中，避障问题因此变得十分简单.本文仅讨论了球形边界的控制算法，希望以后可以对盒形边界的控制算法进行研究，并考虑集群航天器姿控系统故障诊断与容错控制[15],同时针对具体的任务约束对集群航天器姿控算法进行重构[16].