机车变流柜散热器采用阻尼方式的数值模拟*

崔洪江, 张春利, 陈秉智

(大连交通大学 机车车辆工程学院， 辽宁大连 116028)

机车变流柜中的整流器将发电机组的交流电整流成直流电压，逆变器将蓄电池和直流电压逆变成交流电，以供给机车使用[1]。5 kW逆变单元散热器和9 kW整流单元散热器将工作部件热量吸收通过风道利用风机以强迫对流的方式把热量发散到机箱外，保证工作部件温度正常[2-4]。

WANG等[5]应用传热学理论对肋片散热器进行热阻计算、仿真和试验，并进行了对比研究证明。ZHANG等[6]建模仿真模拟发热块代替IGBT功率原件的方式对液冷板的流速、压力分布和温度分布等性能参数进行试验验证。ZHANG等[7]运用理论计算、数值模拟和试验研究对HXD1C电力机车辅助变流器进行散热设计。从WANG、ZHANG等文献中可得出热阻与流阻是散热器的两个重要参数，对散热器进行仿真计算时建立模拟发热块也是从热阻与流阻这两个角度进行出发建立的。但是试验得到5 kW逆变单元散热器热阻R=0.005 4(m2·K/W)和9 kW整流单元散热器热阻R=0.008 6(m2·K/W)，可见散热器热阻影响小可忽略不计。所以阻尼在不改变散热器耗热值和不考虑热阻的情况下，加载瞬态变化流阻曲线，在CFD计算时有利于误差的减小。

在Fluent软件建立变流柜模型时，用Ⅰ型和Ⅱ型阻尼替换机车变流柜关键部分5 kW逆变单元散热器和9 kW整流单元散热器，其中把阻尼耗热值为5 kW定义为Ⅰ型阻尼及耗热值为9 kW定义为Ⅱ型阻尼。由于实验得到两组Ⅰ型、Ⅱ型阻尼阻力曲线，所以通过给Ⅰ型和Ⅱ型阻尼进出口处设置监测点，得到Ⅰ型和Ⅱ型阻尼进出口处湍动流耗散率及熵产率，建立折线图应用流体力学及热力学第二定律进行对比分析，得到Ⅰ型阻尼和Ⅱ型阻尼合适的加载阻力曲线。

1 模 型

1.1 物理模型

图1是变流柜物理模型的左视图，由3部分组成：上部有4个百叶窗大小一样对称分布此为变流柜的进口，中间部分有4个5 kW逆变单元散热器和2个整流单元9 kW散热器呈对称分布，其中5 kW逆变单元散热器和9 kW整流单元散热器的具体结构如图2所示。下部为主风道与风机相连，此为变流柜的出口。

图1 变流柜的物理模型

1.2 计算模型

图3是变流柜计算模型的左视图，与物理模型的主要区别在于中间部分用Ⅰ型、Ⅱ型阻尼替换了5 kW逆变单元散热器和9 kW整流单元散热器。

图2 5 kW逆变单元散热器和9 kW整流单元散热器的具体结构

图3 变流柜的建模图

2 边界条件设定

该变流柜模型计算域的长×宽×高具体尺寸为2 700 mm×2 500 mm×3 000 mm，在出口处加载速度分别是35.16 m/s、39.07 m/s、42.98 m/s，其中对Ⅰ型阻尼和Ⅱ型阻尼所加载的阻力曲线如表1～表4所示。网格类型采用的是非结构化网格，生成网格数目是200万，计算采用κ-ε湍流两方程进行收敛计算。

表1 Ⅰ型阻尼加载第1组阻力曲线

表3 Ⅱ型阻尼加载第1组阻力曲线

表4 Ⅱ型阻尼加载第2组阻力曲线

3 流动性分析

3.1 理论分析

流体在阻尼内流动过程中，分别满足连续性方程、动量方程以及能量守恒方程。

连续性方程[8-10]如式(1)所示：

(1)

式中：ux，uy为流体速度在二维平面内x,y方向上的分量；

x，y为与流体速度相对应的坐标轴方向；

ρ为流体密度。

动量方程[8-10]如式(2)所示：

(2)

式中：u为流动速度；p为流动过程中的压力；S为流动过程中的广义源项；i，j为不同的流动方向。

流体湍动能[8-10]计算公式如式(3)所示：

(3)

式中：k为湍动能；ε为湍流耗散率；αk为流体Prandtl数；CK为速度梯度引起的湍动能项；Sk为流体湍动能源项。

流体的湍流耗散率[8-10]计算公式如式(4)所示：

(4)

3.2 性能分析

对阻尼流道内的流动情况进行数值模拟，流动过程遵循连续性方程、动量守恒方程以及能量守恒方程。为了更好地分析阻尼内部流体的流动情况提出如下假设：(1)流体连续介质的假定；(2)流体的黏性可以忽略，把流体看成是无黏性的理想流体；(3)流体的膨胀性可忽略不计。

该变流柜计算模型总共有4个Ⅰ型阻尼和2个Ⅱ型阻尼，并且在其进出口处设置12个监测点，监测点设置位置如图4所示,设置的目的是为了监测Ⅰ型和Ⅱ型阻尼在进出口处的速度、压力、湍动能和湍流耗散率。其中湍动能和湍流耗散率的数值越大越有助于阻尼散热，这是此次仿真在流动性能方面上选用湍动能和湍流耗散率来做评价指标的目的。根据边界条件设定的相关参数，应用Fluent软件得到Ⅰ型和Ⅱ型阻尼计算结果，如图5～图10所示，横轴表示监测点位置，纵轴表示阻尼的湍动能和湍流耗散率数值大小。

由图5、图6可见，(1)Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得湍动能在体积流量为4.62 m3/s监测点为2的位置处最大是9.6 m2/s2，在体积流量为3.78 m3/s监测点为1的位置处最小是2.65 m2/s2。(2)Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得湍动能在体积流量为4.62 m3/s监测点为2的位置处最大是9.97 m2/s2，在体积流量为3.78 m3/s监测点为1的位置处最小是3.12 m2/s2。(3)在外部条件相同的情况下，随着出口处加载的速度增大，在阻尼进出口处的湍动能数值也随着增大，原因是出口处加载的速度增大，在流经阻尼的气流中湍流的比例增多，进而导致了阻尼进出口处湍动能的数值增大。(4)监测点1、2、3和4湍动能数值差异最大，原因是包含监测点的阻尼距离下部主风道的距离是最近的，气体中湍流的比例最多导致的。

图4 散热器的监测点

图5 Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得湍动能的折线图

如图7所示，在体积流量是4.20 m3/s条件下，Ⅰ型和Ⅱ型阻尼加载第二组阻力曲线所得湍动能数值大于Ⅰ型和Ⅱ型阻尼加载第一组阻力曲线所得湍动能数值，说明对于阻尼在耗热值不变的情况下，随着相同流速下静压力的的增大，会导致湍动能数值也随着变小，这是符合实际情况的。因为散热器是通过系统中风机的风量来进行散热的，因此在流经散热器的风量会有一定的阻力，阻力不能太大，太大会减小风量通过散热器，从而达不到散热的要求。当然阻力也不能太小，太小会使风量流速加快不足以带走足够的热量，也达不到预想的散热的要求。由此可得Ⅰ型和Ⅱ型阻尼加载第二组阻力曲线是符合加载条件的。

图6 Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得湍动能的折线图

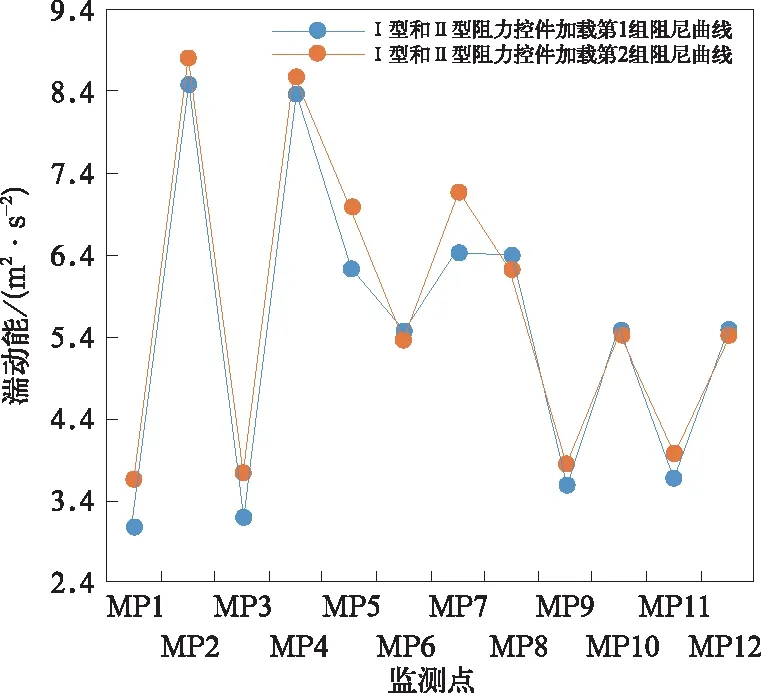
图7 在体积流量4.20 m3/s两组阻力曲线的湍动能的比较

由图8～图9可见，(1)Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得湍流耗散率在体积流量为4.62 m3/s，监测点7处的湍流耗散率的数值最大是887 m2/s2，在体积流量为3.78 m3/s，监测点1处的湍流耗散率的数值最小是116 m2/s2。(2)Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得湍流耗散率在体积流量为4.62 m3/s，监测点7处的湍流耗散率的数值最大是1 355 m2/s2，在体积流量为3.78 m3/s，监测点1处的湍流耗散率的数值最小是114 m2/s2。(3)在外部条件相同的情况下，随着体积流量的增大，阻尼进出口处的湍流耗散率的数值也不断的增大。(4)湍流耗散率的数值大小与湍动能的数值大小相比较，在湍动能数值大的阻尼，其湍流耗散率的数值小。

图8 Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得湍流耗散率的折线图

图9 Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得湍流耗散率的折线图

如图10所示，在体积流量是4.20 m3/s情况下，Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得湍流耗散率数值大于Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得湍流耗散率数值，其中在监测点5、7位置处，Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得湍流耗散率数值明显大于Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得湍流耗散率数值，由此可得Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线更有利于散热器的散热。

图10 在体积流量4.20 m3/s两组阻力曲线的湍流耗散率的比较

4 熵产分析

4.1 理论分析

热力学第二定律(熵增加原理)其表述为：不可能把从低温物体传到高温物体而不产生其他影响，或不可能从单一热源取热使之完全转换为有用的功而不产生其他影响，或不可逆热力过程中熵的微增量总是大于零。又称“熵增定律”，表明了自然过程中，一个孤立系统的总混乱度(即“熵”)不会减小。

在热力学中，熵是系统状态参数，它的物理表达式为：

或dS=dQ/T

式中：S表示熵，Q表示热量，T表示温度。

(1)进出口压降

ΔP=P1-P2

式中：P1，P2分别为监测进出口截面监测点的静压力，Pa；

ΔP为散热器的风阻，Pa。

(2)传热过程中的不可逆损失即熵产。考虑气流及阻尼构成的系统，在该系统中，气流为低温热源，熵变由下式计算：

式中：T1，T2分别为监测进出口截面监测点的温度，K;qm为空气质量流量，kg/s;cp为空气比定压热容，J/(kg·K);R为空气的气体常数，J/(kg·K);P1，P2分别为监测进出口截面监测点的静压力，Pa。

4.2 性能分析

熵产最小法：从热力学第一定律和第二定律的角度分析，自然界的一切实际过程都是不可逆的。散热器作为一种散热过程是典型的不可逆过程的装置，热量以导热、对流换热和辐射换热3种方式进行传递。散热器中的不可逆损失分为有限温差传热引起的不可逆损失和流体流动过程中克服摩擦阻力引起的不可逆损失，两者之和即是散热器中总的不可逆性损失。基于最小熵产原理，熵产越小，散热器不可逆损失越小，其综合性能越好[11-14]。

如图11、图12可见，(1)Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得熵产率在体积流量是4.62 m3/s，阻尼6的熵产率最大值是233 J/(kg·K)。在体积流量是3.78 m3/s，阻尼1的熵产率的最小值是11 J/(kg·K)。(2)Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得熵产率在体积流量是4.62 m3/s，阻尼6的熵产率最大值是91 J/(kg·K)，在体积流量是3.78 m3/s，阻尼2的熵产率的最小值是4 J/(kg·K)。(3)在Ⅰ型和Ⅱ型阻尼加载同一组阻力曲线，Ⅱ型阻尼熵产率明显大于Ⅰ型阻尼熵产率，原因是Ⅰ型阻尼耗热值低于Ⅱ型阻尼耗热值，其中有限温差传热引起的不可逆损失大于流体流动过程中克服摩擦阻力引起的不可逆损失，所以在熵产率中有限温差传热引起的不可逆损失占主导地位，导致了Ⅱ型阻尼熵产率大于Ⅰ型阻尼熵产率，当然也不可忽视流体流动过程中克服摩擦阻力引起的不可逆损失。

图11 Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得熵产率的折线图

如图13所示，在体积流量是4.20 m3/s条件下，Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得熵产率数值小于Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得熵产率数值，并且可见Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得熵产率数值是Ⅰ型和Ⅱ型阻尼加载第1组阻力曲线所得熵产率数值1/2倍，符合熵产最小法。所以从熵产最小法的角度出发，Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线更适合。

图12 Ⅰ型和Ⅱ型阻尼加载第2组阻力曲线所得熵产率的折线图

图13 在体积流量4.20 m3/s两组阻力曲线的熵产率的比较

5 结 论

采用阻尼的方式对机车变流柜中的散热器进行仿真计算，建立变流柜模型时中间部分用Ⅰ型和Ⅱ型阻尼替换了5 kW逆变单元散热器和9 kW整流单元散热器，应用流体力学及热力学第二定律，把湍动能、湍流耗散率和熵产率作为评价指标，得到Ⅰ型阻尼和Ⅱ型阻尼合适的加载阻力曲线。

(1) 在对散热器进行热分析时，由于阻尼在不改变散热器耗热值和不考虑热阻的情况下，加载的流阻曲线是瞬态变化，这样在CFD计算时有利于误差的减小，并且应用方便，可作为对散热器进行CFD计算的一种新的分析方法。

(2) 散热器在相同尺寸大小的情况下，第1组阻力曲线所对应散热器的翅片密度大于第2组阻力曲线所对应散热器的翅片密度，但是第1组阻力曲线湍动能、湍流耗散率数值均小于第2组阻力曲线湍动能、湍流耗散率数值，并且第1组阻力曲线熵产率大于第2组阻力曲线熵产率也不符合最小熵产率，说明散热器的翅片密度不能太大，否则适得其反。

(3) 把湍动能和湍流耗散率作为仿真结果处理的评价指标，而不是以往速度和压力，在3组不同体积流量加载的情况下，Ⅰ型和Ⅱ型阻尼加载第1、2组阻力曲线得到图3～图7计算结果，更加说明湍流的扰乱度大使得散热器翅片边界层厚度变小有利于其散热。

(4) 把熵产率作为仿真结果处理的评价指标，而不是温度，在3组不同体积流量加载的情况下，Ⅰ型和Ⅱ型阻尼加载第1、2组阻力曲线得到图11～图13计算结果，更加说明不可逆热力过程中熵的微增量总是大于零的。