基于起伏地层的曲面重力场快速高精度正演

郑翾宇， 柳建新， 陈 波， 赵广东， 陈龙伟， 郭荣文

(1.中南大学 地球科学与信息物理学院，长沙 410083;2.有色资源与地质灾害探查湖南省重点实验室，长沙 410083)

0 引言

地形模型的正演是重力数据定量解释的基础。正演问题中的地形改正和等效补偿，反演问题中所涉及的重要密度界面(如沉积层底部界面、地壳与地幔的分界面等)，都需要一个快速而准确的算法来计算出地形模型产生的重力场。地形模型重力场的正演方法可分为空间域和频率域两类[1]。空间域方法是将地形模型剖分成多个便于计算的规则单元体，分别计算每个单元体在观测点处产生的重力异常，最后累加求和得到该地形模型总的重力异常。这些规则单元体产生的重力场具有解析表达，通过解析式可以精确地计算出空间任意一点处的重力异常场。许多学者在空间域正演方法方面做了大量工作，Hubbert[2]用线积分的形式来计算任意二度体的重力场，同时也采用了图形法来计算重力场；Nagy[3]给出了长方体模型的重力场解析式，同时指出复杂形体可以用长方体作为基本单元叠加来模拟，为重力场的地形校正提供了基本的思路；Paul[4]给出了以三角形为面元的任意三度体的重力场；Plouff[5]将Talwani[6]的薄板公式推广到边界为任意多边形的直立棱柱体的异常解析式，同时利用该解析式做地形校正；Li[7]回顾和整理了直立长方体、上下底面为任意多边形的直立棱柱体以及任意多面体模型的重力场及其高阶导数在全三维空间的正演公式，并初步研究了重力场及磁场在场源边界处的连续性问题；Nagy[8]详细讨论了直立长方体模型的重力位及其三阶以下导数在全空间的连续性问题，详细推导了各奇点处的解析积分式，并分析了奇点处的极限性质；Garcia-Abd eslem[9]推导了密度随深度呈三次多项式变化的直立长方体的重力场解析公式，并用之前的解析和数值相结合的方法[10]对结果进行了验证。这些研究极大地丰富和完善了空间域重力正演方法，但是空间域方法的解析式往往较为复杂，推导过程比较繁琐，尤其当场源体模型较为复杂，观测点数较多时，由于计算次数会随着模型剖分个数以及观测点数急剧地增加，计算过程将会特别耗时，计算效率成为制约空间域方法运用的瓶颈。

相比于空间域方法，频率域方法引入了快速傅里叶变换(FFT)，计算速度得到显著提升。同时，在异常频谱的表达式中，场源体的几何特征表现为简单的乘积因子，异常频谱的表达式更为简洁和紧凑，频率域方法也因其具有的独特优势而被广泛采用。相鹏等[11]采用频率域方法研究了磁性界面；冯娟等[12]用频率域方法研究了三维密度界面和重力位场之间的关系；姜永涛等[13]采用了频率域算法研究了中国西部地区的莫霍面深度；卢鹏羽等[14]基于重力全张量数据采用频率域算法研究了密度界面。

频率域算法的发展从20世纪60年代开始，Bhattacharyya[15]给出了长方体磁化的磁场频率域表达式，并指出在频谱表达式中场源形体和物性等参数是彼此分离的乘积因子，从而场源体的物性及尺寸、埋深等各参数可以直接利用异常场的频谱来分析；Schouten[16-17]采用FFT算法计算了层状体的磁场异常。基于这一思路，Parker[18]将快速傅里叶变换引入重力位场正演，提出了用于地形校正的Parker公式，该方法是从频率域计算均一密度的长方体叠加地形模型的位场。在利用传统的Parker公式正演起伏地层产生的重力异常时，往往存在一定的误差。一是傅里叶变换时产生的；其次Parker公式本身存在一定的缺陷，这一缺陷影响正演结果的收敛速度，导致正演误差的产生。Forsberg[19]在详细研究了长方体叠加的场源体模型的重力场之后，将Parker公式中级数展开的思想改进为空间域级数展开法，再利用FFT算法计算一系列褶积的和；冯锐[20]将Parker公式的密度由原来的横向变化推广至沿深度方向按指数或线性变化的情况；Xia等[21]提出了通过增加上下界面平均值来提高Parker公式的数值稳定性加速级数收敛的思想；Chai[22]详细介绍了偏移抽样方法，该方法大幅提高了频率域重力正演精度；柴玉璞[23]提出了变衰减系数指数和变系数多项式密度模型的Parker公式，为了提高傅里叶算法的数值精度文中采用乘子法[24]和偏移抽样方法；柴玉璞[25]将偏移抽样方法进行了重新的疏导和整理并发展为一套完整的理论，将离散傅里叶变换的精度提高数十倍，减小了基于傅里叶变换的频率域位场正演误差；Wu等[26]指出，采用标准FFT方法正演产生不同程度畸变的原因是离散傅里叶变换这种算法(梯形积分)不能很好地逼近傅里叶这一震荡积分，从这个角度出发引入偏移参数并提出Gauss-FFT算法，该算法不仅大幅减小了频率域计算时“边界效应”、“混叠效应”、“诡源效应”等问题，同时还极大地提高了频率域方法的计算精度。这些频率域方法的提出以及傅里叶算法的改进，为频率域方法提供了广阔的应用空间。

笔者从重力位场出发对Parker公式进行了重新的推导，参考Xia等[21]的思路，引入上下界面平均值，将界面的绝对起伏值转化为相对平均界面的起伏量，加快了正演的收敛速度，提高了正演公式的数值稳定性。考虑到实际情况下的观测面并非水平，甚至有时我们需要一个曲面上的重力异常值，对此提出了一个曲面观测算法，将传统的水平观测面拓展到了起伏观测面，实现了上下界面起伏地层在起伏观测面上的快速高精度重力正演计算，并采用Gauss-FFT算法进一步保障正演的数值精度。

1 方法原理

1.1 正演理论方法

自Parker将傅里叶变换引入到重力场正演计算并推导出著名的Parker公式以来，这种以快速高效著称的频率域算法已被广泛应用于地形校正和其他正演计算，但是传统的Parker公式存在一定的缺陷，当界面起伏较大时不能保证正演结果的数值稳定。我们对Parker公式进行了重新的推导，并引入上下界面平均值，改进后的Parker公式具有更高的数值稳定性。

如图1所示的直角坐标系中，x-y平面置于水平，z轴竖直向上，与重力方向一致。重力异常的场源体是由上下起伏面h1(ξ,η)和h2(ξ,η)所围成的地层模型，场源体的坐标为(ξ,η,ζ)。观测面为z=z0的平面， 观测点坐标为(x,y,z0)。

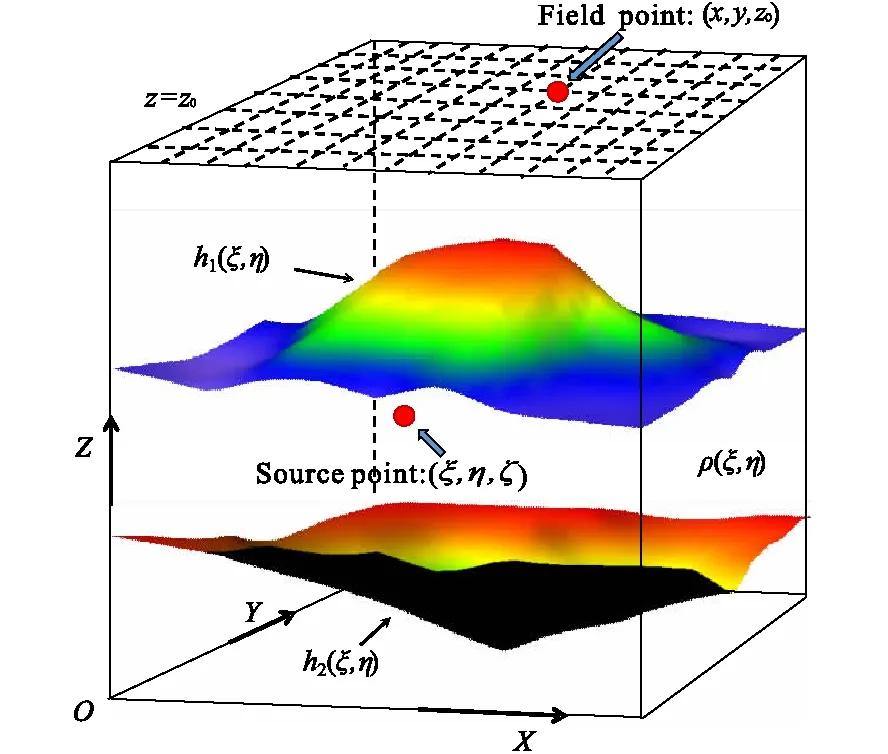
图1 起伏地层模型和观测面示意图Fig.1 Complicated undulating stratigraphic model and observational schematic diagram

场源体在观测面上某一点处产生的重力位U(x,y,z0)(简记为U)可表示为式(1)[27]。

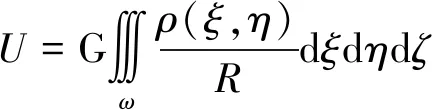
(1)

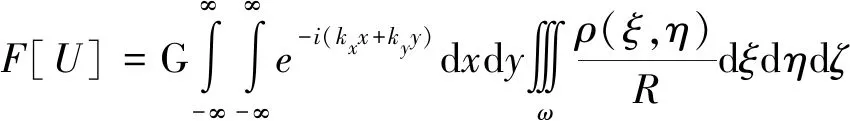
(2)

式(2)中：Kx、Ky分别表示x、y方向上的波数。将式(2)改变积分顺序，根据傅里叶平移性质(3)和Bracewell[28]推导的变换式(4),我们可以将式(2)经变换得到式(5)。

f(x-ξ)↔F(k)e-ikξ

(3)

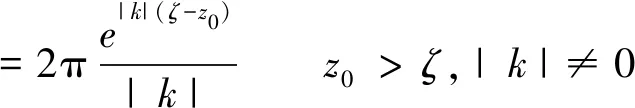
(4)

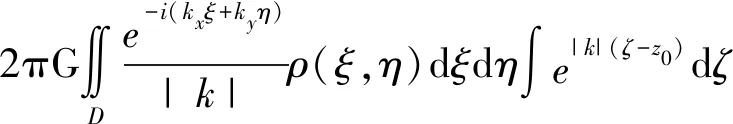
(5)

将地层的上、下面h1(ξ,η)和h2(ξ,η)代入式(5)并对ζ求积分可得式(6)。

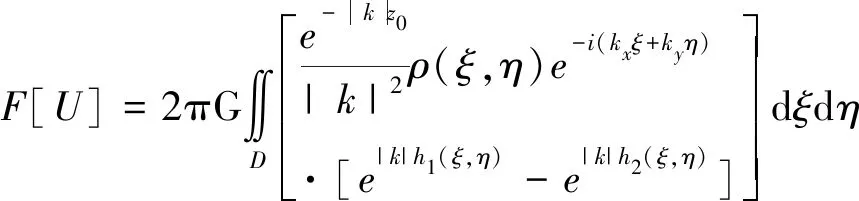
(6)

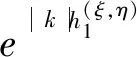
对重力位求z向偏导，得到上下界面起伏地层模型在水平观测面上产生的重力异常的频率域表达式为式(7)。

F[Δg]=-2πG

(7)

式(7)即为快速收敛的起伏地层正演公式，与传统的Parker公式(8)相比具有更高的数值稳定性。

(8)

采用传统的傅里叶变换计算时，正演结果会出现不同程度的畸变。为了避免这一问题，均采用4节点的二维Gauss-FFT算法[22]。

1.2 曲面观测

在前人的研究工作中，正演选取的观测面均为水平观测面。受到地形等外界条件的影响，实际情况下的观测面并非水平面，如野外重力数据采集时，观测面是随地形变化的起伏面。因此，快速且精确地正演出场源体在起伏观测面上的重力异常，是一项具有实际意义的研究工作。

如图2 (a)所示，场源体是上、下起伏面h1(ξ,η)和h2(ξ,η)之间的地层，观测面为z=z(x,y)的起伏面。为了计算起伏观测面上的重力异常，采用泰勒级数展开法，依据泰勒级数展开理论，起伏面上的重力场可以用式(9)展开。

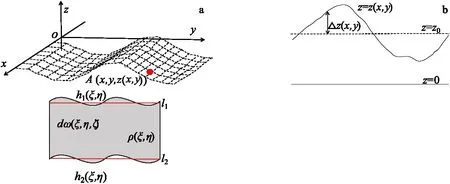
图2 示意图Fig.2 Sketch map(a)曲面观测示意图；(b)泰勒级数展开法示意图

g(x,y,z(x,y))=g(x,y,z0)+

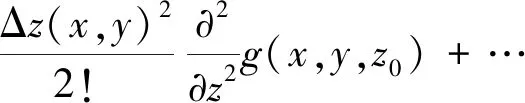
(9)

其中：g(x,y,z0)表示平面z=z0上的位场；Δz(x,y)=z(x,y)-z0(图2(b))。

由式(9)可知，利用泰勒级数法的基本思想，可以根据平面z=z0上的重力位场g(x,y,z0)及其对应的各阶导数值，来逼近曲面z=z(x,y)上的重力位场值g(x,y,z(x,y))。依据傅里叶变换的性质，各阶导数可以按照式(10)转换到频域计算[23]。

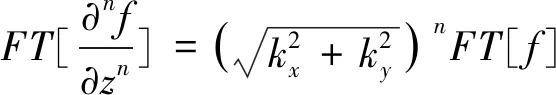
式中:FT[]表示傅里叶变换；IFT[]表示傅里叶反变换。

根据起伏地层在水平观测面上产生的重力异常正演式，可以直接求出起伏面z=z(x,y)对应的泰勒展开面z=z0上的重力异常f(x,y,z0)。根据泰勒展开式(9)和傅里叶变换中导数的转换性质(10)，可得到起伏观测面z=z(x,y)上的重力异常为式(10)。

(10)

起伏观测面上重力异常的精度受泰勒展开面z0的取值和泰勒级数展开项数的影响，一般来说z0取起伏面的平均值最佳，泰勒级数展开项数越多正演结果越精确，但计算量也随之增加。

2 模型算例

建立简单的模型体，从模型实验数据出发检验正演算法的可靠性。由于空间域算法是将场源体剖分成单个的直立棱柱体，而每个棱柱体在观测点上产生的重力异常可以通过解析式准确计算，因此我们将空间域正演结果作为标准来衡量正演算法的精度。

2.1 起伏地层的正演计算

如图3(a)所示，在z轴竖直向上的坐标系中，产生重力异常的场源体上下界面为凹凸起伏面，顶、底界面的平均值分别为l1=-1 km,l2=-3 km；模型在x方向和y方向均为256 km,即0≤ξ≤ 256 km,0≤η≤ 256 km；场源体模型的密度为ρ=800 kg/m3；观测面为z=1.5 km的水平面，x方向和y方向上的观测点数Nx=Ny=256，网格间距dx=dy=1 km。

首先采用Nagy[3]提出的空间域方法，计算出场源体在观测面上产生的重力异常，如图3(b)所示。空间域正演结果的平均值为-61.80 mGal，标准差为8.09 mGal。总体来说，重力异常数值在中间较大往四周逐渐减小，在边界处取得最小值-19.89 mGal。

采用Parker[14]提出的上下界面起伏地层的正演公式和改进的正演公式(7)分别对图3(a)所示的起伏地层做正演计算(图4)。

图4(a)所示的正演结果和空间域结果相比大体一致但在数值上略有偏差，图4(b) 直观的给出了采用传统Parker公式正演的误差大小和分布规律，由图4(a) 、图4(b)可知：传统Parker公式的正演误差主要集中分布在起伏地层的边缘处，对于地层没有起伏变化的区域，正演误差相对较小。总体而言，绝对误差数值范围从-18 mGal至26 mGal，最大相对误差约为10%。

图4(c)为改进的Parker公式正演结果，平均重力异常为-61.81 mGal，标准差为8.08 mGal。图4(c)的正演结果在数值上与空间域方法的正演结果几乎一致，数值的变化和分布规律几乎相同。

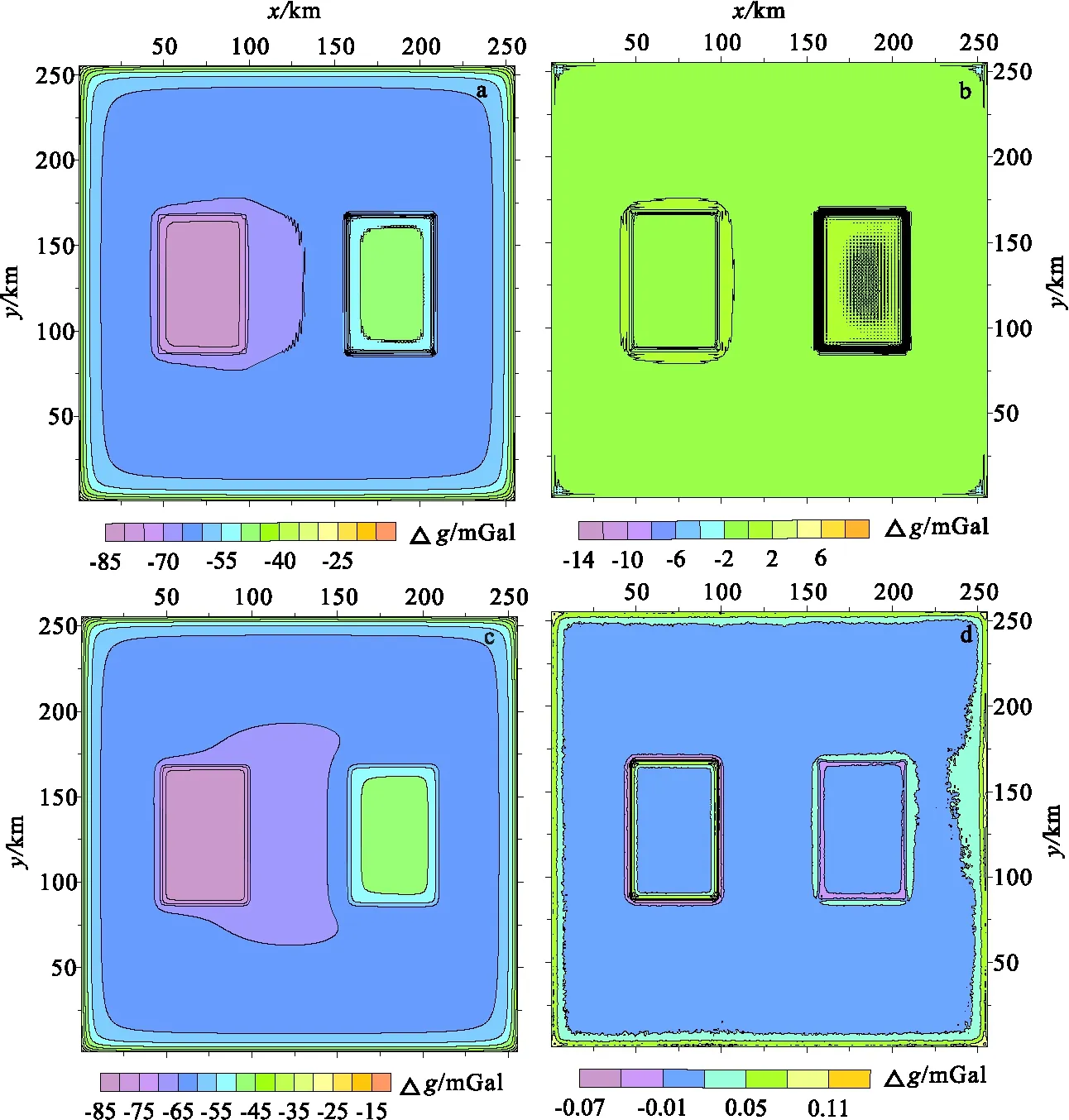
图4 正演结果和误差Fig.4 Forward results and error maps(a)传统Parker公式正演结果；(b)传统Parker公式正演误差；(c)改进的Parker公式正演结果；(d)改进的Parker公式正演误差

由图4(d)可知，改进后的Parker公式最大相对误差约为0.1%。

该模型算例表明，改进后的Parker公式(7)在起伏地层的正演计算中具有更高的数值精度，而正演数值精度提高的关键点在于增加上、下界面平均值这两个参数后，将界面的绝对深度转化为相对界面平均值的起伏量，加速了正演结果地收敛。

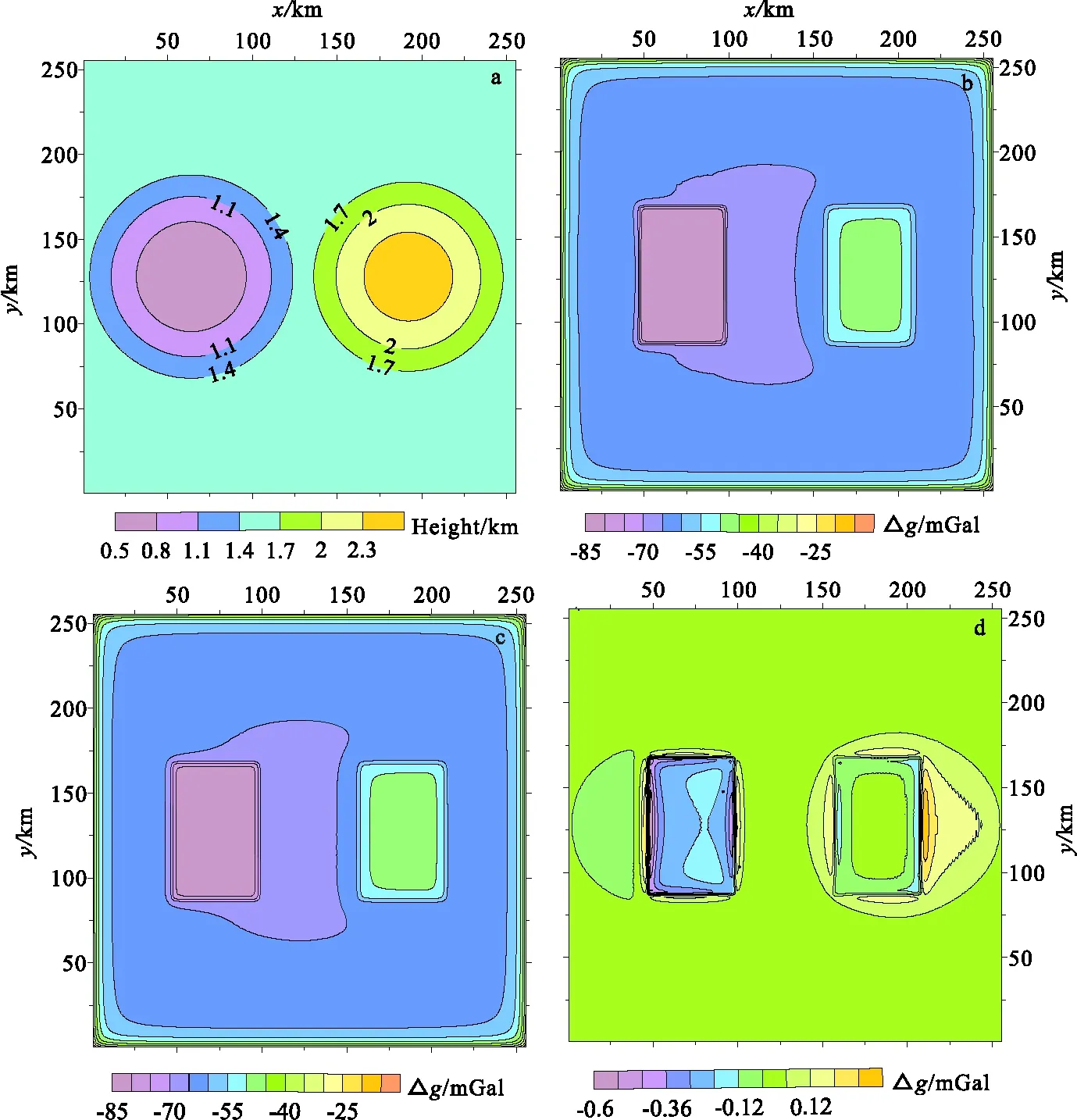
图5 起伏观测面和正演结果Fig.5 Undulating observation surface and forward results(a)观测面示意图；(b)空间域方法正演结果；(c)本文提出的频率域方法正演结果；(d)新频率域方法正演误差

2.2 起伏地层的曲面观测

场源体模型与上面一致,不同之处在于观测面由原来z=1.5 km的水平面变为如图5(a)所示的起伏面，观测点数和网格间距保持不变，x方向和y方向上的观测点数Nx=Ny=256，网格间距dx=dy=1 km。观测面是相对z=1.5 km水平面存在正弦函数形凸起和凹陷的起伏面，凸起区域是以(64,128)为中心64 km为半径的圆形区域，凹陷区域则是以(192,128)为中心64 km为半径的圆形区域。

图5(b)是空间域方法正演得到的起伏观测面上的重力异常。重力异常的平均值为-61.86 mGal,最大和最小的重力异常值分别为-83.34 mGal和-19.89 mGal,标准差为8.27 mGal。

图5(c)是曲面正演理论，从频率域正演得到的起伏观测面上的重力异常，泰勒级数的展开面为z=1.5 km的水平面，展开项数为10项。总体来看，由图5(c)可知，其正演结果与空间域方法计算结果5(b)几乎一致，在数值方面，平均重力异常为-61.85 mGal，最大和最小的重力异常值分别为-82.83 mGal和-19.96 mGal,标准差为8.24 mGal。

图5(d)为频率域方法的正演误差。从误差图可知，频率域正演具有较高的数值精度，平均相对误差小于百分之一。

空间域方法的正演时间为2 165 s，频率域方法的正演时间仅需16 s。测试计算机配置为CPU-Intel(R) Core(TM) i5-4590，主频为3.30 GHz，内存为8 GB。由此可见该方法在保障正演精度的同时也兼具很高的计算效率。

通过大量的模拟实验发现，曲面观测的正演计算受泰勒级数展开平面和级数展开项数的影响。当泰勒展开平面取起伏面的平均值时正演精度最高，离平均值越远精度越低。泰勒展开项数则会影响正演精度和效率，正演精度随着泰勒展开项数的增加而提高，计算效率则相反。为了取得较高的正演精度，同时保留频率域算法的效率优势，泰勒级数的展开项数一般取6项到10项。

图6 带地形的密度界面起伏模型Fig.6 Density interface with undulating terrain model

2.3 起伏地形的密度界面模型正演模拟

上述模型算例均是计算起伏地层在某一观测面上产生的重力异常，而Parker公式除了用于地形校正以外，也常用于密度界面的研究。图6为带地形的密度界面起伏模型，观测面为地表起伏面z=z(x,y)，数值与图5(a)一致。密度界面为ζ=h1(ξ,η)，在(98,128)和(158,128)两点处分别存在一个以30 km为半径，幅值为3 km的正弦形凸起和凹陷。密度界面的平均值h0=-5 km,密度差ρ2-ρ1=400 kg/m3。

图7 正演结果图Fig.7 Forward results(a)空间域正演结果；(b)频率域正演结果

计算起伏密度界面在水平观测面上产生的重力异常时，公式 (7) 被简化为式(12)。

F[(h1(ξ,η)-h0)n·ρ(ξ,η)]

(12)

根据式(12)计算出起伏密度界面在z=1.5 km平面上产生的重力异常，计算出地表观测面z=z(x,y)上的重力异常，正演结果如图7所示。

图7(a) 为空间域方法正演结果，图7(b)为频率域方法正演结果，两个正演结果的等值线图几乎一致。为了进一步研究频率域方法的正演精度和计算效率，将两种方法的正演结果进行了统计分析，整理的结果如表1所示。

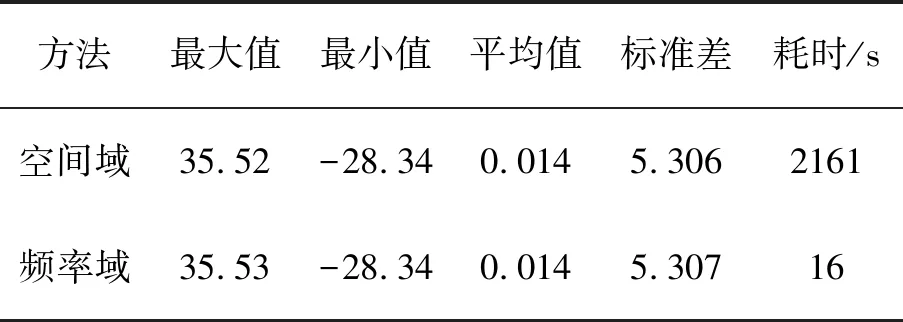
表1 空间域方法和频率域曲面观测方法正演对比Tab.1 Forward comparison of spatial and requency domain methods

从表1可知，本文提出的曲面观测面算法在正演图6所示的起伏密度界面模型时，具有非常高的数值精度，在计算效率方面相对于空间域正演方法更是提高了一百多倍。

3 结论

首先对起伏地层的重力正演方法做了简单的综述，总结了空间域和频率域两种方法各自的优点与不足，并对方法的发展情况作了简单的介绍。随后针对频率域Parker公式存在的问题展开讨论，从重力位场出发对Parker公式进行了详细的推导，并加入上、下界面平均值两个参数对传统的正演公式加以改进。在此基础上，提出了一种曲面观测算法，实现了起伏地层起伏观测面的快速高精度重力正演计算和带地形密度界面起伏模型的快速高精度正演。从模型实验可知：

1)改进后的Parker公式在起伏地层的正演计算中具有更高的数值精度，其核心在于将界面的绝对深度值化为相对起伏值，大幅减小了由于数值不稳定而产生的正演误差。改进后的Parker公式可用于地形校正，沉积层校正以及密度界面的正反演等方面的研究。

2)本文提出的曲面观测的正演方法，在保证正演精度的同时计算效率相对传统空间域方法高出两个数量级，是一种计算起伏观测面上重力异常场的有效方法。