复杂条件二维重力场及重力张量场空间波数域正演方法

李颖梅， 戴世坤， 李 昆， 陈轻蕊， 凌嘉宣

(中南大学 地球科学与信息物理学院，长沙 410083)

0 引言

重力场及重力张量场的数值模拟在地球物理勘探中有着重要作用，但是复杂二度体的重力数值模拟不易实现，因此研究高效、高精度的复杂形体重力场及重力张量场数值模拟具有重要意义。目前关于二度体重力场及重力张量场的正演计算方法主要可划分为解析方法与数值方法两大类。

1)解析式法。解析式法是利用数学计算方法计算不同模型的解析解，主要是对规则二度体和密度呈现不同函数特征分布的重力场与重力张量场解析解的求解。Kwok[1]用共轭复数法推导了截面为任意多边形、密度随水平和深度呈线性变化的二度半体的源内外重力异常；Atienza[2]采用解析与数值相结合的方法推导了密度随水平和垂直方向二次变化的二度体重力异常解析表达式；安玉林等[3-5]介绍了具有连续物性分布和任意边界的二维和三维重磁场正反演方法，并推导了截面为规则形状的二度体及其组合体复重磁场表达式；贾真[6]对Won和Bevis提出的新算法的数值不稳定性作了适当修正；王彦国[7]推导了二度体背斜及三度体球冠两种模型的重力公式；孙明国[8]推导了截面近似圆形和截面为任意形状的二度体矿脉重力表达式，并给出了重力水平一阶导数、垂向一阶导数和垂向二阶导数的解析公式；苏和明等[9]重新推导了倾斜台阶重力异常公式，消除了原表达式间断点的现象；求解析解时，存在奇异点计算和数值不稳定所造成的误差问题，而且当异常体模型形状不规则、密度分布很复杂时，解析解的求解相当困难。

2)数值方法。数值方法主要包括微分法和积分法。微分法利用泊松方程和边界条件求解整个区域节点场值的线性方程组，微分法的关键在于边界条件的加载。朱自强等[10]在二维重力张量的正演计算中引入有限元法；Reeder等[11]提出一种二度体重力异常计算的有限元方法，采用滑动窗口法来减少边界效应，使用卷积算子来提高计算效率。积分法的优势在于只需对异常体进行剖分，自动满足边界条件。主要分为两大类，一类是通过多个具有解析表达式的规则二度体逼近，以拟合复杂地质构造，或利用求积分的数值算法求解。例如：Ku[12]提出采用高斯数值积分法和三次样条法计算二度体重力异常；徐世浙等[13]提出一种利用高斯数值积分计算三维变密度体重力异常的正演方法；张岭[14]利用三角棱柱体组合的重力异常逼近截面为任意形状的非均匀密度二度体重力场；另一类是谱方法，这种方法结合傅里叶变换等数值算法的优点，将卷积问题变为乘积问题，大大提高了计算效率。吴乐园[15]提出一种用于重磁位场正演的频率域高精度正演的Gauss-FFT新方法，Gauss-FFT法避免了零波数的计算，在同等计算精度的要求下，计算速度比标准FFT扩边法要快得多。

针对复杂截面形状、任意密度分布二度体重力场和重力张量场正演问题，笔者从积分方程出发，给出一种新的组合矩形模型波数域重力场和重力张量场表达式，并借助Gauss-FFT方法和三次样条插值方法，克服了传统FFT截断边界效应问题，实现了起伏地形上重力场与重力张量场高效、高精度的二维正演，为实现快速反演与人机交互解释提供借鉴。

1 正演方法

为模拟任意截面形状、任意密度分布的复杂二度体，采用矩形剖分(图1)。将研究区域剖分成Nx×Nz个小矩形，(ξi,ζj)表示小矩形中心坐标。每个剖分矩形内密度为常值，剖分矩形个数越多，模型刻画越精细，越逼近实际的复杂二度体。上述剖分方式简单、灵活，适用于复杂二度体反演和人机交互解释建模。依据重力异常的叠加原理，复杂二度体可以转化为矩形二度体组合模型下重力场及重力张量场的正演问题。

图1 复杂二度体正演示意图Fig.1 Sketch of forward modeling for complex two-dimensional gravity anomaly

研究重点在于快速、准确计算矩形二度体组合模型产生的重力场。在图1给出的剖分方式下，重力场计算“精确”表达式为式(1)～式(2)。

gz(x,z)=

(1)

gx(x,z)=

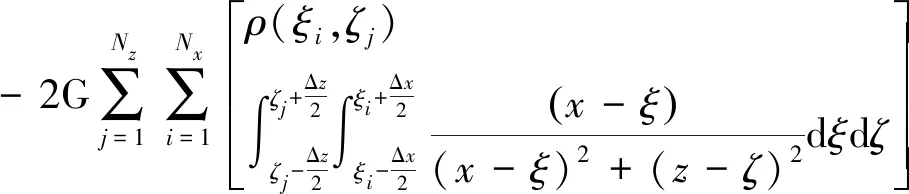
(2)

重力张量表达式为式(3)～式(4)。

gzx(x,z)=

(3)

gxx(x,z)=

(4)

式中：G为万有引力常数；Nx、Nz分别表示研究区域x,z方向剖分矩形的个数；Δx、Δz表示矩形x、z方向采样间隔，每个矩形水平方向采样间隔Δx相同；可以根据密度垂向变化决定Δz大小，这样可以进行灵活采样，有助于减小计算量。矩形二度体的中心坐标记为(ξi,ζj)，密度为常值，记为ρ(ξi,ζj)。

本文提出的波数域重力高效、高精度二维正演方法，重要环节之一是对式(1)～式(4)两边施加一维傅里叶变换，可以推导得到新的组合模型正演波数域表达式为式(5)～式(8)。

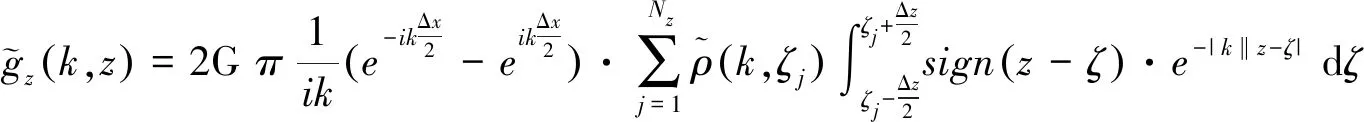
(5)

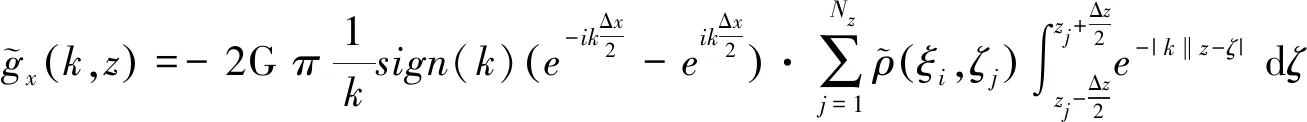
(6)

(7)

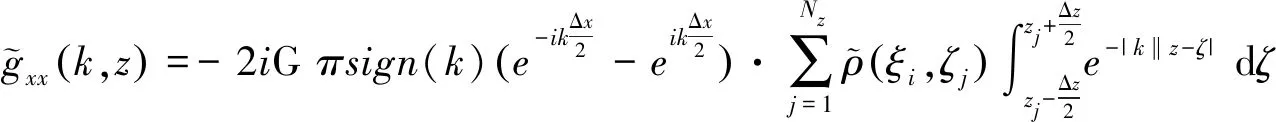
(8)

式中：k表示x方向的波数，

(9)

式(9)在形式上类似于一维离散傅里叶变换，在数值计算实现时，可利用快速傅里叶算法(FFT)实现[16]。

式(5)中，sign(z-ζ)和sign(k)分别表示z和k的符号函数，表达式如下：

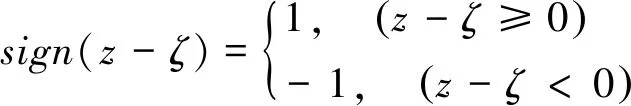
(10)

(11)

式(5)～式(8)为求解的四个空间-波数混合域重力场与重力张量场的解析表达式，进行一维傅里叶反变换，可得空间域重力场及重力张量场。以重力异常gz为例，反傅里叶变换的表达式为式(12)。

(12)

式(5)～式(8)和式(12)是计算二度体重力场与重力张量场的理论基础。

在实现一维傅里叶反变换数值时，采用Gauss-FFT方法，既保证计算效率，又克服传统FFT算法存在的截断效应及零波数奇异问题，可提高傅里叶反变换数值计算精度。

上述新算法能够实现起伏地形上场的快速计算，笔者采用的策略是：根据地形的分布，确定最高点和最低点之间等间距分布的多个不同高度水平网格上的场值；再采用三次样条插值，获得起伏地形上的场值。这种方法的优势在于可利用插值获得地势复杂难以观测的区域内的场值。

方法流程如下：

1)给定剖分区域矩形单元个数以及观测平面参数，起伏地形包含在剖分区域内。

2)根据地质体密度分布给每个矩形的剩余密度进行赋值。

3)根据式(1)～式(4)，利用一维傅里叶变换计算获得空间-波数混合域重力场/张量式(5)～式(8)。

4)对空间-波数混合域重力场/张量反傅里叶变换得到空间域下重力场/张量。

5)采用三次样条插值，获得起伏地形上的场值。

2 模型算例

为了验证本文提出的二维正演快速算法的计算精度，以及对复杂条件的适应性，设计矩形模型，分别计算了水平线和起伏地形上的场值。将数值解与解析解进行对比，验证算法的正确性和高效性。算例中取x轴为东西方向，y轴为北南方向，z轴垂直向下。测试计算机配置为CPU-Intel(R) Core(TM) i7-4770，主频为3.4 GHz，内存为16 GB。傅里叶反变换采用4个高斯点的Gauss-FFT方法实现。

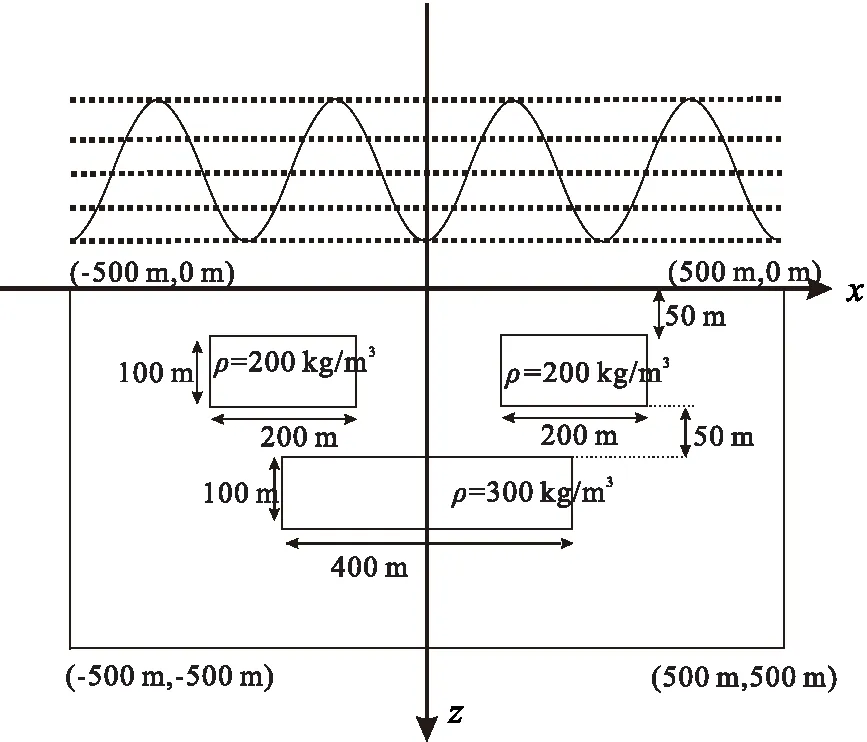
图2 算例模型和起伏观测线示意图Fig.2 Synthetic model and fluctuation of the observation lines

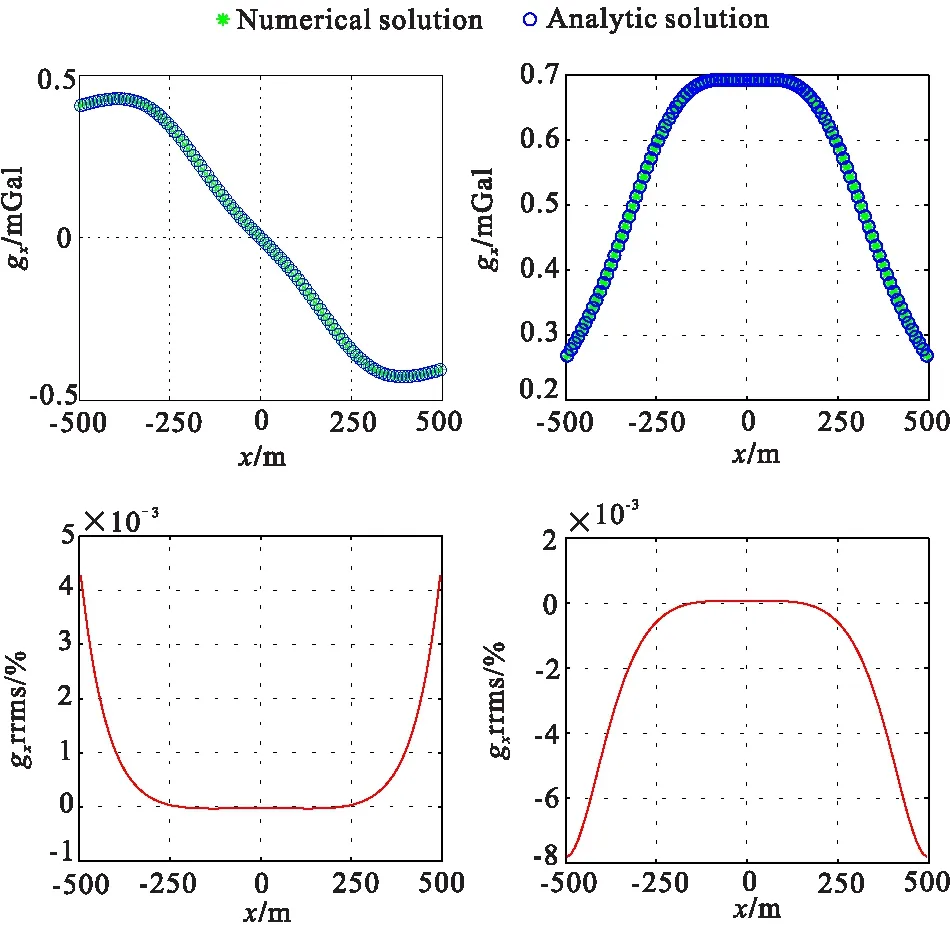
图3 水平测线重力场数值解与解析解的曲线图及相对均方根误差Fig.3 The numerical solution and the analytical solution of gravity fields when profile is horizontal as well as the relative error between the two

图4 水平测线重力张量数值解与解析解的曲线图及相对均方根误差Fig.4 The numerical solution and the analytical solution of gradient tensors when profile is horizontal as well as the relative error between the two

模型算例的计算区域如图2所示，矩形的x方向和z方向均匀剖分，整个区域剖分的网格个数100×100，围岩密度0 kg/m3。利用本文算法计算水平线上z=-100 m上的重力场与重力张量场的值，并与解析解进行对比。图3所示为水平线上重力场gx,gz数值解与解析解的数值对比及相对误差；图4所示为水平线上重力张量场gxx,gzx数值解与解析解的数值对比及相对误差；从图3与图4可以看出，重力场与重力张量场的数值解与解析解具有较高吻合度，相对误差均较小，由于截断效应，重力场在边界处相对误差稍大，最大约为0.004%；在边界处与零值附近，重力张量数值计算误差稍大，最大约为0.4%。由图3和图4可知，张量的变化趋势较场更加剧烈，场的计算精度高于张量。

为了研究起伏地形上场值的计算精度随着插值曲线条数的变化，设计一个正弦函数变化的起伏地形，在观测区域的函数表达式为式(13)。

(13)

起伏地形上最高点与最低点的z方向坐标为-300 m和-100 m。

引入相对均方根误差，统计整条起伏观测线上场值的误差。该误差统计方式能突出大异常值所占的比重，计算公式为式(14)。

(14)

其中：rrms表示相对均方根误差；N表示x方向的节点数；gi表示重力异常(重力张量)数值解；Ti表示重力异常(重力张量)的解析解。

图5为起伏地形上重力场及重力张量场相对均方根误差随水平插值个数的变化趋势图。从图5中可以看出，起伏地形上重力场与重力张量场的计算精度随着插值个数的增加而提高。当用3个不同高度进行插值时，起伏地形上重力场的rrms已小于0.5%，而重力张量场rrms较大，最大约为2.5%。当选取的高度网格节点个数大于11时，起伏地形上重力场与重力张量场的rrms几乎不再变化，计算精度达到最优。图6所示插值个数11时，起伏地形上重力场与张量的曲线图。从图6中可以看出，起伏地形上数值解与解析解的吻合度很高；选取15个不同高度网格节点上的场值进行插值时，算法耗时仅为0.020 s，这说明本文提出的插值策略是可行的，同时也证实了算法在二度体重力场及重力张量场正演计算时，具有很高的计算精度和计算效率。

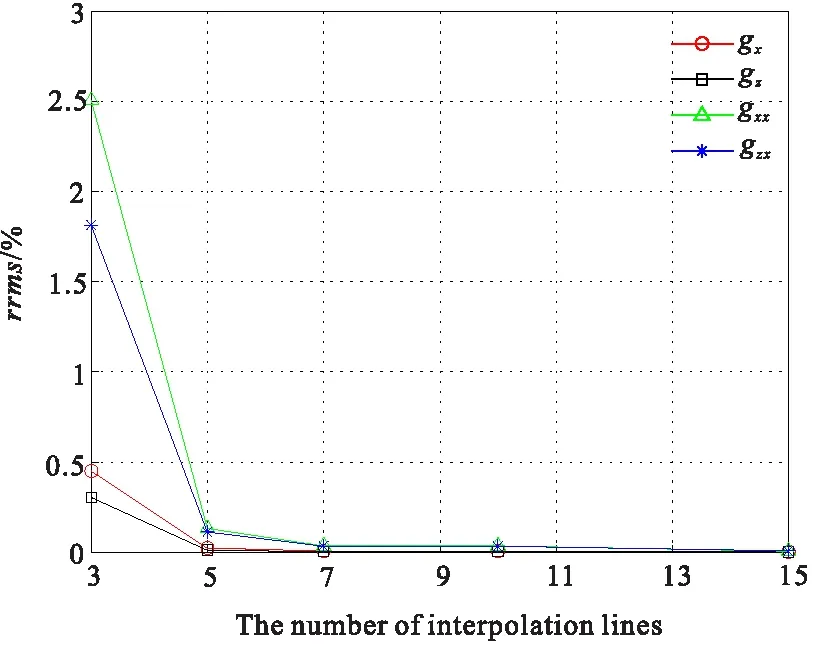
图5 相对均方根误差随插值个数变化Fig.5 Rrms with a varying number of interpolation dots

图6 起伏观测网格节点重力场与重力张量的数值解与解析解Fig.6 The numerical solution and the analytical solution of gravitational fields when profile is horizontal as well as the relative error between the two

利用文献[17]中格尔木—花海子剖面岩石圈二维密度结构模型，拟合密度分布的模型如图7所示，计算地面z=0 m水平线上重力场和重力梯度如图8所示。

图7 格尔木-花海子剖面岩石圈二维密度结构模型Fig.7 2-D lithospheric density structure along the profile from Golmud to Huahaizi

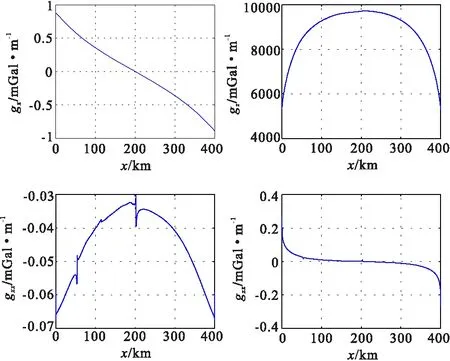
图8 水平测线重力场与重力张量数值解Fig.8 The numerical solution of gravity fields and gradient tensors when profile is horizontal

3 结论

笔者针对任意密度分布情况下、起伏观测线二度体重力场及重力张量高效、高精度正演问题，提出了一种基于Gauss-FFT和三次样条插值的空间波数混合域正演算法。结论如下：

1)算法采用矩形二度体组合模型的波数域计算公式，将二维空间域卷积拆分成波数域多个一维积分累加，大大减少了计算量。同时，不同波数场的计算相互独立，采用并行算法可进一步提高计算速度。

2)每个波数对应的空间域一维积分可得到解析解，计算精准；利用Gauss-FFT反傅里叶变换，避免零波数计算，能克服传统FFT法的截断效应，进一步提高了计算精度。采用矩形二度体组合，能模拟地下任意复杂地质条件，从而实现重力勘探复杂条件二度体高效、高精度正演计算。

3)网格剖分100×100时，水平网格节点重力场相对误差最大仅为0.004%，重力张量场为0.4%；计算起伏地形15个不同高度水平网格上的场值时仅用0.02 s；网格数1 000×1 000时，计算时间1.3 s。可见，随着网格数量的增大，算法耗时近似线性增长，算法具有良好的伸缩性。

4)笔者提出的算法，还可应用于三维重磁问题的求解，为重磁数据的高效、高精度反演、人机交互正反演解释提供了新途径。