中国教育回报率的长期变动(1991-2016)——基于收入差异的分位数回归研究

韩文龙 刘 璐

(西南财经大学 经济学院，四川 成都 611130)

一、问题的提出

教育问题不仅仅关系着创新生产力的发展，也关乎社会的和谐稳定。放眼未来，到2035年中国要基本实现社会主义现代化，中等收入群体比例明显提高，城乡区域发展差距和居民生活水平差距显著缩小，到本世纪中叶实现全体人民共同富裕的宏伟目标，则教育应当发挥社会公平的稳定器作用。教育是提高国民素质、提高创新能力和发展生产力的基础工程，教育对经济发展有两方面作用，一是直接对个人收入的提高，二是间接改善社会经济环境，如教育有助于减少失业和犯罪[1]。其中教育对个人收入的提高又被称为教育的回报率，这一指标是激励个体接受更高教育、产生更多社会正外部性的关键因素。研究中国教育回报率尤其是不同教育阶段的回报率变动趋势，对于经济社会发展具有重要意义。

由于没有长时段的微观调查数据，中国近几十年来的教育回报率没有形成一致的长期估算。考虑到教育成本数据难以获取，本文采用明瑟收入函数法，使用CHNS①、CLDS②和CGSS③合并后的1991～2016年的数据，分别对均质的年教育回报率、地区和城乡教育回报率以及异质的不同教育阶段回报率的变动趋势和影响因素进行了分析。在研究方法上，本文在最小二乘法的基础上，运用了不会损失样本量的分位数回归方法[2]，这一方法不仅使回归结果更为稳健，还可以将传统的个人教育回报率细分为高收入群体、中等收入群体和低收入群体的教育回报率，从而实现了对中国教育回报率影响因素和变动趋势的结构性分析。

二、文献综述

(一)国外教育回报率估计研究

关于教育回报率估计的研究最早兴起于国外。共有四大估计方法：(1)20世纪50年代后期的“详细阐述法”，将回报率定义为在某一时刻上收益流等于成本流的折现率[3]。使用该方法需要事先获得年龄收入曲线，经常表现为对样本数据的锯齿状敏感且本身难以获取。为了克服这一困难，发展出平滑处理的方式，将相等教育水平的从业人员按年龄分组回归，然后再利用该回归结果建立年龄收入曲线。改良后的这种方法对数据量要求很大，且教育投资的内部回报率对外设参数(教育对收入增加的影响程度)非常敏感。(2)20世纪70年代由经济学家雅各布·明瑟(Jacob Mincer)提出的明瑟收入函数方程，将教育作为一个重要变量，教育变量的系数就是个人收益率[4]。该函数中没有涵盖教育的个人成本，但是作为一个工资定价模型，它揭示了工作经验、教育年限等因素对工资报酬的影响，从而决定人力资本最佳教育投资水平。尽管这种方法不是数学意义上的收益率，但凭借其特有的劳动力市场经济含义和简单易行的方法，成为研究教育回报率使用最广泛的方法，为此，本文也拟运用这种方法。(3)“捷径法”，该方法将个人收入用特定教育水平的劳动者的平均收入来代替，在个人收入数据难以获取时有一定意义。(4)加里·贝克尔(Gary S Becker)提出的成本收益法，也被称为净现值法[5]。这里教育总成本既包括机会成本也包括直接成本，净收益是教育潜在收益和教育总成本之差，该方法因难以计算且数据难以获取而很少被用到。

国外学者也注意到不同教育阶段对个人教育回报率有着异质性的影响。乔治·萨卡罗普洛斯(George Psacharopoulos)运用不同国家数据得出,教育的社会回报率随着教育阶段的提高而减少,个人教育回报率除了发达国家外高等教育回报率不低于中等教育回报率[6]。值得注意的是，这一结论是教育回报率在部分国家的变化情况,并不意味着所有国家的教育回报率随着教育阶段变化的特点都是如此。有学者对尼日利亚的数据进行分析研究发现，不管是被雇佣人员还是自我创业人员,教育回报率都随着教育水平的提高而增加[7]。中国的教育回报率如何随教育水平提高而变化以及是否呈现先低后高的规律值得我们进一步探究。

(二)中国教育回报率变动趋势研究现状

关于中国教育回报率的研究，早期学者更加关注中国教育回报率的测算及其变动趋势，尤其是考察九年义务教育普及和大学生扩招政策对教育回报率变动趋势的影响[8-10]。随着中国教育回报率研究逐步向着模型精细化方向发展，学者们更加关注实证分析中的计量偏误及处理方式[11-12]，对于基础的教育回报率变动趋势研究成果相对较少，但是近年来出现的大学生就业难现象和教育无用论的甚嚣尘上，中国教育回报率是否不再呈现过去的上升趋势而出现新的下降趋势、这种趋势在不同的教育阶段是否存在差异成为亟待解决的理论问题。

有关中国教育回报率的实证研究，最早影响力较大的是李实等估算出的1988年中国教育回报率为3.8%[13]，该数据样本来自于中国社会科学院经济研究所收入分配与改革课题组。此后赖德胜又利用该课题组在1995年的大规模调查，得到中国教育回报率为5.73%，教育回报率在1988～1995年总体呈现出增长趋势[14]。后该课题组样本数据发展成为CHIP数据④，李春玲利用该数据库得到2002年中国教育回报率进一步提高到11.4%的结论[15]。有关20世纪末中国教育回报率的研究，也有学者使用国家统计局城镇入户调查数据，得到教育回报率由1988年的4%上涨到2001年的10.2%[16]。进入21世纪，随着国内微观调查数据的发展，对中国教育回报率的实证研究有了进一步的深入，所使用的模型也不仅限于普通最小二乘法(Ordinary Least Squares,简称OLS)，而是越来越多地使用多层线性模型、工具变量等方法对原有模型进行修正。如范静波利用CGSS数据，基于OLS研究发现，教育回报率2003年为9.9%,2005年增长到15.5%，2006年又下降到14.3%，2008年小幅上升为14.6%。值得注意的是，使用同样的数据，范静波基于扩展后的OLS，得出的教育回报率远低于基于OLS所得数据[17]。这也就是说，即使是同一个数据库，使用不同时期的数据，得到的教育回报率是不具有比较基础的；同样的数据使用不同计算方法得到的结果，也不能作为教育回报率变动趋势的依据。因此，在一个较长的时间维度上，用统一的方法来测算教育回报率及其变动趋势就显得尤为重要。CHNS从1989～2011年共进行了十次调查抽样，众多学者利用CHNS数据对中国教育回报率进行了分析。邓峰等利用层次分析法发现，从全国范围来看，教育收益率从1989～1993年间处于缓慢上升的趋势，1993～2004年间上升势头更加快速，2004～2006年间处于平稳状态，2006～2009年间则出现了回落现象[18]。钟甫宁等也利用CHNS数据，基于工具变量模型发现，教育回报率在1988年为2.7%，到2003年增长为6.3%[19]。从以上研究中可以发现，1988～2004年教育回报率呈总体上升趋势已成为学界共识。对于这一期间教育回报率增长的原因，可以归纳为以下三个：①工资决定机制改革对教育回报率的直接激励作用；②多种所有制结构改革的影响; ③改革开放后劳动力市场化逐步施行[20-22]。

现有的教育回报率估计模型，大多是以受教育年限作为解释变量使用明瑟收入函数模型进行估计，这样做有一个隐含的假设条件，即教育年限和个人收入被假设为是线性相关关系，个体所受的教育对收入的影响是相同的。但是，现实中不同等级的教育回报率是异质的，比如高等教育阶段的回报率远高于义务教育阶段。在劳动力市场中，用人单位也往往根据个人所接受的最高学历教育而不是总体受教育时间来确定工资水平。学界也将其称为羊皮纸效应或文凭效应，认为教育具有文凭筛选功能，高等级教育文凭获得者比低等级教育文凭获得者有更高的薪酬[23]。国内对于各个教育阶段的回报率都有研究，但更多的是关注于某个特定的教育阶段。虽然也有部分学者对不同教育阶段的回报率进行了分析，如娄世艳估算出2005年平均教育回报率为6.18%，小学教育回报率为6.67%，初中教育回报率为4.47%，高中教育回报率为3.86%，大专教育回报率为11.25%，本科教育回报率为13.75%，研究生教育回报率为5.37%[24]，但是对不同教育阶段教育回报率在长时间内的变动趋势进行对比分析的研究成果较少。

(三)简要述评

虽然对前期教育回报率的实证研究及其变动原因的研究文献较多，但是限于微观数据库数据的时间跨度较小，有些研究的时间甚至还是10年前，没有体现出最新的教育回报率变动趋势。因此，对于近年来的教育回报率变动趋势还需要新的数据进行验证，同时，为了使各个年份的结果有比较基础，选取较长时间跨度的数据，用相同的方法来分析是十分必要的。基于此，本文考虑到单个微观数据库难以达到较长时间的跨度，因而对多个数据库进行了合并处理，使用CHNS、CLDS和CGSS合并后的1991～2016年的数据，分别对均质的年教育回报率、异质的不同教育阶段回报率、地区和城乡教育回报率的变动趋势和影响因素进行了分析，以期对我国教育回报率近年来的变动趋势作出一些边际贡献。

三、研究方法和模型

(一)教育年限回报率模型

1974年明瑟提出了著名的明瑟收入函数。该收入函数模型采用线性形式简单有效地解释了个人教育对个人收入的影响，在研究教育回报率时被广泛使用。其基本的表达式如下：

ln(Income)=a+b×edu+c1×

(1)

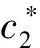
基本的明瑟收入函数考虑的因素较少，在原有模型中加入其他控制变量，构成扩展的明瑟收入函数。扩展的模型为如下形式：

ln(Income)=a+b×edu+c1×

(2)

参考现有文献，本文选取的控制变量Xj主要有性别、城乡虚拟变量和地区类别变量。为了避免虚拟变量陷阱，选取女性、农村作为基准类别变量，不计入模型的解释变量中。此时，dj表示的是非基准的虚拟变量相对于基准虚拟变量来讲的收入差别，符号为正表示比基准类别收入多，符号为负则说明收入比基准类别少。对于教育回报率这一核心主题来讲，加入Xj控制了可能造成偏误的其他因素，改变了拟合方程的截距项。

(二)不同教育阶段回报率模型

为了更符合实际地刻画各个教育阶段的教育回报率，解决非线性问题，本文在传统年教育回报率的分析基础上，将原有解释变量教育年限edu替换为最高学历diploma这一类别变量。反映各教育阶段教育回报率的模型如下：

ln(Income)=a+b×diploma+c1×exp+

(3)

变化后，系数b含义与之前不同，变为最高受教育阶段相比较于基准教育阶段而言，在其他条件不变的情况下收入将增加b×100%。基准教育水平取决于diploma这一类别变量，后文将未受过教育作为基准变量，系数b则体现了获得某阶段教育者相比较于没有接受正规教育者收入增加的百分比，尽管形式上仍是线性模型，但却用类别变量的方式一定程度上解决了异质性问题。其余系数解释与传统明瑟教育回报率一致。

(三)收入差异的分位数回归方法

回归分析是在自变量信息确定的情况下，探求因变量的变动规律，模型对现实的解释力越强越好，在样本中表现为模型误差的最小化。由于正负误差会抵消，常用误差取平方后再加总求和最小化(即OLS),或者误差取绝对值后加总求和最小化(即最小绝对偏差估计量法，Least Absolute Deviation Estimator,简称LAD)，分位数回归属于LAD方法范畴。

假设条件分布y|X的q分位数yq(Xi)是X的线性函数，如下所示：

yq(Xi)=Xiβq

(4)

其中，βq就是分位数回归偏系数向量,q是分位数，βq会随着q的变化而不同。q估计量可由(5)式求得：

(5)

根据式(4)和式(5)得yq，为ln(Income)q工资收入的对数，Xi代表一系列自变量的向量。q的数值表示在回归平面上的数据占全体数据的百分比，如当q=0.9，则1-q=0.1，表示模型得到的是90%的条件分位数，90%的数据分布在回归平面上，还有10%分布在回归平面以下。OLS与分位数回归的系数解释意义有所不同，如在本文中的系数b，OLS估计式是教育年限或不同教育阶段这一自变量对工资收入的平均边际影响,分位数回归估计式是教育年限或不同教育阶段这一自变量对工资收入q分位数的边际效果。OLS只能提供一个平均数，分位数回归却能提供很多不同分位数的回归结果。如果条件分布的形状随着解释变量而变化，不同分位数回归的系数也将不同，这有利于处理数据异质性问题。此外，分位数回归所求的是最小误差绝对值，相比较于误差平方和OLS而言，对于异常值的敏感度很低，因而更具有稳健性。

本文使用分位数回归方法，将传统的个人教育回报率细分为高收入群体、中等收入群体和低收入群体来研究，正是对应着分位数回归中因变量q的不同数值。值得注意的是，此时因变量是调查时期个体的收入，高中低收入群体代表的也是个体接受访问(终点)时期的收入群体情况，而非个体初始时期的群体情况。

教育对社会群体的流动性的影响可以从两个时点出发来衡量，一是站在个体的初始点，此时不同群体的个体通过教育可以改变收入从而实现社会阶层的流动(例如当高收入群体教育回报率低于低收入群体时，最终的结果既可能是最初高收入群体在个体终点时变为低收入群体；也可能是高收入群体仍为高收入，但相较低收入群体两者的差距在缩小或扩大)；二是站在个体的终点，此时高收入群体的教育回报率低于低收入群体，隐含着如果没有教育，那么终点处的高收入群体与低收入群体的差距将进一步拉大。从这两个时点出发，都能说明教育对社会群体流动性的影响，第一种更符合一般的思维方式，但第二种方式在搜集数据和处理时更为简洁，两者最终都能较好地衡量教育对社会群体流动性的影响。本文采取的是第二种衡量方式。

四、数据说明

(一)数据来源与样本分布状况

本文使用了三个微观调查数据库共12年的混合截面数据，分别是CHNS、CGSS和CLDS。由于微观调查数据库录入的是个体的数据，如能够统一口径，可以使不同的数据库相互补充，最大化利用各方资源。关于人力资本方面的微观数据库合并文章虽然鲜见，但仍不乏成功先例，如李磊等[25]利用CHIP、CHNS、CGSS和CULS⑤最终形成了2000～2009年的混合截面数据来研究金融发展对企业家精神的影响。本文合并的数据库中，使用年份最多的数据库是CHNS，该调查分别于1989、1991、1993、1997、2000、2002、2004、2006、2009、2011年进行了十次抽样调查。CGSS使用了2013年的数据，CLDS使用了2012、2014、2016年的数据。在这三个数据库中，个体的人口统计特征、就业状况、工作收入以及教育状况等数据信息都是可以获取的。

在本文的模型中，还包括年龄、城乡、性别、省份、受教育年限等变量。CGSS2013、CLDS2012、CLDS2014和CLDS2016都没有直接的年龄变量，但是有出生年月信息，本文用调查时期的年份减去出生年份从而得出每个个体的年龄。CGSS2013、CLDS2012和CLDS2014没有个体受教育年限这一变量，仅提供了个体接受过的最高教育水平。CHNS1989-1991年的数据既提供了教育年限变量，也提供了最高的受教育水平变量。但是CLDS、CGSS和CHNS调查数据中接受过的最高教育水平这一类别变量并不统一，本文以CHNS为标准，将CGSS2013中的受教育程度的13个等级和CLDS2012、CLDS2014和CLDS2016中的11个等级按照最相近原则划归为标准的7个等级，然后再通过受教育程度的最高等级生成个体的受教育年限，具体赋值方法如下：未曾受过教育为0年，小学毕业为6年，初中毕业为9年，技术学校毕业为11年，普通高中、中专毕业为12年，大学专科毕业为15年，大学本科毕业为16年，研究生毕业为19年。在城乡控制变量中，CHNS数据库中分为城市和农村这一虚拟变量，而CGSS2013的户籍类型划分较为细致，包括农业户口、非农业户口、蓝印户口、居民户口、军籍和没有户口七类，本文将农业户口之外的全部归为城镇人口，从而使城乡控制变量一致。上面三个数据库共涉及29个省(自治区、直辖市)，本文在此基础上生成了东部、中部、西部三个地区变量，划分标准以国家统计局的划分标准为主，值得注意的是，东北地区的辽宁被划为东部地区，吉林和黑龙江被划分为中部地区。本文对合并后的样本进行了如下筛选：①为了真实反映收入与教育的关系，剔除了未满18岁和超过65岁的个体，这是因为这部分人群存在严重的生命周期偏误，未满18岁的个体大多还在接受教育，而65岁的人群大多数已经退休，个人收入会比年轻时期有较大幅度的下降；②根据受访者对于工作情况的回答对样本进行了筛选，剔除了未回答的、目前没有工作的个体样本；③剔除了其他变量没有观察值的个体样本。

最终，本文一共得到92 125个观察值，样本的分布状况如表1所示。

表1 样本分布状况(样本总量92 125个)

注：12个年份比例之和为1，东部、中部、西部三地区比例之和为1，地区类别变量东部、中部和西部由省(直辖市)类别变量产生：东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东10省(直辖市)；中部地区包括黑龙江、吉林、山西、安徽、江西、河南、湖北、湖南8省；西部地区包括内蒙古、广西、重庆、四川、贵州、云南、陕西、甘肃、青海、宁夏和新疆11省(自治区、直辖市)。

由表1个体样本的分布状况可知，样本的城乡、性别比例大致相当，涉及东部、中部和西部共29个省(自治区、直辖市)，时间跨度从1991～2016年长达26年(CHNS数据中1989年的数据只有周工资，而没有本文研究的年工资、奖金和其他来自工作的收入这一指标，因而本文选取的数据是从1991年开始)，数据的分布特征能够较好地代表中国整体的教育回报率状况。

(二)变量选取与描述性统计

在被解释变量选择上，CHNS数据对个人和家庭收入进行了详细的调查，在个人收入方面有按件计价的工资、每月工资、农林牧副渔等各项收入。在综合考虑本文的研究内容与CGSS2013、CLDS2012、CLDS2014、CLDS2016共有的收入指标，采用年工资、奖金和其他来自工作的收入总和指标作为因变量。与单纯采取月工资收入或者是小时工资相比，所选指标能够一定程度上探测出隐性收入，从而更为准确地衡量教育对个人收入的影响。在研究中国教育回报率的变动趋势过程中，为避免价格效应对回归结果造成偏误影响，本文把1991年作为基准年对被解释变量进行CPI指数平减。解释变量使用了两种数据，一是个体回答的最高学历的类别变量，二是通过个体回答的受教育年限或最高学历推测出的个体受教育年限。其他变量方面需要注意的是：工作经验这一变量并不是调查问卷直接获得的，而是用受访者的年龄减去教育时间再减去6，使用这一方法来描述工作年限已被普遍使用[26-27]。由于工作经验对收入的影响往往是非线性的，在明瑟收入函数模型中也会将工作经验的二次项加进来。本文中所使用到的变量统计性描述如表2所示。

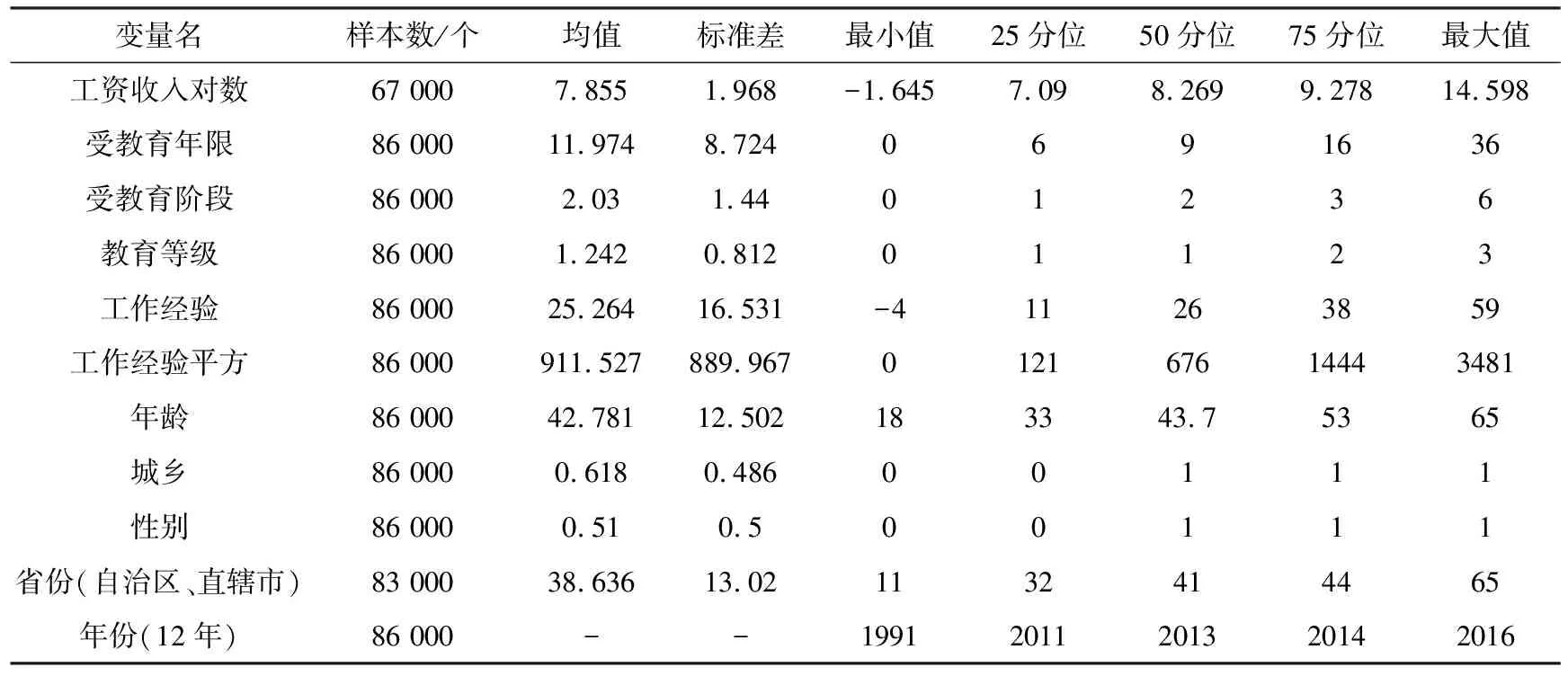
表2 变量的统计性描述

五、实证分析

本部分在模型设定的基础上，同时使用OLS和分位数回归来分析均质的年教育回报率和异质的最高等级教育回报率，着重关注教育回报率的影响因素和变动趋势，然后通过分组回归进一步探究地区差异、城乡差异在教育回报率及其变动趋势上的不同。主要从两个方面分析：一是不考虑教育异质性的教育年回报率，二是考虑教育异质性的不同教育阶段的教育回报率。

(一)教育年回报率分析

1.教育年回报率变动趋势

教育年回报率是以受教育年限作为解释变量，不考虑不同教育阶段对教育回报率的非线性影响，而假设每一年的教育是均质的。首先运用OLS估计扩展后的明瑟收入方程，来分析教育回报率的影响因素。然后通过0.15、0.5、0.85三个分位数回归进行分析，回归结果分别代表低收入群体、中等收入群体和高收入群体三类人群教育回报率的变动趋势，基本回归结果见表3。

表3 教育年回报率基本回归结果

注：*、**、***分别代表在10%、 5%和1%的水平上显著，括号内均通过Bootstrap(重复100次)获得标准误。

从表3中可以发现，使用中位数回归得到的教育回报率与OLS的回归结果相似，并且在分位数回归中，0.85分位数回归得到的教育回报率最低，0.15分位数上得到的教育回报率最高。这意味着，在所有年份的数据中低收入群体更能通过教育提高自身收入。基本模型回归结果中工作经验的系数显著为正，工作经验的二次项数为-0.001，在百分之一的水平上显著，说明工作经验对于收入而言有正向效应，但其边际效用是递减的，这与我们的预期相符。在OLS的回归分析中，性别虚拟变量的系数为0.350且在百分之一水平下显著为正，也就是说，男性相比较于女性而言，在其他条件不变的情况下，工资收入高出35%，分位数回归的结果与此差异不大。

以上分析是将所有年份作为混合截面数据从而得到了中国20世纪90年代到21世纪初这一时期教育回报率的笼统结果。为了进一步分析在这一期间中国教育回报率的变动趋势，本文根据年份进行分组回归来探究其变动趋势，也尝试用时间虚拟变量与受教育年限的交互项加入模型中来探究变动趋势，交互项的系数即为相比较于基准年(1991年)教育回报率的增减变动百分比。引入交互项的好处在于不会损失样本量，但它会使模型变得复杂，出现了严重的多重共线性问题，造成大量偏回归系数不显著。由此得到的教育回报率变动趋势情况如图1，从图1中可以看出，教育回报率在2004年以前有显著上升趋势，而在2004年以后整体教育回报率不再保持原有的上升态势，并且在2006～2011年和2013～2014年出现了下降的新趋势，2016年又上升到2004年的教育回报率水平，这与邓峰等[18]用CHNS数据估计出来的1989～2004年趋于上升、2006年开始下降的结论大体一致。教育年回报率前期的不断上升，是因为改革开放后中国劳动力市场分割被打破、流动性不断增强以及市场经济中产权得到界定和保护，促使受教育者得到更充分的激励；教育年回报率在2006年后出现的增速放缓甚至下降趋势，则是因为随着改革开放的进一步深入，市场对教育的激励作用增速减缓，加之义务教育阶段的普及和高等教育扩招，造成劳动力市场供大于求局面，使得教育年回报率呈现下降趋势。

在分位数回归中，代表低收入群体的年教育回报率趋势线始终高于代表中等收入群体的中位数回归，代表高收入群体的教育年回报率有小幅上升。不过，2016年的回归结果显示中低收入群体的教育回报率依然呈增长趋势，增长率还略高于高收入群体。由此可见，低收入群体更能通过勤奋学习来提高个人收入，教育无论是在改革开放初期还是近几年都起到了提高社会群体流动性和保障社会稳定的作用。

图1 教育年回报率变动趋势

2.教育年回报率的地区性差异

我国各地区经济发展水平差异大，义务教育普及与高等教育扩招政策也是分地区、分批次推行的。图2是使用所有年份数据求得的各地区在OLS和分位数回归方法下的偏回归系数教育回报率。在OLS回归方法下，2011年之前中部的教育回报率最高，东部的教育回报率最低。但是2011年之后的教育回报率东部地区均高于中部地区，而西部地区教育回报率在2011～2014年间总体呈现出不断增长的趋势。有关地区差异对教育回报率的影响没有定论，2004年以前大多认为教育回报率西部地区至少不低于东部地区[8]，但是此后杨穗[28]利用2005年1%人口抽样数据得出，东部地区的教育回报率比中部地区高出1.07%，而西部地区最低。教育回报率的地区差异及其趋势变动的原因，有以下几种可能：①所采用的样本在每个地区搜集的比例不一致，尤其是当各个年份在各地区的样本采集数量不一致时，可能会造成结果不准确；②各个地区生产技术条件、对劳动力的要求不同而导致这种差异。东部地区的经济发展水平高于中西部地区，但其教育回报率在2011年以前却是最低的，这可能与对外开放初期东部地区发展以需要廉价劳动力的外贸型经济为主有关，在2011年以后，随着东部地区制造业的升级，对高等教育人才需求增加，东部地区教育回报率也不断上升。而随着一带一路倡议的实施，使得西部地区对高等教育人才的吸引力变大，因而西部地区教育回报率也在上升。与东部地区相比较而言，中部地区和西部地区教育水平较低，因而在早期教育回报率高于东部地区，但是随着中西部地区教育水平与东部地区差距逐渐缩小，中部地区的教育回报率也有所下降。

本文也对东部、中部和西部地区的教育回报率进行了分位数回归，从图2中可以发现，中高收入群体的教育回报率回归结果相比较于OLS回归的地区之间的差异相对较小，而地区间的差异更多体现在低收入群体。中部地区低收入群体的教育回报率在2011年以后下降幅度远超其他收入群体，这与中部地区人口众多、经济发展水平相比东部地区较低、大量受过教育的个人难以找到报酬丰厚的工作岗位有关。东部地区高收入群体的教育回报率近年来增长态势也要强于其他收入群体，同样是存在众多人口的东部地区，却因为经济发展水平高，拥有良好教育的劳动力能够找到收入高的工作岗位，所以东部地区高收入群体的教育回报率近年来呈现更快的增长趋势[29]。

图2 东中西部地区教育回报率变动趋势比较图

3.教育年回报率的城乡差异

早期城市教育回报率高于农村教育回报率这一结论被普遍接受[30-31]，为探究城乡教育回报率近年来变动趋势，本文在OLS的基础上还进行了分位数回归，图3是城乡教育回报率的趋势对比分析图，从图3中可以发现，无论是OLS回归还是分位数回归，城市的教育回报率均显著高于农村,这与学界共识一致。2006年之前城市和农村的教育回报率都呈现出显著增长趋势，2006年以后增长趋势放缓，个别年份出现下降趋势，这与前文分析的整体变动趋势也是一致的。但是到2012年以后，城乡之间教育回报率的差异发生了逆转，农村教育回报率大幅提升，考虑到本文合并数据库的特殊性，2011年以前使用的是CHNS数据，2011年以后则使用了其他数据库，但2012年、2014年和2016年均使用了CLDS数据，仅仅是比较这三年的数据，也可以发现农村的教育回报率有了显著提升，而城市的教育回报率稳步不前，甚至略有下降。其中农村低收入群体教育回报率增长幅度最大，农村中等收入群体增长幅度次之，农村高收入群体教育回报率增长幅度最小。造成这种趋势的原因如下：①早期城市的教育回报率高于乡村，主要是由于城乡二元体制造成受过教育的农村劳动力难以找到报酬丰厚的工作岗位[18]；②2012年后，随着城乡户籍制度改革，农村劳动力人口更方便进入城市寻找工作以及中国人口数量红利开始逐渐消失，拥有初级和中等教育水平的农村低收入群体在城市中的劳动报酬不断提升，其教育回报率大幅度上升。

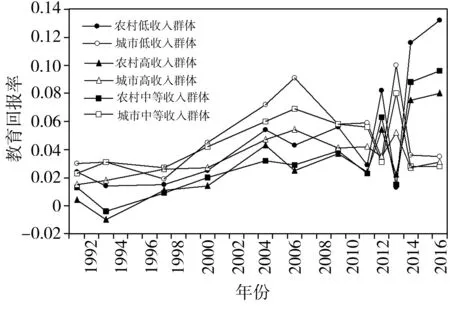
图3 城乡教育回报率趋势比较

4.教育年回报率的性别差异

不同性别个体的年教育回报率存在差异，其变动趋势见图4，从图4中可以发现，女性教育回报率普遍高于男性，在2006年以前两者都呈现出波动上升的趋势，而在2006年以后这种增长趋势消失，与之前整体的、地区的、城乡的教育回报率变动趋势和情况相同。

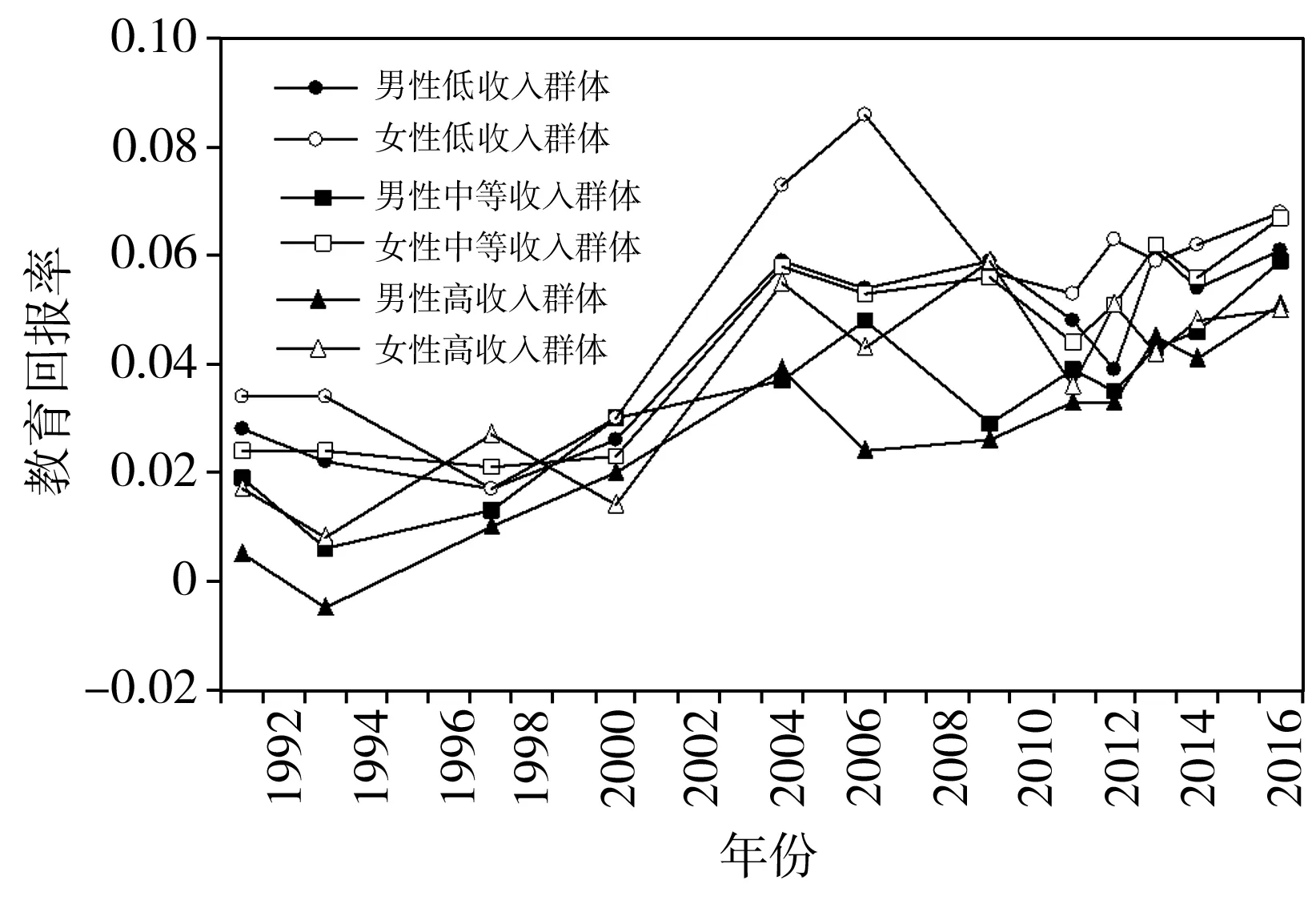
图4 教育回报率趋势的性别差异比较

(二)各阶段教育回报率分析

上文中对教育回报率变动趋势和影响因素的研究没有考虑到不同教育阶段对收入的回报效应是非线性相关的，下面将把最高学历这一类别变量作为解释变量，探寻各个阶段教育回报率的变动趋势。

1.初等教育回报率

本文将小学阶段和初中阶段，统称为初等教育阶段。初等教育回报率的回归结果如图5，尽管大多数偏回归系数均不显著，但仍可以从1991年、2004年和2012年中的OLS偏回归系数中发现初等教育回报率存在先升后降的趋势，系数不显著与下降的趋势可能是由于1994年在全国普及义务教育导致的[32]。2004～2012年教育回报率有一个剧烈下降，结合我国九年义务教育的普及，就个人而言，8岁入学、18岁成人后进入劳动力市场，2004～2012年恰好处于第一批九年义务教育个体进入劳动力市场时期，因而受到供求关系的影响导致教育回报率下降。供求关系主要是指到2004年以后，初等教育学历者供给大于需求；而相应的高等教育人才市场却十分紧缺，在下文关于中、高等教育变动趋势中可以发现，2004年中、高等教育回报率呈现突增态势。

图5 初等教育回报率变动趋势

2.中等教育回报率

中等教育回报率的回归结果相比较于初等教育显著性有大幅提高，图6是中等教育回报率的变动趋势图，从图6中可以发现，从2009年之后教育回报率呈现明显下降趋势，一方面这与丁小浩等[33]发现中等教育回报率(高中)从2002年的13.89%下降到了2009年的13.21%的结论相佐证，另一方面回归结果还证实中等教育回报率在2012～2014年进一步下降，尽管2016年相比2014年有小幅上升，但原有大幅增长态势已经消失。分位数回归研究发现，在1993～2000年间，低收入群体的教育回报率呈下降趋势，而高收入群体的教育回报率却呈现不断上升趋势，由此可知，这一时期是我国社会群体流动性变差、教育稳定器作用减弱的一个时期。此外，2014年以后中等教育回报率在不同收入群体之间的差距大幅缩小这一新的趋势出现。

图6 中等教育回报率变动趋势

3.高等教育回报率

高等教育回报率一直是社会关注的热点问题，尤其是近年来大学生就业难与社会热衷于上大学的现象并存。1999年开始的大学生扩招导致高等教育学历人数不断增加，高等教育回报率的变化为学界所关注。杨素红等利用CHNS1991-2011的数据分析研究认为，高等教育溢价效应在2000年以后显著下降[27]；但方超采用CHIP1995和CHIP2013两期截面数据分析研究得出，大学本科的教育回报率在1995～2013年增长了三个百分点，而同期研究生的教育回报率则有所下降[34]。对于这两个相互矛盾的结论，有必要在更长的时间跨度上来考察高等教育回报率的变动趋势。

高等教育回报率的年份分组回归结果统计显著性很好，使用OLS回归和分位数回归，得到高等教育变量的偏回归系数即高等教育回报率，其变动趋势如图7所示。从图7中可以发现，2004年以前高等教育回报率呈显著上升趋势，但是在2004年以后增长趋势消失甚至个别年份高等教育回报率在下降。如前所述，造成这一现象的原因可能是，高等教育实行扩招后的首批大学生、研究生进入劳动力市场，造成供大于求的局面，从而使得高等教育回报率下降。这与杨素红等得出的高等教育回报率变动趋势开始下降主要体现在2000年以后(相比本文研究得出的下降趋势主要体现在2004年，开始下降的年份由于模型中选取的控制变量不同而稍有差异)但是后期不再上升的结论是一致的。

图7 高等教育回报率变动趋势图

4.影响因素中考虑不同教育阶段的异质性

探讨城乡间不同等级的教育回报率情况，OLS回归以及分位数回归结果如表4所示。从表4中可以发现，城市教育回报率远高于农村。其中，在义务教育阶段，同样取得初等教育水平的个体，城市个体的教育回报率是农村个体的2.015倍；在中等教育阶段，城市个体的教育回报率是农村个体的1.826倍；在高等教育阶段，城市个体的教育回报率是农村个体的1.516倍。尤其值得注意的是，在高等教育回报率中，城市低收入群体教育回报率高于农村低收入群体，但农村高收入群体教育回报率却高于城市高收入群体，这意味着城乡因素对高等教育回报率的影响在高收入群体和中低收入群体中差异较大。

表4 城乡各教育阶段教育回报率对比

注：*、**、***分别代表在10%、 5%和1%的水平上显著。

目前，学界普遍认为女性的教育回报率普遍高于男性[8]，但现有对教育回报率性别差异的分析，大多是将受教育年限作为因变量，较少考虑教育的异质性问题。表5是将所有年份的数据分为初、中、高等三个教育层次进行分析。OLS回归中，各个教育阶段下，男性的教育回报率均高于女性的教育回报率，该结果与现有女性教育回报率高于男性的结论不同。我们发现，只有在低收入群体中，女性的教育回报率才在各个教育阶段高于男性，这意味着社会应当更加关注那些低收入群体的女性教育问题。

表5 性别的各阶段教育回报率对比

注：*、**、***分别代表在10%、5%和1%的水平上显著。

(三)内生性问题与稳健性检验

在研究教育回报率变动趋势时，最严重的内生性问题便是遗漏能力变量和家庭背景变量。个体能力对个体收入和个体接受教育都有影响，一方面一个能力强、智商高的人读书更轻松、更愿意选择去获取高学历，另一方面凭借着天生的能力优势也会使其在工作中获得更高的收入；个体拥有更好的家庭背景，一方面在物质生活和家庭氛围中更有利于其学习和追求更高的学历，另一方面在找工作中也更容易找到高薪职业。从此可知，由能力遗漏变量和家庭背景遗漏变量引起的内生性问题将会使得教育回报率被高估。分位数回归相比较于OLS的均值回归方法，可以对收入不同分位点的群体进行分别回归讨论，由于不同收入群体涵盖了不同的能力和家庭背景变量，可以在一定程度上减轻内生性问题。对此，考虑到数据的可获得性，本文用CGSS2013的数据对OLS和分位数回归下的内生性问题进行检验。得到的回归结果如表6所示，其中控制的遗漏变量有两个，一个是用来代表个体能力智商的配偶受教育水平，这是基于人们总是和自己能力相近的人结合在一起即门当户对的假设，二是用父亲的社会地位来代表家庭背景这一遗漏变量。表6中的数值为该回归结果下的教育回报率取值，括号内的数字是系数的标准误。从表6中可以清晰地看出，控制遗漏变量后，OLS回归结果、代表低收入群体的0.15分位数回归结果和代表高收入群体的0.85分位数回归结果都下降了，关于内生性问题的存在会高估教育回报率的猜想是正确的。同时我们注意到，代表中等收入群体的0.5分位数的回归结果相比较于OLS的回归结果而言，是否控制遗漏变量对系数影响不大，也就是说，相比较于传统的OLS回归，分位数回归的结果在一定程度上可以缓解内生性问题。控制遗漏变量的前后，低收入群体得到的教育回报率均高于高收入群体，也证明前文中关于不同收入群体教育回报率比较的分析结果是稳健的。

表6 教育回报率稳健性分析

注：*、**、***分别代表在10%、 5%和1%的水平上显著，括号内为标准误。

六、结论

现有对中国教育回报率变动趋势的研究，在数据上采用时间跨度较短的微观数据库，不能较好地反映长期趋势；在研究方法上多采用OLS回归方法，具有一定的研究局限性。本文使用CHNS、CLDS和CGSS合并后的1991～2016年的数据，使用分位数回归方法分别对均质的年教育回报率、地区和城乡教育回报率以及异质的不同教育阶段回报率变动趋势和影响因素进行了分析，在不损失样本量的情况下缓解了部分因遗漏个人能力、家庭背景而造成的模型偏误问题。同时分位数回归代表的收入差异，也使得原有单一的个人教育回报率变动趋势，被细化为高收入群体、中等收入群体、低收入群体的个人教育回报率变动趋势，使分析结果更具有现实解释力。

通过对1991～2016年数据的分析，可以发现，中国年教育回报率的总体变动趋势在2004年前教育回报率呈显著上升趋势，之后教育回报率增长趋势放缓，甚至个别年份出现下降趋势。分地区来看，东部地区的教育回报率在2011年前是最低的，2011年后其教育回报率不断上升；分城乡来看，城市教育回报率显著高于农村；分性别来看，中等收入群体和高收入群体下，男性的教育回报率均高于女性的教育回报率，只有在低收入群体中，女性的教育回报率在各教育水平阶段均高于男性。

针对中国教育回报率变动的研究，我们认为要进一步提高教育的回报率和公平性，第一，在经济发展的同时，重视教育数量型资源和质量型资源的投入，逐步提高全国劳动者的受教育年限；第二，解决教育资源的地区性和城乡之间不均等问题，通过转移支付和教育质量提升使得地区之间和城乡之间的教育资源更加均等化，使得中西部地区和农村地区的劳动者通过提升人力资本获得更合理的收入；第三，重视对女性的教育，尤其是要提高低收入群体的中西部地区和农村地区女性的教育水平，使得更多的适龄女性能够接受更好和时间更长的教育，提高教育中的性别平等度。

注释：

①CHNS(China Health and Nutrition Survey),中国家庭健康营养调查。

②CLDS(China Labor-force Dynamics Survey),中国劳动力动态调查。

③CGSS(Chinese General Social Survey),中国综合社会调查,始于2003年，是我国最早的全国性、综合性、连续性学术调查项目。CGSS系统全面地收集社会、社区、家庭、个人多个层次的数据，总结社会变迁的趋势。

④CHIP(Chinese Household Income Project Survey)，中国家庭收入调查。

⑤ CULS(China Urban Labor Survey)，中国城市劳动力调查，是由中国社会科学院负责组织实施的一项大规模城市家庭抽样调查项目，2001年启动首轮调查，每五年开展一次。该调查旨在全面动态了解城市家庭生活、就业和社会保障状况，通过严谨规范的科学研究为政府相关政策制定提供依据。