基于加权双剪强度理论的高强井壁结构理想弹塑性解

(安徽理工大学 土木建筑学院，安徽 淮南 232001)

1 研究背景

厚壁圆筒结构因受力合理而广泛应用于地下结构工程。井壁与土体共同作用，厚壁圆筒结构不仅受到水平地应力、冻结压力[1]，而且还受到疏水沉降造成的竖向附加力和井壁自重应力[2],因此立井井壁是在围压和轴压共同作用下工作的。

针对薄壁圆管和厚壁圆筒的弹塑性解， 国内外学者进行了大量研究。 Heitzer[3]采用数值计算程序对内压、 轴压共同作用下的缺陷圆管的塑性极限承载力进行了倒塌分析， 实际上并没有给出真正意义上的极限承载力公式。 Stokey等[4]基于Mises屈服准则， 推导出薄壁圆管和厚壁圆筒在内压、 弯矩、 轴力和扭矩共同作用下的极限承载力， 但得出的结果偏保守。 郑津洋[5]基于理想弹塑性材料假设和Mises屈服准则， 给出仅受内压作用下厚壁圆筒的弹塑性应力表达式和塑性区半径与内压的关系。 朱国民等[6]基于理想弹塑性材料假设和Von-Mises屈服准则, 给出了在内压和轴向力共同作用下的厚壁圆筒极限承载力公式。 余同希[7]基于Tresca屈服准则和Ludwik理论并考虑了主应力大小的影响， 给出了理想弹塑性材料和强化材料的厚壁圆筒在内压作用下的弹塑性应力解。 侯公羽等[8]基于Levy-Mises本构关系及 D-P 屈服准则给出了轴对称圆巷理想弹塑性应力解和塑性区半径表达式， 但对主应力大小考虑不够全面。 冯剑军等[9]则基于双剪统一强度理论， 系统讨论了不同中间主应力效应， 得出厚壁圆筒在内压与轴向力共同作用下的塑性极限载荷表达式， 其不足在于仅考虑轴压作用对σz的影响而忽略内压作用对σz的影响。 李雪梅等[10]基于三参数强度准则推导了流固耦合作用下立井井壁弹性区和塑性区的应力解析表达式， 其不足在于仅考虑水平荷载对井壁结构应力解的影响。

虽然针对厚壁圆筒在围压作用下的弹塑性解较多， 但采用的计算模型并不能完全描述立井井壁的受力状态， 同时以上塑性分析大都采用 Mises屈服准则和Tresca屈服准则， 这2种准则主要适用于金属类材料。 为此， 本文将建立符合井壁结构实际受力的力学模型， 采用更加适用于混凝土材料的加权双剪强度理论， 充分考虑不同中间主应力效应求解立井井壁极限承载力， 以此来优化井壁结构， 最大程度发挥材料的潜力， 创造更大的经济效益。

2 加权双剪强度理论

双剪统一强度理论不仅能够体现材料的拉压异性和同性特征，考虑不同中间主应力效应，还能够适用于不同的屈服准则[9],如在岩土工程中，采用轴心抗压强度σc和主应力形式的双剪统一强度理论来表达屈服准则[11]，即：

(2)

式中：b(0≤b≤1)为反映中间主应力影响的权系数，当b取不同的值时 ,双剪统一强度理论就成为不同的强度准则；α为轴心抗拉强度σs与轴心抗压强度σc之比。

对于岩土类材料，当权系数取b=1/2时，双剪统一强度理论就成为加权双剪强度理论，即：

双剪统一强度理论的优点在于考虑了岩土类材料中间主应力的影响,又可以与很多材料的真三轴试验结果相符合[12]。

3 弹塑性求解的几点假设

(1)假设外压和轴压的加载顺序对厚壁圆筒的极限承载力影响不大，文献[6]对这一假设用有限元数值解给予了验证。

(2)假设材料是均匀的、各向同性。

(3)假设材料不可压缩，故根据Levy-Mises本构关系有

(5)

其中εz=0，dεz=0，则有2σz-σr-σθ=0，所以有

σz=(σr+σθ)/2 。

(6)

4 外压p0和轴压P共同作用下厚壁圆筒弹塑性解

对于内半径为R0、外半径为R1、塑性区半径为Rc的厚壁圆筒，同时承受内压p1和外压p0作用时，其弹性应力解可由拉梅(Lame)[13]公式式(7)表示。

(7)

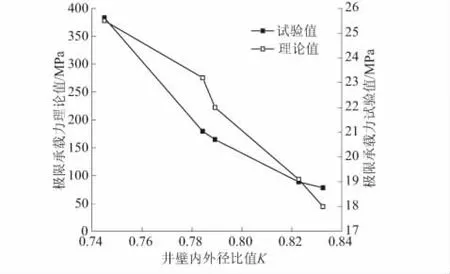
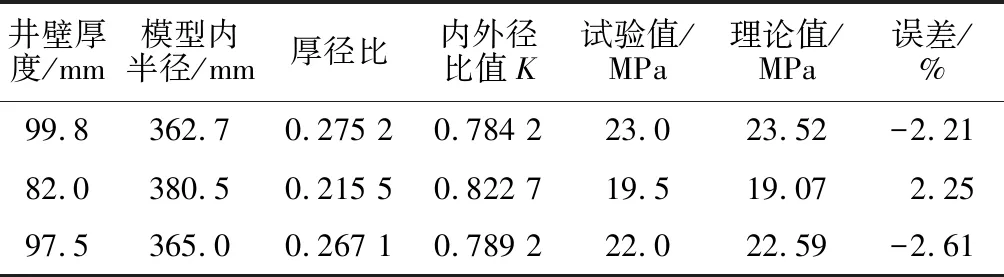
式中r为圆筒半径，其值范围为R0

若圆筒内外径比用K=R0/R1表示，塑性区半径与外径比值Kc=Rc/R1，则厚壁圆筒仅在外压作用下的弹性应力解可由式(7)和式(6)联立得到，即

(8)

由于假设材料不可压缩，可认为轴压不影响由内压所引起的厚壁圆筒环向应力和径向应力分布，故轴压引起的竖向应力表达式为

(9)

那么厚壁圆筒在外压和轴压共同作用下弹性应力表达式为

(10)

假设拉为正，压为负，由于轴力是压力，所以σr，σθ，σz之间的关系有3种情况：σr≥σz≥σθ,σr≥σθ≥σz,介于σr≥σz≥σθ与σr≥σθ≥σz之间。

4.1 在σr≥σz≥σθ的情况下求圆筒弹塑性应力解及其极限载荷

令σ1=σr，σ2=σz，σ3=σθ，其边界条件为：当r=R0时，σr=0；当r=R1时，σr=-p0。此时σz≤(σr+ασθ)/(1+α)成立而σz>(σr+ασθ)/(1+α)不成立。将式(10)代入式(3)可得

又因为σz≥σθ，所以有

(12)

将式(11)代入式(10)并联立式(9)得

(13)

令r=R0可得弹性极限轴力为

(14)

令r=R1可得塑性极限轴力为

(15)

令r=Rc可得塑性区半径与外压和轴压的关系为

将式(11)代入式(10)得塑性区应力表达式为

(17)

那么当Rc≤r≤R1时，圆筒受内压pc和外压p0，故弹性区应力表达式为

4.2 在σr≥σθ≥σz的情况下求圆筒弹塑性应力解及其极限载荷

令σ1=σr，σ2=σθ，σ3=σz，其边界条件为：当r=R0时，σr=0；当r=R1时，σr=-p0。

4.2.1σθ≤(σr+ασz)/(1+α)情况下

按照4.1节将式(10)代入式(3)可得：

(20)

(21)

(22)

令r=R0可得弹性极限轴力为

(23)

令r=R1可得塑性极限轴力为

(24)

令r=Rc可得塑性区半径与外压和轴压的关系为

将式(20)代入式(10)可得塑性区应力表达式为

(26)

同理可得弹性区应力表达式为

(27)

4.2.2σθ>(σr+ασz)/(1+α)情况下

将式(10)代入式(4)可得

(28)

(29)

令r=R0可得弹性极限轴力为

(31)

令r=R1可得塑性极限轴力为

令r=Rc可得塑性半径与外压和轴压的关系为

将式(28)代入式(10)可得塑性区应力表达式为

(34)

同理可得弹性区应力表达式为

(35)

4.3 在(σθ)min≤σz≤(σθ)max的情况下求圆筒弹塑性应力解及其极限载荷

因为σθ沿半径方向是随着r的增大而逐渐增大的，当R0≤r≤r0(r0为判定σθ和σz大小的圆筒半径值)时，三维应力之间关系为σr≥σz≥σθ；当r0

当R0≤r≤r0时, 在σr≥σz≥σθ的情况下，只有σz≤(σr+ασθ)/(1+α)成立，而σz>(σr+ασθ)/(1+α)不成立。从而按以上同样的方法,可求得

(36)

(37)

(38)

(39)

其弹塑性应力解同本文4.1节解，所不同的是R0≤r≤r0,σc满足式(37)。

当r≥r0时, 在σr≥σθ≥σz的情况下，只有σθ≤(σr+ασz)/(1+α)成立而σθ>(σr+ασz)/(1+α)不成立。从而按以上同样的方法,当r0≤r≤R1时，可求得：

(40)

(41)

(42)

其弹塑性应力解同本文4.2.1节的解，所不同的是r0≤r≤R1，σc满足式(41)。

5 厚壁圆筒仅在外压p0作用下厚壁圆筒弹塑性解

由于假定岩土材料不可压缩σz=(σr+σθ)/2，所以仅在外压作用下只有σr≥σz≥σθ，此时只有σz≤(σr+ασθ)/(1+α)成立而σz>(σr+ασθ)/(1+α)不成立。现令σ1=σr，σ2=σz，σ3=σθ，并将其代入式(3)可得

(43)

将式(43)代入平衡方程，则

(44)

可得

(45)

对式(45)积分得

(46)

将边界条件r=R0时，σr=0代入式(46)可得

(47)

将式(47)代入式(46)，并考虑式(6)、式(43)可得塑性区应力为

当Rc≤r≤R1时，圆筒受内压pc和外压p0，故弹性区应力表达式为

(50)

因弹性区内壁处于屈服状态，令式(50)中r=Rc并代入式(3)可得塑性区半径与外压的关系为

(51)

圆筒开始屈服产生于圆筒r=R0处，当Rc=R0时，式(51)取得最小值，此为基于加权双剪强度理论的厚壁圆筒弹性极限围压，即

(52)

当Rc=R1时，式(51)取得最大值，此为基于加权双剪强度理论的厚壁圆筒塑性极限围压，即

(53)

6 分析与讨论

以上理论推导均是基于材料的均质性和各向同性假设，金属类材料各向同性程度高，岩土类材料均质性差，各向异性特征更为明显。因此，在外压作用下立井井壁模型破坏形式并非理想的由内到外逐层破坏[14]，而是会出现如图1所示的剪切破坏和压剪破坏。

图1 井壁模型试验破坏形式Fig.1 Damage patterns of shaft lining in model test

以上推导得到的极限承载力理论值和试验值存在差异，所以引入修正系数m(试验值与理论值之比)对极限承载力公式进行修正,修正后的极限承载力公式变为

(54)

文献[15]—文献[17]描述了立井井壁极限承载力模型试验，为了保证模型试验和理论模型具有相同的初始条件和边界条件，模型试验是在经过煤炭部门认定的高压加载装置中进行的，模型试件是在专门加工的模具中浇筑完成的，试件在养护一段时间后需要经过精密车床加工，保证端面的光滑度，使井壁能够发生径向变形。模型加载过程中，利用高压油泵对井壁模型施加围压来模拟井壁受到的外压作用，其竖向变形通过高强螺栓和盖板加以约束，所以试验全过程中模型基本处于平面应变状态。现从文献[15]—文献[17]中选取井壁强度全为C70、厚径比不同的5组井壁模型极限承载力结果列于表1。根据文献[18]中关于高性能混凝土拉压比试验的结果，对于C70混凝土，1/α=12.8。将表1中相关参数代入式(53)即可得到井壁极限承载力的理论值，同时可求得相应修正系数m。

表1 井壁极限承载力试验值与理论值
Table 1 Experimental and theoretical values of ultimatebearing capacity of shaft lining

组号井壁厚度/mm模型内半径/mm厚径比内外径比值K试验值/MPa理论值/MPa修正系数m1118.0344.50.342 50.744 925.5382.910.067 0299.8362.70.275 20.784 223.2179.610.129 2397.5365.00.267 10.789 222.0164.690.133 6482.0380.50.215 50.822 719.188.680.215 4577.5385.00.201 30.832 418.078.170.230 3

将表1中井壁结构的试验值与理论值绘于图2，可以看出随着井壁内外半径比值K增大，理论值与试验值均呈减小趋势，说明理论推导的合理性。试验值与理论值差值较大，主要是由于井壁破坏形式宏观上表现为剪切和压剪破坏，而非理论上的由内到外逐层压坏。修正系数不断增大，是由于井壁厚径比不断减小，在围压作用下厚径比大的混凝土井壁各向异性程度低，厚径比小的混凝土井壁各向异性程度高。

图2 井壁极限承载力试验值与理论值比较Fig.2 Comparison of ultimate bearing capacity ofshaft lining between experimental and theoretical values

根据表1中的井壁内外径比值K和修正系数m作出修正系数曲线，并对曲线进行拟合，拟合情况如图3所示，拟合系数R2=0.993 4表明拟合程度很好。

图3 修正系数拟合曲线Fig.3 Fitted curve of correction coefficient

拟合方程为

m=6.629 06eK-12.674 77K-4.454 65 。(55)

将式(55)代入式(54)便可得到修正后的强度为C70井壁极限承载力为

P′=(6.629 09eK-12.674 77K-4.454 65)·

(56)

为了验证式(56)的正确性，现取文献[19]中的3组C70井壁模型加载数据列于表2，将表2中相关数据代入式(56)得到的修正井壁极限承载力理论值也列于表2。

表2 试验值与修正后理论值对比Table 2 Experimental values and corrected theoreticalvalues

由表2中试验值与修正后的理论值对比可知，其误差在±3%左右，误差较小，由此验证了式(56)的正确性，且式(56)参数少、计算方便,因此式(56)的计算结果对C70井壁模型试验结果具有指导意义。

7 结 论

(1)基于加权双剪强度理论，考虑不同中间主应力效应，推导了厚壁圆筒在外压p0和轴压P共同作用下的弹塑性轴压极限承载力公式。从轴压极限承载力公式可以看出：其大小与外压p0和材料的极限压缩强度σc有关，σc越大，p0越小，圆筒的轴向极限承载力越大。

(2)基于加权双剪强度理论与应力平衡方程，并考虑了材料的不可压缩，推导了σz为中间主应力时，厚壁圆筒在外压p0作用下的弹塑性极限承载力公式。从极限承载力公式中可以得到：圆筒的弹塑性极限承载力大小与σc成正比，与内外径比K成反比，所以，工程应用中井筒安全厚度要依据工程实际进行设置。

(3)修正后的强度等级为C70的井壁结构极限承载力理论值与试验值误差在±3%左右，验证了修正公式的合理性。对于其他强度等级的混凝土井壁只要有确定的拉压比α和相关试验数据，依照本文中方法也可得到其修正极限承载力公式。