基于模糊PID的电动汽车充电控制系统研究
2019-05-15葛笑寒
葛 笑 寒
(三门峡职业技术学院 电气工程学院,河南 三门峡 472000)
0 引言
电动汽车是以电能作为系统动力源,从蓄电池电源获得能量,驱动电机运转,属于能够遵守城市道路法规安全行驶的车辆,系统以电能为动力,可以实现行驶中废气“零排放”[1].目前电动汽车大部分都使用铅蓄电池和锂电池,采用恒压或恒流的充电方法,在充电过程中会出现过充、欠充等问题.
充电控制如果实行修正PID(Proportion,Integral,Differential)控制,则能基本满足充电过程控制[2],但是没有考虑充电过程电池组电压、电阻和相关参数的变化因素.充电过程的矢量控制虽然能够较好地实现充电流程控制,但是控制结构复杂[3].电动汽车充电过程的复杂性和蓄电池的非线性和多参量特征,常规PID控制策略已不能实现最优充电曲线.模糊自适应控制能够适应控制对象的非线性和迟滞性,且具有高鲁棒性.电动汽车在充电过程中应以常规PID为基础,增加模糊控制器,把系统最优响应和实际响应的偏差作为控制目标,把充电电压或者电流的误差和误差率作为输入,用模糊推理对PID的参数进行修正,保证电动汽车在充电过程中具有良好的静态和动态性能[4].本文采用模糊PID控制算法对电动汽车充电控制流程进行设计分析,并进行了系统仿真实验.
1 充电系统总体结构
充电系统的控制量主要为充电电流和电压,执行机构主要是人机交互设备、计量设备等.系统应对充电过程的电流和电压进行调控,帮助电动汽车实现平稳充电,防止出现过充、欠充或者损坏电池的现象.
充电系统总体结构如图1所示,其中,U、V、W为三相交流电源;PWM为脉冲宽度调制电路,用来产生脉冲信号,驱动电子开关运行.系统工作原理如下:三相交流电经过三相不可控整流器或者三相全桥整流滤波后得到恒定的直流电压,再经过直流变换器后,平滑滤波,最终将直流电能传送给电动汽车的动力电池.在功率转换过程中,根据输出电流、电压、电池管理系统传送的电池参数来控制电路输入,经过前端电路和集成芯片的处理,结合控制策略产生直流功率变换控制信号.
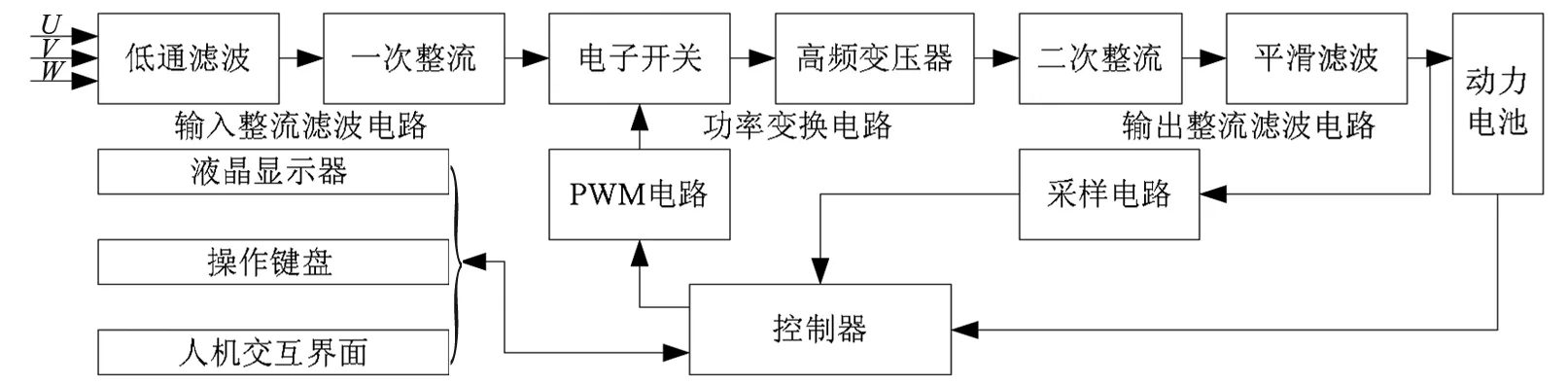
图1 充电系统总体结构示意图
2 电压电流模型构建
三相电压的变化量很大,难以进行有效调整,因此通常将功率电路和蓄电池一起作为被控对象.蓄电池的变化非常复杂,是一个非线性系统.建立电压电流理想化模型,相当于大电容与小电阻串联,功率变换电路等效为电感.考虑延迟环节的影响,系统传递函数可以看做有延迟函数e-TS存在,其中,e为常数;S为复变量;T为滞后时间.
系统电压和电流的开环传递函数分别为[5]:
(1)
(2)
其中,R为系统等值电阻;Ui(S)为功率电路理想输出电压;L为功率电路输出电感;I(S)为电池充电电流;C为电容;Uo(S)为电池充电电压.
3 模糊PID设计
充电控制需要对蓄电池的充电电压和电流进行控制也需要对充电中断和完成情况进行判断,并进行充电模式的转换.系统能够通过电压和电流的误差信号,适时调整PID参数,实现稳定快速运行.为此,考虑将模糊控制算法和传统PID算法相结合,采用模糊PID控制算法设计模糊控制器.
3.1 模糊控制器的建立
充电模糊控制器的输入是电压或者电流的误差a和误差变化率da/dt,误差变化率用ac表示,输出量为PID的比例(Kp)、积分(Ki)和微分(Kd)控参数,建立一个二维模糊控制器,其结构原理见图2.Ka,Kac为量化因子,Ku为决策因子.量化因子将输入量的精确值转换到模糊子集的论域,决策因子将解模糊后的控制量转换到基本论域中.模糊控制器的控制效果受Ka,Kac,Ku的制约.量化因子Ka等同于PID中的比例系数,Kac的作用等同于积分环节.实际控制过程中,需要通过调试或者仿真的方法确定决策因子和量化因子.

图2 二维模糊控制器原理示意图
3.2 模糊化计算
在电流控制环节,输入量为电流的误差a和误差变化率ac,输出量为PID控制器的控参数.模糊化的电流误差和误差变化率的计算如下:
a(n)=it(n)-i(n).
(3)
ac(n)=a(n)-a(n-1).
(4)
其中,it(n)为给定电流参考值;i(n)为实测电流值.
设误差a和误差变化率ac的输出变量的论域都为{-6,6},相应的模糊语言集为{NB,NM,NS,ZO,PS,PM,PB}.在保持系统稳定性的前提下,选择简单高效的三角函数作为输出变量,提高系统的动态响应.
3.3 建立模糊规则
要想得到快速响应和稳定精度,需要制定合理的模糊规则表.其目的是根据误差和误差变化率的变化,找到实际响应和最优控制间的差距.通过PID控制器的控参数进行修正,以达到控制要求[6].自整定规则如下:
(1)比例控制用来减小误差,Kp越大,系统响应越快;但是超调量也会随之增大.因此,在控制后期,比例值不宜过大.
(2)积分控制虽然能消除静差,但存在滞后性.开始时Ki小些,后期慢慢增大,以减少静态误差.
(3)微分控制能加速系统响应速度,但过大容易产生振荡,因此后期应逐渐减小,保证系统稳定运行.
3.4 解模糊
从模糊集合转换到实际输出的过程称为解模糊.该过程中,需要根据某时刻a和ac的函数隶属度曲线,经过模糊化得到精确的PID控制器的校正量隶属度[7].在模糊推理中选择模糊推理(Mamdani)型算法,解模糊采用重心法.推理和合成规则分别为Min法和Max法,输出即为PID参数的修正值.模糊后的PID参数计算公式为:
(5)
(6)
(7)
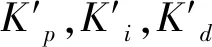
4 直流充电流程设计与仿真
4.1 模糊化的充电控制流程设计
模糊化的充电控制流程如图3所示.系统首先采集蓄电池的电流、电压信号,并与电池本身的参数进行比较,以判断蓄电池的充电阶段,并根据电池电流的大小,确定采用恒定电流控制还是恒压控制.恒流或恒压控制以实际电流或者电压值与参考值的误差和误差变化率为输入量,恒流充电时,采集恒流充电电流值;恒压充电时,采集恒压充电电压值.采用电压环和电流环的模糊PID控制,计算系统输出占空比.

图3 模糊化的充电控制流程示意图
4.2 模糊PID流程设计
以电压控制环节为例,进行模糊PID程序设计.在工业应用中,模糊自适应整定PID的参数能够进行在线调整.用C语言编程将会很复杂,根据模糊自适应PID控制系统的设计,可以把模糊控制器的仿真程序存入控制器存储器.运行时把误差和误差变化率作为输入量,实现对Kp,Ki,Kd的修正.系统流程结构如图4所示.根据模糊自适应系统输出的参量,可以得到输出控制量的计算公式为:
△u(n)=Kp*[a(n)-a(n-1)]+Ki*a(n)+Kd*[a(n)-2a(n-1)+a(n-2)].
(8)

图4 模糊PID控制流程结构图
4.3 系统仿真
设系统的电容为1000 F,电阻为0.015 Ω,电感为0.1 H.取时间常数0.01 s;量化因子Ka=Kac=0.01,比例、微分和积分环节的决策因子Ku分别为0.15,0.001,0.1;PID初始值Kp0=0.01,Ki0=0.00001,Kd0=1;设置采样周期为0.1 s.以电流环为例,最终的PID控制器模型为:

(9)
仿真中给定电流值12 A,在小信号的干扰下,仿真波形如图5所示,从波形图中看出,模糊PID稳定性能和动态性能大大提高,系统超调量也较小,系统具有较强的抗干扰性能.

图5 电流环波形仿真
5 结语
分析了电动汽车充电系统结构,确定了电压电流是主要的控制对象.建立了电动汽车直流充电的数学模型,分析得出了该系统的控制量电压和电流是带时滞扰动的二阶系统,采用模糊PID控制算法,设计了充电的电压和电流的模糊自适应PID控制器.对充电过程进行了流程设计.结果表明,该系统具有良好的动态性能,对电动汽车智能充电能起到良好的控制效果.
