对抗网络下多智能体系统的能控性分析
2019-05-15曹少斌纪志坚于海生
曹少斌 纪志坚 于海生 侯 婷
(青岛大学 自动化工程学院,山东 青岛 266071)
近年来,多智能体系统(MAS)的协同控制研究得到了广泛的研究,同时其研究成果已应用于工程学,生态学,生物学,社会学,计算机通信等许多领域.基于MAS的协同控制研究了许多基本的重要问题,包括一致性[1-3],不可控拓扑结构[4],开关拓扑[5-6]等.可控性是MAS协同控制的基础研究课题.MAS的可控性最初由Tanner[7]提出,其中一个智能体被作为领航者.基于最近邻居互连协议,提出了一个在固定时不变拓扑下拉普拉斯矩阵可控性的充分必要条件.据此,为MAS的可控性提供了一些充分/必要的条件.基于此,文献[8]提出了另一种代数条件.之后,研究人员从图论角度研究了MAS的可控性[9-10].具体来说,图划分的各种概念和性质被用来研究MAS的可控性,例如等价划分[11],几乎等价划分[12]等.最近,还研究了MAS在某些特殊图上的可控性.例如路图和环图[13],星图[14]等.因此,本文致力于解决MAS中对抗交互的能控性问题.首先,领航者-跟随者结构被引入到对抗网络中.接着,验证了Tanner(2004)提出的系统的必要条件和充分条件.结果表明,协作网络下的可控条件并不完全适合对抗网络,并给出了对抗网络能控的两个必要条件.最后,研究了对抗网络下Peterson图的能控性,并与协作网络下的能控性进行了对比,得到了Peterson图在协作网络下和对抗网络下能控性等价的部分情形,并将其应用到了Peterson图以外的三部图的情形下.
1 系统描述
考虑一个多智能体网络,假设网络中包含n个具有单积分器动态的智能体,顶点集为V=(v1,v2,…,vn).假设有m(m≤n)个智能体被选作领航者,每个领航者都赋给一个外部控制输入,其余智能体被选作跟随者.进一步假设,顶点集中的前m个顶点被选作领航者,即领航者节点集合为VL={v1,…,vm},跟随者集合即为VF=VVL.
对抗网络下,跟随者i∈VF服从以下共识协议:
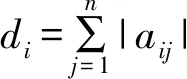
每个领航者i∈VL都赋给一个相应的外部控制输入ui且服从如下共识协议:
对抗网络下的系统动态方程可以表示为:
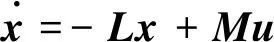
(1)

2 对抗网络下的领航者-跟随者结构
包含n个智能体的网络中,假设存在两种不同的智能体:一些严格服从共识协议,另一些可给定外部输入对其进行控制,这两种智能体分别称之为跟随者和领航者.在对抗网络系统(1)下,可以将系统方程重新写作如下形式:
(2)
其中Ll和Lf分别对应领航者和跟随者的编号,lfl表示从领航者到跟随者的通信连接关系,u为外界控制输入的迭加向量,xl和xf分别是所有领航者状态和跟随者状态的迭加向量.根据领航者-跟随者结构划分,上述系统可表示为:
(3)
研究对抗网络系统(1)下的能控性问题,就是研究对抗网络中领航者对跟随者的控制能力,即研究系统:
(4)
的能控性问题.
对于给定的拓扑图G,系统(4)是一个线性时不变系统,系统控制矩阵为:-Lf∈R(n-m)×(n-m),系统输入矩阵为:-lfl∈R(n-m)×m,与符号拉普拉斯矩阵L相关.当领航者只有一个时(即m=1),系统输入矩阵-lfl将退化为一个列向量.
则系统(4)的可控性矩阵为:
以上分析表明Tanner领航者-跟随者结构划分完全可以适用于对抗网络下能控性问题的分析,以下讨论中将沿用Tanner关于领航者-跟随者拓扑结构下的定义方式:
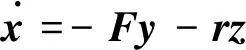
(5)
其中-F表示系统控制矩阵-Lf,-r表示系统输入矩阵-lfl,则系统(5)可控性矩阵为:
C=[-r,Fr,-F2r,…,(-1)nFn-1r]
因为无向图下矩阵L是对称的,因此矩阵F也是对称的.则存在矩阵U满足F=UDUT,其中矩阵U的列由矩阵F的相互正交的特征向量组成,矩阵D为元素由矩阵F的特征值构成的对角矩阵,则矩阵C可写作:C=[-r,UDUTr,-(UDUT)2r,…,(-1)n·(UDUT)n-1r].
可以简化为:C=[-r,UDUTr,-(UDUT)2r,…,(-1)n(UDUT)n-1r]=U[-UTr,DUTr,-D2UTr,…,(-1)nDn-1UTr].
由于矩阵U是非奇异的,所以只需考虑右半部分的秩:[-UTr,DUTr,-D2UTr,…,(-1)nDn-1UTr].
可知系统(-F,-r)与系统(-D,-UTr)有相同的能控性,则由PBH秩判据可得:
[siI+D,-UTr]
(6)
当式(6)对于矩阵-D的任意特征值都是行满秩时,即rank[siI+D-UTr]=n-m,系统可控.由于正交矩阵U是可逆矩阵,是满秩的,U的列向量都是线性无关的,则有rank(UTr)=rank(r).假设矩阵UTr的秩为p,即矩阵UTr有p行(列)线性无关,则当对角矩阵D中任意元素λ的重数超过p个时,取si=λ,则siI+D有大于p个零行,从而使得矩阵[sI+D-UTr]对于si=λ不满秩,则可知对角矩阵D中任意元素λ的重数不大于矩阵r的秩是系统可控的必要条件.
以上讨论结果可得到以下定理:
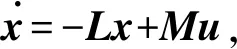
1)F的相同的特征值的个数不大于r的秩;
2)F的任一特征向量与r不同时正交.
3 对抗网络下的Peterson图
如图1(a)所示,Peterson图是由10个节点15条边构成的无向图.节点集V可以被划分为3个两两不相交的非空子集,并且使得任意一条边的两个端点都不在同一子集内,则称之为三部图.
基于三部图可给出Peterson图的一种划分如下:
π={{1,4,9},{3,6,7},{2,5,8,10}}
则相应的拉普拉斯矩阵可写作:
L=

对于划分π,其中V1={1,4,9},V2={3,6,7},V3={2,5,8,10}.矩阵C表示领航者-跟随者结构下的可控性矩阵.协作网络下的可控性矩阵记为CE:
CE=[-rE,FrE,-F2rE,…,(-1)nFn-1rE]
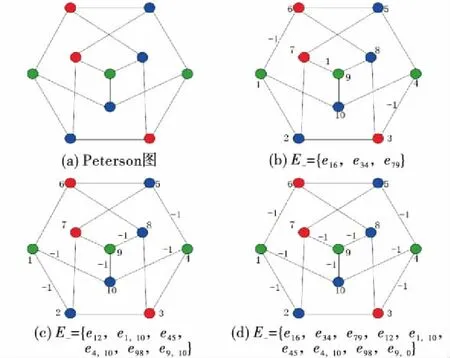
图1 对抗网络下的Peterson图及三部图
如图1(b)所示,将V1中所有节点选作领航者时,有:
F=

矩阵C和矩阵CE的秩分别为:
rank(C)=4,rank(CE)=4
类似地,如图1(c)所示,当选取V1中所有节点作为领航者,同样可以得到rank(C)=4,rank(CE)=4;当选取V3中全部节点作为领航者,可得到如上同样的结果.最后,如图1(d)所示,当选取V1中所有节点作为领航者时,可以得到同样的结果rank(C)=4,rank(CE)=4;当选取V3中全部节点作为领航者,可得到如上同样的结果.由此可以佐证引理1.当符号图G的节点集V可以被划分为两个互不相交的子集V1和V2,使得V1和V2之间的每条边都是负边,其余边都是正边,则图G是结构平衡的.
引理1[15]当交互对抗网络是结构平衡的.如果领航者选自同一子集,则系统(F,r)的能控性等价于系统(F,rE).
结合上述分析和引理1可以得到以下定理:
定理2当负边与领航者的选择满足以下两个条件时,对抗网络下的Peterson图的能控性等价于对应协作网络下的Peterson图的能控性:
1)选取V1和V2/V3之间的所有边都选作负边;选取V1或V2/V3中所有节点作为领航者.
2)选取V1和V2(或V1和V3)之间所有边作为负边;选取V1,V2和V3其中任一子集中所有节点作为领航者.
4 仿 真
例1:如图2所示的对抗网络下,符号完备图包含5个节点,拓扑图中存在3条负边,分别为e13,e23,e24,其余皆为正边,其中E-={e13,e23,e24}.

图2 五阶符号完备图
取节点1和节点2作为领航者,则符号拉普拉斯矩阵L和控制输入矩阵M分别为:
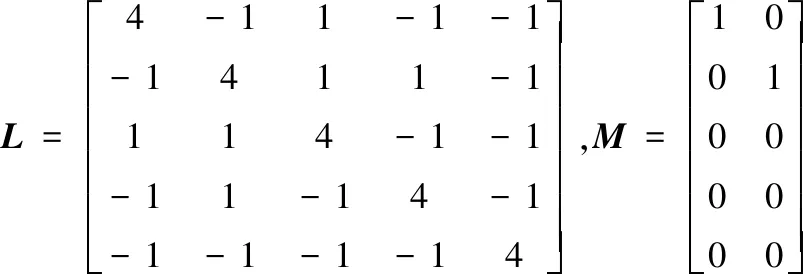
根据Tanner领航者-跟随者结构划分,系统控制矩阵和系统输入矩阵分别为:

以上结果说明,领航者-跟随者结构在对抗网络下也是适用的,并且与协作网络下系统能控性的分析有着共通性,两种网络内在的联系将在以后的文章中进行深入研究和进一步的阐述.
例2:如图3所示,网络中包含9个节点,将节点按照三部图划分为π,其中π={V1,V2,V3}.

图3 三部图划分下的9阶对抗网络
当选择红色连接边为负边,选择V2中全部节点作为领航者时,拉普拉斯矩阵和控制输入矩阵分别为:

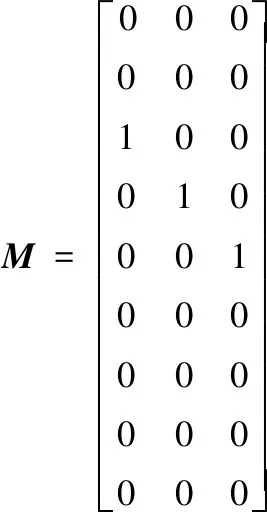
根据Tanner领航者-跟随者结构划分:

对抗网络下和对应的协作网络下的跟随者控制输入矩阵分别为:
根据卡尔曼秩判据,rank[-rFr-F2rF3r-F4rF5r]=6,rank[-rnFrn-F2rnF3rn-F4rnF5rn]=6.
这说明,定理2也适用于其他可进行三部图划分的拓扑图.
5 结 论
本文在领航者-跟随者结构的基础上,研究了对抗网络下的多智能体系统的能控性.本文将对抗作用引入到领航者-跟随者拓扑结构中,对比协作网络下的研究得出了对抗网络下多智能体系统能控的两个必要条件.此外,基于三部图划分下的Peterson图,研究得出了关于负边和领航者选择的两个条件下,对抗网络与对应的协作网络下能控性的等价性,并在推导过程中给出了定量分析.之后的工作将在此基础上对对抗网络下的简单图,例如路图、星图以及环图等,进行能控性分析.
