基于模型预测控制的远洋海岛交通船舶充电调度方案

张晋源 林湘宁 张哲原

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002； 2.华中科技大学 强电磁工程与新技术国家重点实验室，武汉 430074)

在陆地资源开发过度导致能源储备紧张的大前提下，开发利用海洋资源逐渐成为了世界各国的共同目标[1-5]．受限于技术及经济条件，目前远洋海岛仍主要依靠柴油发电．对远洋海岛而言，由于柴油等常规能源补给困难导致价格昂贵，在远洋海岛清洁能源开发实现规模开发前，船舶运营商可考虑自建小型风力发电机，在风况良好时用于给船舶充电，以降低其运营成本．若单纯利用风电进行充电，因风电出力具有随机性和波动性，和充电需求又不一定形成很好的匹配，不能保证其在出行时间到达时完成充电，因此配备常规柴机充电桩，在风电不能完全满足充电需求时进行辅助供能．

关于如何利用可再生能源发电和常规能源的协同对电动船舶进行充电的研究，国内外文献几近空白．但是，如何利用可再生能源发电和常规能源的协同对电动运载工具、如电动汽车进行充电，则已经积累了较为丰富的研究成果．其中，文献[6]提出了一种通过控制规模化电动汽车的充放电，使其能够与现有的风力/火力发电系统协同运行的优化调度策略．文献[7]介绍了近年来充电负荷、充电控制领域内的研究成果，涉及充电负荷仿真分析模型、充电控制效益、充电控制策略研究等方面，同时指出了尚未解决的问题和可能的研究方向．文献[8]在电动汽车充电与风电协同调度模型的基础上，提出了协同调度碳减排效益的测算模型，定量分析了电动汽车充电与风电协同调度在电网和交通领域的碳减排效益．

以上工作为利用可再生能源发电和常规能源的协同对电动运载工具进行充电奠定了一定的基础，但这类研究中，常规能源往往是大电网，其电价与可再生能源价格之间差异不大，因此，可再生能源提供的电能往往仅作为补充；所研究的电动汽车对象其出行时间没有刚性约束，因此，其充电策略往往仅仅是倾向于成本最低，这类对象跟本文拟研究的通勤电动船舶有显著差异，因此完全满足本文探讨的远洋海岛电动通勤船舶低成本运行策略仍属全新的领域，亟待提出新的解决方案．为此，本文拟提出一种可行的远洋海岛交通船舶充电调度方案，在对船舶蓄电池剩余电量进行监测的前提下，应用模型控制预测[9]对风电功率进行预测，并针对24 h运行于固定航线的班船[10]，研究了其充电调度方案，使得其充电成本最低．算例仿真结果验证了本文所提充电方案的有效性．

1 调度场景及基本模块简介

1.1 场景及相关参数设定

在本文场景设定中，假定某中小型远洋海岛群共有6艘通勤电动船舶，每艘船舶的电池额定功率及容量均相同．风电发电机组和柴机组额定功率需根据船舶充电的实际需求进行确定．

假定船舶航线固定，航行一圈用时5 h，耗电量为电池容量的50%，船舶的荷电状态不能低于30%，所以船舶的出行条件为：第一艘船舶出行时间为7：00am，船舶发船间隔时间为1h，刚好可以保证24 h不间断运行．船舶出行时间详见表1．

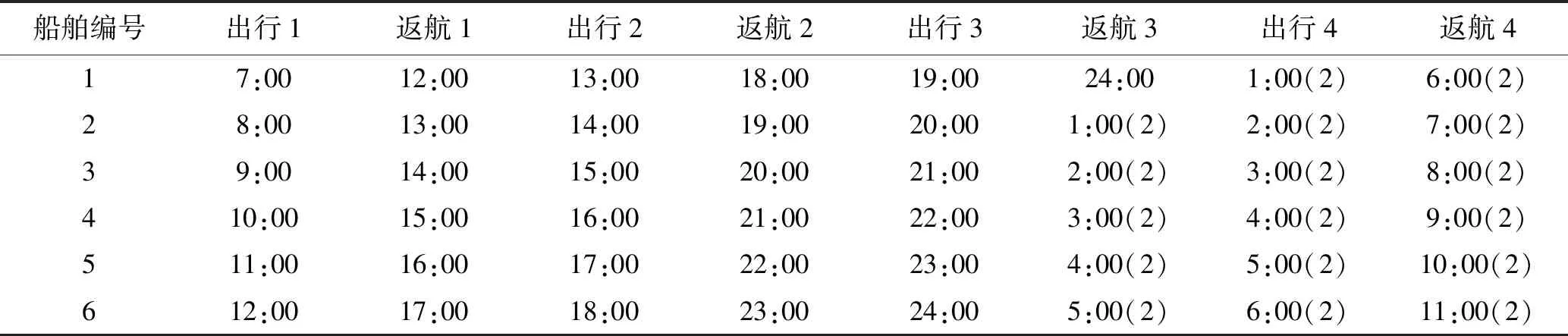
表1 船舶出行时间表

船舶运营商为了节省成本，自己利用风能发电，所发风电多余部分以1元/(kW·h)卖给电网，常规机组所发电的购买价格为5元/(kW·h)；为缩减成本，船舶的运行能源主要依靠运营商自己所发风能．由于港口空间有限，每种能源接口每次仅能对一艘船舶进行充电．

船舶电池剩余电量为EB(t)，电池容量为EBM，船舶航行一圈能量消耗固定为EC，蓄电池的荷电状态(state of charge，SOC)记为：

(1)

在第t小时内，风电发电功率为PW(t)，风电发电量为W(t)，船舶充风电量为wc(t)，柴机组发电量等于为F(t)，船舶的总充电量为S(t)，风电并网的电量为e(t)，充电成本为c(t)．

1.2 风电功率预测模块

由于超短期风电功率预测模块输出的预测结果是混合充电系统模型预测控制策略的前置输入，因此需要结合一种良好的风功率预测算法．获取同一风电场的实际功率数据，利用文献[11-14]的4种风功率预测算法对风电功率进行时间分辨率[15]为15 min、为期3 h的风功率预测，并将预测结果进行归一化评判．评判结果证明基于本文所采用的风电场功率数据，极限学习机(extreme learning machine，ELM)略优于其他算法．因此，选择采用预测前瞻周期3 h并随时间推进而实时更新的ELM算法[13]作为风电功率预测方法．

1.3 混合充电控制模块

混合充电控制模块的核心是MPC控制模块，其输入包括实时获取的最新超短期风电功率预测数据Pw(Δti)、船舶的剩余电量EB(t)以及柴机组输出功率Pf，在线求解有限时域优化问题后，输出本调度周期内的混合储能系统充放电功率．

由1.2节，风电预测信息每15 min更新一次，因此，为了在每一次迭代计算中都能恰好获取最新的预测数据，将MPC的采样时刻设置为15 min，4次采样间隔之间执行一次充电调度．

2 混合充电系统模型预测控制策略

由1.2已知，对风电功率预测的时间分辨率为15 min范围3 h．而每艘船的充电时间为1 h，所以船舶的充电时间可分为4个15 min的时段：Δt0、Δt1、Δt2、Δt3，再将此4段分为两段，前45 min为时段A，最后15 min为时段B，则A、B段的风电发电量分别为WA、WB：

WA(t)=Pw(Δt0)×Δt+

Pw(Δt1)×Δt+Pw(Δt2)×Δt

(2)

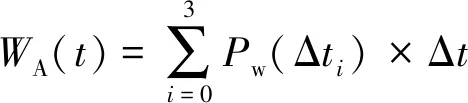
(3)

WB(t)=Pw(Δt3)×Δt

(4)

设在第t小时，船舶充电前后的剩余电量分别为EBq(t)和EBh(t)．充电系统的调度策略与船舶充电前剩余电量EBq(t)和充电时间内的风电功率Pw(t)有关．

常规机组将电池SOC由30%提升至80%用时设定为

(5)

针对此情况，制定了如下调度策略：

①船舶起充前的剩余电量与预测的风电发电功率足够大时，即在1 h内仅用风电便可将船舶的剩余电量充满．即满足公式：

(6)

则调度策略1为：对船舶充风电至满后将风电并网．在此情景下，船舶充风电量为

wc(t)=EBM-EBq(t)

(7)

柴机组发电量F(t)为零；船舶的总充电量为

S(t)=wc(t)

(8)

风电并网的电量为

e(t)=EB(t)+W(t)-EBM

(9)

充电成本为

c(t)=-1×e(t)

(10)

②当船舶起充前的剩余电量与预测的风电发电功率满足公式：

Pw(Δt3)×Δt≤EBM

(11)

即在1 h内风电量满足出行条件但不能使电池充满，则需要在第45 min的预测考虑20%的偏差裕度，当满足公式：

0.8×Pw(Δt3)×Δt

(12)

即最后15 min预测风电量的80%与船舶起充剩余电量及前45 min充电量之和达到0.8EBM．

调度策略2为：继续对船舶充风电最后15 min在此情景下，船舶充风电量为

wc(t)=W(t)

(13)

柴机组发电量为零；船舶的总充电量为

S(t)=wc(t)

(14)

风电并网的电量e(t)为零；充电成本c(t)为零．

③若不能满足方程(12)，则调度策略3为：对船舶充45 min风电后，切换到常规机组充电至满足出行条件为止，风电在45 min时并网直到下一艘船接入充电．在此情景下，船舶充风电量为

wc(t)=WA(t)

(15)

柴机组发电量为

F(t)=0.8EBM-EB(t)-WA(t)

(16)

船舶的总充电量为

S(t)=wc(t)+F(t)

(17)

风电并网电量为

e(t)=WB(t)

(18)

充电成本为

c(t)=-e(t)+5×F(t)

(19)

④若船舶起充前的剩余电量与预测的风电发电功率过小，既不满足公式(6)也不满足公式(11)，此时：

(20)

即风电充1 h不考虑20%的偏差裕度也无法满足出行条件，则执行的调度策略4与调度策略3相同．在此情景下，船舶充风电量为

wc(t)=WA(t)

(21)

柴机组发电量

F(t)=0.8EBM-EB(t)-WA(t)

(22)

船舶的总充电量为

S(t)=wc(t)+F(t)

(23)

风电并网电量为

e(t)=WB(t)

(24)

充电成本为

e(t)=-e(t)+5×F(t)

(25)

在1 h的充电调度中，最后15 min的充电策略是核心．需根据考虑了偏差裕度的最后15 min的风电预测发电量大小，进行充电策略的调整．若公式(12)满足，则最后15 min不用切换电源，否则必须切换．

MPC充电策略执行流程图如图1所示．

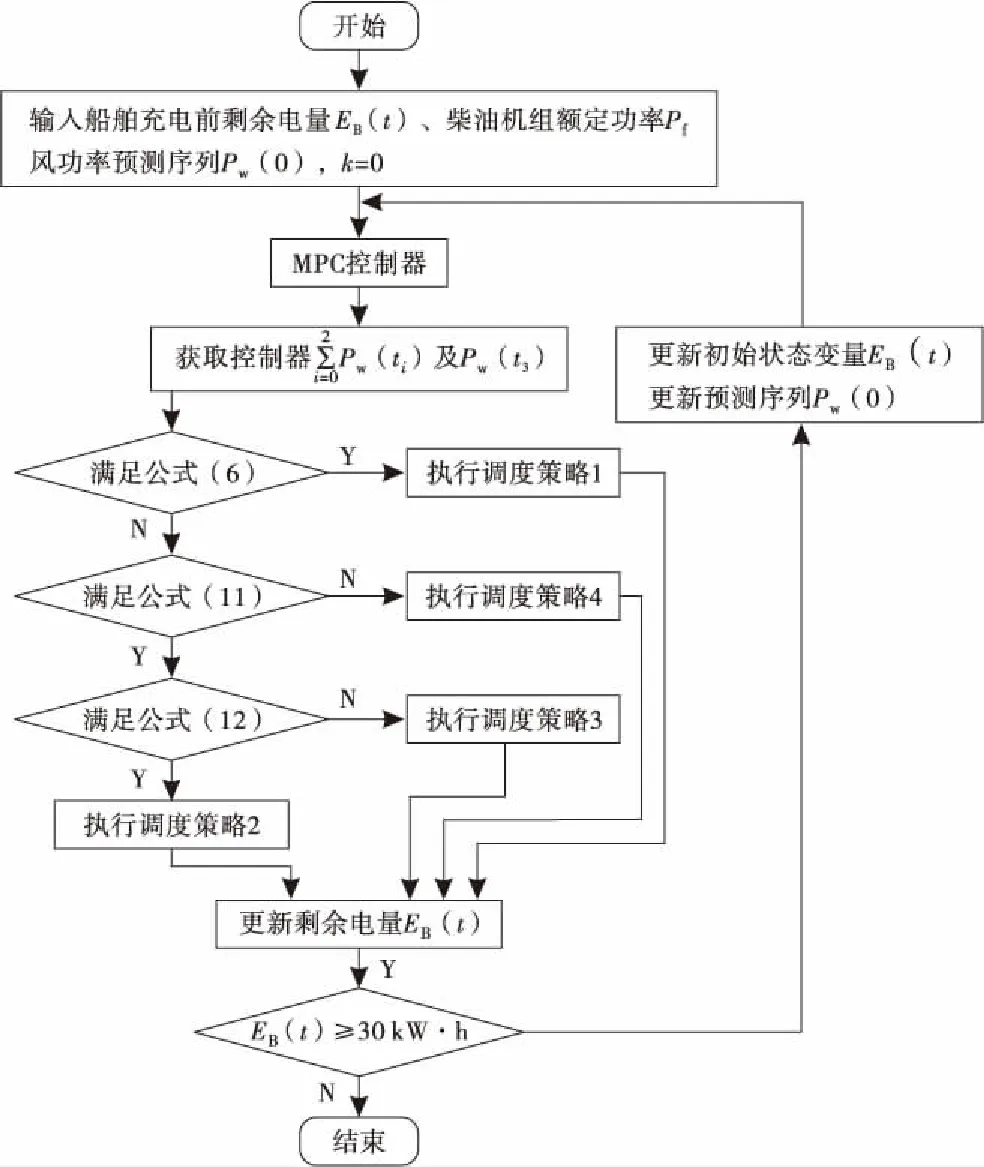
图1 模型预测控制充电策略执行流程

3 算例分析

3.1 算例场景

算例共有6艘通勤电动船舶，每艘船舶的电池额定功率均为200 kW，容量均为100 (kW·h)．风电发电机组及柴机组最大功率为200 kW，船舶航线固定，航行一圈用时5 h，耗电量为50 (kW·h)，船舶的荷电状态不能低于30%，出行时荷电状态不能低于80%．仿真在Matlab平台中进行．

风电发电机组和柴机组额定功率需根据满足船舶出行的充电需求进行确定．一般而言，船舶蓄电池的荷电状态SOC必须始终≥30%，否则会损害电池寿命．在上面已假定电池容量为100 (kW·h)，船舶航行一周耗电量为50 (kW·h)，因此船舶出行时蓄电池的荷电状态约束必须SOC≥80%．由于对于实时调度和超短期预测而言，其调度周期和预测周期均为15 min，最不利的情形是：在实时调度的最后一个周期(15 min)到来前，由于无风，电池SOC总维持30%，且预测发现最后15 min仍无风，为满足出行需要，在充电的最后15 min由常规电源充电至80%，即充入50 (kW·h)的电量，由此折算得到的柴机组功率应为200 kW．

至于风机的定容，在最理想的风况下(额定风速～25 m/s)，风机能按额定功率输出，则其容量定为50 kW完全可以在1h充入50 (kW·h)的电能，满足船舶出行的需要．但实际风速在很多时候低于额定风速，为尽可能利用风能，风机功率应该适当提高，当其功率提高至200 kW时，一方面，该功率适配了电池功率，另一方面，即便前45 min仍无风，一旦最后15 min风速在额定风速以上，仍可以仅由风机充电至80%，满足船舶出行需求．如继续提升至200 kW以上，当风速达额定风速以上后，风机输出功率已经超过电池额定功率，如不想弃风，必须再配置一台与电网连接的逆变器，这变相增加了投资和运行成本，显然是不太恰当的．因此，风机的适当功率应在50 ～200 kW之间．为充分利用风能，本文姑且建议风机定容按上限，即也定为200 kW．在工程中具体该如何定容，应根据实际风况、以及海岛电网收购风电的价格等确定．

关于建模时的风电出力数据来源，从文献[16]获取了某风电场全年8 760 h的风速数据，由于该数据是以1 h为分辨率，超短期预测需用到15 min为分辨率的数据，远洋海岛上的以15 min为分辨率的风速数据不论从文献还是从现场调研都不易获取．为此，对上面的风速数据进行了内插，形成了8 760×4个基础数据，再从中截取了48 h的数据作为典型日数据，如图2中的红色曲线所示，横坐标每15 min为一刻度，也代表了调度的分辨率．在此基础上，运用1.2节描述的ELM算法进行超短期预测，得到风电超短期预测的时间序列，如图2中的蓝色曲线所示．调度方案生成依据的正是以上超短期预测数据．

图2 典型日风电功率输出及其预测波形(每0.25 h)

3.2 典型日充电调度效果对比

3.2.1 典型日柴机单独作用下充电效果

由于默认船舶首次出行前电池电量为满状态，所以第一艘船实际开始充电时间为12：00，所以相应调度数据从12：00开始采集．

当只有柴机作用时，典型日柴机发电量如图3所示，当经过前12 h消耗后，6艘船从18：00开始，航行一圈消耗的50 kW·h电能均由常规机组补充．

在柴机单独作用下，充电成本均源于购置柴机发出的电能，该成本与充电所消耗的总电量成正比，每个小时的充电如图4所示，经积分计算后得到充电总成本，为5 150元．

3.2.2 典型日风机柴机共同作用下充电效果

图5所示为风电(蓝色)与柴机电(红色)之和在典型日各小时段发电量波动图．16-19、34-36、41、42为第2节中情景①的调度；22、25、28、37、40、45显示了情景②的调度；由第2节可知，情景③与情景④的调度方式相同，所以剩余部分皆为情景③、④的调度方式．

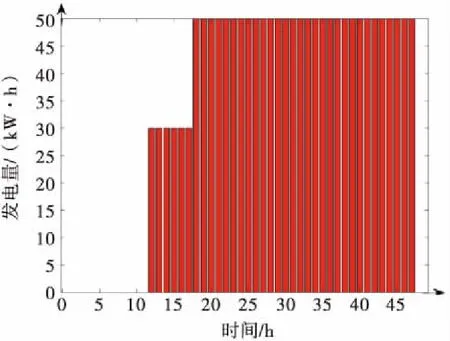
图3 柴机单独作用下典型日发电量

图4 柴机单独作用下典型日充电成本

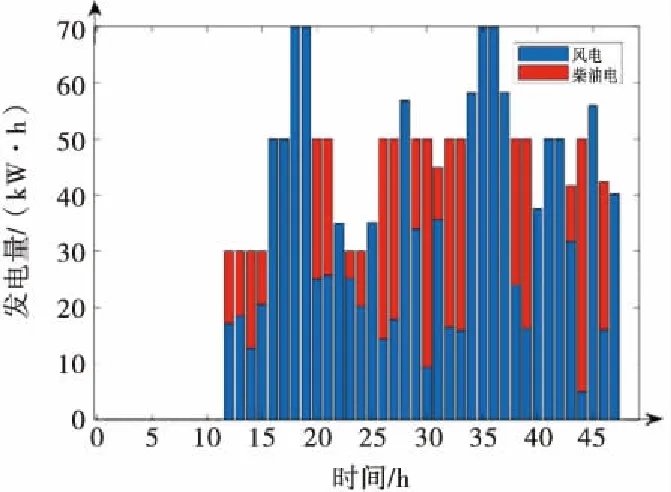
图5 典型日风力发电机及柴机发电量累计时序序列

风电并网电量如图6所示，出现第2节中情景②时，并网风电量为零．

图6 典型日每小时并网风电量波动图

对由柴油发电机和风机互为补充充电的模式而言，典型日的充电成本曲线如图7所示．其中，由柴油机充电的那部分电量其成本与充电所消耗的总电量成正比，以5元/(kW·h)产生正的成本，由风电充电的那部分电量则成本为零；当充风机单独出力已经能正好满足船舶充电需求时，充电的运行成本为零；当充风机单独出力不仅能满足船舶充电需求还有富余，该富余电能向电网回馈，可以收到1元/(kW·h)卖电利润，导致充电的运行成本为负，如图8的横轴下半部分波形所示，这正好验证了情景①仅有风电发电且风电有余量的情况；而充电成本为零则验证了情景②风电量能满足出行条件但不够电池充满的情况．对图7的波形进行积分计算，得到其充电总成本为2 241.3元，相对于单纯柴机发电，成本降低了56.47%．

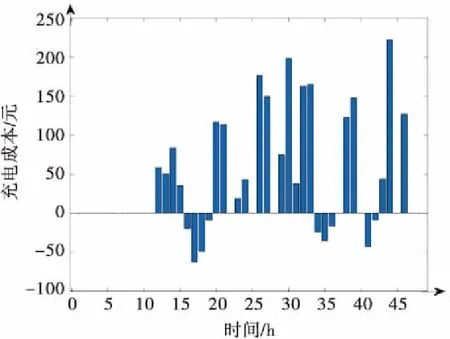
图7 典型日每小时发充电成本

典型日各小时船舶出发前SOC状况如图8所示．在情景①的调度策略执行后，船舶电量充满；情景②的调度策略执行后，船舶虽不能充满，但SOC超过出行条件要求的80%；而情景③和情景④对应的调度策略刚好使得船舶在出行前SOC达到80%．

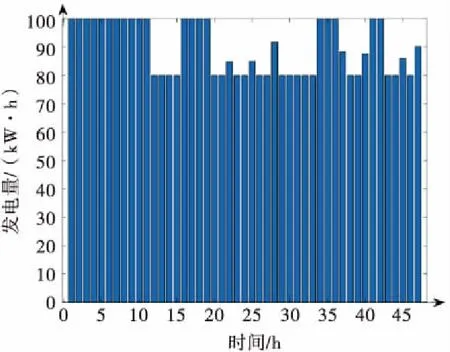
图8 典型日各小时船舶出发前SOC波动图

4 结 语

本文提出由风电发电桩和常规柴机组发电桩组成的充电系统，设计出通过输入船舶充电前剩余电量并根据风电功率的预测结果，采用MPC方法求取最优充电调度决策．算例仿真表明，该方案能充分利用MPC控制方法的前瞻性优势，实现对船舶充电的优化调度，完成减小充电成本的目的．