界面过渡区力学特性对水工混凝土断裂性能的影响

金永苗 徐 磊 陈在铁 周昌巧 王绍洲

(1.河海大学 水利水电学院，南京 210098; 2.沙洲职业工学院，江苏 张家港 215600)

目前，在细观层次上混凝土一般被视为三相复合材料，即由砂浆、骨料和界面过渡区(Interface Transition Zone, ITZ)构成．ITZ位于骨料与砂浆之间，具有抗拉强度低、弹性模量低和高渗透性等特点，是混凝土中的薄弱面[1-4]．K.M.Lee利用数值模拟验证了ITZ的存在会降低混凝土的宏观弹性模量[5]．朱万成等根据强弱骨料的对比证实了ITZ的存在会对混凝土断裂模式产生影响[6]．于庆磊等利用数字图像技术建立有限元模型探究了ITZ抗拉强度对于混凝土抗拉强度及断裂模式的影响[7]．

一般而言，材料的力学参数应通过力学试验获取，但由于ITZ是两种材料之间厚度较薄的界面过渡区，通过试验手段直接获得其力学参数极为困难．近年来已有学者对ITZ的微观结构以及化学成分开展研究[4]，但仍未实现其力学性能的测定．因此，在混凝土细观力学分析中，通常采用人为假定的方法确定ITZ的力学参数，存在很大程度的主观任意性．此外，研究表明混凝土材料的断裂一般首先出现在ITZ中，进而扩展至砂浆，最终形成裂缝[8]．故此在混凝土细观分析中，ITZ力学参数选取的合理性与否在很大程度上决定分析结果的合理性．

本文通过建立全级配混凝土细观有限元计算模型，并假定不同的ITZ参数取值，分析了不同ITZ力学参数的取值下，全级配混凝土宏观断裂性能，系统研究了界面过渡区力学特性对水工混凝土断裂性能的影响规律，研究成果可为水工混凝土细观数值模拟中ITZ力学参数的取值提供参考．

1 混凝土细观有限元计算模型

采用细观有限元分析方法研究ITZ力学参数对水工混凝土宏观断裂性能的影响，首先需依据水工混凝土骨料含量和级配，生成混凝土细观随机结构，进而对其进行网格划分，并对骨料、砂浆和ITZ的力学特性进行模拟，最后开展计算分析．

1.1 细观结构生成

本文以水工全级配混凝土作为研究对象，骨料平面含量取为50%，骨料级配取为小骨料∶中骨料∶大骨料∶特大骨料=25∶25∶20∶30．尺寸小于5 mm的细骨料被视为砂浆，并将砂浆看作是均匀连续介质．本文采用“take-and-place”参数化建模方法生成混凝土细观结构，基本步骤如下：①确定骨料投放区域；②确定骨料中心点位置，并生成多边形骨料；③判断骨料位置是否符合要求，若不符合，则重复步骤②；④判断骨料含量是否满足要求，若不满足，则继续投放骨料．所生成的细观结构如图1所示．

图1 细观结构

1.2 网格划分

在生成混凝土的细观结构后，为了能够实现对结构自动划分网格，本文基于MATLAB和PYTHON混合编程自动调用ABAQUS的前处理模块对骨料和砂浆进行网格剖分．网格剖分流程如下：①将细观结构的几何信息导入ABAQUS；②指定网格离散参数，并调用ABAQUS的前处理模块对导入的几何结构进行网格剖分．但由于ITZ厚度仅有100 μm[9]，难以直接对其进行网格剖分，故此时所生的网格并未包含ITZ．为此，通过自行编制的程序在砂浆与骨料之间自动插入的界面单元以模拟ITZ．有限元网格如图2所示．

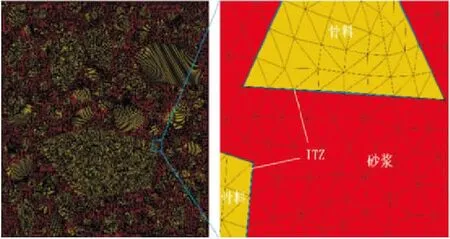
图2 有限元网格

1.3 细观本构模型与力学参数

研究表明，混凝土断裂通常肇始于ITZ中，随后扩展并延伸至砂浆基质中，直至形成宏观裂缝，在这一过程中，骨料一般不会发生破裂[10]．因此，本文采用线弹性本构模拟粗骨料，采用塑性损伤模型(CDP)描述砂浆与ITZ的力学行为．

d=1-(1-Stdc)(1-Scdt)

(1)

其中，St和Sc是应力状态函数，用于描述刚度恢复的影响．损伤弹性模量E:

E=(1-d)E0

(2)

(3)

其中，σ是柯西应力．CDP模型中屈服函数为:

(4)

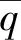
(5)

为了合理的考虑剪胀性，在CDP模型中采用了非关联流动法则，塑性势函数G:

(6)

1.4 加载方式与数值求解方法

由于具有不同细观结构的随机混凝土试件，其断裂特性也存在差异[2,11-12]．为排除骨料形状以及分布对实验结果的影响，本文针对同骨料形状及分布的数值试件进行拉伸断裂模拟．为真实模拟混凝土的断裂性能，本文采用异步粒子群优化算法[13]对砂浆的主要细观力学参数(弹性模量、抗拉强度以及断裂能)进行标定，标定目标为《混凝土结构设计规范》GB 50010-2002中C20混凝土的单轴拉伸理论曲线．表1给出了砂浆与骨料的主要力学参数．

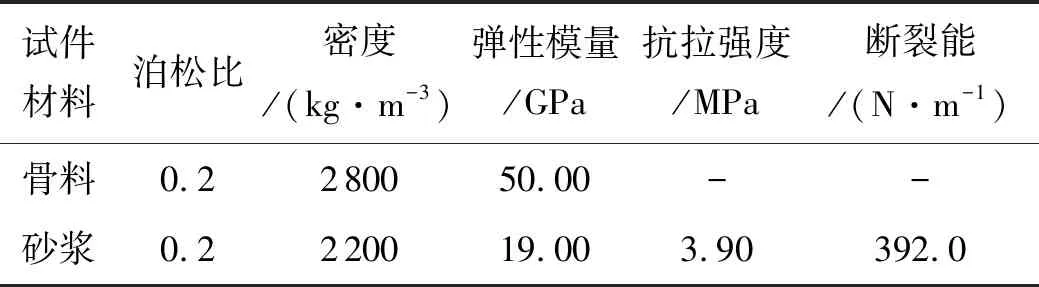
表1 砂浆与骨料力学参数表

考虑到混凝土断裂是一个典型的准脆性断裂过程，通常伴有明显的软化阶段，故采用常规的隐式求解方法一般会出现不收敛问题，难以获取较为完整的拉伸应力-位移曲线，故本文采用显示动力学求解方法进行混凝土单轴拉伸模拟．通过对本文的数值试件进行大量试算，最终确定加载速率为5 mm/s，在此加载速率下，模型的惯性效应很小，符合准静态加载的特征．与物理试验保持一致，水工全级配混凝土细观模型尺寸取为450 mm×450 mm，模拟中采用位移加载方式，即模型左侧边界约束法向位移，模型右侧边界施加均布位移，加载位移取值为0.000 27 m(即相当于600个微应变)．

2 影响分析

为研究ITZ力学特性对水工混凝土断裂性能的影响，本文开展了一系列单轴拉伸数值模拟．为体现ITZ的软化特性，假定ITZ力学参数为砂浆力学参数的0.9倍，并进行单轴拉伸数值模拟．在此基础上，分别逐级降低ITZ的弹性模量、抗拉强度与断裂能，并开展相应的数值分析以单独研究上述参数的取值对混凝土宏观断裂性能的影响．

2.1 ITZ弹性模量对混凝土断裂性能的影响

为研究ITZ弹性模量对水工混凝土断裂性能的影响，将ITZ弹性模量逐级降低为砂浆弹性模量的0.8，0.7，0.6和0.5倍，二者的比值用R(E)表示．图3(a)给出了R(E)不同量值时的宏观应力-位移曲线，与之相应的断裂模式以及主要宏观力学指标(弹性模量、抗拉强度、峰值应变以及断裂能)见图4和表2．

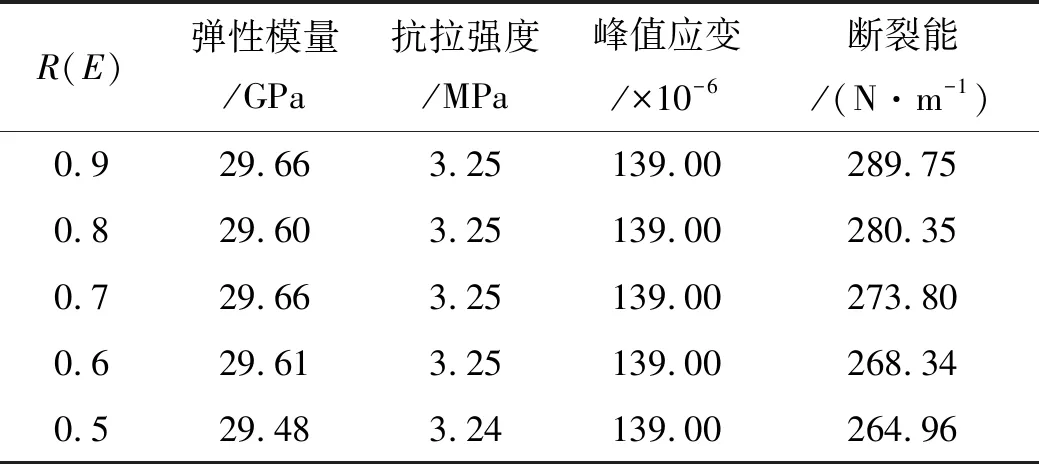
表2 ITZ弹性模量对水工混凝土断裂性能的影响

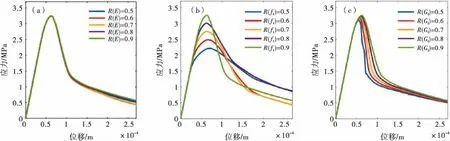
图3 宏观应力-位移曲线

图4 断裂模式

从图3(a)中可以看出，在不同的比值下，各宏观应力-位移曲线均体现了混凝土典型的准脆性拉伸断裂软化过程．从表2中可知，随着ITZ弹性模量取值的逐渐降低，水工混凝土各宏观力学性能指标基本无变化．从图4中可以看出，混凝土断裂模式基本未发生变化．以上表明ITZ弹性模量对水工混凝土断裂性能的影响很小．

上述结果的主要原因在于ITZ弹性模量主要对混凝土的弹性行为有影响，但由于其所占体积很小，导致ITZ弹性模量对混凝土的断裂性能影响很小．

2.2 ITZ抗拉强度对混凝土断裂性能的影响

通过逐级降低ITZ抗拉强度以研究ITZ抗拉强度对水工混凝土宏观断裂性能的影响．ITZ抗拉强度与砂浆抗拉强度的比值R(ft)分别取为0.8、0.7、0.6和0.5．不同R(ft)取值时水工混凝土的宏观应力-位移曲线及其断裂模式分别如图3(b)和图5所示，与之相对应的主要宏观力学指标见表3．

表3 ITZ抗拉强度对水工混凝土断裂性能的影响

图5 断裂模式

由图3(b)可以看出，ITZ的抗拉强度对混凝土宏观力学性能影响较为显著．这主要体现在随着R(ft)的变化，混凝土的宏观应力-位移曲线出现较为明显的改变．从表3中可知，随着R(ft)由0.9降低至0.5，峰值应变逐渐增加，混凝土的抗拉强度呈现降低趋势，而弹性模量变化很小，这与图3(b)所示的宏观应力-位移曲线相一致．从图5和表3中可以看出，ITZ抗拉强度对水工混凝土的断裂模式有着明显的影响，相应的断裂能也因此发生改变．

出现上述现象的主要原因在于ITZ抗拉强度降低，使得其更容易破坏进而导致试件的断裂．混凝土的断裂模式不同，导致其断裂能也不相同，当断裂路径较长时，所耗散的断裂能较大．总体而言，ITZ的抗拉强度对水工混凝土断裂性能有很大影响．

2.3 ITZ断裂能对混凝土断裂性能的影响

为了研究ITZ断裂能对水工混凝土断裂性能的影响，ITZ断裂能逐级降低为砂浆断裂能的0.8、0.7、0.6和0.5倍，并用R(Gf)表示ITZ断裂能与砂浆断裂能的比值．图3(c)和图6分别给出了R(Gf)取不同量值时水工混凝土的宏观应力位移曲线及其断裂模式，相应的混凝土宏观断裂性能指标列于表4．

表4 ITZ断裂能对水工混凝土断裂性能的影响

图6 断裂模式

结合图3(c)和表4可以看出，随着ITZ断裂能的降低，混凝土的抗拉强度与峰值应变也随之减小，但混凝土的弹性模量基本未发生改变．从图6和表4中可以看出，ITZ断裂能的变化对混凝土断裂模式基本未产生影响，但随着ITZ断裂能降低，混凝土断裂能逐渐减小．

综上可知，ITZ断裂能对水工混凝土断裂性能的影响主要体现在对混凝土断裂能的影响，其主要原因在于混凝土的裂缝主要形成于ITZ和砂浆中，而ITZ断裂能的降低使得在混凝土中形成裂缝所耗散的能量减少．

3 结 论

为研究ITZ的力学特性对水工混凝土断裂性能的影响，本文建立了水工全级配混凝土细观有限元计算模型，并通过对ITZ的弹性模量、抗拉强度和断裂能分别逐级降低，单独分析上述参数对水工混凝土断裂性能的影响，主要结论如下：

1)ITZ弹性模量对水工混凝土断裂性能影响很小．

2)随着ITZ抗拉强度降低，水工混凝土的抗拉强度减小，峰值应变逐渐增加，断裂模式也呈现出明显变化，并导致断裂能的改变，但弹性模量变化很小．

3)ITZ断裂能对水工混凝土断裂性能的影响主要体现在混凝土断裂能上，而抗拉强度、峰值应变、弹性模量以及断裂模式受其影响较小．

需要说明的是，本文结论仅适用于在特定条件下的水工四级配混凝土．