基于虚拟磁链预测直接功率控制的双PWM变频调速系统研究

王 辉 李宇豪 张文博 李静怡 赵冬阳

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.三峡大学 湖北省微电网工程技术研究中心，湖北 宜昌 443002)

双PWM变频调速系统的动、静态性能要求越来越高，因此对其控制策略的提出有了更高的要求[1]．

针对双PWM变频调速系统的整流侧，目前实际应用较多的控制策略是直接电流控制．文献[2]采用基于空间矢量脉宽调制(SVPWM)的直接电流控制．该方法采用解耦电流双PI闭环控制策略，其动态性能较好，但PI控制器参数设计相对复杂．文献[3]采用传统直接功率控制(Direct Power Control，DPC)电压外环采用PI控制，功率内环采用滞环比较器，通过查询开关矢量表来选择开关电压矢量．该方法无需坐标变换，算法、结构简单．但开关频率不固定，同时造成无功失控．文献[4]通过分析开关电压矢量对瞬时功率的调节作用，提出一种18扇区矢量空间划分方法，提高系统动静态性能．文献[5]结合虚拟磁链(Virtual Flux，VF)控制算法，通过取消网侧电压传感器，从而实现控制电路与主电路的隔离，提高电路可靠性，简化电路结构、降低了硬件设计成本．文献[6]提出了一种模型预测直接功率控制(Model Predictive Direct Power Control，MPDPC)，通过性能优化目标函数来选择最佳控制电压矢量，但其未考虑采样延迟问题．文献[7]介绍了一种基于模型预测原理的直接功率优化控制策略，未考虑稳态时有功、无功误差为零问题．

为解决上述问题，本文建立了整流侧在两相静止坐标系下的数学模型．整流侧在瞬时有功和无功功率原理的基础上，结合模型预测控制理论提出一种基于虚拟磁链定向的模型预测直接功率控制策略．该控制算法内环采用虚拟磁链模型预测直接功率控制模块，无需经电压传感器来测得电网电压，降低系统控制难度．通过构造有功、无功误差最小目标函数，采用两步预测法预测参考功率给定值，使控制延时所带来的误差在最大程度上被减小，且采用重复控制对系统稳态有功和无功功率误差进行修正，通过SVPWM实现MPDPC．逆变电机侧采用转子磁场定向矢量控制(Rotor Flux Orientation Control, FOC)策略．最后对该双PWM变频调速系统进行了仿真验证．

1 双PWM变频调速系统的数学模型

典型的双PWM变频调速系统的拓扑结构如图1所示．

图1 双PWM变换器拓扑结构

图1中，esa，esb，esc为三相对称交流电网电压源；isa，isb，isc为整流器网侧三相线电流；L为网侧滤波电感，R为网侧等效电阻；vsa，vsb，vsc为整流器交流侧输入相电压；C为直流侧滤波电容；udc为直流侧母线电压．

根据基尔霍夫定律在两相静止坐标系下建立电压型PWM整流器的动态方程为[8]：

(1)

图1中电机为三相异步电机，参考文献[9]已列出其数学模型．

2 双PWM变频调速系统控制策略

2.1 整流侧基于VF模型预测直接功率控制

波兰学者Mariusz Malinowski 提出基于虚拟磁链定向的直接功率控制策略．引入虚拟磁链定义，因此省去电网电压传感器，系统成本相对减小．

网侧变换器的虚拟磁链定义为[10]：

(2)

式中：Ψs=[Ψsα，Ψsβ]T，es=[esα，esβ]T．

根据瞬时功率理论：

(3)

利用VF将上式表示为：

(4)

对式(4)求导，可得：

(5)

由式(1)可知：

(6)

虚拟磁链与电网电压的关系为：

(7)

将式(6)、(7)代入式(5)，可得

(8)

假设t=k时，瞬时有功和无功的导数表达式为

(9)

式中的导数方程可以用线性一阶方程表示，故可得下一周期开始时的有功无功的预测值为：

(10)

因采用SVPWM调制技术，整流器需要获得准确的交流输出电压矢量(vsα，vsβ)，这样才能获得较好地控制效果．为了使在下一个采样周期结束时有功和无功的实际值与给定参考值误差最小，定义性能优化目标函数F．

F=[pref(k+1)-p(k+1)]2+

[qref(k+1)-q(k+1)]2

(11)

由于存在一个周期的采样延时，因此加入延时补偿，利用两步预测消除这种延迟，得到新的目标函数：

F′=[pref(k+2)-p(k+2)]2+

[qref(k+2)-q(k+2)]2

(12)

将式(10)代入式(12)得：

F′=[pref(k+2)-p(k+1)-Tδp]2+

[qref(k+2)-q(k+1)-Tδq]2

(13)

为了使目标函数最小，使式(13)对电压矢量(vsα，vsβ)的偏导数为零，得

(14)

式中：εp=pref(k+1)-p(k+1)，εq=qref(k+1)-q(k+1)．

另外，磁链和电流的预测值由泰勒级数的二阶展开式求得：

Ψα(k+1)=2Ψα(k+0.5)-Ψα(k)

(15)

2.2 重复控制

在模型预测直接功率中，功率并非连续变化，当系统处于稳态时，有pref=p(k+1)，qref=q(k+1)．则εp=0，εq=0．由式(14)知，瞬时有功和无功的误差为零后，系统不能有效地控制输出合适的电压矢量．为解决此问题，本文在虚拟磁链预测直接功率控制策略中加入重复控制的修正方法．功率误差的存在使系统在稳态时保持相应的功率变化，能达到动态平衡．

重复控制是一种基于内膜原理的控制方法，是由Inous T.在1981年提出．图2虚线部分为改进型重复信号发生器，Q(z)为滤波衰减环节，通常取小于1的常数，在此取0.95；Z-N为周期延时环节；N为采样次数．其传递函数为：

(16)

因此，输入输出信号之间的关系表达式为：

y(k)=e(k)+Q(z)y(k-N)

(17)

图2 重复信号控制器功率修正框图

每经过一次采样周期，输出量就会累加一次．即上一采样周期(k-N)Ts时刻输出量y(k-N)与Q(z)相乘之积，加上当前采样kTs时刻误差e(k)，一同作为当前采样时刻的输出．

在kTs时刻，根据上述公式，将该时刻功率预测值p(k+1)加上前k次预测误差之和，对该时刻的预测值进行修正，得到修正预测值：

(18)

同理可得：

(19)

2.3 综合控制策略

逆变侧采用矢量控制(FOC)[9]策略．根据前面分析，将整流侧与逆变侧控制策略相结合，如图3所示为双PWM变频调速系统总体控制框图．

图3 双PWM变频调速系统总体控制框图

3 仿真分析

3.1 仿真参数

为了验证本文所采用控制策略的正确性和可行性，在Matlab/Simulink中搭建双PWM变频系统仿真模型．整流侧具体仿真参数见表1，电机侧仿真所用参数见表2．

表1 整流侧参数

表2 电机侧参数

3.2 系统稳态响应

图4～8所示为三相双PWM变频调速系统采用本文所提出的控制策略后的稳态波形．从图4中可以看出，直流侧稳态电压稳定在650 V左右，图5为直流侧电压放大后波形，可以看出纹波非常小．图6为交流侧a相电压电流波形图，为方便观察，其中网侧a相电流放大4倍，两者波形同相位，且电流波形成正弦．图7为稳定有功功率和无功功率，波形很稳定，超调量小，其纹波也非常小，其无功功率的值恒为0，实现单位功率因数运行．图8为实际有功跟踪给定有功波形，有功实现无误差准确跟踪预测值．

图4 直流母线电压波形

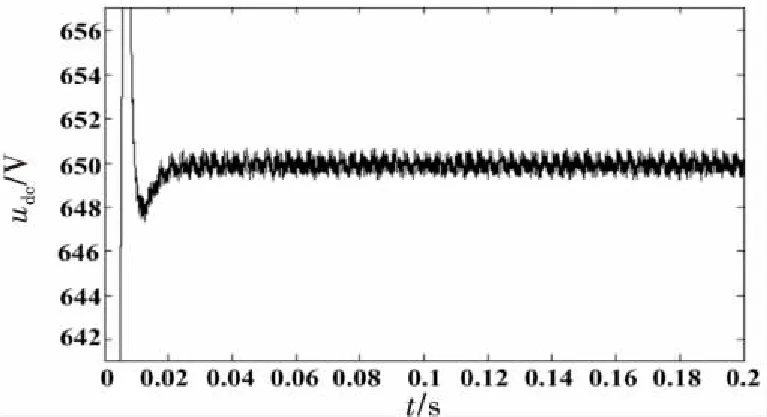
图5 直流母线电压放大波形

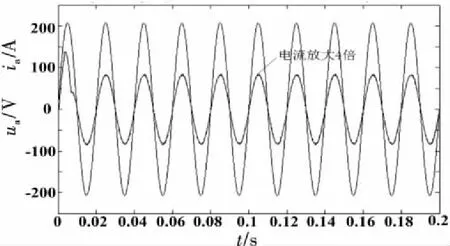
图6 a相电网电压与电流波形

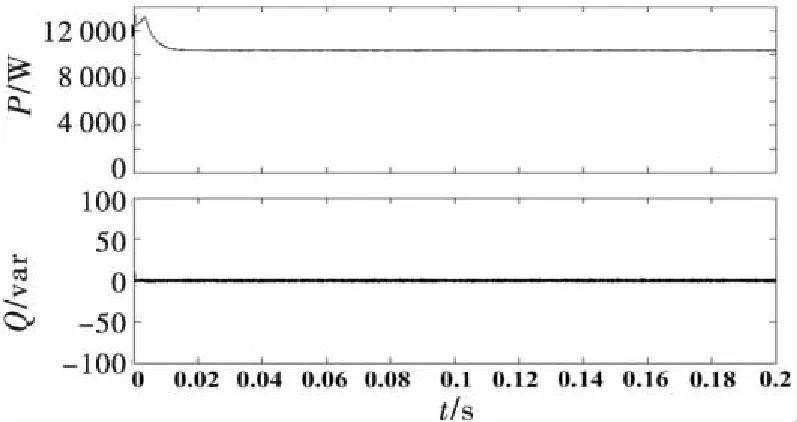
图7 网侧有功和无功波形

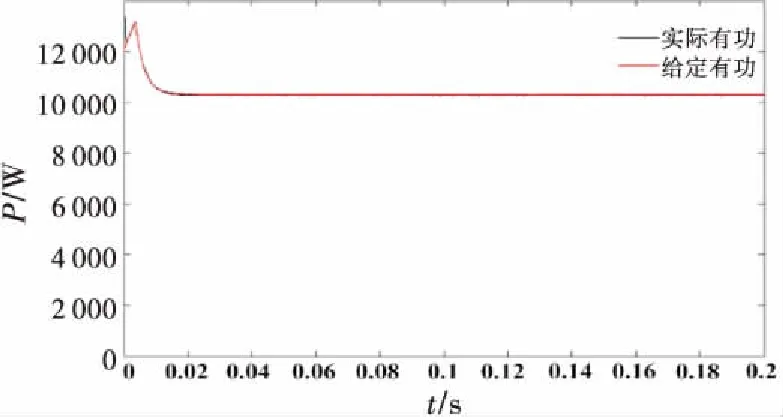
图8 有功功率跟踪波形

3.3 系统动态响应

动态响应过程：给定转速为100 rad·s-1，在0.1 s时电机转矩Te由100 N·m突变到120 N·m．图9～12分别为直流侧电压、直流侧电压放大、网侧a相电压电流波形、网侧整流器的有功功率波形图，为方便观察，其中网侧a相电流放大4倍．

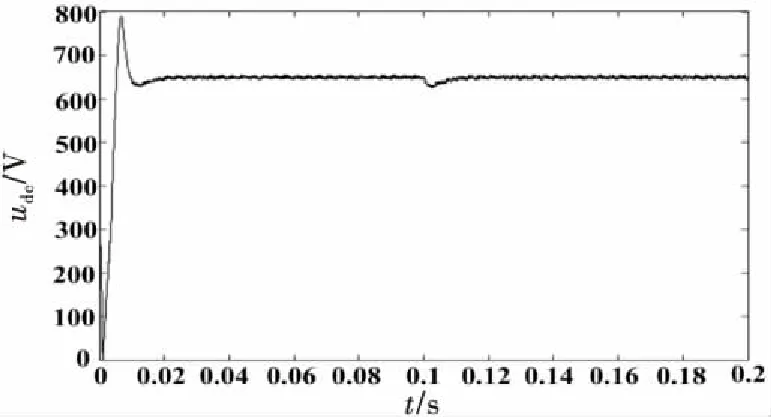
图9 直流侧电压波形

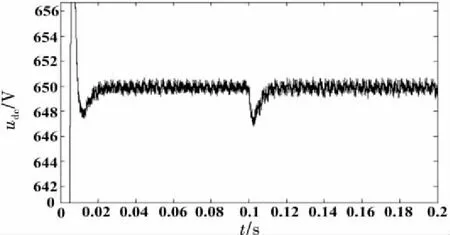
图10 直流侧电压放大波形

图11 网侧a相电压和电流波形

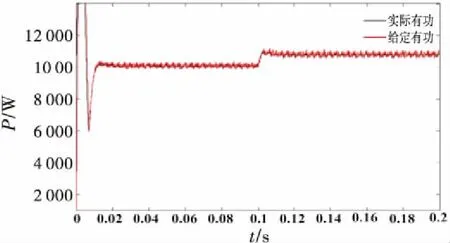
图12 整流侧有功功率波形

从仿真结果可以看出在网侧采用虚拟磁链模型预测直接功率控制，并引入两步预测和重复控制，在负载突变的情况下，直流电压经过较小波动且经过0.005 s重新达到稳态，电压波动不到4 V，系统抗扰性能好．网侧电压电流动态恢复快，网侧电压和电流相位仍保持同步．在突加负载时，有功功率始终与预测值保持一致，且动态响应速度较快．表明双PWM变换器在单位功率因数状态下运行．

图13为a相电网电流傅里叶分析结果图，其中横坐标表示的是谐波次数，纵坐标表示谐波含量．其总电流谐波畸变率(total harmonic distortion，THD)为2.13%．从其傅里叶分析结果可知，并且依据谐波电流相关标准，通常认为THD≤5%范围内是允许的．

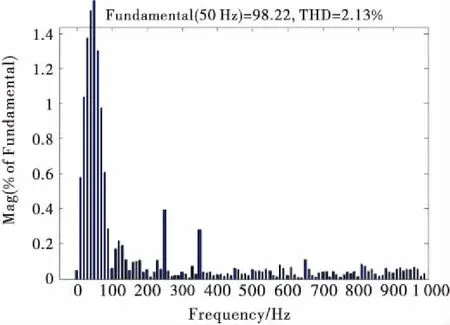
图13 电网电流傅里叶分析

4 结 语

本文针对双PWM变频调速系统提出一种控制策略．电网整流侧采用VF-MDPC策略，即一种基于虚拟磁链的模型预测直接功率控制策略．该控制策略采用两相静止坐标系减小运算量，并且借助两步预测和重复控制优化控制系统性能．逆变电机侧采用转子磁链定向矢量控制(FOC)策略，提高电机调速性能．VF-MDPC策略与FOC策略二者相互结合，不需增加协调控制策略，简化双PWM变频系统控制器结构．仿真结果表明，该控制系统具有较好稳态特性，并且动态响应速度快，直流侧电压纹波小，三相输入电流谐波畸变率小，抗干扰性能强．