基于盒粒子滤波的多扩展目标伯努利滤波算法

赵小龙

(安徽工业经济职业技术学院计算机与艺术学院，安徽 合肥 230051)

0 引言

多目标跟踪是指通过对传感器得到的量测数据进行处理，以实现对目标个数和状态的持续估计。作为一项关键技术，在诸如机器人、监控、自动驾驶、自动化和传感器网络中都有着广泛的应用。

传统的目标跟踪均采用点目标模型，并且在大量的实际应用场景中，这种假设也是合理的。然而由于传感器技术在近年来的快速发展，目标占据着越来越多的分辨单元，如在移动机器人和自动驾驶中，点目标的假设便难以适用。对此，我们将占据多个传感器分辨单元的目标称为扩展目标[1-2]，这类跟踪问题便称为扩展目标跟踪(EOT，Extended Object Tracking)。扩展目标具有不同空间分布的多个量测源，也称作反射点，这些点会产生多个测量值。如何更好地对目标进行位置估计，需要建立当前目标和其测量值得关联，当目标数较多时，这便成了一个高度复杂的问题。首先在量测建模方面，Gilholm等人[1]提出了非齐次泊松点过程(PPP)，将目标数目建模为服从泊松分布模型，多个量测点分布在目标周围，这种模型具有数学上的方便，可以避免显式求解。在随机集理论(RFS)和PPP模型的基础上，Mahler在贝叶斯滤波的框架下推导并提出了扩展目标概率假设密度滤波器(Extended-Target PHD，ET-PHD)[2]。Karl等人在此基础上，将运动转移模型假设是线性的，同时假设观测噪声服从高斯分布，从而可以得到算法的闭合解，便可在已有的卡尔曼滤波理论框架下求得滤波器的快速迭代方程，进一步发展了概率假设密度滤波器在扩展目标跟踪领域的应用[3]。

随着RFS理论在EOT问题上的引入，相关研究成果便层出不穷[4-6]。基于RFS的PHD方法被认为是实现EOT问题的一种有效技术手段[7-9]，然而现有方法大多是基于线性高斯模型的，而实际中大部分情况都是非线性非高斯的。虽然将粒子滤波方法引入，提出的SMCPHD滤波器能够很好地处理非线性问题，但是计算量也是算法应用的一大瓶颈。近年来，有研究人员将区间分析技术和粒子滤波进行结合，提出了一种被称为盒粒子滤波(Box Particle Filter，BPF)的算法。与传统的粒子滤波采用误差统计模型不同，盒粒子滤波采用盒粒子和误差界限模型对量测点进行建模表示，经过这样处理后可以大幅降低所需要的粒子数，对粒子滤波固有的运算复杂度较高的问题具有较好的改善作用。近几年，很多研究者已经将区间分析技术用于跟踪问题并取得了很好的效果[10-11]，先后提出基于盒粒子的单目标Bernoulli算法[12-14]、基于盒粒子的单扩展目标Bernoulli算法[15-17]以及基于盒粒子的多目标PHD滤波算法[18]等。上述方法虽采用了区间分析理论，但是依然处理的是点量测数据而实际复杂场景下我们得到的数据一般都包含有较大的测量误差，采用区间量测进行表示可以更好地容纳这种不确定性。

对此，本文提出了一种基于BPF的多扩展目标伯努利滤波算法(ET-BP-MeMBer)。在区间量测的假设前提下，改进了伪似然函数，并针对存在的区间量测集划分问题，将相互距离度量用于近邻传播聚类算法，提出了基于MD-AP聚类的区间量测集划分方法。

1 盒粒子滤波

考虑如下非线性系统模型：

xk+1=f(xk,ωk)

(1)

zk=h(xk,vk)

(2)

式中，xk为扩展目标的状态，ωk表示过程噪声，vk表示量测噪声，f(·)为非线性状态转移函数，h(·)为量测方程，zk为扩展目标的观测值。

对于如上的非线性跟踪系统，广泛采用粒子滤波算法进行求解。但是粒子滤波算法并不是十全十美的，粒子退化、计算量大等问题仍然制约着该算法的发展。近年来一种被称为盒粒子滤波的方法得到了广泛地研究。

盒粒子滤波算法采用占据一定空间且面积可控的矩形区域来代替传统的点粒子去描述目标的状态分布。基本的算法过程如图1所示，简述如下：

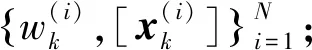
2)状态预测：k+1刻目标的预测概率密度函数为：

(3)

p(zk+1|xk+1)=U[zk+1](g(xk+1))

(4)

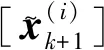
(5)

(6)

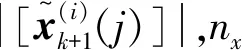
(7)

5)重采样：为了保持盒粒子多样性，必须进行重采样，由于处理的是带误差的数据，传统的适用于粒子滤波的重采样算法无法适用，本文采用随机子划分进行处理。

由于观测不确定性以及未知的各类偏差导致量测数据常常表现为区间的形式，如a=[a-,a+]。在这种条件下，传统的算法难以适用，便迫切需要寻求合适的滤波算法。

2 本文算法

本章首先对扩展目标伯努利滤波算法的大致过程进行简要介绍，接着详细叙述本文所提算法的主要过程。

2.1 扩展目标MeMBer滤波

在线性高斯的条件下，文献[13]对扩展目标MeMBer滤波算法进行了高斯混合实现。首先对传统ET-MeMBer滤波算法的跟踪过程简述如下：

1)预测

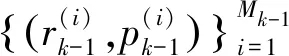
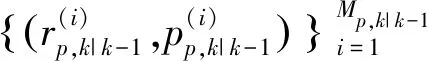
(8)

式(8)中，

(9)

(10)

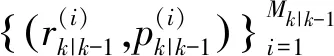
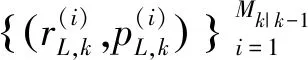
(11)

式(11)中，

(12)

(13)

(14)

(15)

2.2 基于盒粒子滤波的扩展目标MeMBer算法

上述2.1节给出了标准的ET-MeMBer滤波跟踪算法，但是在实际应用中，各种复杂因素常常导致产生不确定性量测，上述算法便无法处理。除此之外，在利用粒子滤波实施该算法时，为保证滤波精度，需要大量的粒子来覆盖目标的后验概率密度，增加了算法的运算复杂度。针对上述问题，本文假设量测为区间的形式，将盒粒子滤波方法代替粒子滤波方法，提出了ET-BP-MeMBer滤波算法，具体算法步骤如下：

步骤1 预测

设k-1时刻的多扩展目标PDF可表示为：

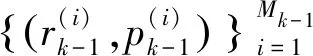
(16)

(17)

则预测PDF为：

8月28日，湖北省发改委已正式同意“东风汽车集团股份有限公司在武汉市建设乘用车扩建项目”，据了解，该项目将用于提升东风日产的在华产能，但是具体运营模式仍处在内部探讨阶段。新工厂位于武汉经济技术开发区凤凰工业园，分两期建设，年产能30万辆，能够生产包括乘用车（含传统燃油车和纯电动车型）及其他类乘用车（含传统燃油车和混合动力车型），建设期为2019年1月至2022年12月。该项目总投资为98.51亿元，其中东风公司持有66.86%的股份。

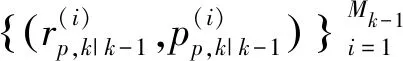
(18)

步骤2 更新

假设k时刻预测为：

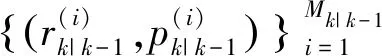
(19)

(20)

则更新的后验密度为：

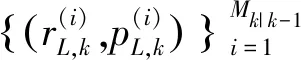
(21)

其中，

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

步骤3 约束传播

[x]=[x]×[xz]，[y]=[y]×[yz]

步骤4 重采样

为了保证粒子的多样性，以及区间粒子的特殊性，本文利用随机子划分的方法进行重采样。

步骤5 修剪与合并

随着迭代更新和目标数的增加，伯努利项数目将会越来越多，为了提高计算效率，同时避免虚假轨迹的干扰，需要对伯努利项进行删减处理，一方面避免了干扰，另一方面也降低了计算量。

步骤6 状态提取

仅提取概率大于0.5的伯努利分量，再利用传统的Kmeans算法进行聚类，从而获得目标的状态估计，即：

(31)

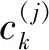
2.3 基于MD-AP的区间量测划分

AP算法是一种被广泛使用的聚类方法[19]。在区间量测的环境下，所有的数和矢量均以区间的形式给出，传统的度量方法难以适用，为此，采用一种新的度量方法称之为相互度量。

设a=[a-，a+]、b=[b-，b+]为两个区间量测，则将a相对于b的相互距离：

(32)

而b相对于a的相互距离：

(33)

式(33)中，(a∧b)=Max(a+,b+)-Min(a-,b-)。

由于a相对于b的相互距离并非总等于b相对于a的相互距离，为了适用于AP算法，本节定义a和b的相似性度量为：

(34)

设A=[a1,a2,…,an]、B=[b1,b2,…,bn]为两个区间矢量，则A相对于B的区间相似度为：

(35)

接着直接采用前文提过的AP算法，算法中要求的相似度矩阵采用相互距离来计算，这样便得到了适用于区间量测的划分算法，如下所示：

步骤1 采用相互距离构建所有量测点间的相似度矩阵，将代表矩阵和适选矩阵的元素都初始化为0：a(0)(i,k)=r(0)(i,k)=0；

步骤2 对建立的两个矩阵进行交替更新，当满足收敛条件时停止迭代，并通过对各个量测点进行计算寻找各自的中心点从而实现量测集划分；

至此，给出了基于MD-AP的区间量测划分主要步骤。与传统点量测集划分相比，区间量测集划分主要在于对区间量测点相似度的定义以及准则函数的确定上有所不同。

3 算法分析及仿真实验

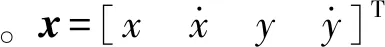
表1 目标初始状态和运动信息Tab.1 Target initial states and moving information

其状态转移密度为：

πk|k+1(x|x′)=N(x;Fx′,Q)

(36)

式(36)中，

Q=diag(0.01×I9，Qk)，Qk=diag(Q1,Q1)，

其中，I9表示9维的单位对角阵，T表示采样周期。

圆形目标半径R=20 m，则目标状态可表示为：

(37)

量测方程h(x)定义为：

(38)

图1给出了多扩展目标一次MC仿真的态势图，其中圆形表示目标，方块表示杂波和量测。图2给出了跟踪过程中目标数目的估计比较。可以看出，本文算法在对目标进行数据估计时波动更小，估计更稳定。

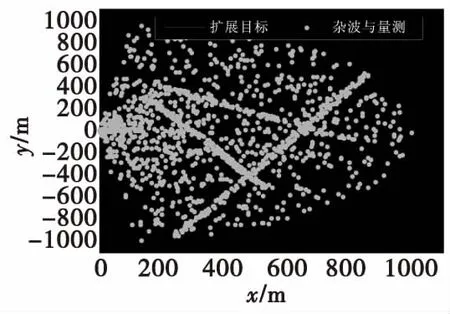
图1 态势图Fig.1 The situation of targets

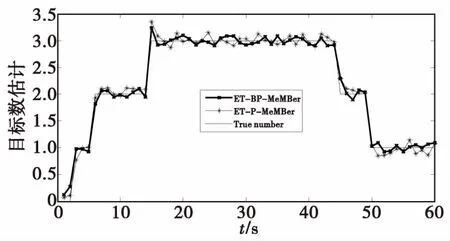
图2 目标个数估计图Fig.2 The estimated number of targets

为了对两种算法的跟踪性能表现情况进行充分比较，对算法进行了多次MCMC仿真实验，如图3-图6所示。

图3 平均OSPA距离与杂波的关系Fig.3 The relationship between the mean OSPA distance and mean number of clutters

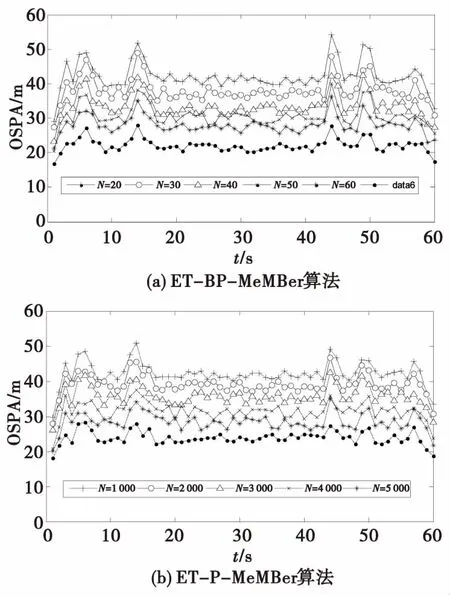
图4 两种算法OSPA距离与粒子数关系Fig.4 The relationship between OSPA distance and number of particles

图3表示算法平均OSPA距离随杂波的变化情况。从图中可以很明显地看出杂波对算法的性能有较大的影响，本文算法稍优于原始算法。但是值得注意的是，两种算法均不能达到对杂波的良好抑制作用。

图4对两种算法在不同粒子数下的平均OSPA进行了比较试验，其中图4(a)为本文所提算法，N表示设置的粒子数目。随着粒子数的增加，两种算法滤波的OSPA值都有逐步减少的趋势。但是可以看出，在近似的性能表现要求下，本文算法所需要的粒子数目远远小于基于点粒子滤波的方法。

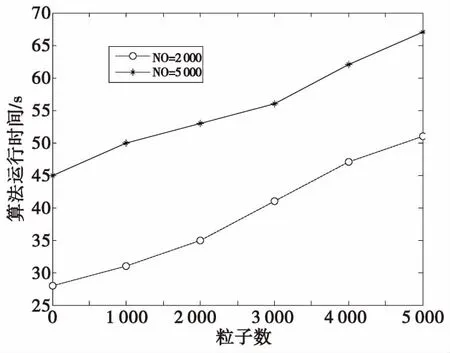
图5 ET-P-MeMber算法平均运行时间Fig.5 The average operation time of ET-P-MeMBer

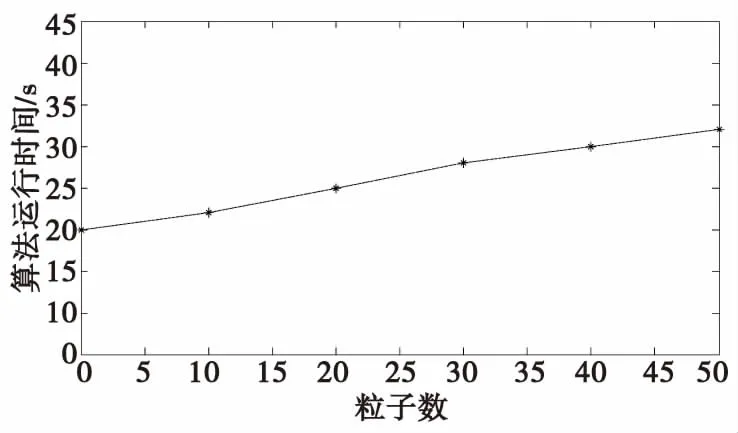
图6 ET-BP-MeMber算法平均运行时间Fig.6 Theaverage operation time of ET-BP-MeMBer

图5对算法的运行时间进行对比，主要通过在相同新生目标数的前提下，各自产生不同新生粒子数的情况。为了捕获新生目标，ET-P-MeMBer算法需要产生大量的新生粒子，使得运算量有所增加，而ET-BP-MeMBer算法的主要时间消耗在盒粒子滤波的区间运算上。综合来看，本文提出的ET-BP-MeMBer算法由于在运算效率和精度上有着良好的折中，使得可以更好地应用于实际场景中。

4 结论

针对不确定量测下的对扩展目标跟踪问题，本文提出了基于MD-AP的ET-BP-MeMBer算法。当量测采用区间表示的时候，传统的处理手段难以利用，本文将盒粒子滤波算法用于滤波求解过程，在建模了量测误差的前提下，较大地提升了算法的运算效率，同时本文提出了基于相互距离的AP算法用于处理区间量测集划分问题。实验结果表明本文算法有着较好的跟踪精度和计算效率。