Application of Genetic Algorithm in Estimation of Gyro Drift Error Model
2019-05-15LIDongmeiBAITaixunHEXiaoxiaZHANGRong
LI Dongmei, BAI Taixun, HE Xiaoxia*, ZHANG Rong
Department of Precision Instrument, Tsinghua University, Beijing 100084
Abstract: Extended Kalman Filter (EKF) algorithm is widely used in parameter estimation for nonlinear systems. The estimation precision is sensitively dependent on EKF's initial state covariance matrix and state noise matrix. The grid optimization method is always used to find proper initial matrix for off-line estimation. However, the grid method has the draw back being time consuming hence, coarse grid followed by a fine grid method is adopted. To further improve efficiency without the loss of estimation accuracy, we propose a genetic algorithm for the coarse grid optimization in this paper. It is recognized that the crossover rate and mutation rate are the main influencing factors for the performance of the genetic algorithm, so sensitivity experiments for these two factors are carried out and a set of genetic algorithm parameters with good adaptability were selected by testing with several gyros' experimental data. Experimental results show that the proposed algorithm has higher efficiency and better estimation accuracy than the traversing grid algorithm.
Key words: genetic algorithm, traversing grid algorithm, coarse grid optimization, gyro drift error model, crossover rate and mutation rate selecting
1 INTRODUCTION
The gyroscope is a high-precision angular sensor which directly determines navigational system performance. Therefore,the estimation precision for gyro drift error model is very important for the navigation system[1].
The gyro drift model is nonlinear, so Extended Kalman Filter(EKF) algorithm is used for parameter estimation. Its estimation precision is sensitively dependent on the initial state covariance matrix and state noise matrix of EKF[2].
A two-stage method, coarse grid followed by fine grid, is used in the current optimization. Since coarse grid optimization takes long time, we proposed a scheme with a genetic algorithm for the coarse optimization to further improve calculating efficiency. Based on tests with experimental data from several gyros, a set of adaptive genetic algorithm parameters were selected. Genetic algorithm with these parameters was used for testing and compared with the results using traversing grid algorithm. The comparison results confirmed the efficiency and accuracy of genetic algorithm method.
In section 2, the gyro drift error model and optimization criterion are introduced. Then the basic principle of the two-stage grid optimization method used in the current gyro drift test and the proposed genetic algorithm and its implementation steps are described in section 3 and 4 respectively. Experimental results are compared and analyzed in section 5. The conclusion and discussion are given in the final section.
2 GYRO DRIFT ERROR MODEL
The gyro is tested on a servo-turntable and initially oriented to the geocentric coordinate system. Its drift error model with case rotating-dwelling auto compensation device is[3]:
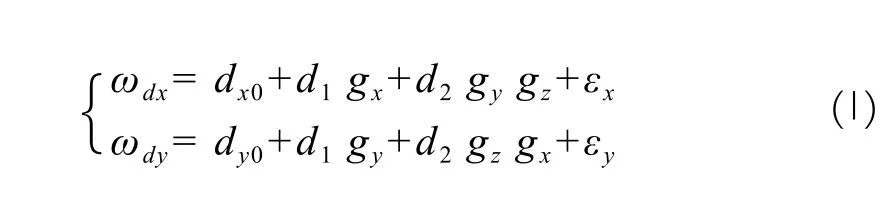
In the above formula, εx, εyare gyro random drifts. gx, gy,gzrepresent the projection of the gravity acceleration in the three-axis direction of the gyro coordination. dx0, dy0,d1, d2are the model parameters to be estimated. wdx, wdyare drift rate which can be calculated by the frame angles θx, θyof the servo-turntable.
Because gravitational acceleration in gyro coordination is nonlinear with frame angles, the gyro model system is a nonlinear system and EKF is used to estimate model parameters. State equation and observation equation for the EKF are as follows[2]:
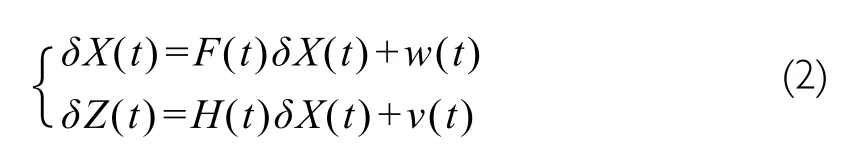
where w and v are mutually independent and normally distributed white noise. F(t) represents the state transition matrix and the other parameters are as follows:
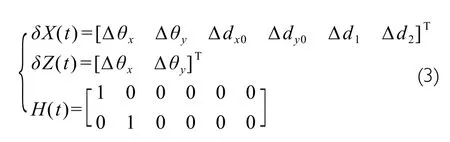
The discrete nonlinear Kalman filter equation is[2]:
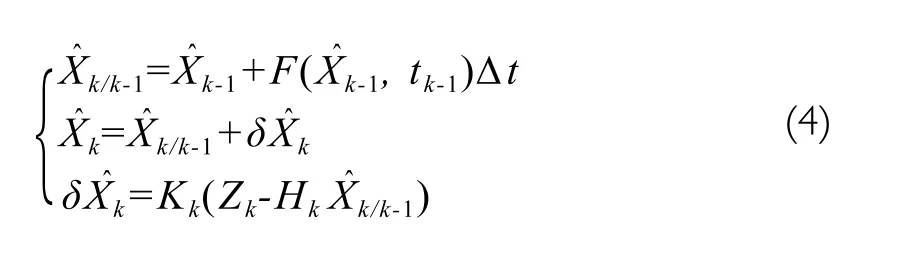
where Zkis the measurement at time k, Kkthe Kalman filter's gain,the state correction value, the state prediction value, Δt the discretization period. Ksis iteratively calculated by the following formula.
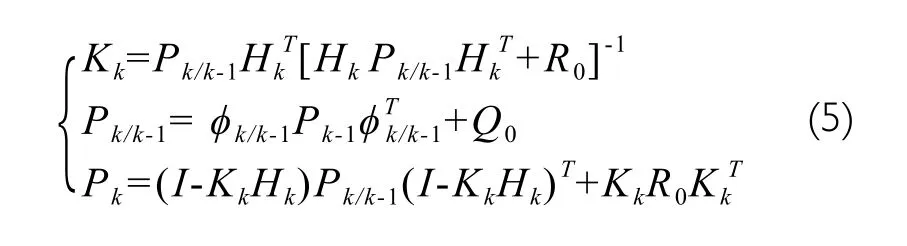
The state estimation covariance matrix represents the accuracy of the state estimation. The system has six state quantities,so the matrices P0and Q0are both 6×6 diagonal matrices.Therefore, there are 12 matrix parameters to be optimized.The criterion of optimization is the linear combination of the final random drift and the fluctuation of all the model parameters'which is formulated by the objective function
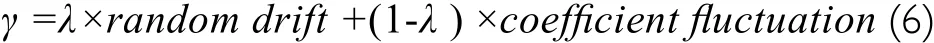
where λ is the weight with range of [0,1].
3 INTRODUCTION TO GRID OPTIMIZATION METHOD
The grid optimization method is commonly used in parameter optimization problems, and the basic principle is traversal search. Its basic steps are to divide the range of parameters into grids, then calculate the objective function point by point and finally select better parameters by comparing all the grid points.In theory, as long as the grid is fine enough, the optimal parameters can be found within reasonable tolerance[4].
The currently used method is two-stage method, coarse grid followed by fine grid, as shown in Figure 1. In each step,two parameters are selected from the 12-dimentianal optimization space to minimize the objective function, then these two states are updated, and another two different parameters are selected in the next searching step.
Supposing the optimization space be divided into n×n grids,the parameter optimization range is [start, end ], and s represents the value on grid point. The specific calculation method of the grid search algorithm is
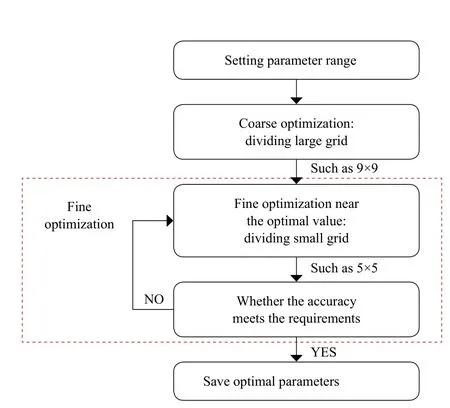
Figure 1 Flow chart of coarse and fine two-stage grid method
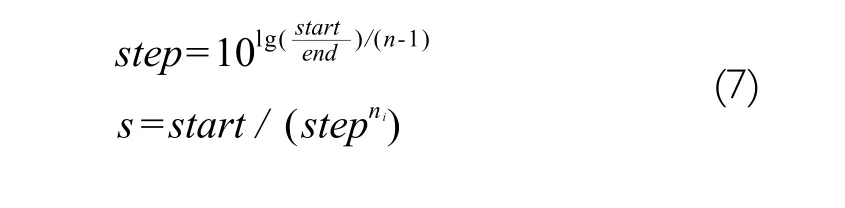
wherestepis grid size. The parameternwith range of [ 0,n- 1] is the index of grid point.
Coarse and fine grid methods can reduce the calculation task and computation time. However, as the sample space or the number of parameters to be optimized increases, the amount of calculation will still be very large.
4 THE BASIC PRINCIPLE OF THE GENETIC ALGORITHM AND ITS IMPLEMENTATION METHOD
The genetic algorithm solves the parameter optimization problem by simulating the biological evolution on a computer.The basic theory is Darwin's biological evolution theory. The genetic algorithm improves the adaptability of the individual to find the optimal solution through selection, crossover, mutation and other processes[5].
According to the experimental result, fine grid optimization takes far less time than coarse grid optimization, so we use the genetic algorithm in the coarse optimization.
The genetic algorithm is mainly composed of gene coding,population size, fitness function and genetic operators as shown in Figure 2.
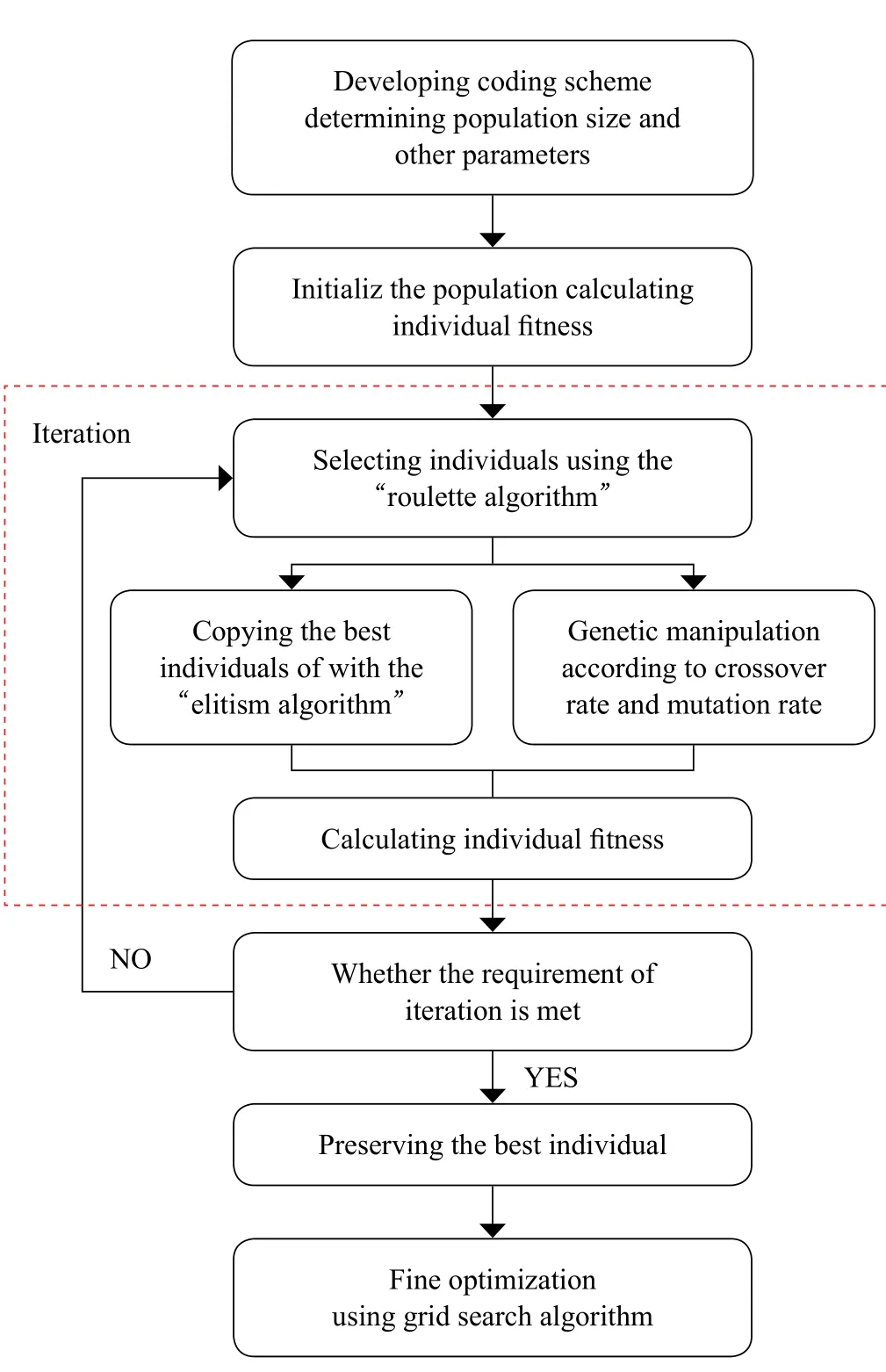
Figure 2 Flow chart of genetic optimization algorithm
The purpose of gene coding is to convert the practical problem into a computer-solvable genetic problem. The coding method adopted in this experiment is binary coding. The coded parameter isniin the grid optimization method in formula (7).For example, if the grid is divided into 16×16, the value range ofniis 0 - 15.
Since two parameters are selected each time for model calculation, the length of an individual is set to eight-bit gene which represents the 16 values ofni. The first four bits represent the first parameter, while the last 4 bits represent the second one.
The size of the population may affect the complexity and performance of the genetic algorithm. Too small population cannot reflect the diversity of organisms, while too large population will increase the complexity of the algorithm. Based on experience and multiple experiments, the population is set to 5.
Fitness function is the criterion to guide how the genetic algorithm evolves, the key to measure the pros and cons of the algorithm. The higher the individual's fitness, the greater survival probability the individual will have. Usually, the fitness function of the individual is set as a linear combination of the objective function. The purpose of this paper is to minimize the objective functionYin formula (6), so (1-Y) can be used as the fitness function.
Genetic operators consist of three basic operations: selection, crossover and mutation.
The purpose of the selection operation is to select the best individuals for crossover and mutation operation so that the next generation of genes are more outstanding. To implement the selection operation, the first step is to calculate the individual fitness, and then select individuals based on fitness ratio or fitness order. The strategy adopted in this paper is proportional selection, that is, the probability that an individual is selected is proportional to its fitness. The specific implementation algorithm adopts the “roulette algorithm” with formula as follows[5]:
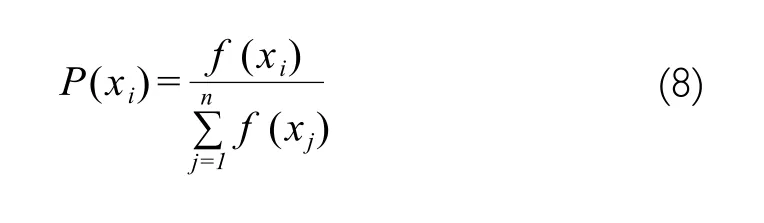
In order to prevent the optimal solution from being destroyed by crossover and mutation during the process of genetic evolution, the elitism algorithm is used to copy the best individual in each generation to the next generation[6]. In addition,if the fitness of the worst individual in the current generation is worse than the best in the previous generation, the worst individual in the current generation will be replaced by the best in the previous. In this way, the population size is kept constant.
Crossover operation simulates the phenomenon of gene recombination in nature, that is, the selected individuals exchange part of the genes to form new individuals according to the crossover operator. Genetic recombination is the main method to generate new individuals, which determines the global search ability of genetic algorithm. Commonly used crossover operators are single-point crossover, two-point crossover, uniform crossover, fusion crossover and so on.
Since an individual's eight-bit genes represent two independent parameters, we use two-point crossover method here,that is the first four genes and the last four genes of two individuals each subjected to a single-point crossover. The crossover operation is carried out with a certain probability, called the crossover rate. Based on experiments' result, the crossover rate is set to 0.8.
Mutation operation simulates the phenomenon of gene mutation in nature, that is, an individual's genes are mutated according to a certain probability to form a new individual. Gene mutation is an assistant method for generating new individuals,which determines the local search ability of genetic algorithm.Commonly used mutation operators include basic bit mutation,uniform mutation, quadratic mutation, Gaussian mutation and so on.
In this paper, the random uniform mutation is adopted where an individual randomly is selected and a random gene position is mutated to 0 or 1. The mutation operation should also be carried out with a certain probability, which is called the mutation rate. Based on experiments' result, the mutation rate is set to 0.2.
Genetic algorithm requires iterating continuously to get optimal results till the termination rule is met. Commonly used termination rules include iteration limit, calculation time limit,objective function limit and so on. In this paper, the number of iterations is used as the termination rule. After many experiments, the number of iterations found to be better within 25.
5 EXPERIMENTAL RESULTS
We conducted the experiments with the following steps:
Step 1. Initialization
Genetic algorithm parameters are selected as Table 1 shows. The parameter range of matrixP0for coarse optimization is [1e - 5, 1e5] and the parameter range of matrixQ0is [1e- 10, 1e2].
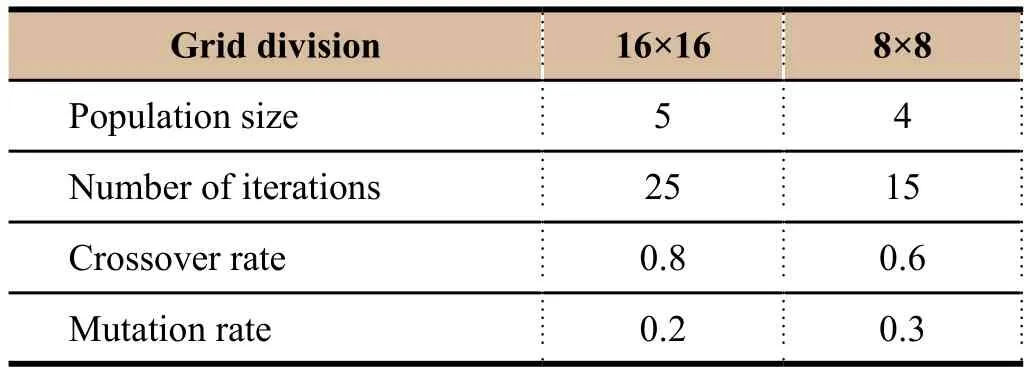
Table 1 Genetic algorithm parameters
In addition, the selection operator adopts the proportional selection - roulette algorithm. And the elitism algorithm is used to copy the best individual in each generation to the next generation.
Step 2. Coarse and fine optimization
The genetic algorithm with the above parameters is embedded into the coarse optimization process of the traversing grid algorithm. The grid divisions with 16×16 and 8×8 are both conducted. The fine optimization process still uses the grid optimization method. The grid division for fine optimization is 5×5.
Step 3. Estimation
Based on the above settings, the Extended Kalman Filter algorithm is used to estimate the parameters of gyro drift error model. The coefficient fluctuation is represented by the standard deviations during the last three hours of the filtering process. The random drift is represented by the prediction error.
With these steps, we obtained the comparison results of efficiency shown in Table 2 and Table 3 and comparison result of accuracy shown in Table 4. All the experimental results have been normalized.
Considering the randomness of the genetic algorithm, all the experimental tests of the genetic algorithm are carried out three times.
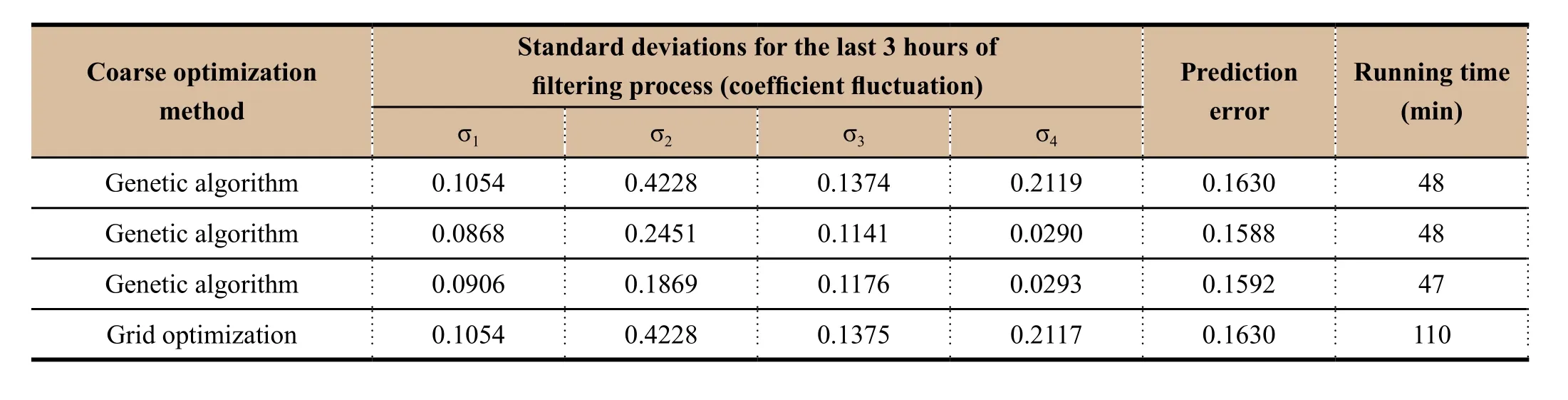
Table 2 Efficiency comparison of optimization algorithms (mesh divided into 16×16)
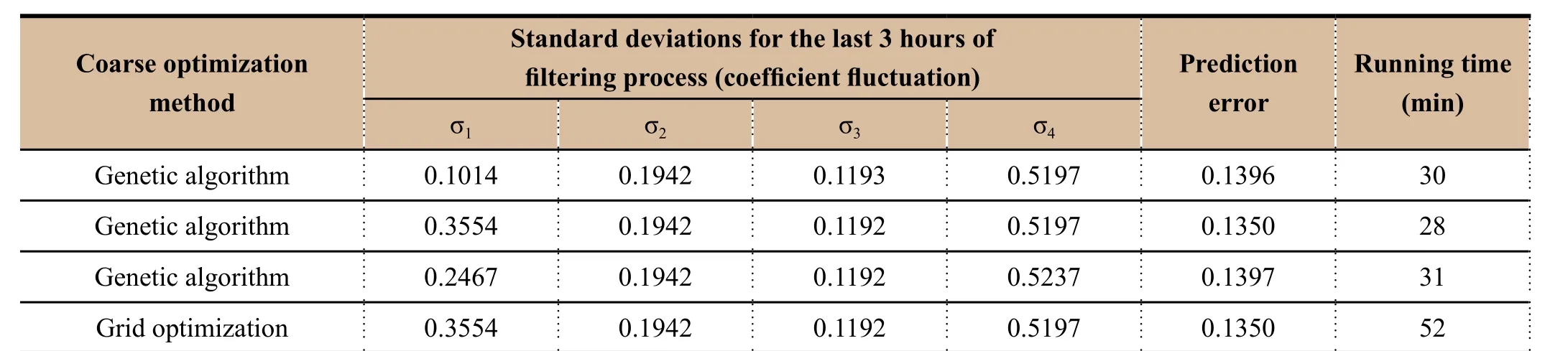
Table 3 Efficiency comparison of optimization algorithms (mesh divided into 8×8)
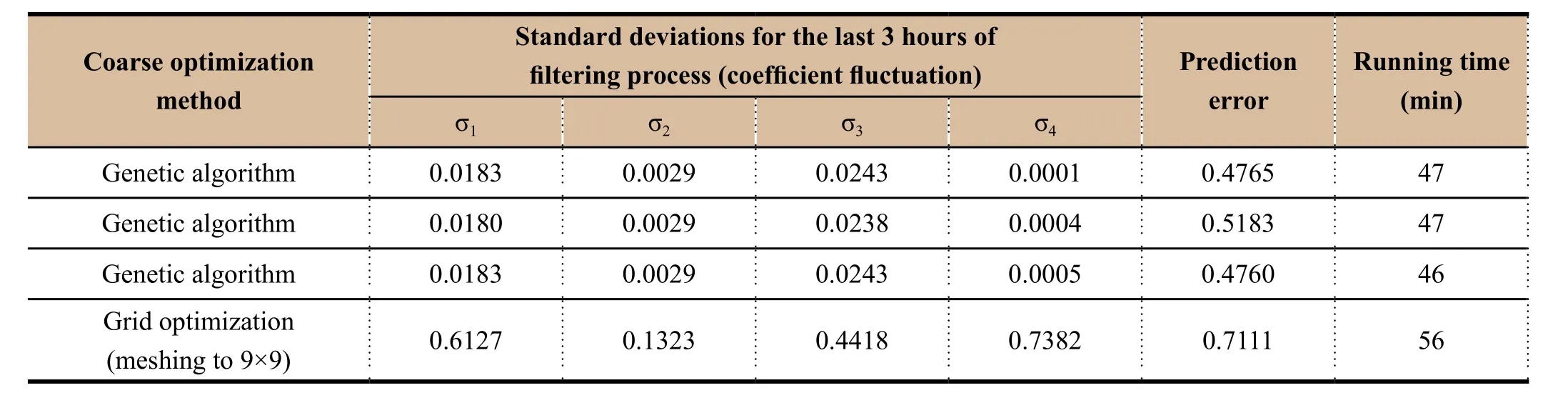
Table 4 Accuracy comparison of optimization algorithms (compared with traversing algorithm)
From the comparison results in Table 2 and Table 3, it can be seen that the genetic algorithm result is better or with equal effect to traversing gird algorithm, while the processing time is shortened. We can conclude that the new algorithm can meet the accuracy requirements of parameter optimization and improve the efficiency by 40% - 50%.
From the comparison results in Table 4, it can be seen that the result using the new algorithm is more accurate than traversing algorithm. The coefficient fluctuation is reduced by at least one order of magnitude, while the prediction error is also improved. The running time is also shortened. Therefore, the genetic algorithm in this paper can improve both efficiency and accuracy.
In summary, in the optimization of gyro drift model parameter, the grid optimization method based on genetic algorithm can improve the efficiency of the algorithm without loss of estimation accuracy compared with the traversing method. In the case of the same process time, the new algorithm can also improve the estimation accuracy.
6 CONCLUSIONS
In this paper, the two-stage grid optimization method for the gyro drift model is introduced, and the basic principle and implementation process of the genetic algorithm are described in detail. In order to simplify the complexity and shorten the running time of the program, the genetic algorithm is used to replace the coarse optimization stage of the traversing grid method. Based on experimental test, we can conclude that the running time of the genetic algorithm is shortened by 40% -50% without loss of the estimation accuracy.
In this paper, the method is only used in optimization for two-dimensional space. Its efficiency and accuracy used in higher dimensional space should be further studied.
杂志排行
Aerospace China的其它文章
- Numerical Simulation of Unsteady Flow of Reentry Capsule
- Analysis and Solution of Multipath Effect on Wireless Communications of Launch Vehicle
- CFOSAT-1 Realizes First Joint Observation of Sea Wind and Waves
- Application Advantages of Staring Area Imaging Technology (SAIT) for Microsatellites
- Analysis of China's Nano andMicrosatellite Industry Development
- XUE Huifeng Attended the IAA Spring Meetings
