基于Drucker-Prager模型的振动压实有限元分析及试验研究

马丽英， 李茂其， 王 维， 曹源文

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

公路交通在地域的经济增长中扮演着重要角色。JTGF801—2017在《公路工程质量检验评定标准》中，在道路检测项目中，压实度为最重要的评价指标[1]。可见公路的质量很大程度上取决于压实效果。传统压实度检测是在压实完工后对少部分路段进行检测，其代表性差、费工费时、破坏结构。随着对施工作业效率要求的逐渐增加，而传统检测方法难以实现对压实质量的实时检测[2]。因此，为实现压实度实时检测，研究土壤与振动压路机振动轮动态响应关系和压实特性，变得尤为重要。

多年来国内外对振动轮与土体的相互作用做了大量的研究。邱声等[3]在仿真软件中建立了振动轮-土壤模型，并对其进行仿真分析，为研究振动压路机压实特性提供了新的方法；黄志福等[4]从动力学角度出发建立了振动压式系统模型，得到了振动轮加速度与与路面材料刚度系数、阻尼系数的关系；J. MACIEJEWSKI等[5]研究了振动压实的激振力、激振频率和钢轮轮重等压实参数对黏性土壤压实度的影响，结果表明土壤压实度受钢轮质量的影响最大；T. HIROMA等[6]考虑了土壤与振动轮之间的摩擦，并利用仿真软件对振动轮-土壤模型进行分析，结果表明接触面上正应力和切应力的分布受钢轮滑转率的影响

1 土壤的本构模型

1.1 屈服准则

岩土材料的力学性质更多使用Mohr-Coulomb屈服准则来描述，控制方程为

(1)

式中：σ1为第一主应力；σ2为第二主应力；σ3为第三主应力；c为黏聚力；φ为内摩擦角。

但是中间主应力对屈服和破坏的影响Mohr-Coulomb准则不能体现。而且Mohr-Coulomb准则在偏平面的屈服面为六棱锥面，角隅处塑性应变增量方向不唯一，导致在进行塑型分析时会不易收敛，不利于数值计算。而Drucker-Prager构造了一个光滑没有棱角的屈服曲面内切于M-C准则的六棱锥面，提出了D-P屈服准者[7-8]，其函数形式为

(2)

式中：I1为应力张量第一不变量；J2为应力偏量第二不变量，即：

(3)

I1=σ1+σ2+σ3

(4)

(5)

(6)

1.2 确定土壤本构模型

在ABAQUS中提供的拓展D-P准则、M-C准则和经典D-P模型在偏平面的屈服线如图1。

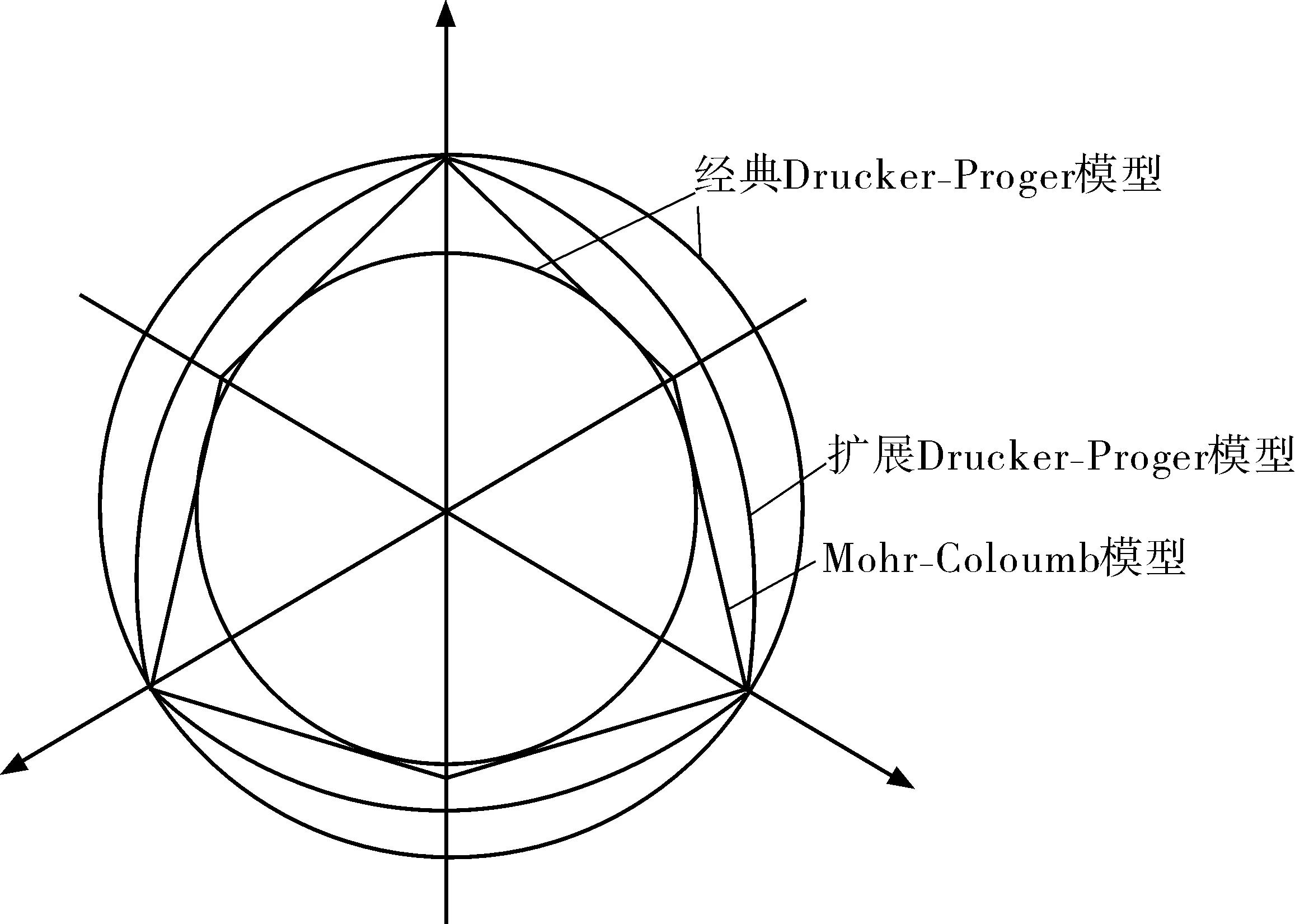
图1 π平面上不同屈服准则对应的屈服线

下面对线性D-P模型和M-C模型的适用范围和关系进行分析。

将线性D-P和M-C进行同样的拉伸和压缩破坏定义，则线性D-P模型可以使用另一种形式表达[8-11]。

三轴拉伸时：

(7)

三轴压缩时：

(8)

对于所有的(σ1，σ3)，若要将M-C模型控制方程(1)与公式(7)、公式(8)中的方程保持一致，需要使。

(9)

(10)

(11)

根据以上方程可以求出K值：

(12)

式中：K为三轴拉伸强度与压缩强度比值。

当K=1时，屈服面在偏应力平面内为Von Mises圆，此时三轴拉伸时的屈服应力相等与压缩时的屈服应力；当K≥0.778时，屈服面是外凸的，此时由式(12)可知，需要使φ≤22°，也即当摩擦角≤22°时，两个模型能很好的进行拟合，此时用D-P模型进行分析计算效果较好；当摩擦角>22°时，仿真模型不能很好的拟合，此时使用M-C塑性模型可得到较好的拟合效果。

通过试验测定，可以较为简单的得到M-C模型的土体参数。而D-P模型则克服了M-C模型的种种弊端，但是其模型参数需要从M-C模型换算得到。

当摩擦角>22°时土体单元应使用M-C模型，当摩擦角≤22°时土体单元应使用D-P模型，因此在文中土体单元使用D-P模型较为合适。

2 有限元模型

2.1 模型参数的确定

压路机振动轮由多个机构组成，振动时通过液压装置驱动钢轮中的偏心块运动，偏心块高速旋转产生的离心力迫使钢轮振动进而对土壤进行压实[12]。在有限元中，结构复杂不仅会导致建模困难，而且使得计算量增大、不易收敛，所以应对模型进行简化。在模型中将振动压路机的前轮分配质量直接体现在振动轮上，将振动产生的激振力作用在轮的质心上。

土壤有限元模型尺寸的选取应考虑压路机施工速度、模型分析时间及压实土体几何参数等因素。综合分析得出土壤有限元模型的最佳尺寸为：20 m × 8 m × 0.8 m。

本研究中选用徐工集团的XD82E型振动压路机。该压路机的主要参数如表1。

表1 压路机主要参数

2.2 材料参数的确定

振动轮的材料参数可直接由压路机型号直接查到，在模型中振动轮取φ=7 600 kg/m3，泊松比μ=0.28，振动轮的弹性模量E=210 GPa。

依托江西省交通厅项目，采用试验研究与经验相结合的方法来确定在同一路段中第3、第5和第7遍压实下土壤的参数，结果如表2。

表2 土壤主要参数

研究发现，在压实作业时，最初土壤发生弹塑性变形。随着土壤的压实，土壤的塑性变形逐渐减少。当土壤得到完全压实时，土壤仅仅发生弹性变形。因此，将弹塑性考虑到土壤模型构建中，其弹性与塑性分别由线弹性模型与Drucker-Prager模型组成。

2.3 有限元划分

有限元规划的难易程度与计算的速度、收敛性以及精确度密切相关。土壤采用缩减积分的C3D8R单元，共120 000个单元。

振动轮利用C3D4单元，共2 000个单元。土壤隶属为半空间无限体，有限元模型主要解决有限区间问题，通常在建模中，对土壤采取截断措施，致使压力波由于阻挡作用而不能进行长距离传送，在到达拦截处返回，从而对计算精度进行干扰。因此，在拦截处采用具有改善精度与准确度的黏性人工边界的方法，进而缩减拦截处对无限空间的波动干扰。建立的“振动轮-土壤”模型如图2。

图2 振动轮-土壤有限元模型

3 有限元模型的仿真分析

3.1 轮下土壤应力分布特性分析

依据上文已知的模型、材料参数对有限元进行分析，得到了土壤应力分布云图如图3，土壤竖向应力分布路径曲线如图4。

图3 土壤应力分布云图

由图3可知，有限元模型构建的土壤内部竖向应力变化范围与振动轮轴向延伸形状具有相似性，同时由振动轮与土壤的接触面由浅至深沿椭球面的方向，土壤的竖向应力越来越小。土壤垂向最大应力表现为振动轮轮轴竖向位移上，并沿轮宽指定方向呈现对称分布，垂向应力沿振动轮移动方向体现为非对称发散状况，同时垂向力沿振动轮前进方向应力变大。

由图4可知，竖向应力的大小在土壤表层振动轮轮宽的距离内分布较为均匀，基本没有变化。其分布间隔长度高于振动轮宽度时，其竖向变应力迅速减小，因此对振动轮进行模型构建时，由于没有对端面进行倒角操作，所以振动轮与土壤接触线两端的土壤表层会发生应力集中。即使加入倒角，会一定程度的减弱应力集中现象，但仍会发生。在振动压实中，土壤吸收振动能量发生塑性变形，土壤的竖向应力会随着土壤深度的增加而减小，分布曲线也会变得平坦，并沿着振动轮轴向呈现抛物线分布，且应力集中随着土壤深度的增加而逐渐消失。

图4 振动轮轴向土壤应力分布路径曲线

3.2 土壤参数对振动轮竖向加速度的影响分析

则由上述可得，其振动轮参数保持一致，同理对土壤Ⅰ、土壤Ⅱ和土壤Ⅲ进行有限元分析，得到结果的加速度曲线如图5。

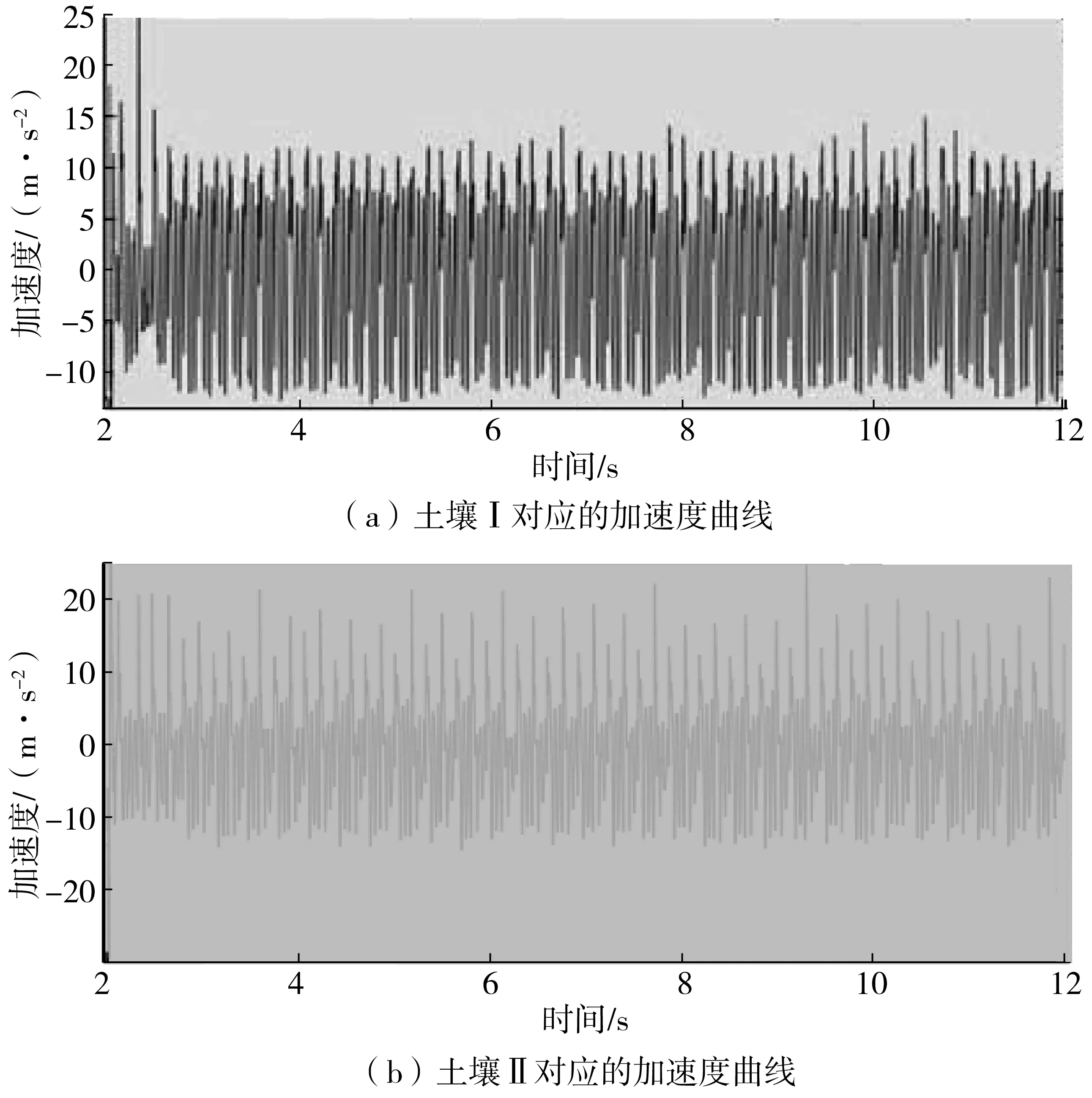
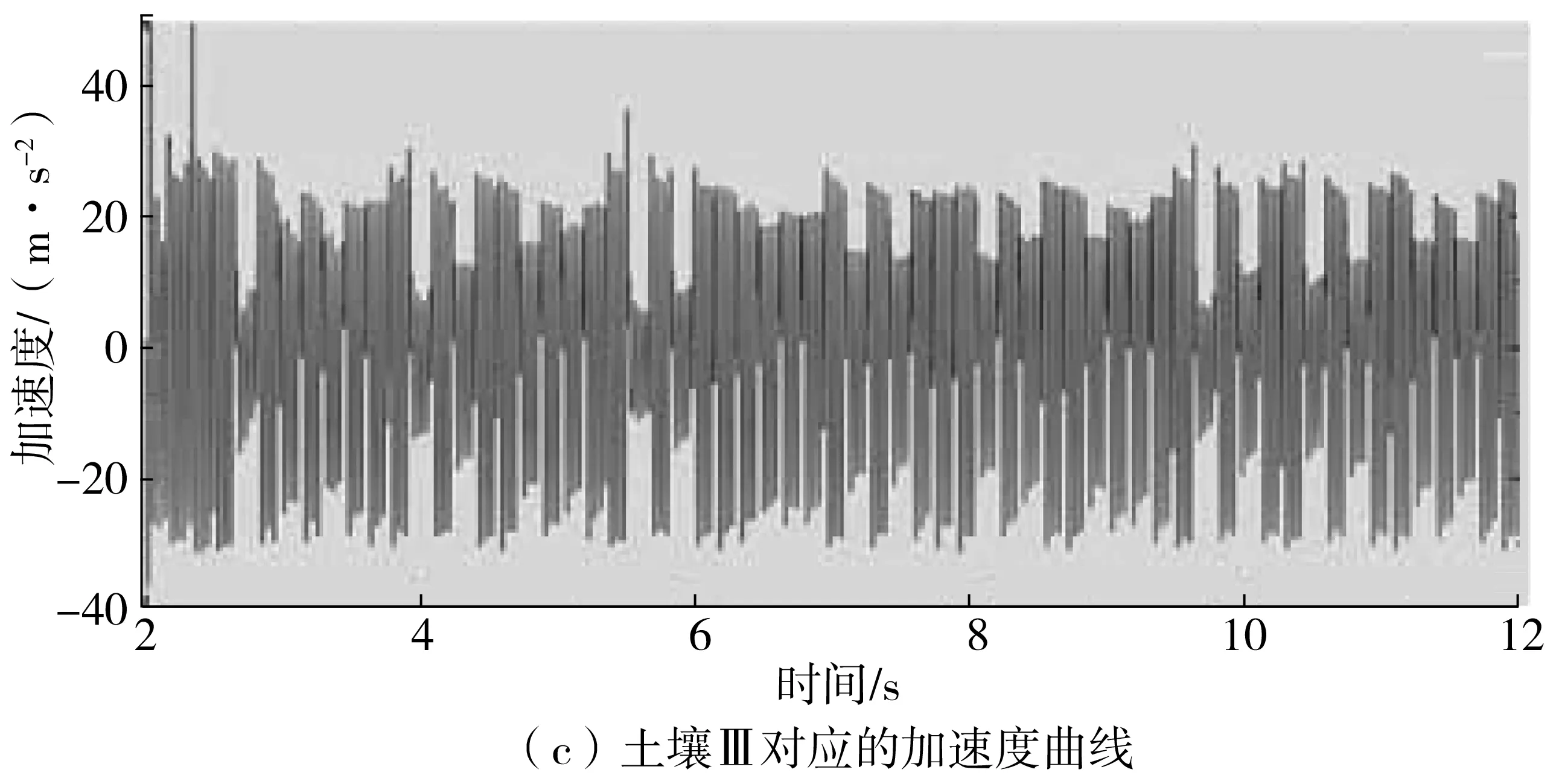
图5 振动轮竖向加速度曲线

由图5可知，振动轮启动的瞬间会在相反的方向上产生较大的加速度，随后振动轮垂直加速度先变大然后逐渐趋于平稳状态。土壤的参数、压实遍数对振动轮的垂直加速度幅值有一定程度的影响，如图5(c)中的加速度曲线所示，加速度幅值变化不存在一致性，振动轮的振动不规律。这是因为压实遍数的增加，此工况的土壤压实度已经达到最优值。

4 试验验证

为了验证有限元模型的正确性，进行了试验验证。测试的主要项目有：压路机工作速度，振动轮竖向加速度及路基压实度。

由于振动加速度的周期较短，通常只有0.02～0.05 s，且压路机工作速度较慢，所以我们取20个周期信号为对象。在对振动加速度信号进行滤波去燥、消除趋势项等预处理后，计算20个周期信号的加速度有效值，并将在一遍压实作业中的加速度有效值的平均值作为此遍的加速度值，并用灌砂法测出每一遍压实后路基的压实度值。加速度、压实度与压实遍数的关系如图6，加速度与压实度之间的关系如图7。

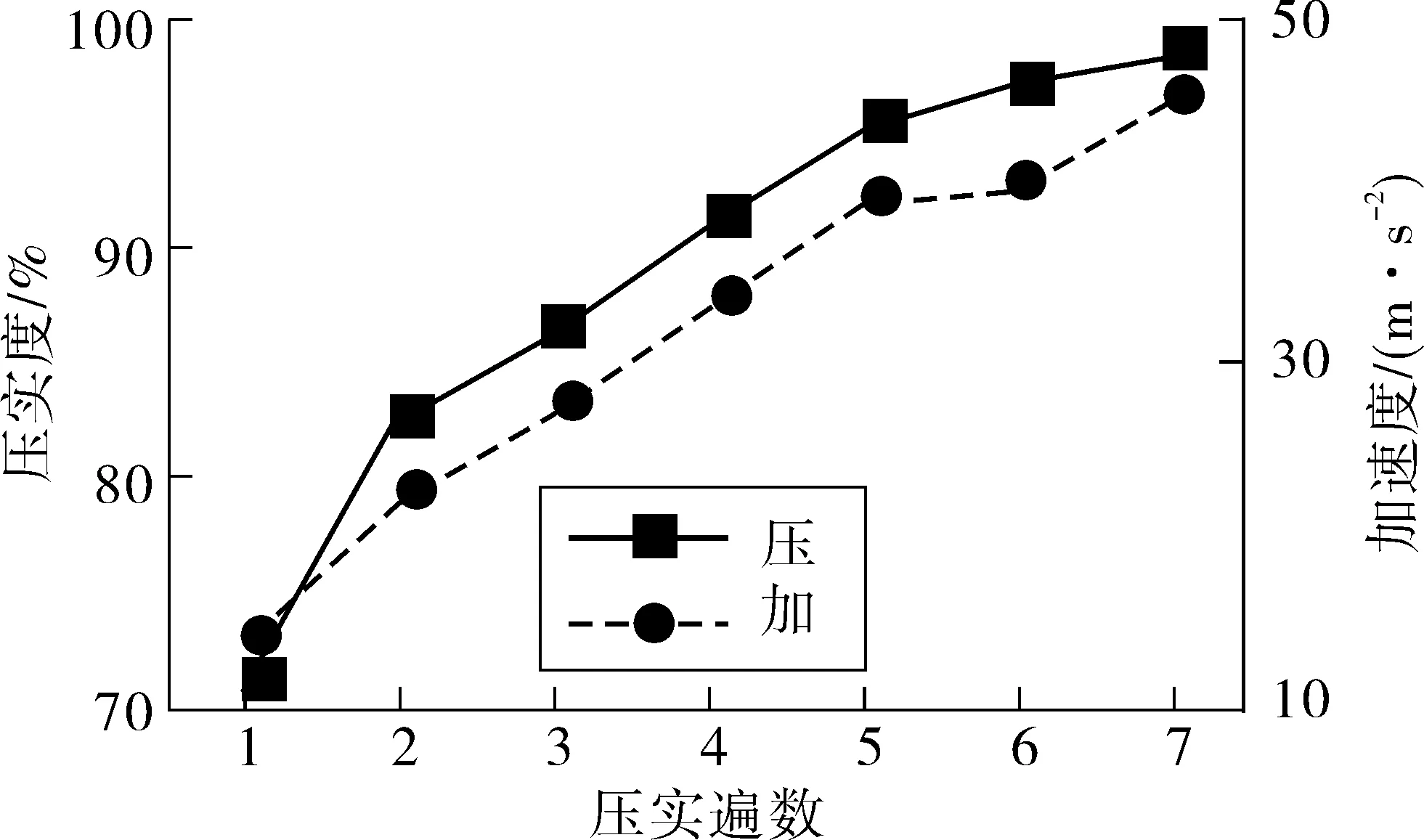
图6 加速度、压实度与压实遍数的关系

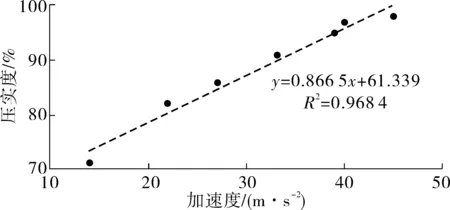
图7 加速度与压实度的关系

由图6可知，振动轮的竖向加速度与压实遍数呈正相关，与模型得出的结论基本吻合。且压实度随着压实遍数的增加也在增加。

对加速度与压实度进行进一步分析,对图7中的点进行线性拟合可得：

y=0.866 5x+61.339，R2=0.968 4

式中：y为压实度；x为加速度；R2为决定系数。

两者的相关系数为0.968 4，说明振动轮的竖向振动加速度与压实度的相关性良好，故可对加速度进行监测然后利用振动轮加速度与压实度的相关关系式获得压实度值。

5 结 论

1)讨论了D-P线性模型和M-C模型的相关性及应用条件，当摩擦角≤22°时，两个模型能很好的进行拟合，土体单元应当用Drucker-Prager模型进行分析，效果较好;当摩擦角>22°时, 两个模型的拟合效果不佳，土体单元应当直接用Mohr-Coulomb模型。

2)利用ABAQUS建立了“振动轮-土壤”的复合有限元模型，在压实遍数增多的情况下，分析了振动轮垂直加速度及土壤的垂直应力分布特性的变化。由分析结果可知：土壤的垂直应力在振动轮轴向方向上分布对称，沿着振动轮前进方改变，随着土壤深度的增加，在土壤的垂直方向上的应力显著减小。在振动压路机的最佳工况范围内，激振力和激振频率处于稳定状态，振动轮垂直加速度跟压实遍数存在一定的相关性。

3)试验表明，采用Drucker-prager弹塑性模型来模拟进行振动轮下土体的力学特性是可行的，笔者建立的振动轮-土体有限元模型基本正确。且加速度有效值与压实度之间也存在着良好的正相关关系，为新型压实度监测系统提供了思路。