自锚式独塔悬索桥竖向弯曲振动基频估算公式
2019-05-14刘胜红蔡林真
郭 俊,刘胜红,高 嵩,蔡林真
(云南云路工程检测有限公司,云南 昆明 655600)
独塔自锚式悬索桥具有造型优美、观赏效果极佳等特点,是一种在城市市区或风景区等对景观要求较高地方具有竞争力的桥型。独塔自锚式悬索桥固有振动特性研究是分析该体系动力特性的基础[1-6]。
由于自锚式悬索桥是将主缆锚固在加劲梁上,此时加劲梁将承受较大轴向压力,故将导致其与地锚式悬索桥动力特性存在着较大差异[7-8]。王志诚[9]在考虑主塔刚度影响与否下,分别推导了带有外伸梁的双塔自锚式悬索桥竖向振动基频估算实用公式;张超等[10]采用Rayleigh法,在计入主塔刚度影响下,以三塔自锚式悬索桥为研究对象,推导了该体系竖向弯曲振动基频计算式;文献[11]所给出的振动基频估算式仅只针对地锚式悬索桥,而并未给出自锚式独塔悬索桥振动基频估算公式;王玉田等[12]以青岛海湾桥为研究对象,采用有限元分析对其开展了动力特性研究。
上述研究成果表明:学界对对称自锚式独塔悬索桥动力特性研究较少[13-14]。故笔者采用Rayleigh法,推导了竖向弯曲振动基频实用公式,可用于该体系桥梁在初步设计阶段选择合理的结构参数或校核有限元计算结果。
1 竖向弯曲频率计算
1.1 势 能
自锚式独塔悬索桥在铅垂平面竖弯振动时的势能分为主缆、加劲梁及主塔势能的总和。桥跨布置立面如图1。

图1 桥跨立面布置
主缆内力变化引起的弹性势能Uce如式(1):
(1)
式中:Ec、Ac分别为主缆的弹性模量及横截面面积;Hi为第i跨主缆水平分力增量;ls1、ls2分别为主缆虚拟长度;f1、f2分别为主缆垂度;θ1、θ2分别为主缆水平倾角。
主缆重力作用点引起的重力势能Ucg如式(2):
(2)
式中:Hq为成桥时刻主缆水平分力;v为加劲梁竖弯振动时振型函数。
加劲梁势能Ugs如式(3):
(3)
式中:Eg、Ig分别为加劲梁弹性模量和抗弯刚度。
加劲梁轴向压缩弹性势能Uge如式(4):
(4)
式中:Ag为加劲梁截面积。
主塔势能Ut如式(5):
(5)
式中:Sti为第i号主塔纵向单位抗弯刚度。
故自锚式独塔悬索桥在铅垂平面内振动时的总体势能U如式(6):
(6)
1.2 动 能
自锚式独塔悬索桥在铅垂平面竖弯振动时的动能为主缆、加劲梁、主塔及吊索动能总和。
主缆动能Tc如式(7):
(7)
式中:mc为主缆单位桥长质量。
加劲梁动能Ts如式(8):
(8)
式中:mg为加劲梁单位桥长质量。
主塔动能Tt如式(9):
(9)
式中:mti为第i号主塔质量;Ki为第i号主塔抗推刚度。
吊索动能为TH如式(10):
(10)
式中:mhi为第i号吊索质量。
故自锚式独塔悬索桥在铅垂平面内振动时的总体动能Tc如式(11):
(11)
1.3 频率计算
由能量法可得自锚式独塔悬索桥竖弯频率计算表达式如式(12):
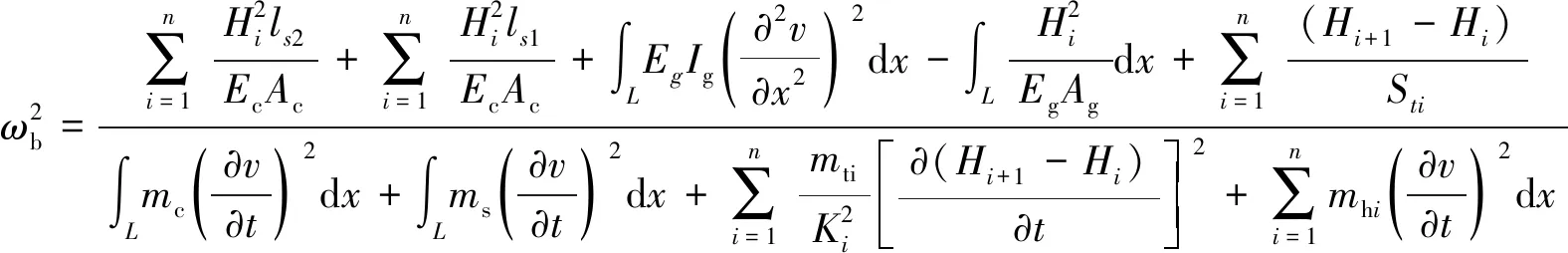
(12)
式(12)为独塔自锚式悬索桥竖弯基频能量表达式,需对其进一步简化。张超等[10]指出:在自锚式悬索桥体系势能中,主缆势能和加劲梁势能在该结构体系势能中占主导地位;该体系动能中,主缆和加劲梁动能在该体系动能中占主导地位,故式(12)可简化为式(13):

(13)
2 变形协调条件
自锚式独塔悬索桥一阶对称和反对称竖弯基本振型如图2。

图2 一阶对称和反对称竖弯基本振型
2.1 一阶对称竖弯基本振型及变形协调方程
图3为该体系在一阶对称竖向振动时的主塔受力情况。

图3 一阶对称主塔受力示意
由图3可知:主塔未发生纵向变形,即主塔两侧主缆水平增量之差为零,主塔受力平衡方程如式(14):
H1=H2
(14)
由变形协调条件,可得锚跨变形协调方程如式(15):
(15)
由式(14)、(15)可得式(16):
(16)
2.2 一阶反对称竖弯基本振型及变形协调方程
图4为该体系在一阶反对称竖向振动时的主塔受力情况。

图4 一阶反对称主塔受力示意
根据变形协调原理,可得锚跨及主跨变形协调方程分别如式(17)、(18):
(17)
(18)
主塔两侧主缆水平力增量与主塔变形相互平衡如图4,其受力平衡方程如式(19):
H1=H2+Stu
(19)
由式(17)~(19)可求得式(20):

(20)
3 一阶对称竖弯频率计算
加劲梁一阶对称振型如图2(a)。假设其外伸跨、锚跨和主跨加劲梁振型函数分别如式(21)~(23):
(21)
(22)
(23)
由加劲梁振型函数满足变形协调条件,则可得式(24):
(24)
由此可得式(25)~(27):
ls1)EcAc
(25)
(26)
(27)
将式(25)~(27)代入式(12),并简化可得其一阶对称基频估算表达式为式(28):
(28)
4 一阶反对称竖弯频率计算
加劲梁一阶反对称振型如图2(b)。设外伸跨、锚跨及主跨加劲梁振型函数分别如式(29)~(31):
(29)
(30)
(31)
由加劲梁振型函数满足变形协调条件,可得式(32):
(32)
由此可得式(33)~(35):
(33)
(34)
(35)
将式(33)~(35)代入式(12),并简化可得其一阶竖弯反对称基频的估算表达式如式(36):
(36)
5 算 例
某桥为自锚式独塔悬索桥,其跨径布置为(80+190+260+80)m,其计算参数与文献[12]一致。该桥计算参数及计算结果如表1、 2。

表1 计算参数
注:E为弹性模量;A为截面积;I为竖向抗弯惯性矩;Q为荷载集度。

表2 解析解与文献解计算结果比较
算例分析表明:由文中所推导的估算公式计算得到该体系竖弯基频与文献[12]之间存在一定差异,其中一阶对称竖弯之间的误差仅为5.61%,而一阶反对称竖弯的误差为11.52%。因此,一阶对称竖弯基频误差比一阶反对称基频误差要小,其原因在于该结构体系在做低阶反对称竖向振动时其实际振型为低阶反对称竖向振动与纵飘振动的耦合振动,而文中解没有计入耦合项,即该体系在做振动时仅仅视为竖向弯曲振动而忽略纵飘振动,从而使得一阶反对称竖弯振动与有限元解存在较大误差。
6 结 论
1)计算独塔自锚式悬索桥竖向弯曲振动基频时,其动力特性由主缆、加劲梁决定。
2)笔者采用能量法,推导了自锚式独塔悬索桥竖弯振动基频估算公式,可用于该体系桥梁初步设计阶段中结构参数的合理选择或校核有限元计算结果。
3)笔者所推导的竖弯振动基频估算实用公式仅适用于独塔自锚式悬索体系竖弯基频估算,而不适用于其他支承体系竖弯基频估算。为进一步提高所推导的估算公式计算精度,在后续研究中可计入纵飘振动对竖弯振动的影响,以提高文中推导的估算公式精度。
