柱状和球形颗粒在锥形布料盘表面的运动特性

bb

(常州大学a. 机械工程学院； b. 江苏省绿色过程装备重点实验室， 江苏常州213164)

颗粒是一种常见的物质形态，其特有的离散性使其表现出区别于一般的固体、液体和气体[1-3]。近年来，学者采用理论模拟、高速摄像和计算机视觉技术等揭示颗粒运动的规律[4]。其中Gui等[5]采用离散元法(DEM)对转鼓内四面体颗粒的混合与运动进行数值模拟，并将其与球形颗粒进行对比。李艳洁等[6]采用DEM模拟圆锥形贯入沙土的过程， 总结出不同贯入深度的料床速度场及力链分布规律。潘兵等[7]采用DEM分析了布料盘转速和颗粒直径对催化剂颗粒装填过程的影响。王志龙[8]采用CFD-DEM的研究方法得出循环流化床摆动到最大角位移处时颗粒的径向交换最明显。Ma等[9]采用CFD-DEM对离心复合力场中颗粒分离特性进行模拟。许晶等[10-11]采用CFD-DEM分析不同粒径球形颗粒的运动规律，并对比了单文丘里效应与双文丘里效应对粉体输送的影响，并用实验验证了模拟的准确性。上述研究结果表明，采用DEM方法能够有效模拟颗粒的运动行为，模拟结果得到了实验验证。

近年来，固体催化剂颗粒密相装填技术在过程工业中的应用快速增长，不同形式的颗粒布料盘是密相装填装置的核心单元。密相装填装置通过旋转运动布撒固体催化剂颗粒，使其均匀分布在反应器内部，形成密相催化剂床层[12]。由于颗粒形貌各异，布料盘表面结构不同，因此颗粒在布料盘表面的运动特性也会不同，进而会影响颗粒的布撒效果。目前对此问题的研究尚不多见。

本文中采用离散单元法描述高速、离散、随机颗粒的受力情况及运动规律，对颗粒在锥形布料盘表面的运动进行追踪分析，为通过改变布料盘结构参数与操作参数优化颗粒物料的布撒提供设计依据。

1 模型的建立及其参数设置

1.1 仿真模型

密相装填布料盘结构示意图及其仿真模型如图1所示。 如图1a所示， 为了研究开槽结构对颗粒运动的影响， 设计开槽前布料盘结构， 采用直径与高度比d∶h=1∶0.1的正锥形结构。 为了实现颗粒物料在床层上均匀分布， 必须使物料在旋转布料盘的不同半径处均匀抛出， 因此在布料盘上沿径向均匀开槽。 如图1b所示， 采用交错的环形条槽， 条槽宽度b=14 mm； 条槽的下边缘有防止颗粒快速甩出的翻边挡板。 如图1c所示， 为了便于模拟柱状及球形催化剂颗粒在布料盘上的运动过程， 在UG中按照1∶1建立布料盘模型， 并导入EDEM中， 建立仿真模型。

仿真模型主要由颗粒生成器和布料盘2个部分组成。为了降低颗粒在布料盘上的落点，减少颗粒初速度对运动特性的影响，将颗粒生成器设为直径仅为10 mm的圆形面，且距布料盘顶点10 mm。颗粒生成速度为1 000颗/s，共生成颗粒1 000颗。布料盘绕中心轴旋转，转速为n。

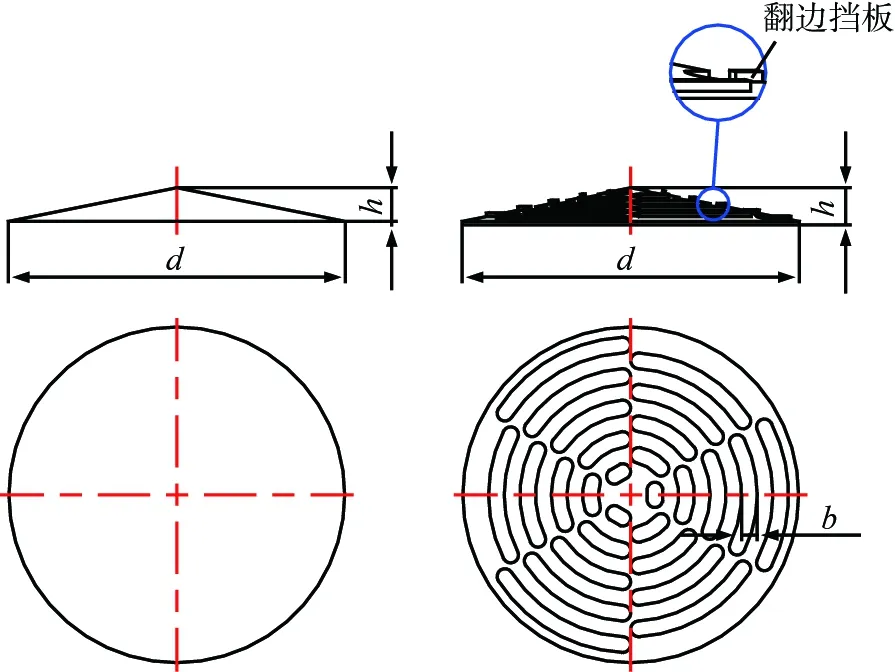
a 未开槽结构 b 环形条槽结构

c 仿真模型图1 密相装填布料盘结构示意图及其仿真模型Fig.1 Structure diagram and simulation model of dense loading distributor

颗粒选用加氢反应领域常用的柱状氧化铝催化剂，建立的催化剂颗粒模型如图2所示。其中，图2a为采用5颗直径为3 mm的小球叠合的柱状颗粒模型，其底面直径为3 mm，长度为9 mm。图2b所示为建立的球形颗粒模型，采用等体积球，当量直径为5 mm。

a 柱状颗粒 b 球形颗粒图2 催化剂颗粒模型Fig.2 Models of catalyst particles

1.2 数学模型

将颗粒设为离散相，每个颗粒的运动规律可由牛顿第二定律求解。在重力、离心力等复合力场中，颗粒可能与其相邻的颗粒或布料盘表面碰撞，从而交换动量。设定颗粒的运动有2种类型，即平动和转动，其任意时刻的运动方程[13-14]为

(1)

(2)

式中：分别为颗粒i的质量mi、转动惯量Ii、接触颗粒数ki、平动速度vi、转动速度ωi、颗粒i受到的流体阻力ffi、重力mig、接触力fcij、粘性接触阻尼fdij以及颗粒i与j之间的扭矩Tij。其中，fcij可以分为法向力fcnij和切向力fctij，fdij可以分为法向阻尼fdnij和切向阻尼fdtij。采用Hertz-Mindlin模型[15-17]，则有

(3)

fctij=-Stδt，

(4)

(5)

(6)

Tij=Rij×(fctij+fdtij)，

(7)

设E*为等效杨氏模量，R*为等效接触半径，Sn、St分别为法向和切向刚度，β为阻尼系数，m*为等效质量，其可由下列公式求出：

(8)

(9)

(10)

(11)

(12)

(13)

式中：G*为等效剪切模量，可由下列公式求出：

(14)

1.3 参数设置

DEM模拟过程中涉及的材料参数如表1所示，接触参数设置如表2所示。在该组参数下，分别模拟布料盘开槽前后柱状和球形颗粒在不同布料盘转速与直径下的运动过程。

表1 材料参数

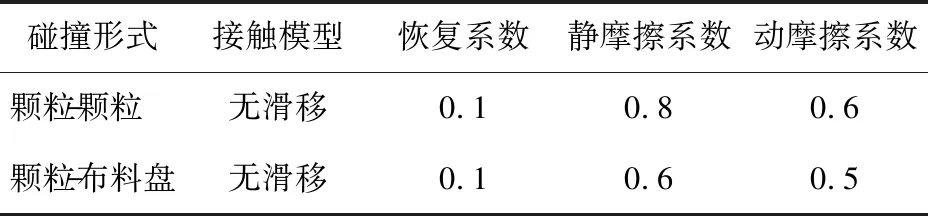
表2 接触参数

2 结果与讨论

2.1 在未开槽布料盘上的颗粒运动

2.1.1 颗粒运动过程分析

当颗粒与旋转布料盘面接触时，在重力、离心力、摩擦力和弹性力等的共同作用下，颗粒在布料盘面上作变加速运动，当布料盘直径为450 mm、转速为400 r/min时，颗粒在未开槽布料盘上的运动矢量图如图3所示。由图3可知，速度矢量自布料盘中心向边缘越来越长，可以判断颗粒速度逐渐增大；速度矢量箭头方向也在不断变化，且与布料盘的旋转方向一致并指向布料盘外，即颗粒在布料盘表面作离心运动。对比图3a、3b可知，柱状颗粒的速度矢量长度大于球形颗粒，这是由于球形颗粒受力更容易发生自身滚动，而不是随着布料盘作加速运动，从而球形颗粒速率小于柱状颗粒。

a 柱状颗粒 b 球形颗粒图3 颗粒在未开槽布料盘上的运动矢量图Fig.3 Vector diagram of movement of particles on the un-slotted distributor

球形颗粒和柱状颗粒各取5粒，以自颗粒生成器生成至甩出未开槽布料盘为期间，颗粒平均受力F随时间t的变化如图4所示。

图4 颗粒在未开槽布料盘上受力大小随时间的变化Fig.4 Variation with time of the force of particles on the un-slotted distributor

由图4可以看出，颗粒受力不均匀，大部分时间只受自身重力的作用，即不与布料盘和其他颗粒碰撞接触；偶尔受到瞬时的力，即与布料盘或其他颗粒碰撞接触，实现能量转换，且柱状颗粒受到的最大瞬时力为0.017 295 N，大于球形颗粒受到的最大瞬时力0.005 468 N；柱状颗粒停留时间少了0.02 s，因此柱状颗粒会更快地甩出布料盘。

各取1粒颗粒进行追踪，颗粒在未开槽布料盘面上的运动轨迹如图5所示。由图5可知，颗粒在未开槽布料盘上的运动轨迹在水平面上的投影近似一条对数螺旋线。

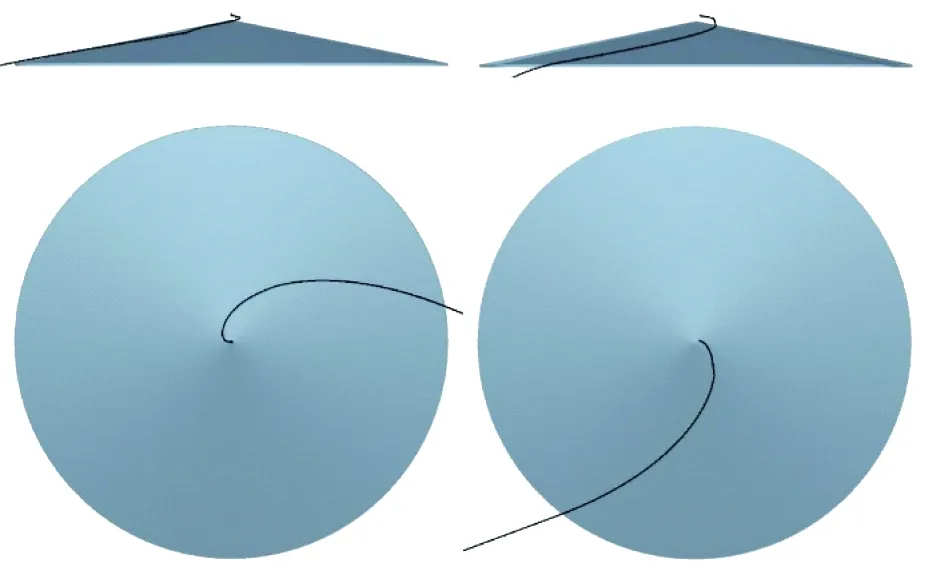
a 柱状颗粒 b 球形颗粒图5 颗粒在未开槽布料盘上运动轨迹Fig.5 Trajectory of particles on the un-slotted distributor

2.1.2 未开槽布料盘转速的影响

未开槽布料盘采用相同的直径d=300 mm，分别以100、150、200、250、300、350、400 r/min的转速对颗粒运动情况进行数值模拟。为了避免误差，选取20个颗粒，并导出它们刚甩出布料盘边缘的瞬时速率与竖直速率，进而计算得到平均水平速率vH和平均竖直速率vV。不同未开槽布料盘转速下颗粒的速度变化如图6所示，图6b中负号表示颗粒竖直速度方向向下。

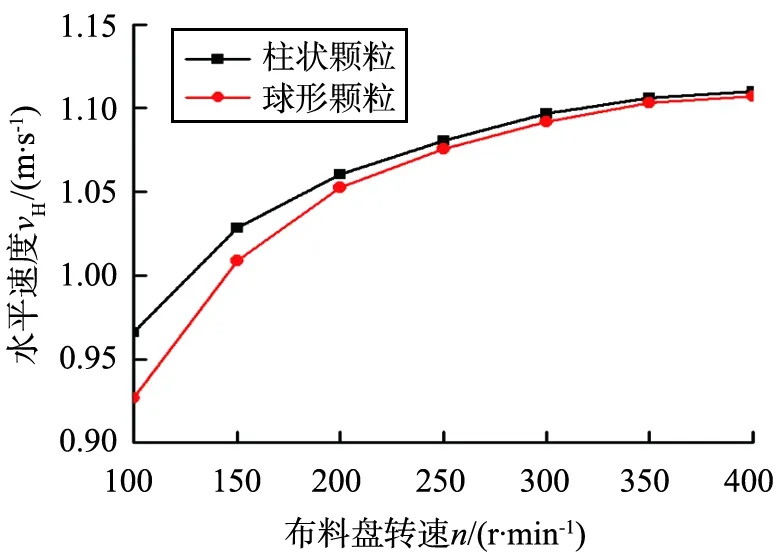
a 水平速度的变化

b 竖直速度的变化图6 不同未开槽布料盘转速下颗粒的速度变化Fig.6 Variation of particle velocity under different rotational speed of the un-slotted distributor

分析图6a、6b后可知，颗粒的水平、竖直速率随布料盘转速的增大而增大；由于布料盘直径较小，颗粒未能在布料盘上充分加速就已被甩出布料盘，且这种情况随布料盘转速的增大更加明显，因此速率的增幅逐渐变缓；柱状颗粒的水平、竖直速率都略大于球形颗粒；2种颗粒出盘速率的差值随布料盘转速的增加而逐渐减小，这表明随布料盘转速的增加，颗粒形状成为影响颗粒出盘速率的次要因素。同时，根据公式

(15)

进行计算，得到的布料盘边缘的线速度大于颗粒甩出盘时的水平速率，且两者差值随着转速的增大而进一步增大，与颗粒在水平旋转圆盘表面运动特性的研究结论一致[18]。

2.1.3 未开槽布料盘直径的影响

未开槽布料盘采用相同的转速n=400 r/min，分别对直径为300、350、400、450、500、550、600 mm的布料盘进行数值模拟。不同未开槽布料盘直径下颗粒的速度变化如图7所示，图7b中负号表示颗粒竖直速度方向向下。

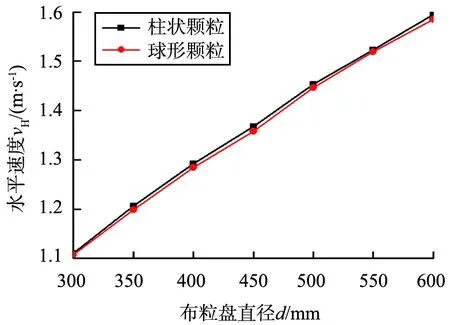
a 水平速度的变化

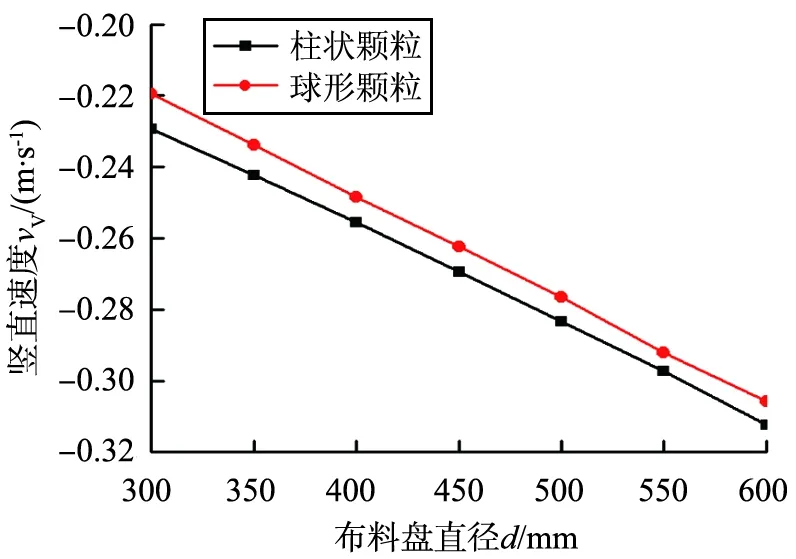
b 竖直速度的变化图7 不同未开槽布料盘直径下颗粒的速度变化Fig.7 Variation of particle velocity under different diameter of the un-slotted distributor

由图7a、7b可知，随着未开槽布料盘直径的增加，颗粒的水平、竖直速率呈一次线性增加，与布料盘边缘的线速度变化规律一致，但颗粒水平速率小于布料盘边缘线速度，且两者差值随布料盘直径的增大而增大。柱状颗粒与球形颗粒的出盘速率差异不大，这表明颗粒形状是影响颗粒出盘速率的次要因素。

2.2 在开槽布料盘上的颗粒运动

2.2.1 颗粒的运动过程分析

为了解决布料盘下方颗粒的装填问题， 实际用于催化剂装填的布料盘应在表面开槽。 为了防止颗粒快速离开布料盘， 下边缘采用翻边结构。 由于开槽以及翻边挡板的存在， 颗粒在开槽布料盘上的运动被干扰， 因此颗粒从各个条槽及布料盘边缘均匀抛出。 在开槽布料盘直径为450 mm、 转速为400 r/min的条件下， 颗粒在开槽布料盘上的运动矢量图如图8所示。

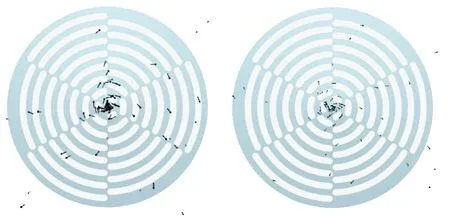
a 柱状颗粒 b 球形颗粒图8 颗粒在开槽布料盘上运动矢量图Fig.8 Vector diagram of movement of particles on the slotted distributor

由图8可知，与颗粒在未开槽布料盘表面的运动特性不同，部分颗粒因条槽及翻边挡板的影响而改变了运动方向。球形颗粒和柱状颗粒各取5粒，以自颗粒生成器生成至甩出开槽布料盘为期间，颗粒平均受力F随时间t的变化如图9所示。

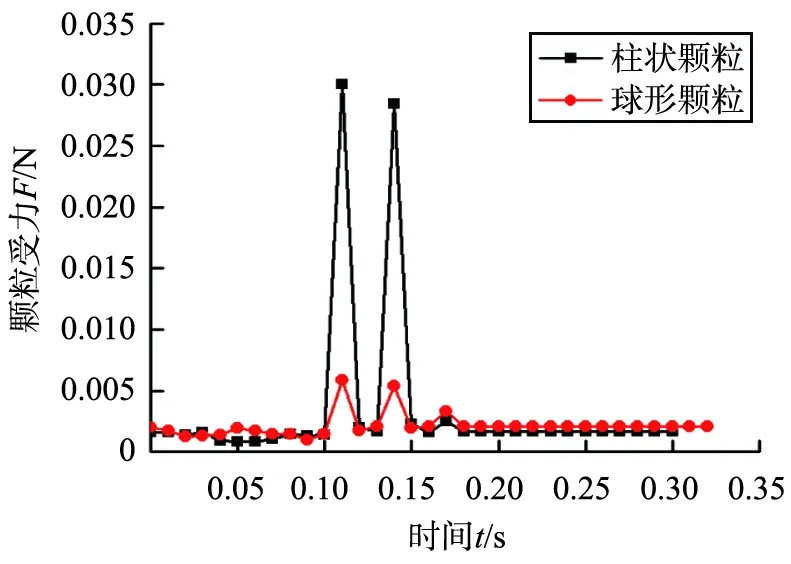
图9 颗粒在开槽布料盘上受力大小随时间的变化Fig.9 Variation with time of the force of particles on the slotted distributor

由图9可知，颗粒受力不均匀，会受到布料盘或其他颗粒施加的瞬时力；柱状颗粒受到的最大瞬时力为0.030 044 N，大于球形颗粒受到的最大瞬时力0.005 874 N；柱状颗粒比球形颗粒离开布料盘快出0.02 s，这一点与未开槽布料盘的情况相似；但由于开槽布料盘结构的变化使得颗粒受到的最大瞬时力更大，因此颗粒离开的时间比未开槽布料盘快0.09 s。

球形颗粒和柱状颗粒各取5粒颗粒进行追踪，颗粒在开槽布料盘面上的运动轨迹如图10所示。由图10可知，颗粒在开槽布料盘上的运动轨迹会出现弯折，甚至多次弯折。如图10a所示，柱状颗粒多数从靠近中心的条槽通过。如图10b所示，球形颗粒1、2从布料盘最内侧的条槽落下；颗粒3经过1次弯折，从布料盘中部的条槽落下；颗粒4经过2次弯折，通过靠近布料盘边缘的条槽；颗粒5经过2次弯折，没有通过条槽，而是从布料盘边缘抛出。

a 柱状颗粒 b 球形颗粒图10 颗粒在开槽布料盘上运动轨迹Fig.10 Trajectory of particles on the slotted distributor

2.2.2 开槽布料盘转速的影响

采用相同的开槽布料盘直径d=300 mm，分别对开槽布料盘转速为100、150、200、250、300、350、400 r/min时的颗粒运动情况进行数值模拟，设过槽率为通过条槽的颗粒占总颗粒的比率q，开槽布料盘不同转速下过槽率的变化如图11所示。

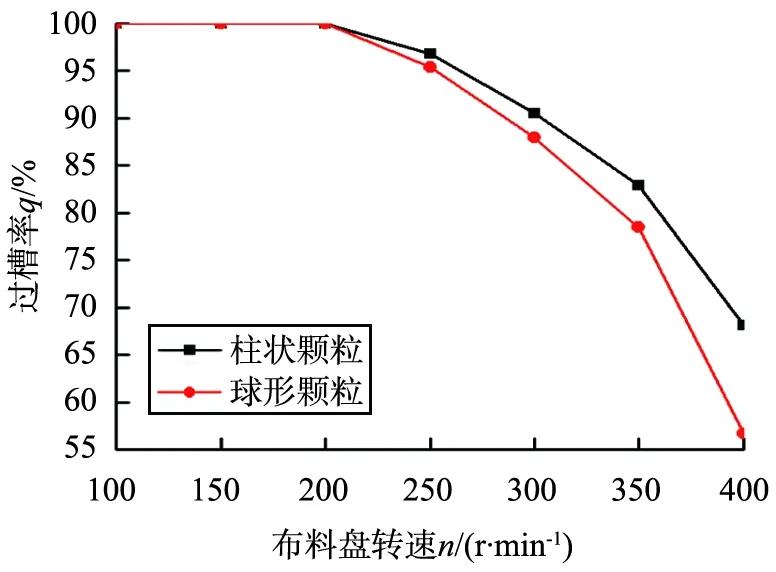
图11 不同开槽布料盘转速下过槽率的变化Fig.11 Variation of through-hole rate under different rotational speeds of the slotted distributor

由图11可知，当开槽布料盘转速≤200 r/min时，颗粒因条槽及翻边挡板的影响而加速不足，全部从条槽中通过布料盘；当转速>200 r/min时，颗粒受到了足以逃离布料盘的离心力而影响过槽率，过槽率随转速增加而下降，且下降的速度越来越快；同时，颗粒形状对过槽率有很大的影响，球形颗粒过槽率小于柱状颗粒，且两者差距随转速增加而逐渐增大，这是由于柱状颗粒在布料盘表面呈“平躺”状态，导致其重心距布料盘旋转轴小于球形颗粒。根据离心力公式

(16)

判断出球形颗粒受到的离心力更大，且随着转速的增大，2种颗粒受到的离心力差异逐渐增大，从而球形颗粒更易甩出开槽布料盘边缘。

对开槽布料盘转速≥250 r/min时颗粒的水平、竖直速率进行分析，不同未开槽布料盘转速下颗粒的速度变化如图12所示。

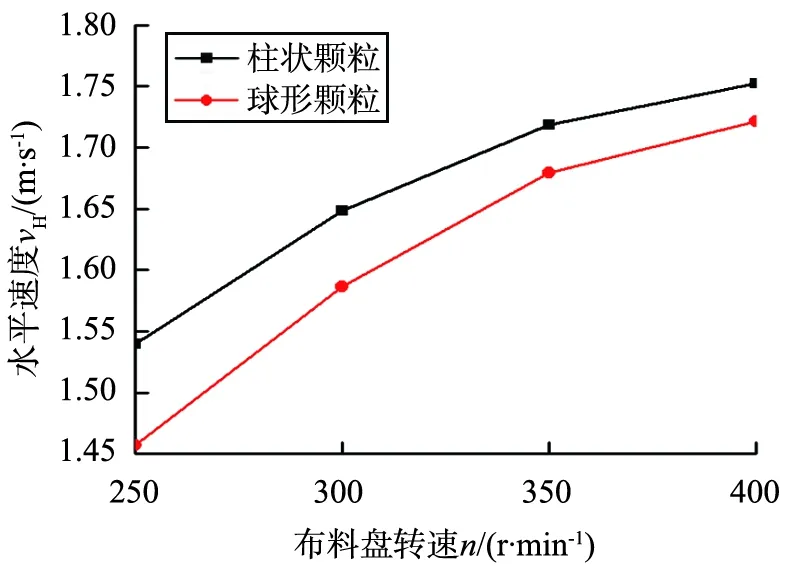
a 水平速度的变化

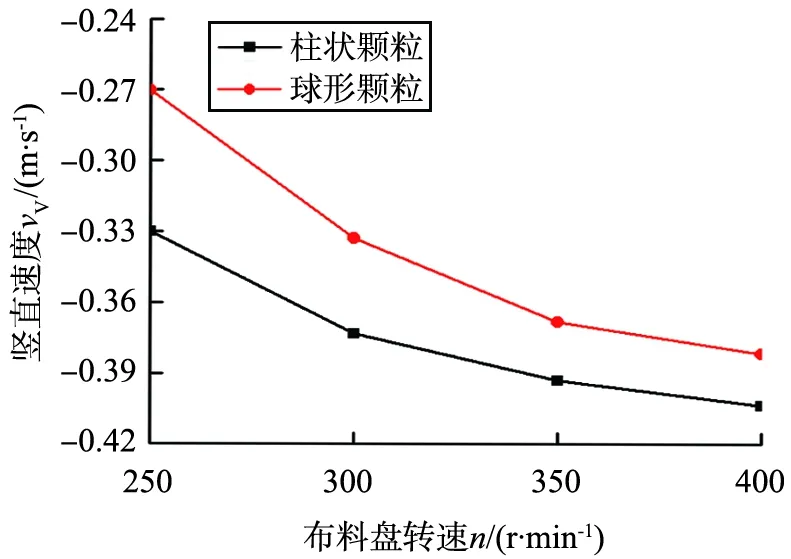
b 竖直速度的变化图12 不同开槽布料盘转速下颗粒的速度变化Fig.12 Variation of particle velocity under different rotational speeds of the slotted distributor

与未开槽锥形布料盘相似，颗粒的水平、竖直速率随开槽布料盘转速的增大而增大，且增大的幅度逐渐减小；柱状颗粒的水平、竖直速率略大于球形颗粒。开槽后颗粒的水平、竖直速率都略大于未开槽时的情况，这是由于颗粒受到翻边挡板的力更大。

2.2.3 开槽布料盘直径的影响

为了更好地研究过槽率的变化，开槽布料盘采用相同的转速n=400 r/min，并对直径为300、350、400、450、500、550、600 mm的开槽布料盘进行数值模拟。不同开槽布料盘直径下过槽率的变化如图13所示。

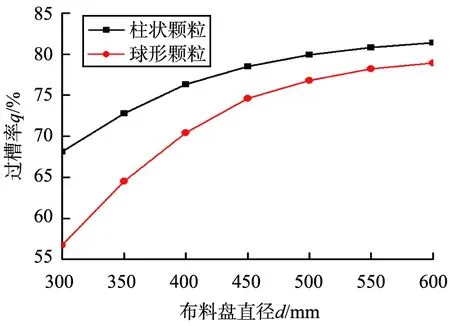
图13 不同开槽布料盘直径下过槽率的变化Fig.13 Variation of through-hole rate under different diameters of the slotted distributor

由图13可知，颗粒的过槽率随开槽布料盘直径的增大而增大，且增幅逐渐减小。这是由于随着开槽布料盘直径的增加，布料盘的条槽数也增加，从而增加了颗粒通过条槽的概率，但甩出开槽布料盘边缘的颗粒与布料盘成非接触状态，因此开槽布料盘直径的增加对过槽率提升有限；柱状颗粒的过槽率大于球形颗粒，且两者之间的差距随开槽布料盘直径的增大而减小；根据离心力公式，2种颗粒受到的离心力有一定的差值，布料盘直径的变化不影响离心力差值的变化，但直径的增大带来了边缘颗粒受到的离心力的增大，因而此差值占离心力比例减小。

3 结论

采用离散元法对柱状、球形颗粒在正锥形布料盘表面的运动过程进行数值模拟，比较了布料盘开槽前后不同的布料盘转速、直径以及颗粒形状对运动过程的影响。通过分析颗粒在布料盘上的运动规律，得出以下结论：

1)颗粒在旋转布料盘表面作离心运动，速率由中心向边缘逐渐增大。

2)颗粒在布料盘表面的受力不均匀。柱状颗粒受到的最大瞬时力大于球形颗粒，提前0.02 s甩出布料盘；布料盘开槽后颗粒受到的最大瞬时力大大增加，进而能更快地抛出布料盘。

3)开槽前颗粒在布料盘表面的运动轨迹近似对数螺旋线，开槽后颗粒的运动轨迹会发生弯折，从而均匀地通过布料盘不同半径处的条槽。

4)颗粒出盘的水平、竖直速率随布料盘转速、直径的增大而增大；柱状颗粒出盘的水平、竖直速率略大于球形颗粒；开槽后颗粒出盘的水平、竖直速率大于开槽前。

5)开槽后颗粒的过槽率随布料盘转速的增大而减小，随布料盘直径的增大而增大，且柱状颗粒的过槽率大于球形颗粒。