基于滑移凸轮机构的累积误差分布计算

楼狄明1 张卓群

(1. 同济大学, 上海 210000；2. 上海汽车集团股份有限公司技术中心, 上海 210000)

1 研究背景

在机械零件与总成的设计过程中，会经常进行关键尺寸的校核与计算。通常关键尺寸是由数个甚至更多的图纸标注尺寸累积而成。传统的极值法计算累计误差结果偏差范围较大。在对关键尺寸要求严苛的情况下，会反过来加严图纸标注尺寸的公差，增加零件加工和总成装配的难度。

滑移凸轮机构是一种复杂机械结构，对传统发动机而言，一般只具有一个固定的气门升程，无法满足发动机多变的转速与负荷，气门升程曲线设计往往需要兼顾各种工况。但滑移凸轮机构使发动机具有2个气门升程，与运行工况的匹配度更高，能够提高发动机性能。在油耗及排放法规越来越严苛，消费者对发动机性能的要求越来越多样化的情况下，滑移凸轮机构能起到对应的作用，在发动机上的应用也会越来越广泛。

本文在介绍滑移凸轮机构的基础上，针对其关键尺寸进行均方根法累计误差计算和误差分布分析，缩小偏差并将其期望范围控制在非常高的分布概率，降低零件加工和总成装配难度。

1.1 滑移凸轮机构相比其他解决方案的优缺点

为使气门升程能够可变，国内外提出了可以实现可变气门升程的多种技术路线。从功能的角度可以分为连续可变气门升程和两级可变气门升程。

本田公司的可变气门正时和气门升程电子控制(VTEC)技术通过主摇臂、中间摇臂和辅助摇臂的设计，由电磁阀控制液压，达到气门升程可变的目的[1]。Rodolf Flierl等[2]提出的“Univalve”是一种机械式的全可变气门传动系统，它能够使气门升程在0和最大升程之间任意变化。 伊顿公司和通用汽车公司采用了一种两级可变气门升程机构(DVVL),该结构的摇臂分为外摇臂和内摇臂，相应的凸轮位置设计为外侧的2个高升程凸轮和内部的1个低升程凸轮组成[3]。菲亚特公司的Multiair系统在无凸轮轴的情况下实现了气门升程无级可调，进气门由活塞、液压腔和电磁阀完成驱动[4]。Dojoong Kim等[5]开发了一种两级可变气门升程机构，且带有电子控制阀，研究了此种结构在1个发动机工作循环内的切换性能。Thitiphol Anontaphan[6]针对一款连续可变摇臂结构进行了研究，说明其优缺点并预估了对发动机油耗的影响。

综上所述，以上机构均具有结构复杂、成本高等特点，所以工程应用的案例不多，相比整体市场的规模更是微乎其微。

滑移凸轮式两级可变气门升程目前仅在部分汽车公司的海外车型有工程应用案例，国产车型并无应用，其具有结构相对简单、切换迅速、对原气门机构影响小、成本较低等优点。

1.2 滑移凸轮机构

常见的滑移凸轮机构主要包括1个滑移式凸轮轴总成和若干个电磁阀。图1示出了1个已经进行了工程应用的滑移式凸轮轴总成。

图1 某滑移凸轮结构示意图

2 关键尺寸解析

要解析滑移凸轮机构的关键尺寸，首先要确认滑移凸轮机构要实现的功能，确保在整个系统中实现主要功能的尺寸是关键尺寸。

另外，在保证滑移凸轮机构功能实现的同时，仍要考虑整个系统的潜在失效模式，以确定其他关键尺寸。

2.1 机构主要功能

整个系统的首要功能是保证凸轮套沿着花键轴按照设计的轨迹进行滑移，而滑移的关键之一就在于切换销与沟槽的正常接触，使其在设计位置能够顺利深入切换沟槽且不发生干涉，又要避免切换销与沟槽侧边之间间隙过大，防止切换销直接与沟槽侧边的切换段中间部分接触，从而产生较大的初始速度和加速度。由此可见，切换销与沟槽侧边的初始设计间隙显得尤为重要。

整个系统的第二个功能是能够保证滑移凸轮套在高低气门升程两个稳态时的可靠性，使其在止推功能的作用下不沿花键轴轴向进行移动。按上文所述，凸轮套的止推除轴承档侧面外，还需要弹簧和钢球的组合来与钢球槽斜面接触产生侧向力，起到辅助止推的作用。

而与此同时，钢球槽斜面的大小又受到花键尺寸参数与凸轮套外圆尺寸的双重影响，其内边不能超出花键齿顶尺寸，外边又要与切换沟槽底部保持一定壁厚以保证结构强度。为了解决这个矛盾，需要在斜面与内孔和斜面与斜面交界处设计一定的圆角，其目的在于一方面减小凸轮套滑移时钢球与钢球槽的摩擦力，另一方面方便钢球槽机械加工。可见，钢球与斜面接触点在制造偏差的影响下产生的偏移会对斜面大小产生挑战，所以需要对接触点的偏移情况进行尺寸分析，以保证接触点在正确的位置，同时可以为动力学研究提供理论支撑。

2.2 机构潜在失效模式

潜在失效模式为凸轮不能在厚度方向上包容摇臂滚轮。按照设计经验可知，凸轮一般必须在厚度方向上包容摇臂滚轮，否则可能会产生一定的侧向力，对整个气门传动机构的工作可靠性以及振动-噪声-平顺性(NVH)都会造成不良的影响。而滑移凸轮机构受轴向空间的限制，滑移行程不能过大，同时在原来布置1个凸轮的位置设计2个高低升程凸轮，这样凸轮厚度就会很小，而从动力学的角度摇臂滚轮厚度不能太小，否则与凸轮之间的接触强度可能超出材料的许用应力值。

一般滑移凸轮机构的凸轮厚度仅比摇臂滚轮厚度大1.0～1.5 mm，在制造误差的影响下摇臂滚轮在厚度方向上很可能超出凸轮的包覆范围，产生侧向力，造成不良影响甚至失效。所以凸轮与摇臂滚轮在厚度方向上的尺寸链分析和公差分布计算非常重要。

3 尺寸链校核和误差分布计算

3.1 凸轮与滚轮配合

针对前文所述的潜在失效模式进行校核，运用极值法最终分析出凸轮前后边界到摇臂滚轮边界的距离，以判断在制造误差的影响下，摇臂滚轮在宽度上是否超出了凸轮的包覆范围，如表1和表2所示。

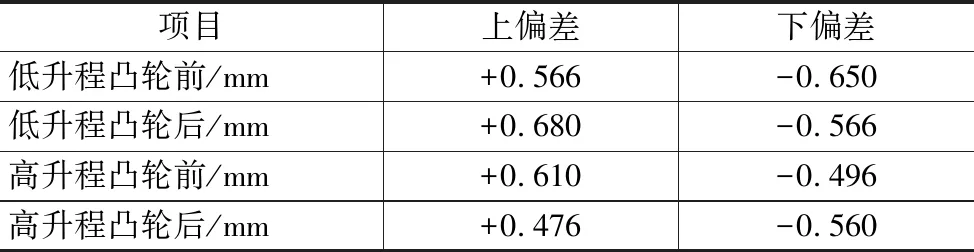
表1 1号摇臂极值法校核结果

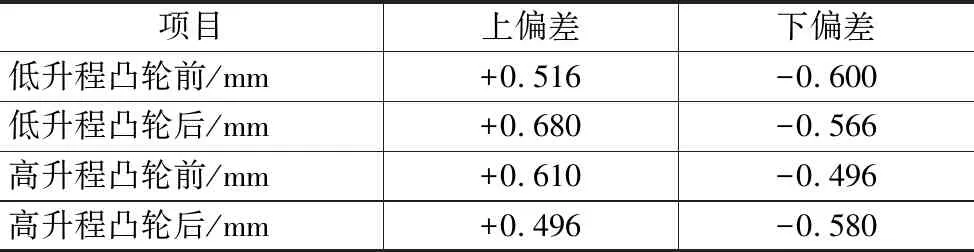
表2 2号摇臂极值法校核结果

根据计算结果判断，所计算的尺寸极值均大于0，符合一般需求，但同时存在个别情况偏差过大，极值已经接近0，存在一定的风险，不符合设计准则，需要加严各个标注尺寸的公差标注，增加加工难度。

按照均方根法校核凸轮与摇臂滚轮在宽度方向的包覆情况，并与极值法校核结果对比。假设所有的尺寸都遵循正态分布，且所有公差体现的都是相同的标准差数量，尺寸链尺寸都为对称公差。

以1号摇臂滚轮与低升程凸轮前端的距离为例，其尺寸链尺寸数为12个，对称的上下偏差分别为±0.04 mm、±0.006 mm、±0.003 mm、±0.1 mm、±0.002 5 mm、±0.003 mm、±0.05 mm、±0.037 5 mm、±0.2 mm、±0.1 mm、±0.03 mm和±0.04 mm。

计算得出1号摇臂滚轮与低升程凸轮前端的校核偏差为Tasm=0.261 mm，其他校核位置的计算结果如表3所示。

表3 均方根法校核结果

从表3可以看出，均方根法的计算结果累积误差要远小于极值法，校核理论值均大于0且存在一定安全余量。

接下来进行误差分布计算。在正态分布函数计算中的NORMDIST是指返回指定平均值和标准偏差的正态分布函数。此函数在统计方面应用范围广泛(包括假设检验)。能建立起一定数据频率分布直方与该数据平均值和标准差所确定的正态分布数据的对照关系。

根据图2所示的6-Sigma理论，均方根法计算所得Tasm为3σ，σ即为分布的标准方差(正数)。算术平均分布值为0.667 mm。

图2 6-Sigma原则示意图

区间点X设定在保证摇臂滚轮不超出凸轮的包覆范围，且必须大于0。考虑到其他因素的影响且预留一定的安全系数，初设此点为0.3 mm。表4为使用累计分布函数“TURE”的参数值。

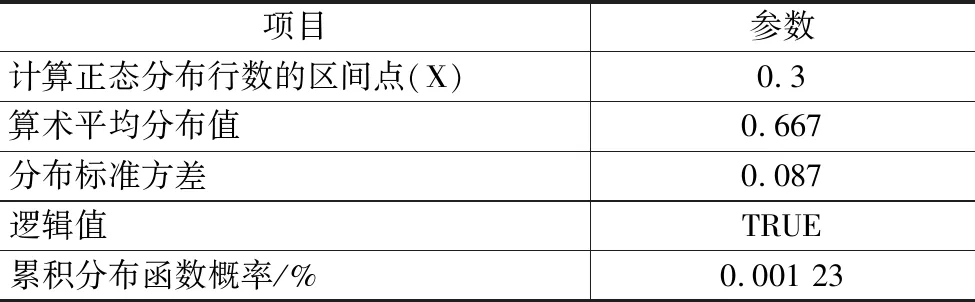
表4 使用累计分布函数TRUE参数值

由表3可知，计算距离值小于0.3的概率为0.001 23%，相当于10万台发动机中有1台存在安全风险，符合工程要求。

综上所述，均方根法比极值法有很大优势，不仅可以缩小偏差范围，还可以进行任意区间的分布概率计算。

3.2 切换销与螺旋槽侧面间隙尺寸分析

如前所列尺寸，针对切换销与切换侧边之间的间隙进行了尺寸链计算。

共涉及两个切换销前后两侧共4个间隙值(除切换侧边一侧外，还需计算槽另一侧以避免干涉)。表5示出了切换销两侧采用间隙极值法结果。表6示出了切换销两侧间隙采用均方根法校核结果。

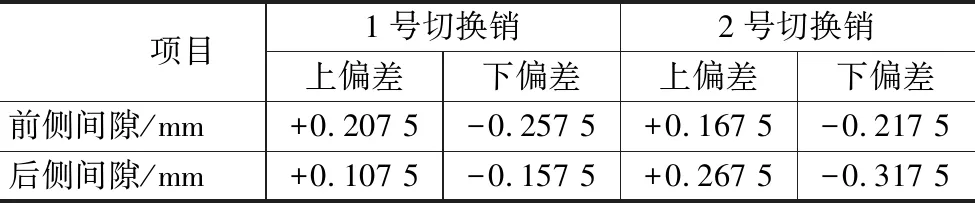
表5 切换销两侧间隙极值法校核结果

从结果可知，在切换销与切换侧边的关键间隙处，按照极值法计算仍保持有较大的最小间隙。

间隙的设计原则为最小间隙值能够保证切换销与侧边接触时不会相互干涉，并预留一定的安全间隙，最大间隙值一定要在切换侧边型线设计的缓冲范围内。

以2号切换销前侧间隙为例，进行误差分布计算得出：Tasm=0.082 6 mm，分布标准方差为 0.027 5 mm。

表6 切换销两侧间隙均方根法校核结果

按照设计经验，精密运动件可考虑保持0.2 mm的最小间隙值。若将名义间隙值减小为0.3 mm，公差不变，则误差分布计算结果为：间隙小于0.2 mm的概率为0.000 002 45%，间隙大于0.5 mm的概率数值一样。可见，间隙值基本落在0.2～0.5 mm范围内。

减小间隙能够避免较大的初始瞬时接触应力，提高系统的可靠性和NVH性能等。均方根法计算可以在有充足依据的情况下减小间隙，相比极值法计算有一定优势。

另外值得注意的是，所进行计算的间隙值与切换销和侧边的实际接触点并不是同一概念，因在切换销的实际工作中，因切换侧边是带有斜度的，随着凸轮轴的旋转，实际接触点并不是切换销最靠近平面侧面的某条线，而是最靠近斜面的某条线，其切换侧边型线设计零点的距离要比误差分布计算理论值要大。

4 总结与展望

通过均方根法计算累计误差和基于其结果的误差分布概率计算对于工程应用有很大的帮助，能够减小极值法计算的误差分布区间，在一定意义上更加精确，且利用概率法指导生产过程，判断目标值偏出期望区间的可能性。

同时，在应对类似滑移凸轮机构这种复杂机械结构设计的情况下，结合均方根法进行设计校核是一种准确和可靠的手段，可以预见在未来的复杂机构计算中会更多的采用概率法来应对复杂尺寸链。