基于正交试验的压缩式封隔器胶筒的结构参数优化

2019-05-13祝效华许建波

天然气工业 2019年3期

张智祝效华许建波

1.成都中腾石油工程技术有限公司 2.西南石油大学机电工程学院3.中石化胜利石油工程有限公司井下作业公司

0 引言

封隔器胶筒是封隔器最为重要的核心组成部件之一，其作用主要是封隔油管与套管环形空间，达到隔绝产层、保护套管的目的[1]。现场使用中，封隔器胶筒密封失效和撕裂失效问题较为突出，已成为当前关注的焦点问题之一。

为了解决上述问题，国内外学者对封隔器胶筒做了相关研究，已有的封隔器胶筒力学模型和数值计算方法[2-3]，对其力学性能评价较为准确、合理。Polonsky和Tyurin等[4]将封隔器圆柱形胶筒设计为圆锥形，同时使用软硬胶筒相组合的胶筒组和弹簧环防突装置，提高了封隔器的密封性能；Hu Gang等[5]通过实验获得了3种橡胶的材料本构关系，采用有限元法分析了不同材料对封隔器胶筒力学性能的影响；Ma Weiguo等[6]采用有限元法研究了摩擦系数对封隔器胶筒接触应力的影响；仝少凯[7]采用理论计算分析了压缩式封隔器胶筒的力学性能，指出封隔器胶筒的接触应力随着轴向载荷的增加而增加，随着胶筒橡胶材料剪切模量的增加而减小；于桂杰等[8]利用ANSYS 软件建立了封隔器异型胶筒有限元模型，对比分析了常规胶筒和异型胶筒的密封性能以及圆槽半径对封隔器密封性能的影响。上述研究主要集中于封隔器胶筒力学性能分析，也有涉及结构改进部分，但目前在封隔器上使用最多的胶筒依然是常规胶筒。由此可见，针对封隔器常规胶筒进行参数优化，从而提高其密封性能和使用寿命具有重要意义。

针对上述问题，笔者首先依据虚功原理、Von Mises屈服准则以及接触非线性理论，构建了封隔器胶筒的三维有限元计算模型；进而对胶筒结构的关键参数采用正交优化方法[9]进行优化，获得了胶筒结构的关键参数最优组合。

1 胶筒材料本构模型及参数

橡胶材料存在多种本构模型，其中Mooney-Rivlin模型是一种常用的本构模型，它几乎适用于橡胶材料的所有力学行为模拟[10]。因此，笔者采用具有较好拟合橡胶材料中等变形的Mooney-Rivlin模型，该模型模拟胶筒在外力作用下变形的应变能密度函数W为[11]：

式中I1、I2表示变形张量不变量；C10、C01表示Rivlin系数。

Mooney-Rivlin模型中的C10、C01可以通过单轴拉伸试验、双轴拉伸试验、平面剪切试验的实验数据获得，也可以通过经验公式确定。据研究表明，橡胶硬度（Hr）与弹性模量（E0）之间的关系可以表达为[12]：

采用两参数Mooney-Rivlin 模型作为胶筒本构模型，由于橡胶为不可压缩材料，其Rivlin系数与弹性模量关系[13]为：

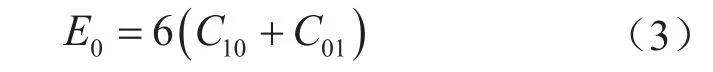
根据经验，C01和C10的比值范围一般为0.25～0.5[14]，笔者计算中取0.5，橡胶材料硬度取90IRHD，从而利用式（2）、（3）计算得到该橡胶材料的弹性模量为17.33 MPa，C10、C01分别为1.926和0.963。本文选取的常规压缩式封隔器（以下简称封隔器）参数尺寸如表1所示。

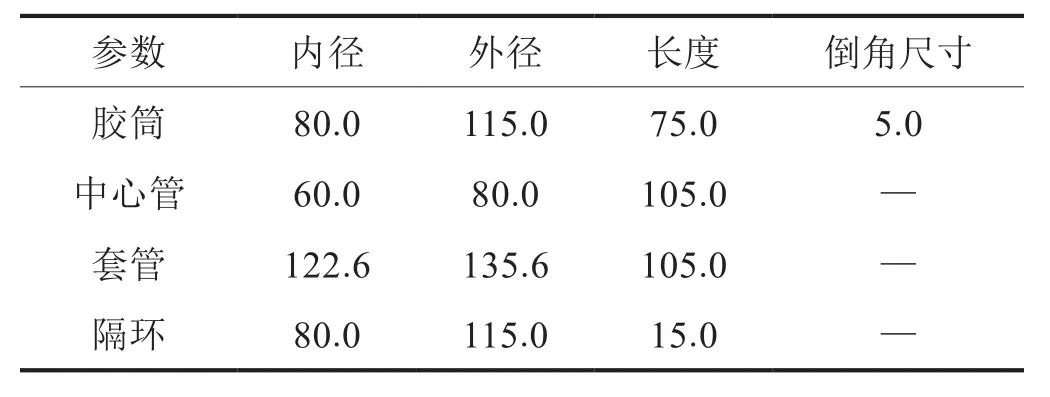
表1 压缩式封隔器参数尺寸表 mm

2 封隔器胶筒有限元计算模型

2.1 封隔器胶筒有限单元模型及边界条件

以表1中数据对应的封隔器为研究对象，胶筒材料为丁晴橡胶，其密度为1.20 g/cm3，Rivlin系数C10、C01分别为1.926和0.963；套管、中心管以及隔环均为合金钢，其密度为7.85 g/cm3，弹性模量为2.07×105MPa，泊松比为0.28。封隔器胶筒有限元计算模型采用了有限元三维分析评价技术，计算中考虑了润滑作用的影响，所有接触面的摩擦系数均取0.3[15]。

模型假设：①将胶筒、套管、中心管、隔环均视为各向同性、连续的均质体；②不考虑硬化和蠕变带来的影响；③胶筒材料视为体积不可压缩材料。采用C3D8R六面体单元对模型进行网格划分，共划分网格单元31 760个，其中胶筒8 320个，套管8 400个，中心管11 200个，隔环3 840个，网格单元模型及边界条件如图1所示。

模型边界条件：在套管、中心管以及下端隔环2的下表面施加固支边界，消除自由度；在上端隔环1的上表面施加坐封载荷。采用罚函数法定义库伦摩擦形式的切向接触条件，法向接触条件设为硬接触，采用通用接触对进行接触控制。考虑坐封过程中胶筒与套管、中心管之间的接触非线性，计算中将几何非线性开关打开。

图1 封隔器网格单元模型及边界条件图

2.2 有限元计算模型验证

为了验证本文有限元计算模型的精确性，首先建立了与本文参考文献[16]规格相同的封隔器边胶筒的有限元计算模型，研究了实验工况（坐封载荷1.66 MPa、3.3 MPa、5 MPa、6.68 MPa、8.36 MPa 及10.03 MPa）下边胶筒的压缩距，模拟结果与实验结果对比如图2所示。

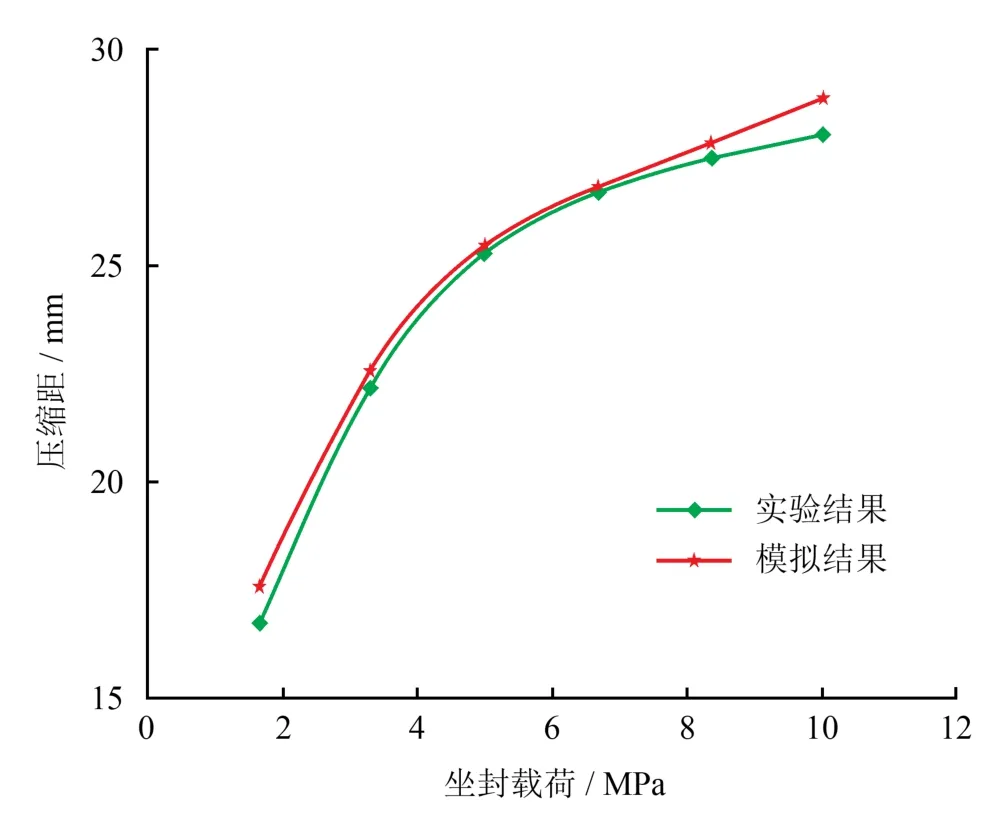
图2 模拟结果与实验结果对比图

从图2中可以看出，两种方法测得的压缩距结果基本相同，总体数值差异小，整体上吻合性较好。模拟结果与实验结果对比，两者之间的最大误差仅为4.96%，而本文参考文献[16]采用二维轴对称模型计算的结果误差达到9.26%，说明三维模型更符合实际，计算精度更高，其对二维模型进行了修正，进而验证了本文所建立的封隔器胶筒三维有限元计算模型具有较高的计算精度。

3 封隔器胶筒的结构参数正交优化

3.1 正交优化因素

针对常规压缩式封隔器胶筒易发生密封失效和使用寿命短的问题，以提高胶筒密封性为目的，以不降低胶筒使用寿命为原则，基于常规压缩式封隔器胶筒计算模型，对胶筒结构关键参数：长度、厚度、倒角尺寸进行正交优化，获得最优参数组合，各参数取值如表2所示。

表2 正交优化因素水平表 mm

3.2 正交优化试验方案及结果分析

为了获得性能较优的封隔器胶筒参数的最优组合，在坐封载荷20 MPa作用下，计算了9种胶筒结构的关键参数组合下胶筒与套管间的接触应力。将计算结果作极差（极差又称范围误差或全距）评价。极差反映了试验指标随因素水平波动时的变动幅度，从而分析得到最优参数组合，正交优化试验方案及结果如表3所示。

表3给出了坐封载荷20 MPa作用下的正交优化试验方案及计算结果。从表3中可以看出，不同因素下的接触应力结果极差不同，计算的长度、厚度、倒角尺寸等3个因素的极差分别为0.91、4.99、0.95，由极差大小可以确定出长度、厚度、倒角尺寸这3个因素对封隔器胶筒接触应力影响的主次顺序，其主次顺序依次为：厚度＞倒角尺寸＞长度。由此可见，在研究范围内，封隔器胶筒参数的优组合为A3B3C3，即厚度20 mm、倒角尺寸10 mm、长度80 mm。

4 优化前后封隔器胶筒力学性能对比

为了进一步说明优化后的封隔器胶筒在应用中的优势，采用有限元法计算了优化后（胶筒参数A3B3C3）与优化前（胶筒参数见表1）两种结构分别在坐封载荷10 MPa、12.5 MPa、15 MPa、17.5 MPa以及20 MPa作用下胶筒的压缩距、Mises应力以及胶筒与套管间的接触应力，比较两种结构的密封性能和使用寿命，结果如图3、4、5所示。

表3 正交优化试验方案及结果表

图3 优化前后胶筒压缩距对比图

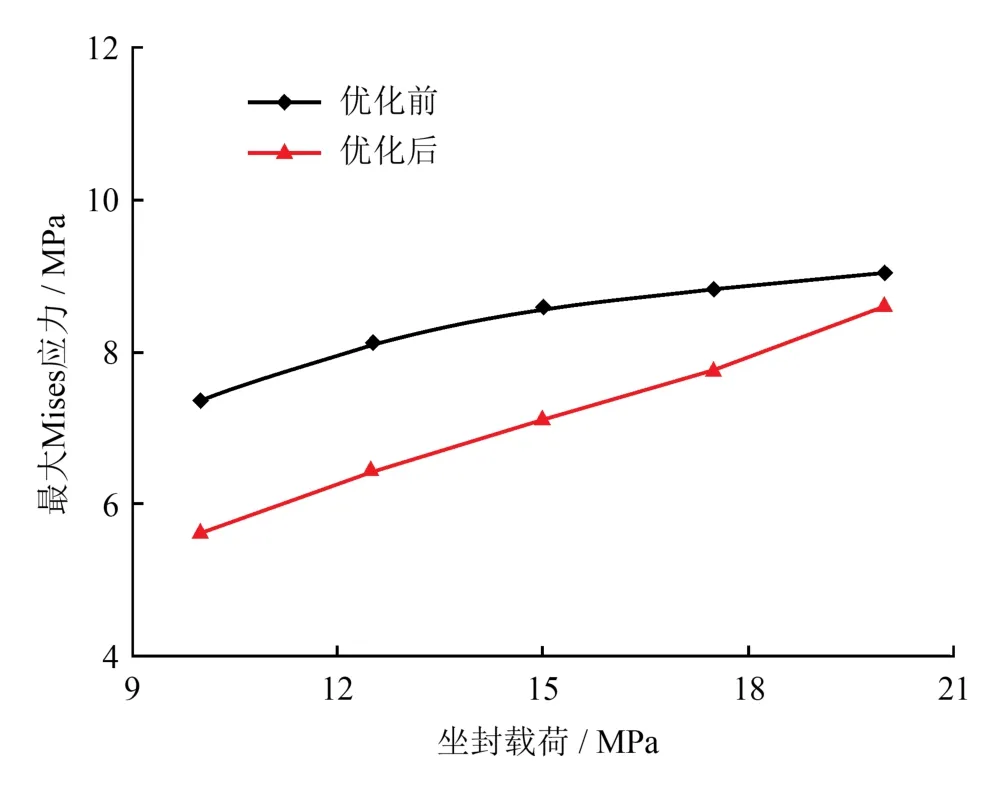
图4 优化前后胶筒最大Mises应力对比图

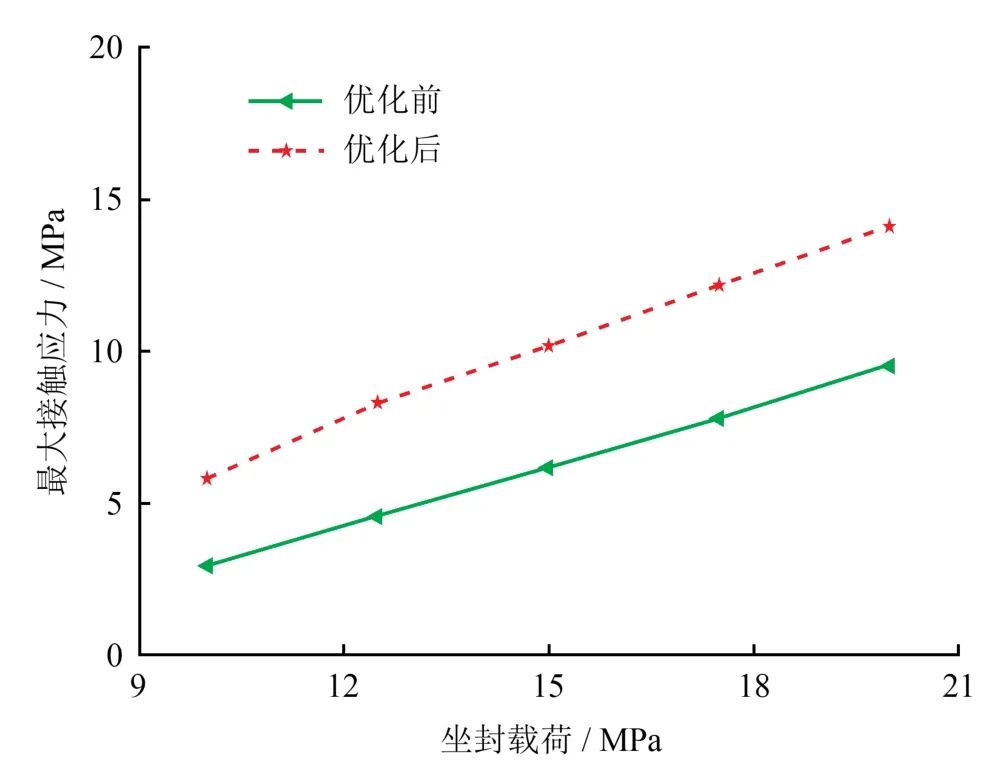
图5 优化前后胶筒与套管间最大接触应力对比图

图3给出了不同坐封载荷下优化前后胶筒的压缩距。从图3中可以看出，随着坐封载荷的增大，优化前后胶筒压缩距增大。在相同坐封载荷下，优化后胶筒的压缩距小于优化前胶筒的压缩距。在上述5种坐封载荷下，优化后胶筒的平均压缩距降低37.82%。由此可见，在相同坐封载荷下，优化后的胶筒变形形态更小，其与套管的接触长度更长，密封性更好。

图4给出了不同坐封载荷下优化前后胶筒的最大Mises应力。从图4中可以看出，随着坐封载荷的增大，优化前后胶筒的最大Mises应力均增大，坐封载荷的增大将增大胶筒强度失效的风险。在相同坐封载荷下，优化后胶筒的最大Mises应力小于优化前胶筒的最大Mises应力。在上述5种坐封载荷下，优化后胶筒的最大Mises应力平均降低15.72%。由此可见，在相同载荷工况下，优化后胶筒的使用寿命更长。

图5给出了不同坐封载荷下优化前后胶筒与套管间的最大接触应力。从图5中可以看出，随着坐封载荷的增大，优化前后胶筒与套管间的最大接触应力均增大，说明坐封载荷越大，胶筒与套管间的密封性越好；在相同坐封载荷下，优化后胶筒与套管间的最大接触应力大于优化前胶筒与套管间的最大接触应力；在上述5种坐封载荷下，优化后胶筒与套管间的最大接触应力平均增大70.44%。由此可见，在相同载荷工况下，优化胶筒与套管间的密封性更好。