天然气储层含气性定量评价新参数

2019-05-13王修朝

天然气工业 2019年3期

王修朝

中国石油集团长城钻探工程有限公司地质研究院

0 引言

天然气储层的产能评价是储层测井综合解释的重要环节，同时也是难点所在[1-5]。近年来，随着致密气、页岩气等复杂含气储层勘探程度的不断加大，含气性解释评价的要求不断增加[6-14]，难度也日益凸显，主要表现在岩石物理实验测量过程困难、低孔低渗对含水饱和度计算精度的影响大、孔隙结构对储层导电机理的控制作用复杂等方面。同时，由于天然气的物理性质特殊，气态烃类在地下的赋存受到温度、压力、地层水、岩石性质等多方面因素的影响，基于体积百分比的饱和度评价参数已不能完全反映储层的产气能力，提出一套精确的天然气产能评价方法迫在眉睫。为此，笔者针对储层含气性定量评价问题开展研究，提出了一种有效定量表征储层天然气含气性的参数，并给出了确定该参数的评价方法，该方法在实际区块评价中的应用效果理想，以期为天然气的测井综合解释提供一条新的思路。

1 相对气体摩尔量参数的提出

含气饱和度（天然气体积占比）在天然气储层产能评价中的局限性主要表现在：天然气受其本身具有可压缩性的影响，含气体积的大小不能反映产气量的多少。在天然气充注饱含水岩石孔隙的过程中，当排烃压力高于较大孔隙的毛细管压力时，天然气驱走孔隙内的地层水而本身充注在岩石孔隙中，随着可动水的逐渐减少，天然气的含量不断增高，当天然气将可动水全部驱替后，岩石孔隙只剩下束缚流体孔隙，此时天然气便不能进入这类剩余的孔隙。由于天然气与液态流体不同，当气源的排烃压力充足时，天然气会继续向岩石孔隙内充注，此时孔隙内气体的体积不再改变，孔隙压力不断升高，天然气密度不断增大，直到排烃压力与孔隙压力平衡时为止，此时含气量增加但含气体积并未发生改变。因此，天然气的体积与绝对含气量不具有一一对应关系[15-16]，即储层的含气饱和度并不能直接反映储层的产能。

基于此，在天然气的解释评价过程中，需要提出新的解释参数来克服上述问题。天然气的物质的量不随其物理性质的改变而改变，天然气的物质的量可表示为：

式中ng表示天然气物质的量，mol；mg表示天然气质量，kg；Mg表示天然气视相对分子质量，kg/mol；ρg表示天然气的密度，kg/m3；Vg表示天然气体积，m3。

式中表示储层的孔隙度；Sw表示储层的含水饱和度。

2 相对气体摩尔量的计算方法

气体的状态方程表征气体的压力、温度与体积的相互关系，理想气体状态方程（克拉柏龙方程）表达式如下[16]：

式中p表示气体的压力，MPa；V表示气体的体积，m3；n表示气体的摩尔量，mol；T表示气体的绝对温度，K；R表示通用气体常数，8.314 MPa·m3/（mol·K）。

式（3）只适用于理想气体的表达，实际地下储层的天然气并非理想气体，目前在油气藏工程中广泛采用压缩因子状态方程：

式中Z表示气体的压缩因子。

由压缩因子状态方程可以推导储层的天然气密度，即

式中pp表示孔隙压力，MPa。

将式（5）代入式（2），相对气体摩尔量表示为：

由式（6）此可以看出，相对气体摩尔量的计算取决于储层的孔隙压力与天然气的压缩因子。

2.1 孔隙压力的计算

孔隙压力是储层孔隙空间中赋存的流体产生的压力，也叫孔隙流体压力或地层压力。常压情况下，孔隙压力为静水柱压力。地层孔隙压力确定方法很多，常用方法主要包括等效深度法、Eaton法、DC指数法、经验法等[17-20]。Eaton法是在实验的基础上利用测井资料建立的地层孔隙压力与测井响应相互关系的一种计算方法，综合考虑了压实作用与储层异常高压的形成机制，适用性强。其压力计算公式为：

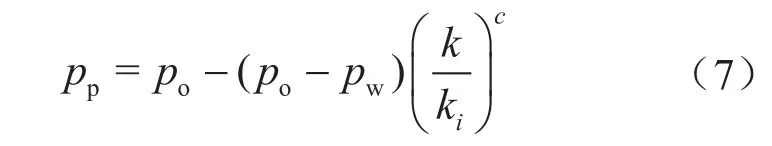
式中po表示上覆地层压力，MPa，可由密度测井积分获得；pw表示地层静水压力，MPa；k表示测井曲线参数值或测井计算值，ki为第i个计算点的计算值k对应的正常趋势线参数值（即相同深度点的正常压实趋势值）；c为Eaton指数，与区块特征及地质年代有关，当（k/ki）＞1时，改为ki/k。根据研究区块实际，本文使用声波时差曲线的对数函数（lnΔt）作为k的计算值，Δt表示声波时差，μs/m。

在实际表征孔隙压力时，由于压实作用，压力存在数值上的偏差，该偏差可以通过校正系数进行校正。因此，孔隙压力方程可改写为：

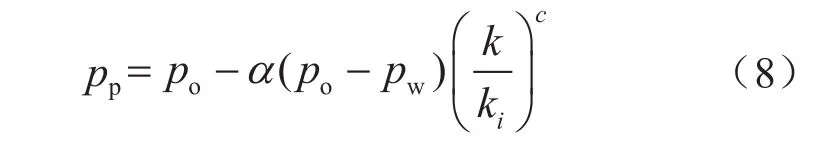
式中校正系数α和c由拟合确定。

2.2 天然气压缩因子的确定

由于储层中的天然气是由低碳数的轻烃混合组成，其压缩因子受天然气的组分、温度、压力等因素影响。天然气的压缩因子可采用实验测试、经验公式及S—K图版法进行求取[12]，采用S—K图版法确定的压缩因子精度高且相对简便。

S—K图版是Standing与Katz根据实验测试资料及状态方程推导建立的压缩因子—视对比压力和视对比温度关系图版[13]，也称为天然气的双参数压缩因子图版，如图1所示。

图1 天然气的双参数压缩因子图版

结合式（8）与图1，代入式（6），即可得到储层的相对气体摩尔量参数。

3 应用实例

按照上述计算过程，选取鄂尔多斯盆地苏里格致密气田某区X井资料进行综合处理计算，上覆地层压力由密度积分可得随深度（H）的变化公式为：

利用声波时差资料确定苏里格致密气田某区储层正常压实趋势线，建立lnΔt与深度的函数关系，可得压实关系曲线（图2）。

图2 苏里格致密气田某区声波时差测井曲线正常压实趋势图

通过式（14）即可根据声波时差曲线确定不同深度的正常压实趋势值，并且根据每个深度点的实测值，确定方程（7）中k/ki的值。该区块实际压力方程式为：

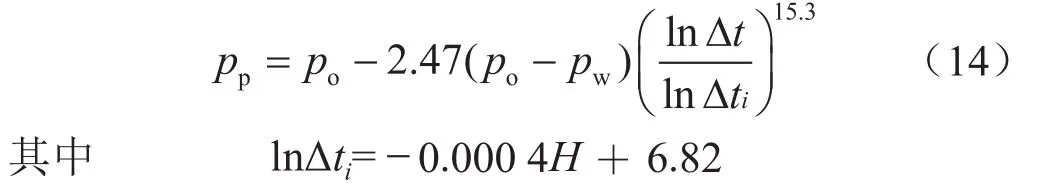
式中lnΔti表示第i个深度点的声波时差对数lnΔt对应的正常趋势线参数值。

含水饱和度（Sw）计算采用Archie公式，即

式中a表示与岩石有关的比例系数，b表示与岩性有关的常数，m表示岩石胶结指数，n表示饱和度指数，均为常数，无量纲；Rw表示地层水电阻率，Ω·m；Rt表示地层电阻率，Ω·m。

根据公式（6），可计算纵向连续的相对气体摩尔量参数，对X井进行计算，处理结果如图3所示。试气结果显示，该测试井段有4个含气层，由上至下分别为：微含气层、含气层、气层、气层，其物性参数差异不大。将各含气储层的相对气体摩尔量计算结果与含气饱和度计算结果对比，可以看到各含气级别储层的相对气体摩尔量数值差异显著，且与中子—密度差值程度有着相同的指示特征，说明相对气体摩尔量参数可以较好地指示储层的含气性，而含气饱和度参数在本解释井段中不能较好区分气层与含气层。

从表1中可以看出，含气饱和度最高的Ⅱ层试气结果为含气层，相对气体摩尔量仅为130 mol/m3，含气饱和度相对低的Ⅲ层，相对气体摩尔量数值明显高于Ⅱ层，与试气结果高度一致，说明相对气体摩尔量参数较含气饱和度相比具有更强的天然气产能识别能力。综上分析表明，储层的含气饱和度与储层的含气性不是一一对应关系，即高含气饱和度岩石在某些情况下并不发育较好的气层，相对中等含气饱和度的岩石也可以发育高产气层。