微尺度通道内稀薄气体高阶努森数渗透率修正模型
2019-05-13卢银彬
卢 银 彬
西安石油大学机械工程学院
0 引言
页岩气储集在低孔隙度、特低渗透率暗色泥页岩或高碳泥页岩层系中[1-2],这些层系孔隙的尺寸主要属于微纳米级。已有的研究表明,当气体流经常规通道时,由于流动通道的特征尺寸远大于气体分子运动的平均自由程,可视气体为连续介质,采用经典Hagen-Poiseuille理论公式计算气体流量[3]。但是,当气体在微纳米级孔隙通道中流动时,由于通道尺寸接近甚至小于气体分子运动的平均自由程,此时气体流动会产生稀薄效应,宏观上表现为相同压降梯度下获得的气体流量大于Hagen-Poiseuille理论公式计算的流量,连续性假设不再适用,传统Navier-Stokes方程失效。刘杰等[4]认为在页岩纳米级孔隙中气体流态为滑脱流或过渡流,不存在连续流,且孔隙越小,压力越低,滑脱流越弱,气体稀薄效应越强。定量研究页岩气流动的稀薄效应,对页岩气井产能的精确评价有重要意义[5]。目前已有较多一阶和二阶滑移模型用于描述气体稀薄效应,这些模型通过采用格子Boltzmann方法(LBM)、直接模拟蒙特卡洛法(Direct Simulation Monte Carlo,简称DSMC法)或者实验等方法求得模型中的滑移系数,但所建立的模型均缺乏普适性。为此,笔者首先采用R26矩方法对平板微通道中气体的流动进行数值模拟,并与DSMC法、R13矩方法的模拟结果进行对比,然后基于R26矩方法的模拟结果建立平板微通道与圆管微通道的高阶努森数气体渗透率修正模型,计算不同努森数对应的气体渗透率修正系数,并与Tang模型预测结果、实验数据及线性Boltzmann方程解进行对比。所建立的模型预测精度高且具有普适性。
1 含一阶和二阶滑移系数的气体渗透率修正模型
1879年,Maxwell[6]通过理论分析研究,首次提出气体流动时在壁面存在滑移效应。而后,Knudsen[7]于1909年提出采用努森数(Kn)来描述气体稀薄效应,Kn的计算式为:

式中λ表示分子平均自由程,m;R表示流动通道特征尺寸,m,对于平板通道为平板间距,对于圆管通道为圆管直径,m;μ表示气体动力黏度,Pa·s;p表示气体平均压力,Pa;Rg表示气体常数,J/(mol·K);T表示温度,K;M表示气体摩尔质量,g/mol。
Kn越大,气体稀薄效应越显著。根据Kn的取值范围划分气体流动区间:当Kn<10-3时,为无滑移区,即连续区;当10-3≤Kn≤10-1时,为滑移区;当10-1<Kn≤10时,为过渡区;当Kn>10时,为自由分子区。
1999年,Beskok和Karniadakis[8]推导出稀薄气体在毛细管中的流量计算式,即

式中Q表示气体体积流量,m3/s; 表示稀薄气体系数,无量纲,在滑移区取值为-1;r表示圆管半径,m;Δp表示流体在毛细管进出口处的压降,Pa;Lt表示毛细管总长度,m。
当气体在微纳米尺度通道中流动时存在稀薄效应,采用含努森数的函数对气体在通道内的流量(或渗透率)进行修正,即在相同压力梯度下气体实际流量与采用Hagen-Poiseuille理论公式计算流量的比值(或气体表观渗透率与岩石绝对渗透率的比值)可用含努森数的函数f(Kn)表示,即
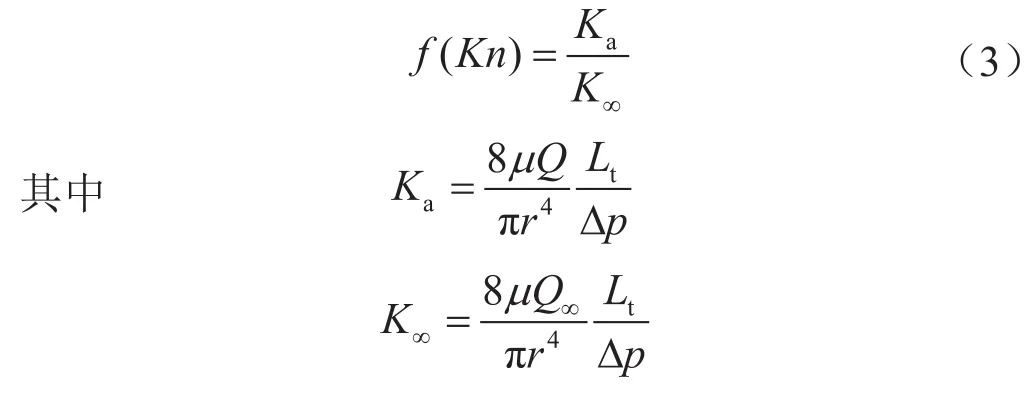
式中Ka表示表观渗透率,m2;K∞表示岩石绝对渗透率,m2;Q∞表示无稀薄效应时气体体积流量,m3/s。
对于无稀薄效应的气体或者液体,其渗透率与流体物性无关,仅与通道结构相关,与岩石绝对渗透率相等。
根据公式(3)并结合式(2)得到与流体物性相关的气体渗透率修正系数的计算式,即

2005年,Tang等[9]将二阶滑移边界条件应用于Navier-Stokes方程中,获得稀薄气体在平板通道中的渗透率修正模型,即
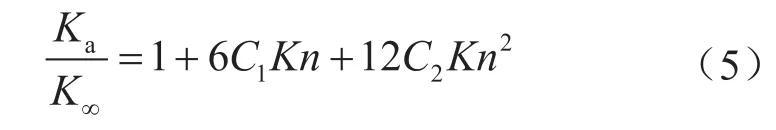
式中C1和C2分别表示一阶、二阶滑移系数。
同时,Tang等[9]将该修正模型推导至圆管通道,获得圆管中气体渗透率修正模型,即
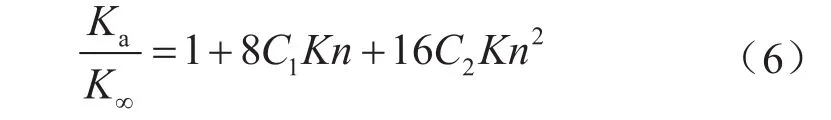
表1中列出了几组常见的滑移系数C1和C2。
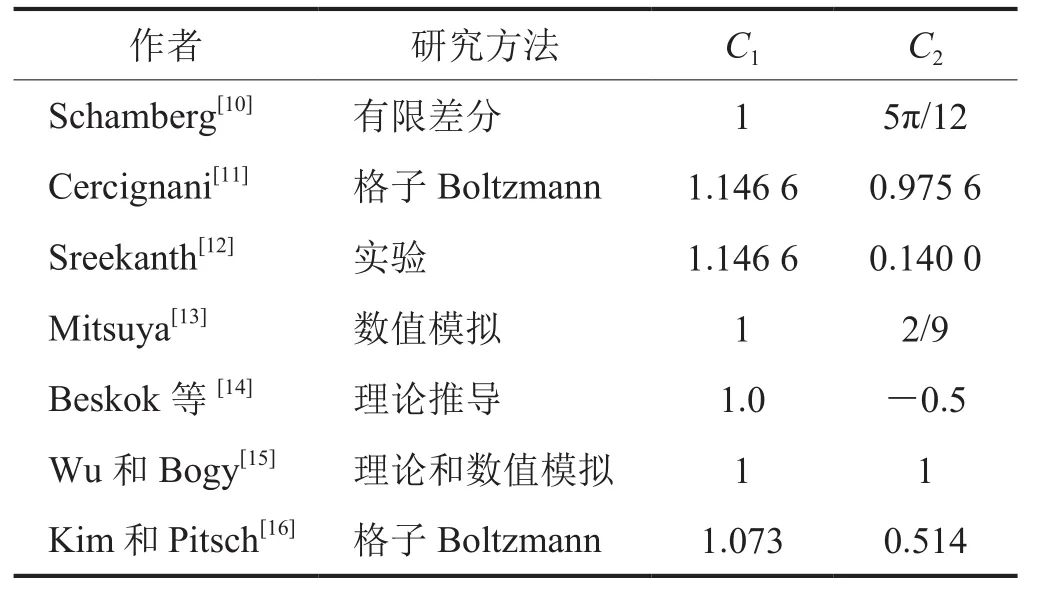
表1 滑移系数C1、C2统计表
2 矩方法
矩方程方法(简称矩方法)是一种介于传统流体力学计算方法和粒子算法之间的方法。1949年,Grad[17]首次推导出包含13个矩变量的Grad十三阶矩方法(简称G13矩方法),其后Struchtrup[18]发展了正则化十三阶矩方法(简称R13矩方法),R26矩方法[19]是基于R13矩方法获得的。2009年,Gu和Emerson[20]采用R26矩方法对非平衡气体流动传热问题进行数值模拟,指出该方法能够准确捕捉到气体在滑移和早期过渡区的稀薄行为,且计算量远小于粒子方法(如DSMC法),是一种值得采用的研究方法。
2.1 矩方程
当气体在通道中流动而速度、温度等参数不随时间发生改变时,可视气体流动已达到平衡状态。当气体流动处于平衡状态或者接近于平衡状态时,对气体在流动相空间分子分布函数(g)的5个矩变量(密度、温度以及三维空间x、y、z方向上的速度)建立质量、动量和能量守恒方程。当气体流动偏离平衡状态时,稀薄效应凸显,需要在矩方程中引入更高阶的矩变量来描述气体流动。矩方法中,Grad[19]通过引入麦克斯韦分布函数(gM)[21],采用Hermite多项式将分子分布函数展开,即
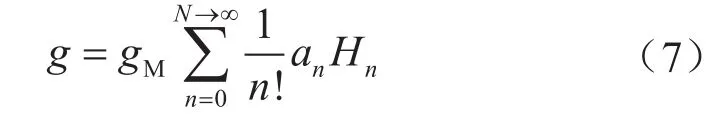
式中g表示分子分布函数;gM表示麦克斯韦分布函数;N表示展开后的总项数;an表示第n项矩的线性组合系数;Hn表示第n项Hermite多项式。
当N趋于∞,采用Hermite多项式可准确重构分子分布函数。而实际计算时,无法求解无穷项,必须根据实际问题,确定需要展开的项数后截断g函数。在Grad的理论中,截断后的g函数记作gG,其中包含的矩被称为“Grad矩集合”,即Grad Moment Manifold(简称GMM)[19],这些矩的控制方程可通过Boltzmann方程推导获得,简称为矩方程。采用四阶截断分布函数可以获得26个矩变量构成的方程组,通过增加矩变量数量可以提高气体在滑移和早期过渡区流动行为的描述精度。
2.2 数值求解方法
为了在传统流体力学方程基础上求解矩方程,需要根据矩方程中非梯度输运项与梯度输运项的特点修改原始矩变量,从而使矩方程能描述对流扩散过程,经改写后的方程组可用于模拟气体低速流动下的非平衡行为。
采用有限体积法数值求解改写后的矩方程,应用中心差分格式离散扩散项和源项、CUBISTA格式离散矩方程中的对流项[22],同时利用交错网格上的SIMPLE算法耦合速度与压力[23-24],使用多块网格技术生成复杂区域中的计算网格。如需了解更多细节,可参阅本文参考文献[20,25],此不赘述。
2.3 边界条件
模拟计算气体流动时需要限定气体流动区域,为构造R26矩方程的边界条件,利用分子分布函数在五阶截断的近似表达式[19],结合麦克斯韦动理论边界条件[26],获得描述矩变量[20,25]的动理论模型。
3 平板微通道中气体稀薄效应
通过R26矩方法模拟气体在平板微通道中的流动行为。两平行平板长度(L)均为100 μm,板间间距(h)为1 μm。模拟气体为氮气,温度(T)为300 K。同时,将h作为特征尺寸,采用Kn描述气体的非平衡状态。对于平板微通道,K∞为h2的1/12[26],Ka可由Darcy定律计算获得。
3.1 R26矩方法准确性验证
DSMC法从微观角度出发,考虑分子之间的作用力以及分子与壁面之间的碰撞作用,通过模拟大量分子的运动行为,统计获得气体的宏观物性以及运动等参数[27-28]。通常认为DSMC法的模拟结果非常准确,本文参考文献[29]采用DSMC法,模拟Kn为0.038 6、0.178 5和0.537 1下气体在平板微通道中的流动。为验证R26矩方法的准确性,将模拟结果与本文参考文献[29-30]的计算数据进行对比(图1),图1中纵坐标为,其中u表示流体流速,umax表示两平板中心处的气体最大流速;横坐标为 ,Y表示距离平板中心线的距离。可以看出,R26矩方法的模拟结果与DSMC计算数据能够很好地吻合,而R13矩方法的模拟结果[30]在Kn较大(取值为0.537 1)时,与DSMC法的模拟结果存在较大偏差,准确性较R26矩方法偏低,这是因为R26矩方法能够较准确地捕捉到紧靠固体壁面克努森层的气体滑移特性[31]。可见,采用R26矩方法模拟研究气体稀薄效应具有较高的计算精度。
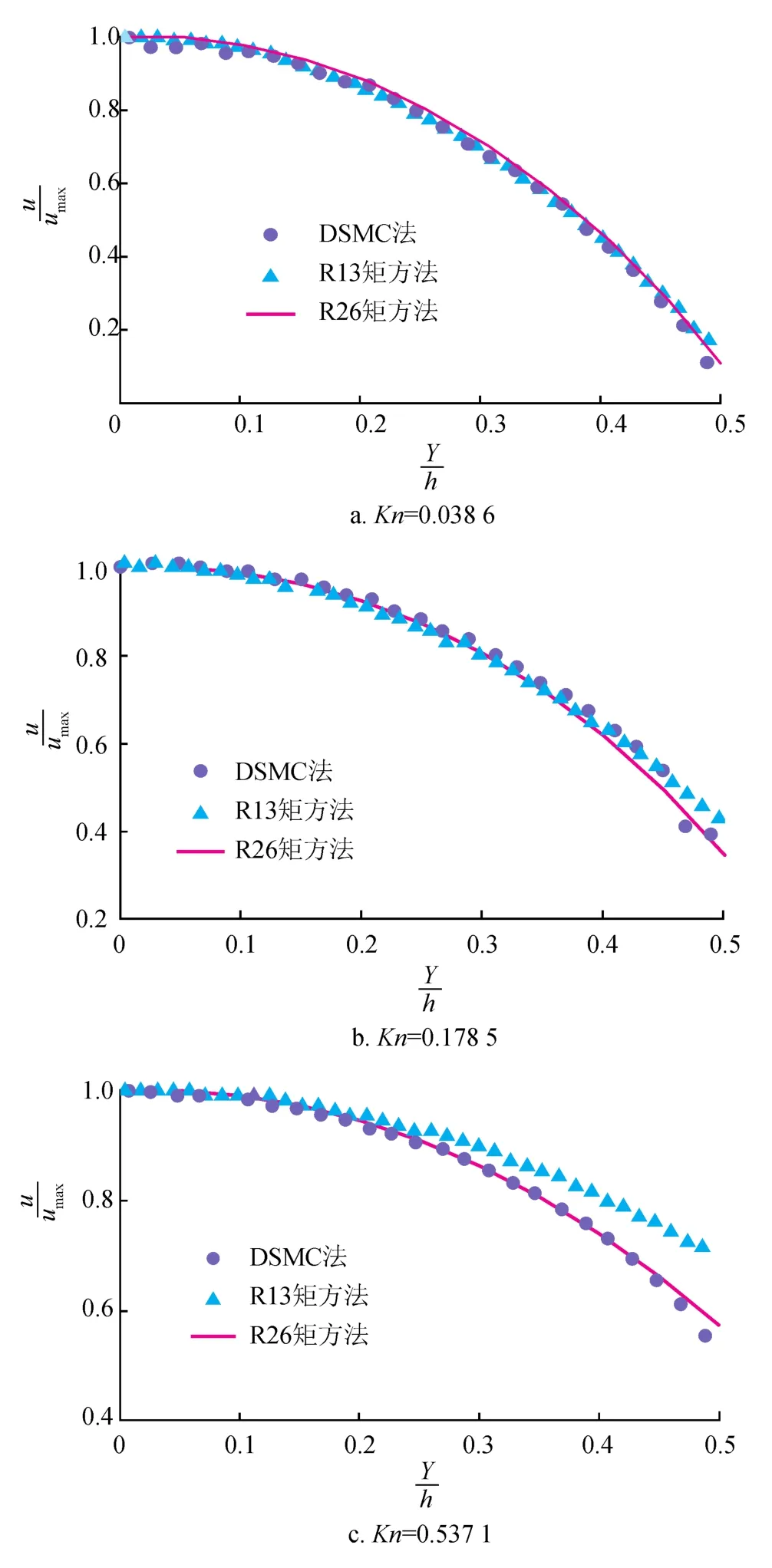
图1 R26矩方法、R13矩方法与DSMC法模拟结果对比图
3.2 高阶努森数气体渗透率修正模型
目前大部分气体表观渗透率修正模型多为一阶和二阶修正,且需要选择合适的滑移系数代入模型,由于提出的系数众多,增加了选择难度。2007年,Zhu等[32]首次提出高阶努森数气体渗透率修正模型,但未给出式中常数A的具体数值及参数α的函数式,模型计算式为:
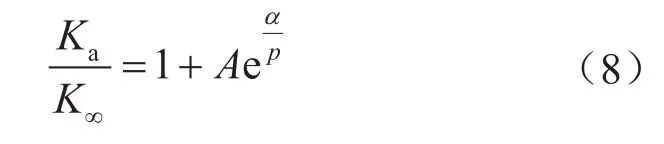
结合分析Tang等[9]提出气体渗透率修正模型,如式(5)、(6)所示,笔者认为该模型中的参数A应取值为6(针对平板)和8(针对圆管),但仍需对指数进行确定。
笔者提出平板微通道中高阶努森数气体渗透率修正模型表达式为:

式中a、b、c分别表示修正系数。
为求取式(9)中的3个参数a、b和c,采用R26矩方法模拟Kn介于0.01~1.00时气体在平板微通道中的流动,计算得到气体表观渗透率,结合式(3)求得气体渗透率修正系数,将数据点拟合,得到式(9)中a为3.94、b为0.333和c为-3.94(图2)。
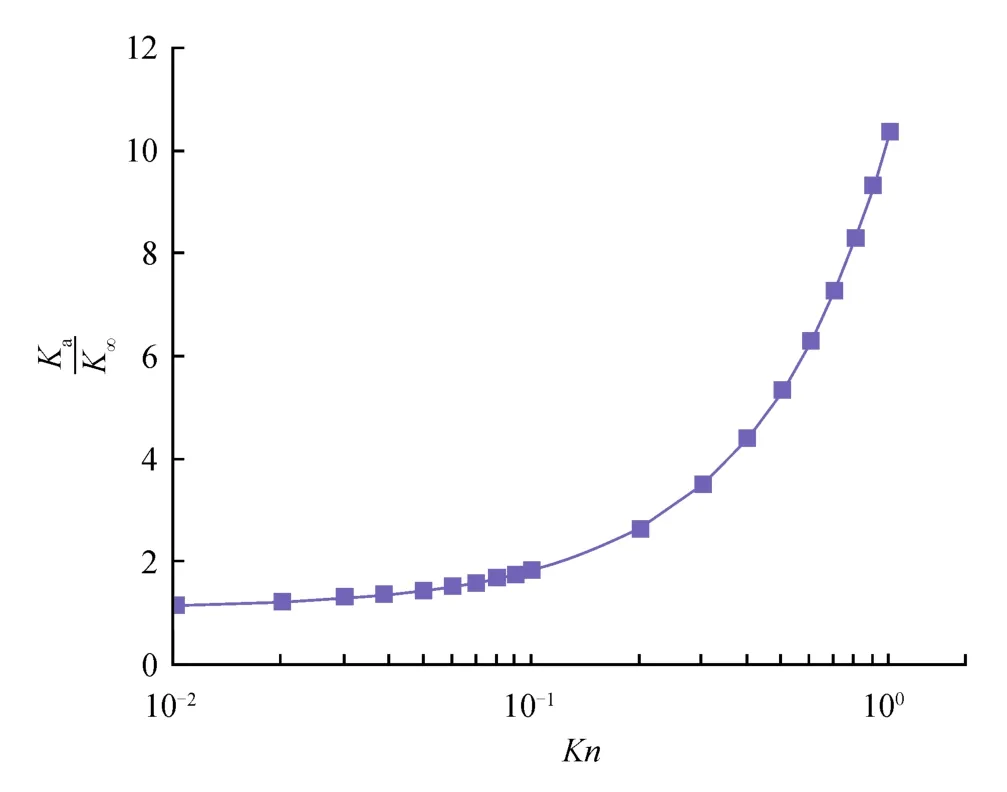
图2 平板微通道中Kn与关系曲线图
泰勒展开式(9),得
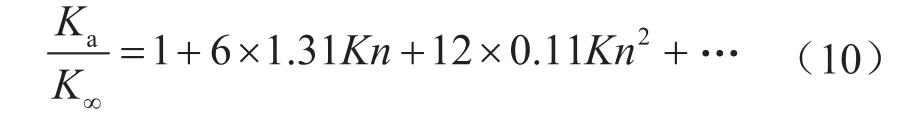
可见,当泰勒展开后的高阶努森数气体渗透率修正模型截断至Kn时,即为一阶努森数气体渗透率修正模型,当截断至Kn2时,即为二阶努森数气体渗透率修正模型。泰勒展开后项数越多,模型预测结果越准确。由此可见,本文提出高阶努森数气体渗透率修正模型具有两大优点:①预测精度高;②具有普适性,可以直接使用。
3.3 模型验证
采用本文参考文献[33-34]中的实验数据以及线性Boltzmann方程解[35]验证模型的有效性,如图3所示,线性Boltzmann方程解具有较高的计算精度,本文模型能够较好地预测实验结果,并且与线性Boltzmann方程解非常吻合。将表1中的滑移系数[10-16]代入Tang模型[9],如式(5)所示,可以看出,Tang模型[9]采用不同滑移系数进行预测,多组预测结果与实验结果存在较大偏差,虽然采用Kim和Pitsch[16]提出的参数预测的结果与实验结果较吻合,但仍与线性Boltzmann方程解[35]存在一定差距。
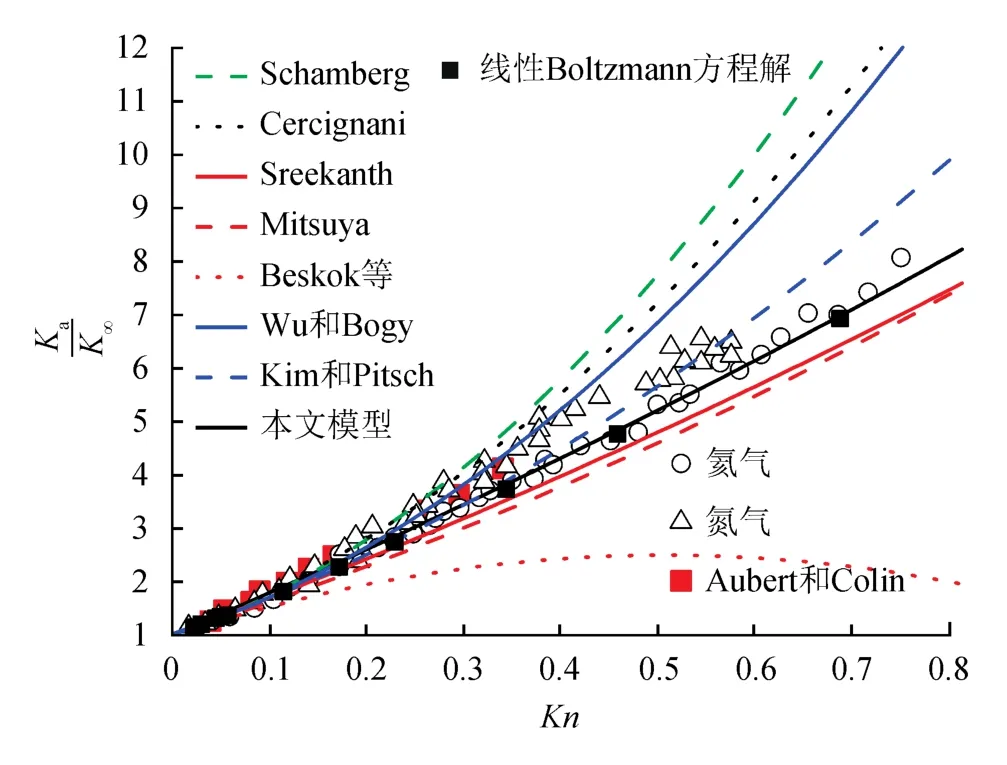
图3 基于本文模型、考虑不同滑移系数的Tang模型、实验数据和线性Boltzmann方程解的Kn与对比图(平板微通道)
为进一步验证模型的准确性以及确认Kim和Pitsch[16]提出系数的准确性,再次将本文模型预测结果与本文参考文献[36]的实验数据进行对比,可以看出,本文模型预测结果与实验结果总体较吻合,但是Kim和Pitsch提出的系数应用于Tang模型[9]在努森数较大时存在较大偏差(图4)。而且,有学者指出应针对不同气体选择不同的系数C1与C2[37],这更增加了选择难度。若对滑移系数感兴趣,可参阅本文参考文献[38]。

图4 本文模型、Tang模型和实验数据结果对比图(平板微通道)
4 圆管微通道中气体稀薄效应
下面模拟N2在直径为1 μm的毛细管中的流动情况,气体努森数介于0.01~1.00。
根据模拟结果拟合获得高阶努森数气体渗透率修正模型(图5),具体表达式为:
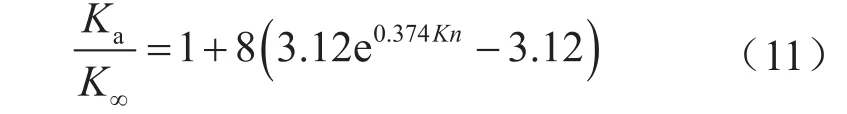
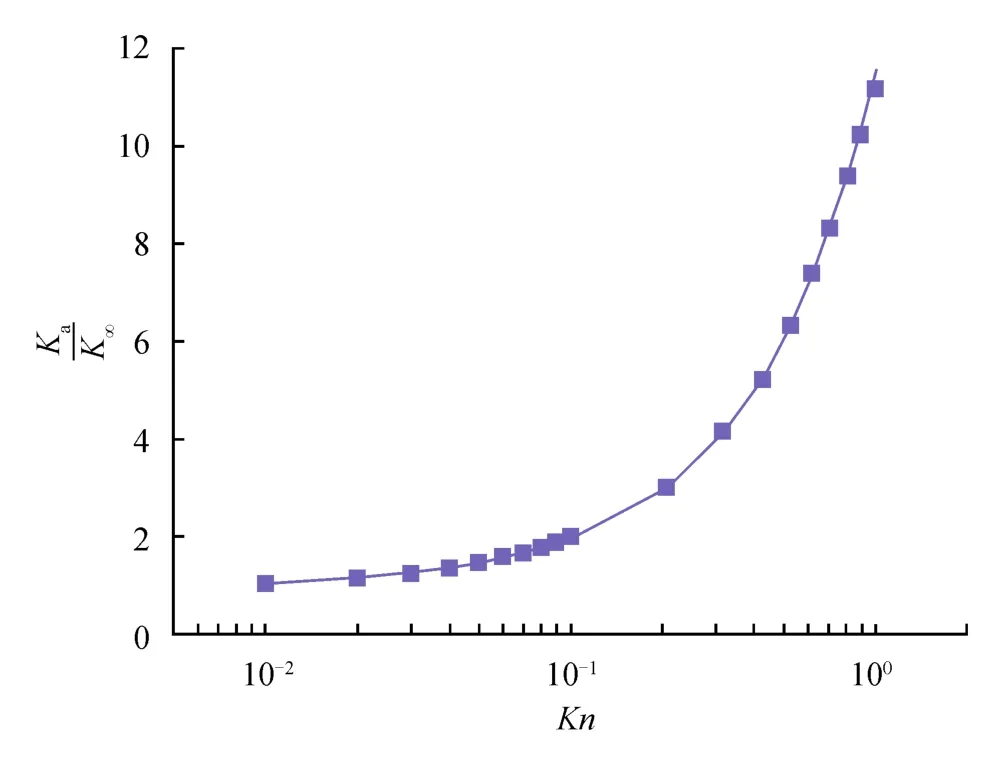
图5 圆管微通道中Kn与关系曲线图
泰勒展开式(11),有
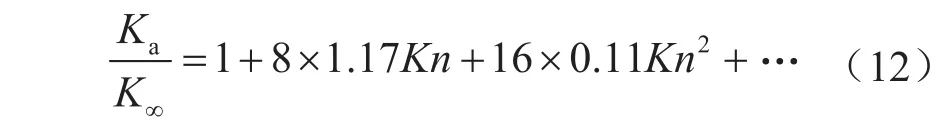
将本文模型预测结果和线性Boltzmann方程解[39]进行对比(图6),可以看出,圆管中本文模型与线性Boltzmann方程解能够很好地吻合,证实了本文模型的准确性。另外,不同滑移系数[10-16]应用到Tang模型后预测结果差异大,且大多数预测结果与线性Boltzmann方程解存在较大偏差。
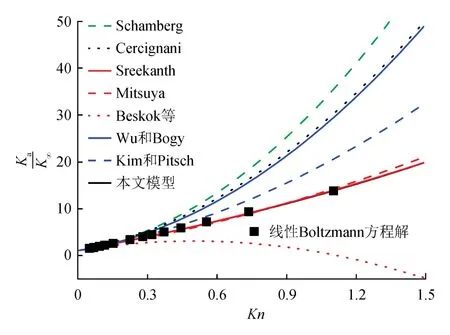
图6 本文模型、Tang模型和线性Boltzmann方程解结果对比图(圆管微通道)
5 结论
1)采用R26矩方法描述气体稀薄效应,其模拟结果与DSMC计算数据吻合情况良好,且计算精度高于R13矩方法。
2)针对平板微通道和圆管微通道分别建立高阶努森数气体渗透率修正模型,前者预测结果与实验结果、线性Boltzmann方程解吻合情况好,后者预测结果也与线性Boltzmann方程解吻合情况好,所建立的模型预测精度高且具有普适性。
