基于幂函数形式物质平衡方法的高压、超高压气藏储量评价
2019-05-13孙贺东王宏宇朱松柏聂海峰李原杰李松林常宝华
孙贺东 王宏宇 朱松柏 聂海峰 刘 杨 李原杰李松林 曹 雯 常宝华
1.中国石油勘探开发研究院 2.中国石油塔里木油田公司
0 引言
高压(压力系数介于1.3~1.8)、超高压(压力系数大于1.8)气藏几乎遍布于世界各地,埋深从只有几百米到8 000 m不等[1]。2000年以来,中国高压、超高压气藏勘探开发业务发展迅速,探明储量与产气量快速增长。截至2016年底,我国已累计探明超深层(埋藏深度大于4 500 m)气藏天然气地质储量2.6×1012m3,年产气量突破300×108m3,已成为天然气增储上产和效益增长的主体[2]。大量的实际资料表明高压、超高压气藏的油藏工程意义特殊,沿用过去的方法计算储量,误差竟达100%[3]。常压封闭气藏压降曲线为直线[4];当有地层水侵入气藏时,压降曲线上翘;不带水域的高压、超高压气藏压降曲线为两条斜率不同的直线段,且第1直线段的斜率明显低于第2直线段的斜率[3,5]。但是,第2直线段一般出现较晚,可能需要采出气藏真实地质储量的20%~25%[6],拐点出现的早晚既与岩石压缩特性及其应力敏感性有关,也与天然气物性有关,拐点出现的时刻尚无理论计算公式。对于实际高压、超高压气藏,岩石和束缚水的变形是随储层压力下降而连续变化的,所以压降曲线为拟抛物线[7],且岩石压缩系数和束缚水饱和度对压降曲线的形态有重要影响,两直线段的处理方式仅仅是对曲线的近似处理。
高压、超高压气藏物质平衡法可划分为两类,第1类需要岩石和流体压缩系数等参数,主要有Hammerlindl修正压缩系数法[3]、Ramagost-Farshad修正线性回归法[8]、Bourgoyne二元回归法[9]、Fetkovich曲线拟合法[10]等,由于岩石和流体压缩系数很难准确确定,且物质平衡曲线Gp关系曲线)应采用累积有效压缩系数表示,因此,该类方法的应用受到较大限制;第2类则无需岩石和流体压缩系数等参数,仅需生产历史数据就能确定累积有效压缩系数和储量等,主要有Roach直线回归法[11](对原始压力参数敏感)、Ambastha典型曲线拟合法[12]、Gan二段式多图版曲线拟合法[13],Gonzalez抛物式多图版曲线拟合法[14]及其衍生法[15-19]等。Gonzalez及其衍生方法均假设储量和累积有效压缩系数呈线性关系。
为了提高此类气藏储量计算结果的可靠性,本文将在Gonzalez方法[14]的基础上,建立储量和累积有效压缩系数呈幂函数形式的高压、超高压气藏物质平衡方程,并结合20个国外已开发高压、超高压气藏实例,确定幂指数经验值,统计分析视储层压力衰竭程度和采出程度对储量计算结果的影响,确定影响储量评价可靠性的关键参数(视储层压力衰竭程度)的临界值,并与两段式临界值进行对比。
1 天然气储量和累积有效压缩系数近似关系
1.1 高压、超高压气藏物质平衡方程
若不考虑水侵量及注气量,高压、超高压气藏物质平衡方程[10]可以表示为:
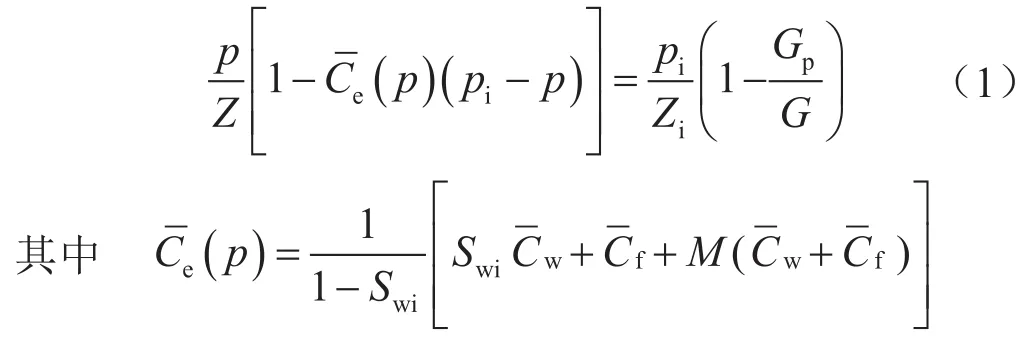
式中p表示储层平均压力,MPa;Z表示天然气偏差因子,无量纲表示累积有效压缩系数,MPa-1;pi表示原始状态下储层平均压力,MPa;Zi表示原始状态下天然气偏差因子,无量纲;Gp表示天然气采出量,108m3; G表示天然气储量,108m3;Swi表示束缚水饱和度;表示累积束缚水有效压缩系数,MPa-1;表示累积储层有效压缩系数,是压力和原始压力的函数,MPa-1;M表示水体倍数。
1.2 Gonzalez线性近似关系式
Gonzalez等[14]基于一组干气气藏模拟数据提出线性近似关系式,即
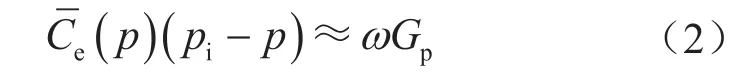
式中ω表示影响因子,(108m3)-1。将式(2)代入式(1),引入无量纲视储层压力(pD),变换为:
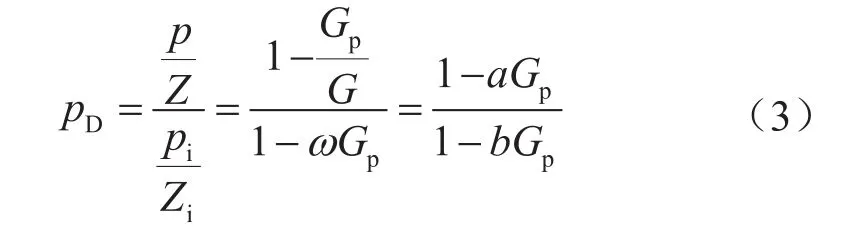
式(3)中的系数a和b可通过非线性回归的方式[20]得到。若,根据泰勒级数展开式,有
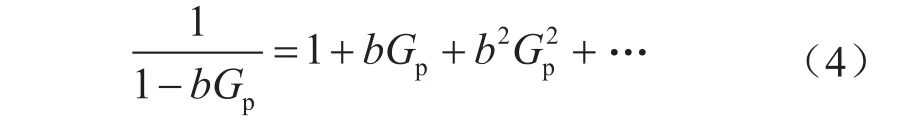
将式(4)代入式(3),即可得到抛物型[14-18]及三次型[19]关系式,分别为:
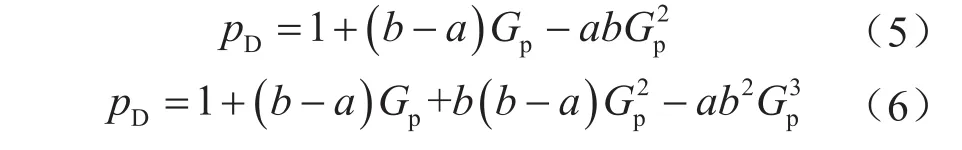
1.3 幂函数形式近似关系式
根据式(1),有
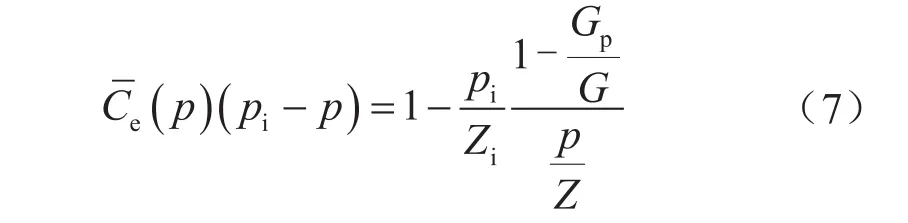
下面以美国Anderson“L”气藏[5]为例,验证与呈何种相关关系。该气藏埋深为3 404.5 m,压力系数为1.907 MPa/100 m,储层原始压力为65.55 MPa,温度为130.0 ℃,束缚水饱和度为0.35,有效厚度为22.86 m,储层水压缩系数为4.351×10-4MPa-1,岩石压缩系数为2.176×10-3MPa-1,容积法地质储量为19.68×108m3。

表1 Anderson“L”气藏生产历史及计算过程数据表
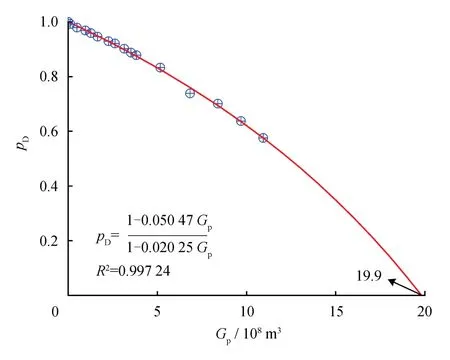
图1 Anderson“L”气藏pD—Gp非线性回归拟合图
根据该气藏生产历史数据(表1),首先绘制pD—Gp关系图,如图1所示,应用式(3)进行非线性回归,得天然气储量为19.9×108m3,根据式(7)计算;然后绘制与 双对数图,如图2所示,与并不呈线性关系[14](斜率为1.0),而有12.8%的偏差,双对数坐标下的线性趋势线斜率为1.128 34,即与呈幂函数关系。
将国外20个已开发高压、超高压气藏[22]绘制在一张双对数坐标图上,线性回归得到幂指数经验值为1.028 47,其上限值为1.115 67(图3)。国外20个已开发高压、超高压气藏的基础参数如表2所示。

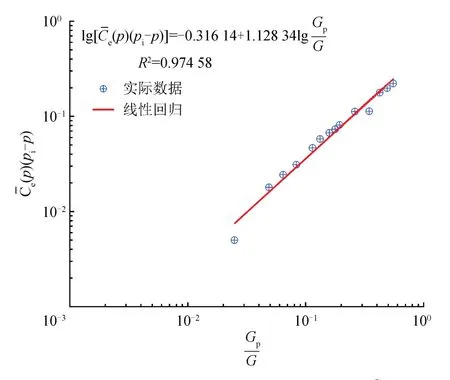
图2 Anderson“L”气藏双对数曲线线性回归拟合图
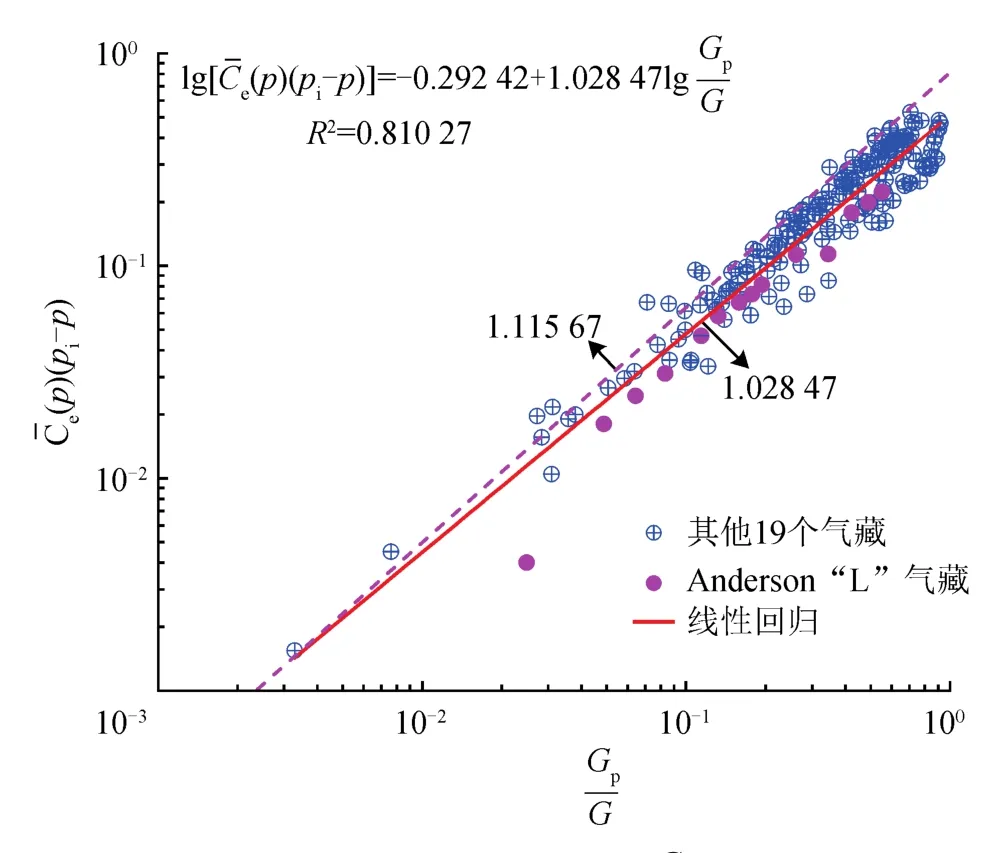
图3 国外20个气藏双对数曲线线性回归拟合图

表2 国外20个气藏基础参数与储量统计表
将式(8)代入式(1),结合pD与系数a、b的定义,有
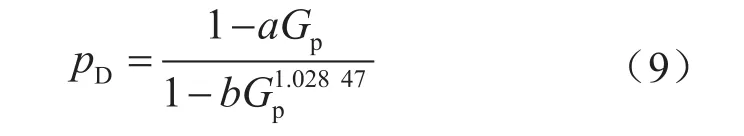
上式即为幂函数形式的高压、超高压气藏物质平衡方程。
1.4 经典文献实例
分别用式(3)、(5)、(9)计算 Anderson“L”气藏储量,结果如图4所示,式(9)的计算结果(19.50×108m3)与容积法储量(19.68×108m3)最接近;如表3所示,式(3)、(9)的计算结果较其他文献中使用的方法有明显优势。
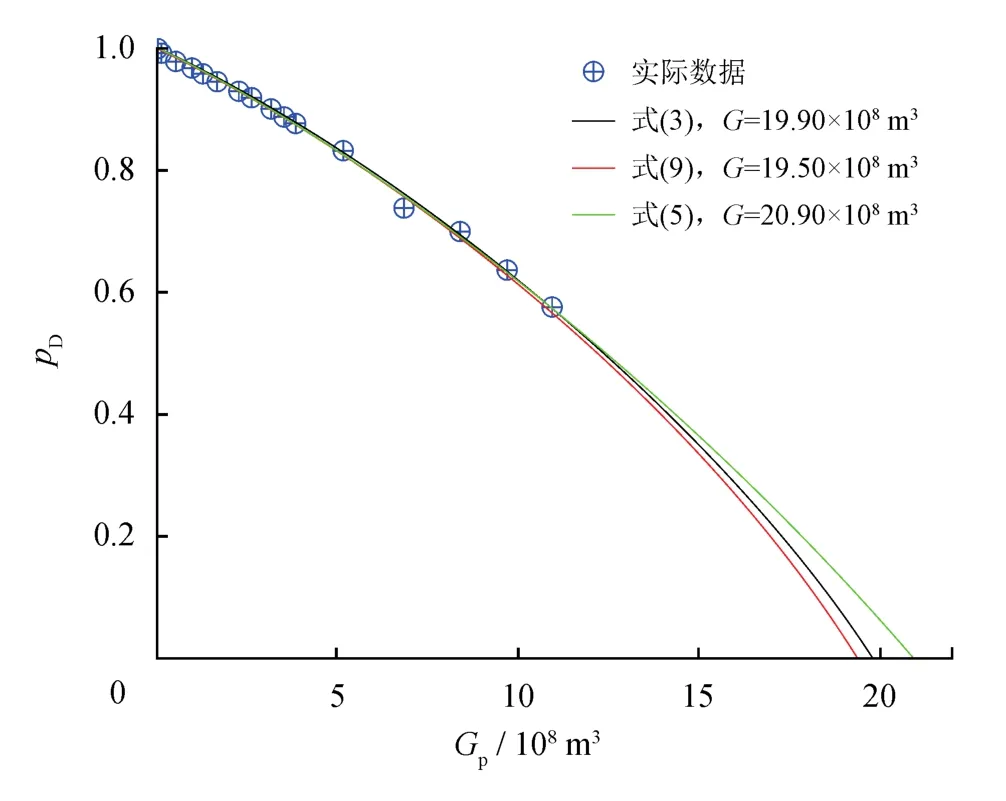
图4 Anderson“L”气藏pD—Gp非线性回归拟合结果对比图

表3 不同方法计算Anderson“L”气藏储量结果表
分别用式(9)计算前述国外20个已开发高压、超高压气藏的储量,与Gan方法、Gonzalez方法的计算结果均较接近(表4)。当视储层压力衰竭程度较小时,计算结果都具有一定的不确定性,如1-pD=0.16时,式(5)、(6)、(9)的储量计算结果差异较大(图5)。
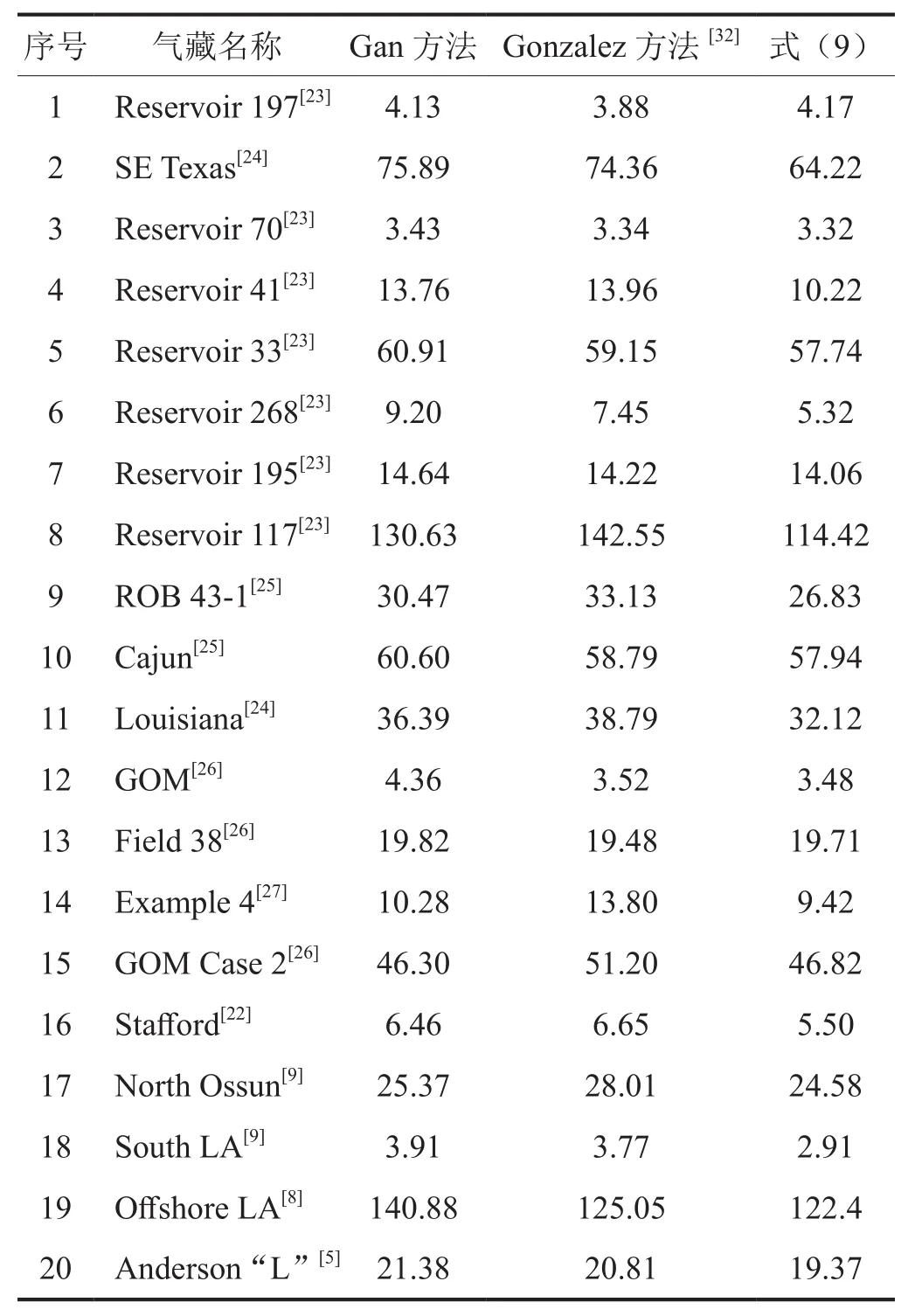
表4 国外20个已开发高压、超高压气藏储量对比表 108 m3
1.5 视储层压力衰竭程度( -pD)与采出程度
以Gan方法为代表的直线两段式方法,拐点处对应的1-pD介于0.14~0.38,平均为0.23,如图6-a所示;第2直线段可计算天然气储量时间点对应的1-pD介于0.23~0.50,平均为0.33,如图6-b所示;采用该方法计算气藏储量,采出程度介于33%~65%时,储量计算误差小于10%,采出程度平均为45%。
采用式(9),以采用前期部分点计算的天然气储量与采用生产历史所有点计算的天然气储量误差低于10%为统计标准,1-pD介于0.16~0.62,平均为0.33,如图7所示;采出程度介于28%~62%,平均为48%,如图8所示。
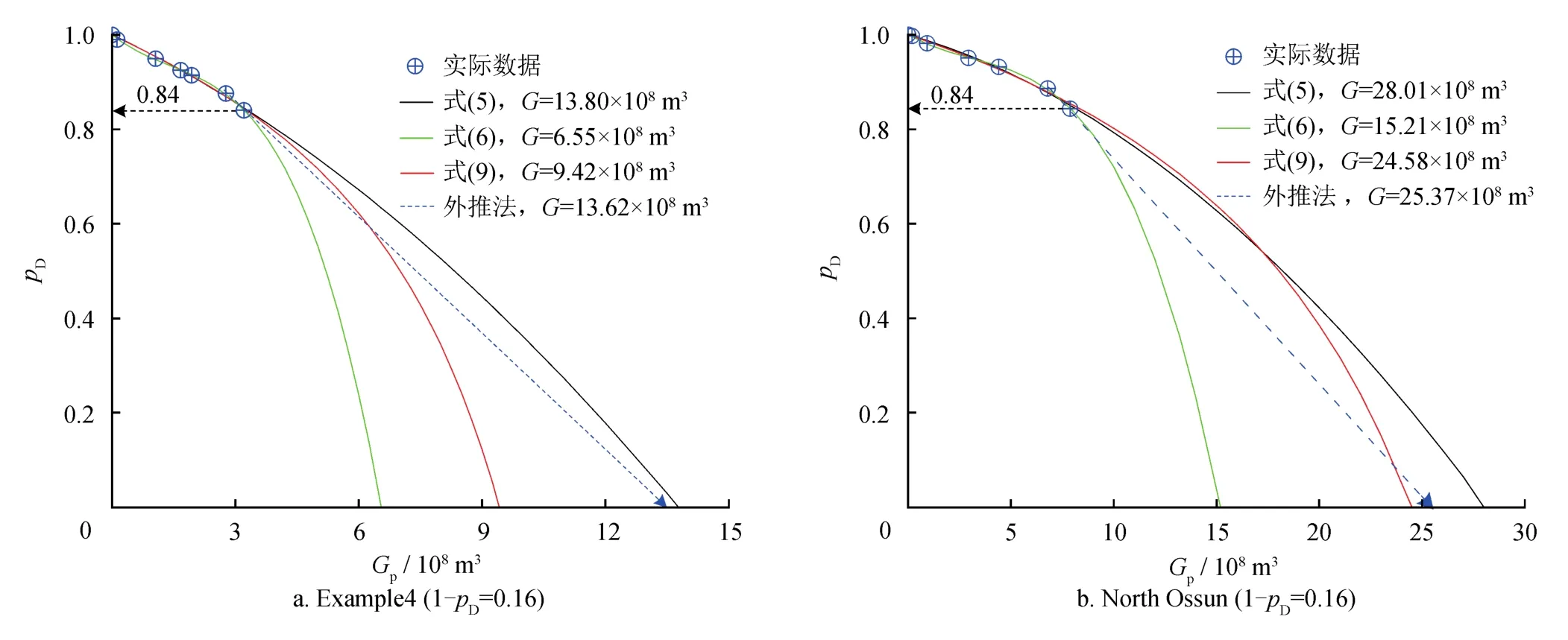
图5 视储层压力衰竭程度较小时不同计算方法计算结果对比图
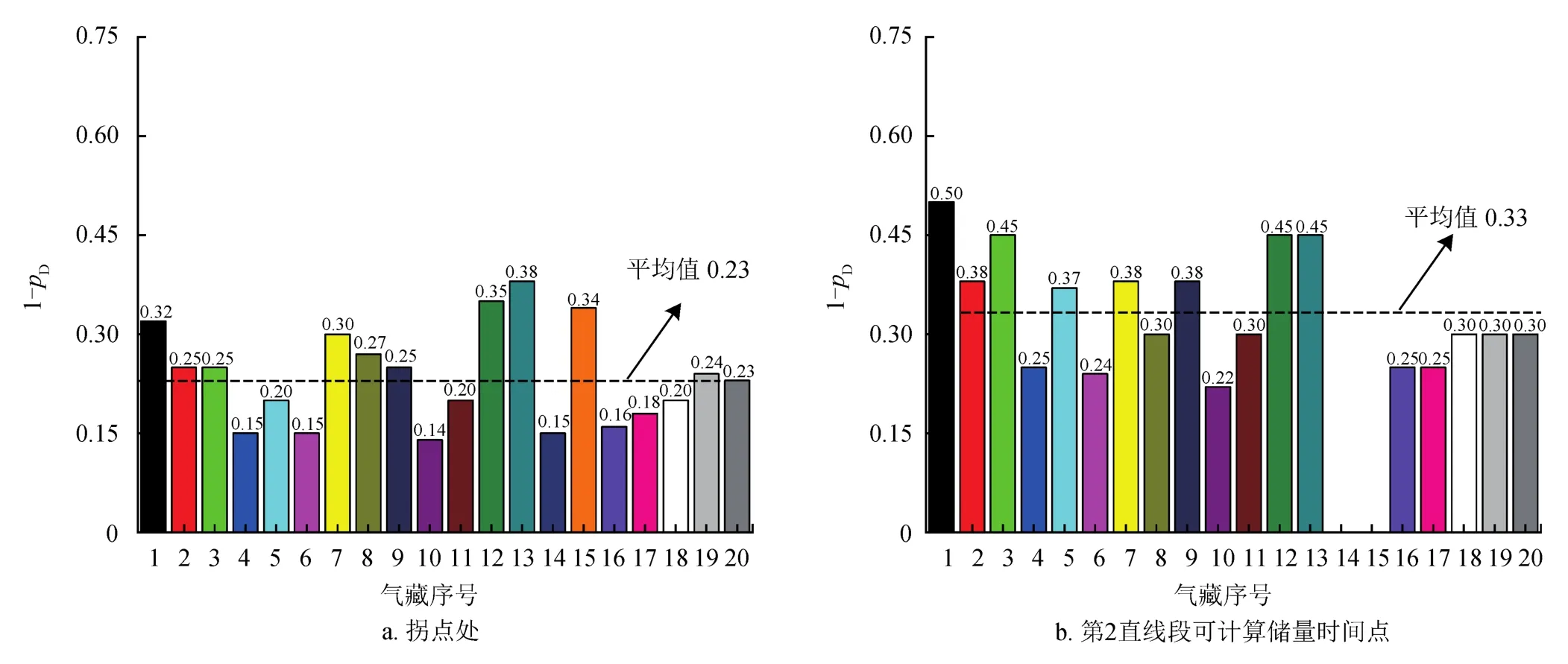
图6 Gan方法直线段拐点及第2直线段可计算天然气储量时间点对应的视储层压力衰竭程度统计图
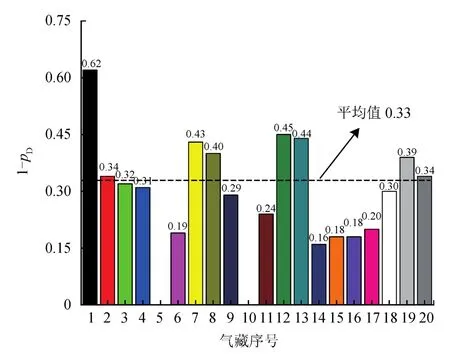
图7 储量计算误差小于10%对应视储层压力衰竭程度统计图
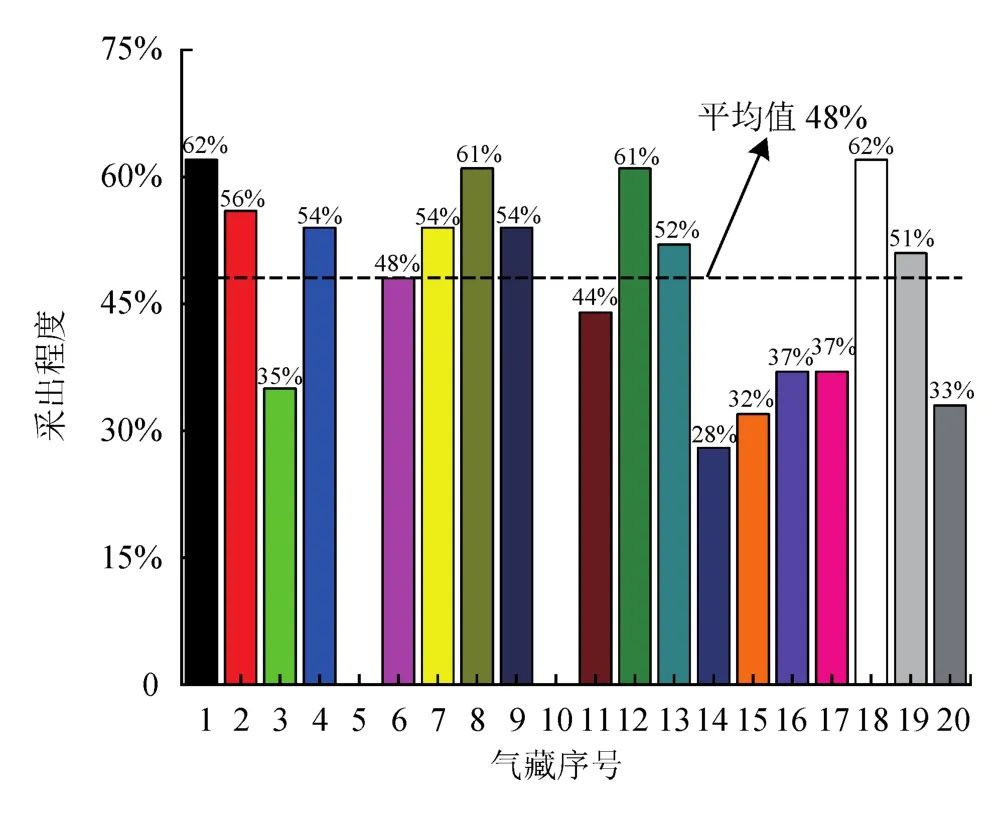
图8 储量计算误差小于10%对应采出程度统计图
2 实例分析
2.1 高压有水气藏计算实例
某气藏埋藏深度为3 750 m,初始水体积系数为1.003 58,地层水压缩系数为5.645×10-4MPa-1,初始孔隙压缩系数为25.013 9×10-4MPa-1,束缚水饱和度为0.32,天然气相对密度为0.568,气藏面积为47.1 km2,水区面积为9.42 km2,基于气藏实际生产数据,分别采用式(3)、(9)进行非线性回归分析,储量结果依次为 2 631×108m3、2 500×108m3(图 9),比本文参考文献[33]所述方法计算的储量(2 799.7×108m3)及容积法计算的储量(2 840.0×108m3)小;采用式(5)进行非线性回归,储量计算结果为3137×108m3,大于容积法储量,这是由于级数展开(不满足 条件)舍入误差造成的影响。该气藏后续生产情况表明容积法储量确实偏大,进一步证明了本方法的可靠性。
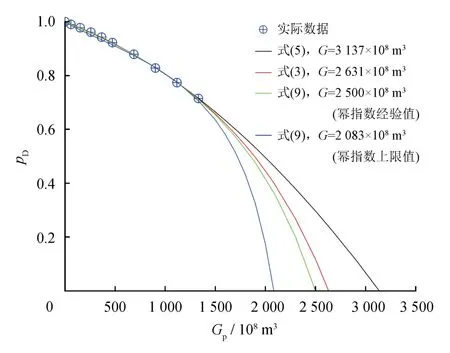
图9 高压有水气藏pD—Gp非线性回归拟合曲线图
2.2 裂缝性应力敏感气藏计算实例
对于裂缝性应力敏感气藏,由于裂缝压缩系数难以确定,亦可用本文方法进行天然气储量评价。算例选自本文参考文献[34],基质束缚水饱和度为0.25,裂缝含水饱和度为0,水相压缩系数为4.35×10-4MPa-1,基质压缩系数为2.90×10-3MPa-1,裂缝孔隙度为0.01,裂缝储容比为0.5。基于气藏实际生产数据,分别采用式(3)、(5)、(9)进行非线性回归分析,储量结果依次为45.6×108m3,46.7×108m3和45.3×108m3,与本文参考文献[34]中储量计算结果48.14×108m3接近;若忽略裂缝压缩系数的影响,对前面4个数据点进行线性回归并外推,得到天然气储量为58.3×108m3,导致天然气储量计算值过高[34](图10)。如图11所示,当视储层压力衰竭程度大于0.35后,采用式(9)计算的储量结果则较接近,此临界点与前述统计结果0.33基本一致。

图10 裂缝性应力敏感气藏pD—Gp回归拟合曲线图
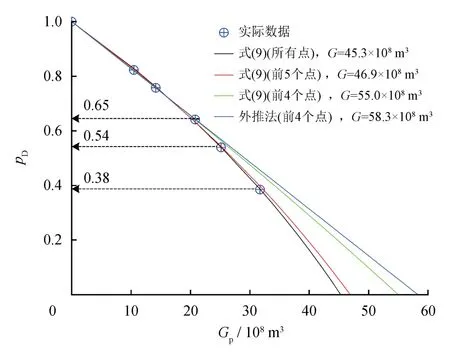
图11 视储层压力衰竭程度敏感性分析图
3 结论
1)结合国外20个已开发高压、超高压实例气藏,确定幂函数形式物质平衡方法的幂指数经验值为1.028 47,其上限值为1.115 67。
2)经典二段式拐点对应的视储层压力衰竭程度介于0.14~0.38,平均为0.23;第二直线段外推点对应的视储层压力衰竭程度介于0.23~0.50,平均为0.33;对应的采出程度介于33%~65%,平均为45%。
3)采用本文方法计算天然气储量,当视储层压力衰竭程度大于0.33时,储量计算结果误差小于10%。
4)针对高压、超高压及裂缝性应力敏感气藏,本文提出的幂函数形式物质平衡方法计算天然气储量时避开了储层岩石有效压缩系数、含水层体积及水侵量等不确定性参数,具有计算过程简单、实用性较好的优势。
