输气管道环焊缝表面裂纹管道极限载荷计算方法
2019-05-13王旭帅健
王 旭 帅 健
中国石油大学(北京)安全与海洋工程学院
0 引言
有关统计资料显示,自2010年以来我国至少发生了管道环焊缝失效事故12起,其中强力组对、焊接缺陷和材料韧性不达标是造成环焊缝失效的主要原因。因此针对在役含缺陷管道特别是环焊缝缺陷的适用性评估是一项必要且十分迫切的工作,既能从事故源头减少管道事故的发生,也能充分发挥管材性能,避免不必要的开挖、换管等开支[1]。
失效评定图方法(Failure Assessment Diagram,FAD)作为目前评估管道缺陷的主流方法之一,最早由英国中央电力局(Central Electricity Generating Board,CEGB)提出[2],而后由美国电力研究所(Electric Power Research Institute,EPRI) 提 出的“含缺陷油气容器及管道的完整性评定规程”(简称EPRI评定规程)进一步完善[3]。EPRI提出的管道缺陷的J积分估算方法及相应的J积分理论提高了FAD评估方法的实用性及准确性,对于小口径及低强度钢管具有较好的覆盖性及适用性。Lei和Budden[4]最早基于等效应力—应变的思想,结合EPRI方法,提出了考虑焊缝非等匹配下的平板中心裂纹J积分估算公式,并通过试验与有限元的方式对公式进行修正。Kim等[5-6]基于EPRI方法考虑内压和弯曲载荷情况下,给出了一定范围内的管道和裂纹几何尺寸的全塑性J积分解,进而给出了极限载荷的计算方法。Song等[7]提供了中心贯穿表面裂纹板的错匹配极限载荷以及J积分估算方法。Hertelé等[8]针对焊缝结构的材料不均匀性,提出了基于中心裂纹拉伸试件的非均匀焊缝的修正J积分计算方法。Paredes和Ruggieri[9]扩展了EPRI手册中J积分全塑性解的适用范围。Souza和Ruggieri[10]基于EPRI和参考应力法,研究了一定范围裂纹几何尺寸、焊接失配程度下的弯曲载荷作用下管道环向表面裂纹J积分的求解方法。国内学者帅健和辛艳霞[11]提出了一种基于失效评定图的可靠性分析方法去确定油气管道弹塑性断裂失效概率。孙亮等[12]在EPRI理论的基础上,导出以等效原场应力为参量的塑性J积分计算方法,白永强等[13-14]扩展了EPRI手册的适用范围等。
综上所述,含缺陷结构的塑性J积分作为管道缺陷评估方法中的关键参数,国内外学者针对其塑性解已有一定的研究基础,但是现阶段这些国内外研究成果针对目前主流的大口径、薄壁、高钢级的管道研究应用尚有不足,公式适用范围有限抑或是预测结果过于保守或激进,笔者基于目前国内已规模化应用的X80级钢管材料性能,考虑裂纹尖端处的应力奇异性,利用有限元软件ANSYS建立了含表面裂纹的管道环焊缝有限元模型,在EPRI方法的基础上考虑焊缝匹配系数的影响,研究环焊缝表面裂纹驱动力J积分的计算方法,并在此基础上分析含裂纹管道的极限载荷影响因素,可为现役管道的安全评价及完整性管理提供参考。
1 含表面裂纹的管道有限元模型
1.1 几何模型及参数
在工程实际问题中,管道环焊缝缺陷在承受轴向拉伸载荷时最为危险,本文建模即考虑此种情况,即建立受拉伸载荷作用下的含环向表面裂纹的管道模型,如图1所示。
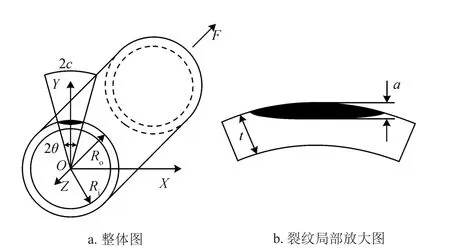
图1 含环向裂纹的管道受拉伸载荷的几何模型图
建模参数参考GB/T 9711—2017《石油天然气工业管线输送系统用钢管》[15]中关于X80级钢管的拉伸试验要求,设计系数取0.72,按GB 50251—2015《输气管道工程设计规范》[16]的壁厚公式计算壁厚,具体信息如表1所示。

表1 管道模型的尺寸及材料参数表
1.2 有限元模型
采用二维奇异单元经裂纹路径扫掠生成三维奇异单元的方法,考虑裂纹尖端的奇异性,进而构建管道环向的外表面半椭圆裂纹。即采用ANSYS推荐的PLANE183单元生成裂尖单元面,用SOLID186单元通过扫掠形成整个裂纹前缘。为减小计算量,提高计算精度,同时考虑到管道模型具有对称性,故采用1/4模型进行建模,对裂纹区域网格进行加密处理,同时远离裂纹区域适当稀疏,建立的1/4含环向表面裂纹的管道模型如图2所示。
为了研究裂纹深度和长度以及管材应变硬化性能对裂纹驱动力的影响,采用3种不同硬化指数的管材进行建模,计算了3种不同长度及深度的缺陷对裂纹J积分的影响。同时将1/4管道模型长度设为500 mm,以减少端部效应对计算结果造成的影响[17]。
1.3 模型验证
为验证所建立含缺陷管道模型计算结果的准确性,将模型计算得到的J积分通过公式(平面应力)转换为应力强度因子(KI),从而与标准中提供的KI进行对比。英国标准协会(British Standards Institution,BSI)发布的BS 7910-2015 《金属结构缺陷验收评定方法导则》中给出了管道外表面环向裂纹的应力强度因子求解方法[18]:

式中pm表示薄膜应力,MPa;pb表示弯曲应力,MPa;M表示焊缝匹配系数;其余符号均为无量纲的计算参量,可通过查附录得其表达式或数值,其中下标为b的代表弯曲应力相关参量,本文计算中均取0。
图3为在轴向拉伸载荷作用下即pm=0.6σ0(σ0表示屈服强度,取表1数据),多组不同缺陷尺寸下的管道环向裂纹最深处应力强度因子计算值的对比情况。经计算误差均在5%以内,说明所建立的含环向表面裂纹的管道有限元模型计算结果较为准确可信。
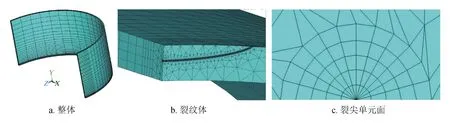
图2 有限元模型图
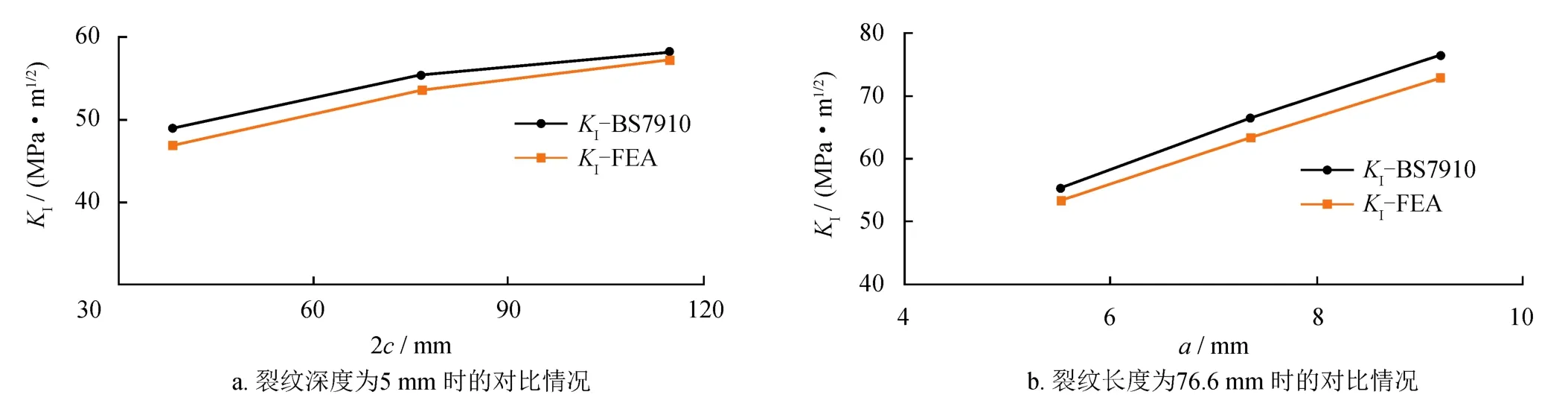
图3 有限元计算的KI值与BS 7910标准中的KI值比较图
2 环焊缝表面裂纹因子
EPRI方法将J积分的计算分为弹性部分Je和塑性部分Jp。其中,弹性部分Je可由式(平面应力情况下)得到。塑性部分表达式为:
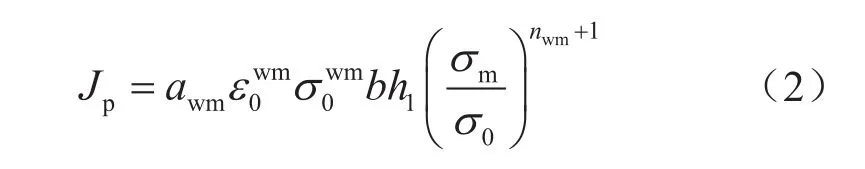
式中b表示非裂纹部分的尺寸,mm,b=t-a;σm表示管道远端施加的拉伸载荷,MPa;σ0表示屈服强度,MPa;ε0表示σ0对应的应变;h1表示无量纲因子;其余带wm上标或下标的符号表示焊接金属(Weld Metal)的对应性质。
由式(2)可以看出,h1因子为EPRI方法估算J积分的关键参数之一,其数值与管道环焊缝表面裂纹尺寸以及管材应变硬化性能有关。由式(2)可得:
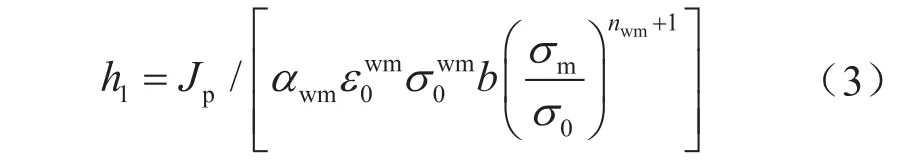

其中 JP_FE=J-Je。
2.2 考虑焊缝匹配系数的有限元模型
为研究管道环焊缝的焊缝匹配系数对含缺陷管道的影响,考虑选用两种较为明显的焊缝强度错匹配情况:20%的低匹配(指焊缝的屈服强度比母材屈服强度低20%,M=0.8)和20%的高匹配(指焊缝的屈服强度比母材屈服强度高20%,M=1.2)。并在此基础上对前述的有限元模型进行材料设置。参考本文参考文献[19]对X80级钢管的材料性能研究,采用R-O模型来描述材料的应力应变性能,将有限元模型的管道材料设置如表2所示,表中n值为R-O模型的参数,代表材料的幂硬化指数。

表2 含环焊缝裂纹缺陷的管道模型材料设置表

图4 不同匹配情况下的环焊缝h1因子随裂纹尺寸的变化图
基于考虑焊缝匹配系数的有限元模型以及上述式(4)即可实现对不同情况下的h1因子进行求解。考虑不同的焊缝匹配系数及不同裂纹尺寸情况,将所得结果绘制如图4所示。
由图4的结果总体来看,h1因子随着裂纹的长度、深度以及材料硬化指数及焊缝匹配系数的增大而增加,匹配系数越高,h1因子对裂纹的尺寸越敏感;而裂纹尺寸较大时,材料硬化指数对h1因子影响也越来越明显。根据h1因子随裂纹的长度及深度的变化情况,可将h1因子描述为裂纹尺寸的函数,裂纹长度和深度分别用来表示,采用多元多项式进行拟合,即
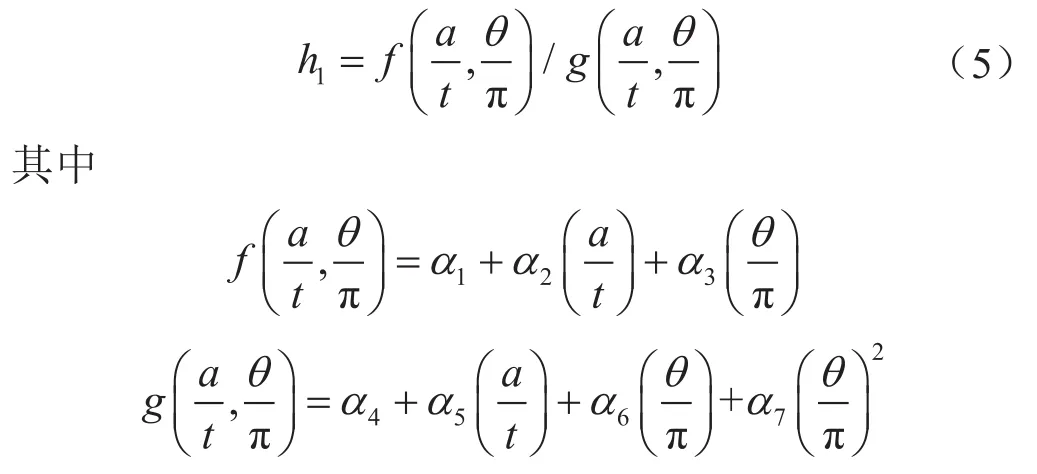
式中α1~α7表示参数,其值采用非线性最小二乘法莱文贝格-马夸特法(Levenberg-Marquardt Method)拟合得到,列于表3中,适用范围为0.01≤0.03、0.3≤0.5。
根据表3参数及式(5)拟合出h1因子函数,与有限元计算得到的h1因子值进行对比,计算所得误差情况如图5所示。可以看出低匹配和等匹配情况下部分误差较大,在M=0.8、n=14时,出现最大的拟合误差在14%左右,但是整体平均误差在5%以内,说明本文拟合的适用于X80管道的环焊缝表面裂纹J积分计算公式具有较高的精度,能够实现较大裂纹尺寸范围、且考虑焊缝匹配系数的含管道环焊缝裂纹J积分运算,满足工程计算的需要。
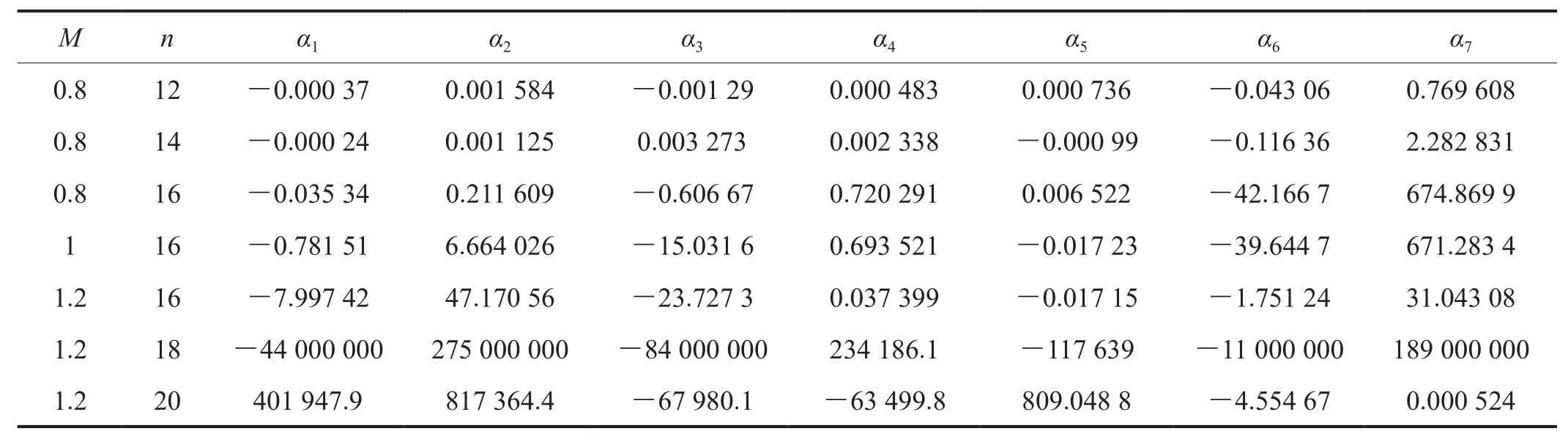
表3 h1因子多项式拟合的参数值表

图5 h1因子拟合误差图
3 基于J积分的极限载荷分析
基于塑性全量理论发展的塑性极限载荷分析理论目前已成为多个标准计算含环向裂纹管道的极限载荷的主要推荐方法之一,其中应用最为广泛的是净截面垮塌准则,该准则假设含环向裂纹的管道处于塑性极限状态时,管道承受载荷发生变形时的裂纹净截面上的应力为均布的屈服应力[20],塑性极限载荷反映了含缺陷管道的极限承载能力。BS 7910中将含缺陷管道极限载荷定义为:
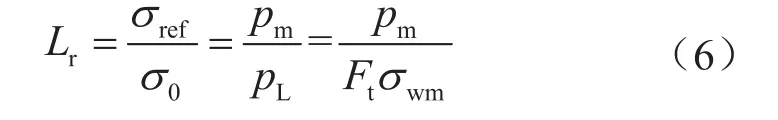
式中Lr表示载荷比;pL表示管道轴向极限载荷,MPa;Ft表示极限载荷系数;σwm表示焊缝材料的屈服强度,MPa;σref表示参考应力,其大小与缺陷位置及尺寸有关,MPa。
上式中Lr应满足:
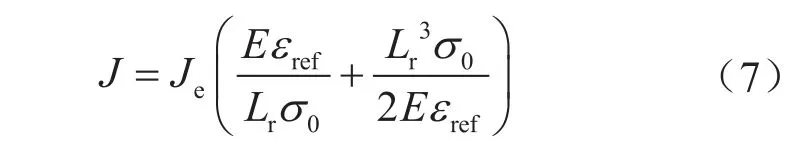
式中εref表示参考应变,其数值等于真应力为参考应力 σref=Lrσ0时对应的真应变。
由式(6)、(7)结合上述建立的有限元模型,即可求得任意载荷作用下的J和Je,进而求得对应载荷作用下的Lr,具体求解过程本文不再赘述,现将不同匹配强度下的含缺陷管道极限载荷计算情况绘制如图6所示。
由图6可以看出,在低匹配、等匹配或高匹配情况下,含缺陷管道的极限载荷均随着裂纹尺寸的增加而降低,随着材料硬化指数的增大而增大;而在管道裂纹缺陷尺寸及材料硬化指数一定时,高匹配的含缺陷管道的极限载荷明显要高于低匹配或等匹配的情况,某些情况下高匹配的含缺陷管道的极限载荷甚至要高于管道母材本身的屈服极限载荷。说明对含环焊缝中心线处表面裂纹的X80管道而言,高强匹配是明显优于低匹配的。

图6 不同匹配情况下的含缺陷管道的极限载荷图
根据含缺陷管道的极限载荷的随裂纹尺寸、材料硬化系数、匹配强度等参数的变化情况,现根据式(6)求出极限载荷系数(Ft),并将其转变为裂纹深度和长度的函数,采用多项式进行拟合,即可在特定强度匹配水平和材料应变硬化性能的情况下快速求出含缺陷管道的极限载荷,Ft系数的表达式为:

其中
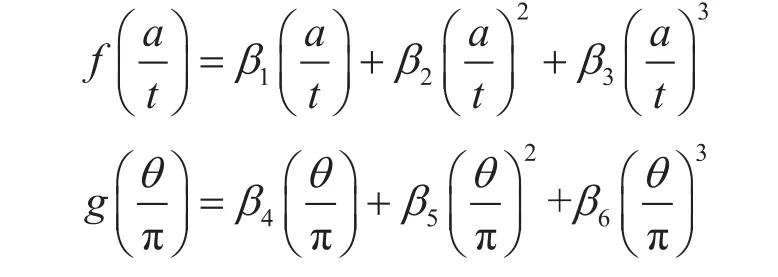
式中β0~β6表示参数,其值采用非线性最小二乘法莱文贝格-马夸特法(Levenberg-Marquardt Method)进行拟合而得,将得到的参数列于表4,本公式的适用范围为。
据式(8)及拟合系数即可快速计算含缺陷管道的极限载荷,并与有限元结果进行对比,拟合公式的计算误差见图7,从中可以看出无论最大误差还是平均误差均没有超过0.5%。故认为本文拟合的含缺陷管道极限载荷计算公式具有较高的精度,能够满足工程计算的需求,实现考虑焊缝匹配系数及材料硬化指数的含环焊缝缺陷管道的极限载荷快速计算。
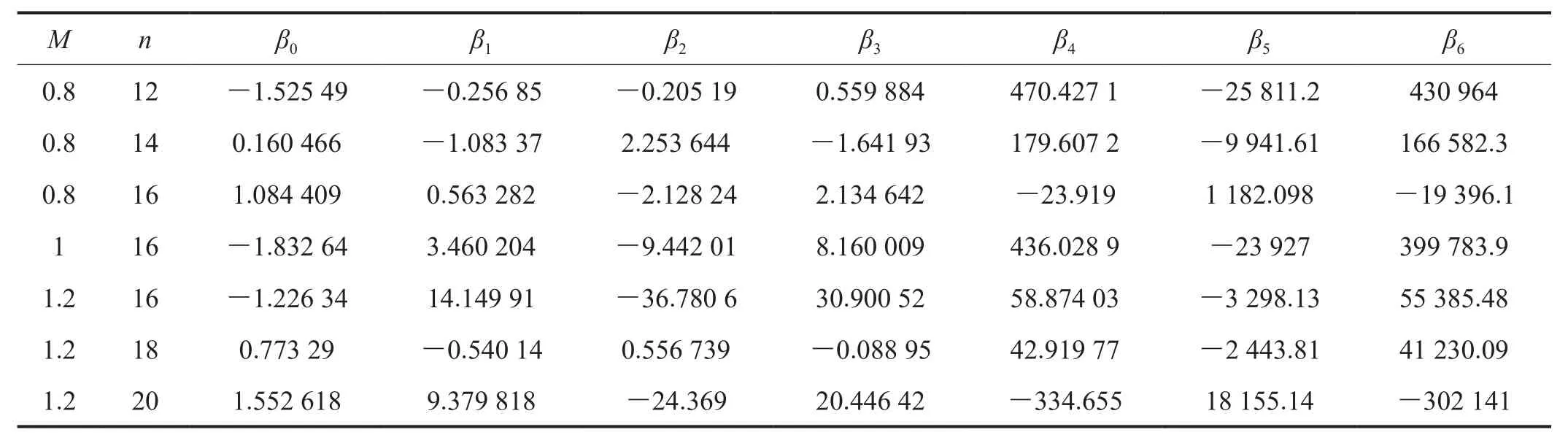
表4 Ft系数多项式拟合的参数值表

图7 Ft系数的拟合误差图
4 结论
1)建立了含环向表面裂纹的管道有限元模型,与BS 7910中提供的应力强度因子值的对比误差均在5%以内,说明所建立的含环向表面裂纹的管道有限元模型计算结果较为准确可信。
2)含缺陷管道的裂纹J积分会随着裂纹的长度、深度以及材料的硬化指数(n)、焊缝匹配系数(M)的增加而增加;M越大,J积分对裂纹的尺寸越敏感;而裂纹尺寸较大时,材料的n对J积分的影响也越来越明显。
3)在低匹配、等匹配或高匹配情况下,含缺陷管道的极限载荷会随着裂纹尺寸的增加而降低,随着材料硬化指数的增大而增大;而在管道裂纹缺陷尺寸及材料硬化指数一定时,高匹配的含缺陷管道的极限载荷明显要高于低匹配或等匹配的情况,说明对含环焊缝中心线处表面裂纹的X80管道而言,高强匹配是明显优于低匹配的。
4)在对含缺陷管道J积分及极限载荷影响因素分析的基础上,提出了针对特定匹配系数和材料硬化指数情况下的,能够实现J积分及极限载荷快速计算的公式,与有限元计算结果对比表明,公式计算结果具备较高的精度,可以满足工程计算需要。
