数字样机技术在升船机主提升减速器设计中的应用

王 海 洪 雷 李学明

(二重(德阳)重型装备有限公司，四川610000)

升船机是一种重要的河道通航设备。在垂直卷扬式升船机提升系统中，主提升减速器作为核心部件，将电动机输出转矩降速增矩后，驱动卷扬卷筒正反转，实现乘船厢的升降。此类减速器通常具有速比大、输出转矩大和安全性要求高等特点，是一种典型低速重载传动型式。以亭子口2×500 t升船机为例：主提升减速器速比为618.7，输出转速1.2 rmin，而输出转矩高达2×650 kN·m。

重载齿轮传动由于传递转矩大，齿轮啮合时齿面接触应力高，一般采用渗碳淬火硬齿面齿轮传动[1]，对齿轮硬化层深度，以及齿部应力分布和接触斑要求严格。如果不进行齿部修形和适当的硬化层深设计，很容易发生齿部偏载、振动超标和接触失效等问题，严重影响齿轮箱的工作性能和服役寿命。

减速器内部轴系弯曲、扭转变形，以及箱体柔性等因素都会导致齿面接触位置变化，一般理论算法很难精确计算齿面实际接触情况。为了准确地进行齿面微观形态修正和计算渗碳层深度，结合亭子口升船机SCJ-1650型主提升减速器的设计，建立了减速器的数字化样机模型。在此基础上，综合考虑工作载荷作用下箱体及轴系的变形等影响，准确计算各级齿轮副的啮合错位量、传动误差和最大剪应力深度，为齿面微观形态修正和渗碳层深度的确定提供依据。

1 数字样机模型的建立

SCJ-1650型主提升减速器采用表面硬化齿轮，分四级传动，主要性能参数见表1。其中第一级、第二级和第四级采用平行轴圆柱齿轮传动，第三级采用人字齿轮传动，齿轮与轴之间采用过盈配合和键联接方式，所有齿轮均为渗碳淬火齿轮，齿面硬度58～62HRC，表面粗糙度Ra0.8 μm。

针对上述升船机主提升减速器，应用Romax Designer专业齿轮箱分析工具，建立了图1所示的数字化样机模型[2]。图1(a)为齿轮箱传动链系统，包括各级齿轮传动副、轴和轴承，其中包含了各个轴系的静力学和动力学模型，对传动链系统施加输入载荷后，可以用于齿轮、轴和轴承的寿命校核。此时各轴系的受力变形等的计算是假想各个轴承外圈为刚性固定的。通过导入箱体的有限元模型，再通过约束轴承外圈与箱体连接，那么，就可以建立一个完整的减速器数字样机模型，此模型包含柔性化箱体，如图1(b)所示。柔性化箱体模型与传动链进行耦合后，可以考虑箱体变形对齿轮啮合的影响，更加准确地分析齿轮啮合时齿面的微观接触形态。

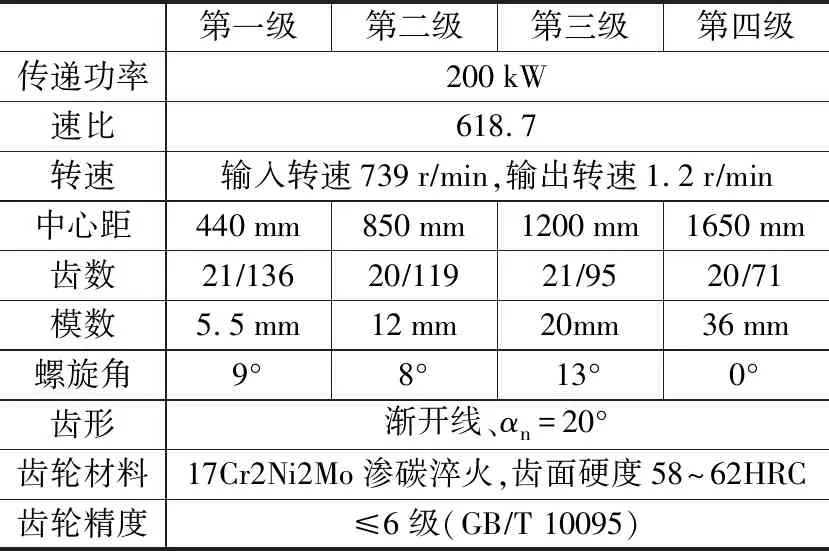
表 1 SCJ-1650主要性能参数

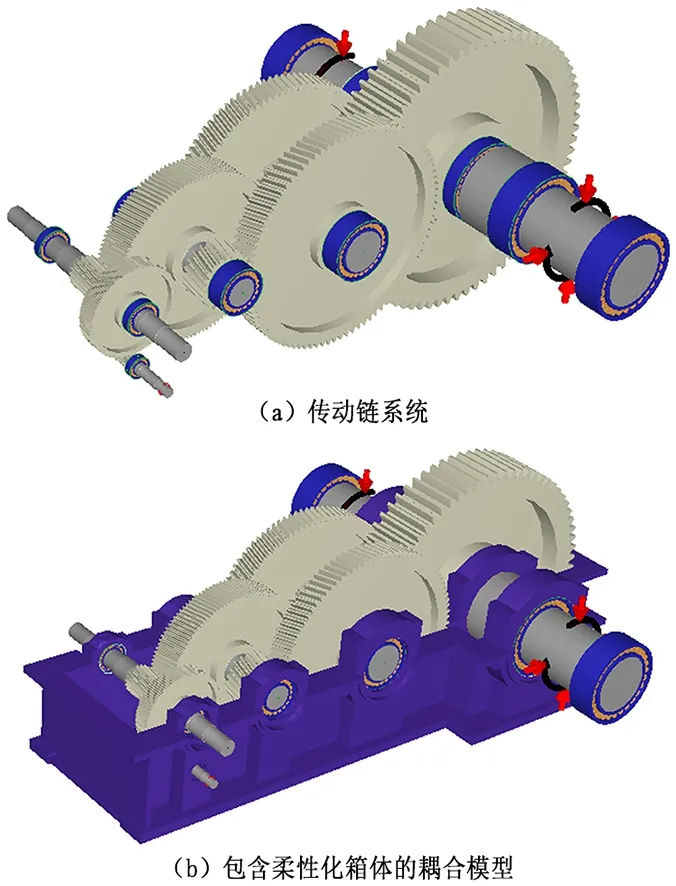
图1 减速器数字化样机模型

2 齿面微观形态修正

齿轮齿面微观形态修正主要包括齿向修形和齿廓修形。齿向修形主要用来弥补由于轴系扭转变形造成的齿长偏载影响，一般包括齿线修斜、两端局部过切，以及齿线起鼓。齿线修斜以抵消齿轮啮合错位；两端局部过切(修端)，防止齿端局部过载；齿线起鼓使齿面载荷由齿长中部向外递减分布。齿廓修形主要用来补偿轮齿弯曲变形造成的啮合误差，其修形量的设计依据是轮齿的啮合弯曲变形量。齿顶、齿根一般采取近似对称的修形长度，未修形部分的齿廓端面重合度不小于1.1～1.2。经过修形的齿轮，其工作性能与载荷的大小有关，因此修形齿轮在工作载荷相对稳定的情况下采用效果较突出。

齿轮修形时一般采用以下的计算载荷：

修形计算功率(或转矩)=(0.7～0.8)×工作机械的实际计算功率(或转矩)

载荷折算系数(KAKVKHβKHα)=1

即按工作机械的实际工作功率的70%～80%直接作为齿轮修形时的计算载荷。十分理想的齿轮修形结果应是：除使用系数KA以外的各项载荷修正系数均为1，也就KVKHβKHα=1，不存在内部冲击与载荷不均匀的理想情况(事实上很难实现)。上式中的(0.7～0.8)主要考虑未满载时反而会不利的情况。

基于建立的减速器数字样机模型，在给定输入工况后，通过定量计算齿轮啮合错位及传动误差，对齿面进行齿廓及齿向修形。以第二级齿轮传动副为例，图2给出了小齿轮齿面修形方案。

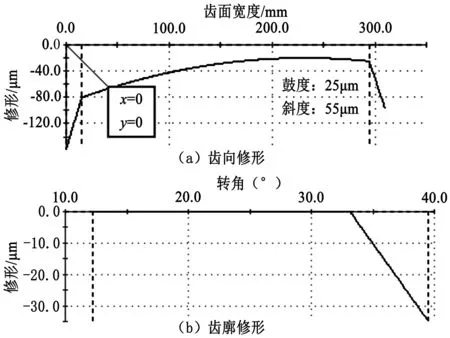
图2 第二级小齿轮齿面修形方案Figure 2 Tooth surface modification scheme for the second stage of pinion

齿廓修形对传动性能的影响主要体现在传动误差的变化量上，修形前后传动误差的变化见图2。齿长修形主要影响齿面的接触应力分布，图3给出了第二级传动齿轮副修形前后小齿轮齿面应力分布的变化。从图中可以看出，修形前，齿面最大接触应力位于轮齿端部，载荷分布不均匀；修形后最大接触应力位于轮齿中部，向两端递减均匀分布，且最大接触应力降低237 MPa。

从表2中可以看出，通过齿面修形，各级传动误差变化量明显减少，齿面接触应力分布得到明显改善，最大接触应力也相应有所降低。通过齿面微观形态修正，有效地提高了传动平稳性，减少了由轮齿受载变形引起的啮合初始冲击，改善了齿面的润滑状态，并获得了较为均匀的齿面载荷分布。KHβ系数主要考虑齿向载荷分布不均匀对齿轮计算寿命影响。

3 齿轮渗碳层深度

为了防止渗碳齿轮硬化层的剥落，有效硬化层深度应不小于最大剪应力深度的1.5倍。出于安全性等考虑，一般规定齿廓中点处的有效硬化层深度不小于节点处最大剪应力深度的2倍[3]。正常工艺条件下，齿廓的硬化层深度从齿顶到齿根平缓过渡(减小)，齿根处的渗碳层深度一般不小于齿廓中点渗碳层深度的80%。

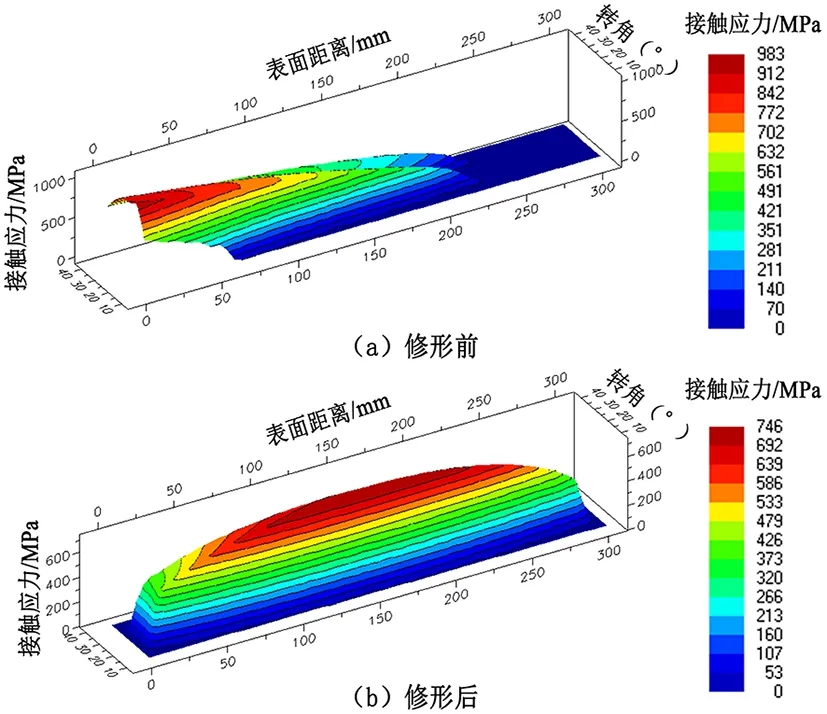
图3 第二级小齿轮齿面修形前后接触应力分布

传动误差变化量∕μm齿向载荷分布系数KHβ齿面最大接触应力∕MPa修形前修形后修形前修形后修形前修形后第一级第二级第三级第四级2625450.92.23.55.52.362.8863.1191.2061.471.5081.3761.15310119831109951875746791959

轮齿接触区的最大剪应力深度hr与接触应力σH、齿廓接触点的当量曲率半径ρ有关，按轮齿弯曲与接触等强度条件确定的齿轮法向模数mn可以与最大剪应力深度hr建立近似的线性关系，如果所选模数能够满足弯曲强度安全系数不低于接触强度的安全系数，则可以大致推算出最大剪应力深度的范围[4-5]，按这种方法确定渗碳层深度的精确性不是很高。

如图4所示，通过所建立的减速器数字样机模型，可以计算得到各级齿轮啮合时小齿轮齿面剪应力及其深度分布。按照计算得到的各级齿轮啮合时的最大剪应力深度，考虑安全裕度，取安全系数3，计算得到渗碳层深度tH1见表3。根据ISO标准，按照优先保证接触强度，计算得到的渗碳层深度tH2，列于表3中以作对比。从表3中可以看出，对于模数30以下的中小模数齿轮，通过模型精确计算得到的渗碳层深度与按照ISO标准计算得到的渗碳层深度较为接近，同时也验证了基于数字样机技术来确定齿面渗碳层深度的可行性。

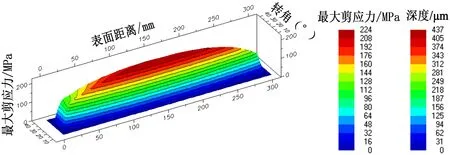
图4 第二级小齿轮齿面剪应力与深度分布Figure 4 Shear stress on tooth surface and depth distribution of the second stage of pinion

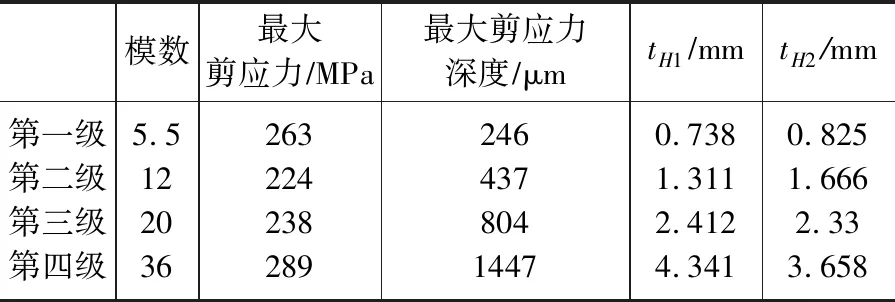
模数最大剪应力∕MPa最大剪应力深度∕μmtH1 ∕mmtH2∕mm第一级第二级第三级第四级5.512203626322423828924643780414470.7381.3112.4124.3410.8251.6662.333.658

4 结论

通过建立升船机主提升减速器的数字化样机模型，施加适当工作载荷，确定齿轮箱在工作时箱体及轴系的变形量，从而精确计算各级齿轮啮合时的啮合错位及传动误差，对齿面的微观形态进行修正。从结果可以看出，齿面的微观修形较好地改善了齿面载荷分布，减少了传动误差，提高了齿轮的承载能力和传动平稳性。同时，通过精确计算齿面剪应力及其深度分布，确定了齿轮表面硬化层深度。

渗碳淬火硬齿面齿轮如何进行正确的齿面微观形态修正以及保证有效的渗碳淬火层深度，将直接影响到齿轮传动的性能和使用寿命。文中所述主提升减速器，通过建立数字样机模型确定各级齿轮的齿面微观形态和渗碳层深度后，在亭子口2×500 t升船机主提升机上使用效果良好。实践表明，通过建立减速器数字样机模型，并施加适当的载荷工况进行模拟，为齿轮副齿面微观形态修正以及渗碳层深度的确定提供了一种行之有效的方法。