An Influence Maximization Algorithm Based on the Mixed Importance of Nodes

Yong HuaBolun Chen ∗ Yan YuanGuochang Zhuand Jialin Ma

Abstract:The influence maximization is the problem of finding k seed nodes that maximize the scope of influence in a social network.Therefore,the comprehensive influence of node needs to be considered,when we choose the most influential node set consisted of k seed nodes.On account of the traditional methods used to measure the influence of nodes,such as degree centrality,betweenness centrality and closeness centrality,consider only a single aspect of the influence of node,so the influence measured by traditional methods mentioned above of node is not accurate.In this paper,we obtain the following result through experimental analysis:the influence of a node is relevant not only to its degree and coreness,but also to the degree and coreness of the n-order neighbor nodes.Hence,we propose a algorithm based on the mixed importance of nodes to measure the comprehensive influence of node, and the algorithm we proposed is simple and efficient.In addition,the performance of the algorithm we proposed is better than that of traditional influence maximization algorithms.

Keywords:Influence Maximization,social network,mixed importance,coreness.

1 Introduction

With the prosperous development of social network in recent years,the research on social network has attracted attention of many scholars.The social network,such as facebook,twitter and blogs,is composed of social relationships among individuals,as a result the potential business value of social network is enormous.One of the classical applications in social network is viral marketing,in generally,using the ‘word of mouth’effect[Guille(2013);Goldenberg,Libai and Muller(2001)]to market products online.For instance,a software company plans to sell a software through network.The salesman of the software company will look forkinfluential initial users and pay thekinitial users rewards in the social network.Then,thekinitial users promote the software to their acquaintances.The social relationships among acquaintances become the key of viral marketing,because acquaintances are more convinced than strangers[Hill,Provost and Volinsky(2006);Sadovykh,Sundaram and Piramuthu(2015);Schmitt,Skiera and Den Bulte(2011);Verbraken,Goethals,Verbeke et al.(2014);Iyengar,Den Bulte and Valente(2011)].Therefore,the scope of promotion of the software will be expanded through the ’word of mouth’effect.As described in the previous example,the problem above is called the influence maximization problem[Domingos and Richardson(2001)],whose essential problem is how to find the most influential initialkusers.

The problem of influence maximization was first proposed by Kempe et al.[Kempe,Kleinberg and Tardos(2003)].They demonstrated that finding the subset of nodes with optimal influence in social network is an NP-hard problem and a approximate guarantee of optimal solution is obtained by using the simple greedy algorithm.In addition,they put forward using independent cascading model or linear threshold model to simulate the propagation of information in discrete time in social network.The key of selecting influential initialkusers in the influence maximization is how to measure the ability of spreading influence of node.A variety of central methods,such as degree centrality,betweenness centrality and closeness centrality,were proposed in the original study of the problem of influence maximization.The ability of node to spread the influence in a social network can be measured directly through the methods above.In the subsequent research in the problem of influence maximization,the property of the submodular function[Nemhauser,Wolsey and Fisher(1978)]was used in many greedy algorithms to approximate the optimal solution through extensive iterations.Chen et al.[Chen,Wang and Yang(2009)]proposed a degree discount heuristic algorithm,compared with CELF algorithm proposed in Leskovec et al.[Leskovec,Krause,Guestrin et al.(2007)],which greatly reduces the time complexity and makes the seed set choosed by this algorithm having more influence.Lee et al.[Lee and Chung(2014)]proposed a 2-hop greedy algorithm based on the phenomenon that the influence of node reach most nodes needing only 2-hop,whose time complexity is less than CELF++and achieves a more influential seed set[Goyal,Lu and Lakshmanan(2011)].Chen et al.[Chen,Wang and Wang(2010)]proposed PMIA algorithm,which uses MIIA(maximum influence in-arborescence)and MIOA(maximum influence out-arborescence)to model the influence of node.The PMIA algorithm has a lower time complexity than the simple greedy algorithm,but the space complexity of PMIA is higher than the simple greedy algorithm,because PMIA needs to build influence propagation tree for each node.Jung et al.[Jung,Heo and Chen(2012)]proposed a novel algorithm IRIE,which combines the influence ranking algorithm and the influence estimation algorithm,andachieved lower timecomplexity and moreefficient than PMIA.Many novel algorithms with excellent results in measuring the influence of node have been proposed in recent studies.Kitsak et al.[Kitsak,Gallos,Havlin et al.(2010)]found that the most effective influence spreaders are often not the nodes with large degrees,but the nodes are in the core location of the social network.The correlation between the coreness and the propagation ability of node in the social network was analyzed by k-shell decomposition[Carmi,Havlin,Kirkpatrick et al.(2007)],which provided a new solution to the problem of influence maximization.Gao et al.[Gao,Ma,Chen et al.(2014)]presented that the influence of node is related to their local structure.A algorithm based on local structure centrality,which uses the topology and centrality of node and its neighbors to measure the ability of spreading influence of node,was proposed.This algorithm is more accurate than the previous algorithm when evaluating the influence of node.Xia et al.[Xia,Song,Jing et al.(2018)]construct double-layer network and use markov chains theory to study disease spreading,who proposed that the scale of disease spreading can be reduced by increasing the rate of spreading.

In real social network,the larger degrees a node has,the more likely it is to be chosen as a initial node.However,the ability of a node to spread influence is related not only to the degree of node and its neighbors,but also the coreness of node and its neighbors.In other words,the ability of a node to spread influence is also related to the degree and coreness of its neighbors.In this paper,we study the correlation between the mixed importance and the ability of node to spread influence,and we propose an influence maximization algorithm based on the mixed importance of nodes.In contrast to the traditional algorithms,we consider the cost of selecting initial nodes in social network.Moreover,our algorithm is more adaptive[Zhang,Zheng and Xia(2018)]and achieves good performance.

2 Description of the problem

2.1 Influence maximization problem

We define a undirected social networkG=(V,E),whereVrepresents the node set in social networkG,andErepresents the collection of edges between nodes.Moreover,n=|V|,wherenis the total number of nodes in social networkG.If nodeuandvexist in the social networkG,we use(u,v)∈Eto represent an edge between theuandv,and usepto represent a propagation probability.We usemto represent the total number of edges in social networkG.The influence maximization problem is to find the subset of node set in the graphG,which is a set composed of seed nodes.We useSto represent seed set,k=|S|.In addition,the influence of thekseed nodes is maximum.

2.2 Independent cascade model

We use the independent cascade model to simulate the influence of node and measure the ability of node to spread influence[Chen,Fan,Li et al.(2015);Liu,Cong,Xu et al.(2012)].The principle of the independent cascade model is as follows:in the networkG,all nodes have only two states:active or inactive.Aiis the set of nodes activated at timei.The initial phase is the timet=0.A0=Srepresents that the nodes in the seed setSare active and other nodes are inactive at timet=0.At timet=i,u∈Ai-1and the nodevis in the inactive state.uattempts to activate nodevwith propagation probabilitypfor edge(u,v)∈E.Ifvis successfully activated,vmaintains activated state fromt=i+1.Ifvfails to be activated byu,vcan not be activated byuat a later time.If nodevhas multiple neighbors that have already been activated,the neighbors ofvwill activatevwith a probability of1-(1-p)l,wherelis the number of neighbors that have been activated.WhenAiis empty,that is,at timet=i,no nodes are activated,the propagation process ends,and the number of activated nodes in the whole process represents the influence of the seed setS[Kim,Kim,Oh et al.(2017);Kimura,Saito,Nakano et al.(2010)].

2.3 Influence function

We denote the influence function asinfluence(·),where the functioninfluence(·)maps a subset of the node setVto a nonnegative integer.For example,influence(u)is the number of node activated by nodeu,andinfluence(S)is the number of node activated by seed set S.We calculate the value of functioninfluence(·)through the independent cascade model.

2.4 Cost

In the initial phase of the influence maximization problem,the initial users need to be selected as seeds,but we need to give the seeds certain rewards.In a real social network,a node with a greater degree has a wider social range.Therefore,a node with large degrees will be given more rewards than a node with small degrees.In this paper,we define the initial cost by Eq.(1),wheredegreeuis the degree of nodeuand the functionmean(·)is the average function.

3 Detailed process of the algorithm

In this paper,we use the mixed importance to measure the influence of node.In the mixed importance algorithm,we consider that the influence of node affected by its norder neighbors.The obvious representation of a node affected by its neighbors is the degree of node,but only using the degree of node to measure the influence of node results in incomprehensive measurement.If nodeuandvhave the same degrees,the influence of the nodeuis better than nodev,when the number of 2-order neighbors of nodeuis more than nodev.Furthermore,if nodeuand nodevhave the same degrees,but nodeuand its neighbors are in the core location of social network,the ability of the nodeuto spread influence may be better.Many scholars have put forward that the influence of node is limited.Therefore,we limit the propagation scope of node to the 2-order neighbors,ignoring the rest of neighbors,that is,we measure the influence of node by using the mixed importance of the degree and the coreness of the node’s 1-order and 2-order neighbors.The mixed importance algorithm show in Tab.1.

The input of the mixed importance algorithm is social networkG=(V,E)and the number of seed nodesk.The output of this algorithm is the seed setS.By traversing the values ofαandβ,the mixed importance algorithm calculates the mixed importance of node in differentαandβ.The optimal values ofαandβ,that isαbestandβbest,are obtained and put into Eq.(2)by calculating the kendall correaltion coefficients.Then,the mixed importance values of all nodes are calculated,andknodes with the maximum mixed importance values are selected as the seed nodes.Among the mixed importance algorithm,Step 1 is the input of algorithm:the number of social networkG=(V,E)and the number of seed nodesk.In Steps 2 and 3,letαandβcycle from 0.1 to 0.9 with an increase of 0.1 per iteration.The key steps are described detailedly in the following subsections.

Table1:Mixed importance algorithm

3.1 Mixed importance

Step 5 calculates the mixed importance valueMI(v)of the nodev.In the social networkG,we set the 1-order neighbor node set of the nodeuto Γ1,wheredu=|Γ1|andduare the number of the 1-order neighbors of the nodeu,which is also the degree of nodeu.We set the set of 2-order neighbor node set of nodeutoΓ2.Thus,the total number of 1-order and 2-order neighbors of nodeuisNe(u)=|Γ1∪Γ2|.We set the coreness of nodeutoCore(u).The coreness of nodeuis small,when nodeuis at the edge of network.The coreness of nodeuis high,when nodeuis at the core location of network.We define the mixed importance of node as shown in Eq.(2).

whereMI(u)is the mixed importance of nodeu,w⊂|Γ1∪Γ2|dw-Ne(u)is the total degrees of the 1-order neighbors and the 2-order neighbors of nodeuafter nodeuis removed,andΣw⊂|Γ1∪Γ2|Core(w)is the sum of the coreness of the 1-order neighbors and the 2-order neighbors of nodeu.αis a parameter used to balance the degree and the coreness.βis a parameter used to balance the relationship between a node and its neighbors.Bothαandβare both between 0.1 and 0.9.

In Eq.(2),if the value ofαis large,it indicates that the degrees of node and its neighbors in the 2-order scope play a greater role in the influence of node.If theαvalue is small,it indicates that the coreness of node and its neighbors in the 2-order scope play a greater role in the influence of node.If the value ofβis large,it indicates that the degree and coreness of node play a greater role in the influence of node.If the value ofβis small,the degrees and coreness of neighbors in the 2-order scope of node play a greater role.

Step 6 is to simulate the influence of nodevby using the independent cascade model,and obtain the influence of nodev,influence(v).

3.2 Kendall correaltion coefficient

Step 8 is to calculate the kendall correlation coefficient under the current value ofαandβ.The kendall correlation coefficientταβ[Kendall(1938)]is described as follows:consider the joint observation pairing of two sets of random variablesXandY.Ifxi＞xjandyi＞yjorxi＜xjandyi＜yjfor the observation pairs(xi,yi)and(xj,yj),we say that the pairs are consistent.Ifxi＞xjandyi＜yjorxi＜xjandyi＞yj,we say that the pairs are inconsistent.Ifxi=xjandyi=yj,we say that the pairs are neither consistent nor inconsistent.The kendall correlation coefficient is defined by Eq.(3).

In Eq.(3),ηcandηdrepresents consistent pairs and inconsistent pairs respectively.BecauseXandYhave the same number of elements,ηrepresents the number of elements inXorY.In this paper,we calculate the mixed importanceMI(u)of every nodeuin networkGand use the independent cascade model to perform multiple influence simulations on nodeuto obtain the average value,that is,the influence valueInfluences(u)of nodeu.Therefore,setXis{MI(u)|u∈V}and setYis{Influences(u)|u∈V}.Through the calculation of kendall correlation coefficientτ,we can analyze the correlation between the mixed importance of node and the influence of node to more accurately measure the ability of node to spread influence.The value ofτis in the range of[-1,1].The value ofτis high,when the ability of node to spread influence is great and the mixed importance value of node is high.

The mixed importance value and influence of all nodes can be respectively obtained from Step 5 and Step 6,andταβis calculated by Eq.(3).Each pair ofαandβvalues corresponds to anταβvalue,and Step 11 is to select the maximumταβvalue and assigns the correspondingαandβvalues toαbestandβbest.From Steps 12 to 14,αbestandβbestare put into Eq.(2)to calculate the mixed importance value of all nodes.Finally,Step 15 selectsknodes with the maximum mixed importance value to be the seed setS.

4 Experimental results and analysis

We perform the experiments on four real social network datasets and 4 random network datasets.The four real social datasets are email[Yin,Benson,Leskovec et al.(2017)],socfbBowdoin47[Traud,Mucha and Porter(2012)],hamsterster[Dünker and Kunegis(2015)],and socfbSmith60[Traud,Kelsic,Mucha et al.(2011)].The data of Email derived from the large European research institutions and consisted of email sent and received by users.If one email at least is sent and received between useruand userv,there is an edge betweenuandv.SocfbBowdoin47 and socfbSmith60 are extracted from the data of facebook.If there is a friend relationship between useruand userv,there is an edge betweenuandv.Hamsterster is a collection of friends and loved ones from the hamsterster.com website.The four random datasets are undirected networks generated by Pajek and are denoted as random1,random2,random3,and random4.The topological attributes of all the datasets are shown in Tab.2,wherenis the total number of nodes in the dataset,mis the number of edges,dmaxis maximum degree,¯dis average degree,ris same coefficient,Cis clustering coefficient,andDis network density.

4.1 Selection of the optimal parameters

Firstly,we analyze the value ofαandβ,because the value ofαandβin the Eq.(3)is variable.Therefore we need to calculate the optimal value ofαandβin different datasets.Moreover,the value of Eq.(2),that is the value of mixed importance,is positive correlation with the influence of node,so we use kendall correlation coefficientτto measure the correlation between the mixed importance of node and the influence of node.The optimal value ofαandβis obtained when the value ofτis maximum.In the networkG,we calculate the mixed importanceMI(u)of each nodeuaccording to Eq.(2),where the range ofαandβranges from 0.1 to 0.9.We traverse the double circulation constructed byαandβ,and the value ofαorβincrease 0.1 in each circulation.Secondly,we simulate the influenceInfluences(u)of each nodeuby using the independent cascade model in each circulation.In this paper,we set the probability of propagationp=0.01in the independent cascade model.Finally,we calculateτafter the double circulation constructed byαandβ,and select the optimal value ofαandβwhen the value ofτis maximum,in detail,the value ofτis calculated by Eq.(3).

Figure1:Heat map on four real social network:we analyze the value of α and β in different real social network because α and β are unknow in Eq.(3).We study the correlation between the influence of node and the mixed importance of node by using kendall correaltion coefficient.The maximum τ in the heat map illustrate that the value of Eq.(3)with current α and β accord optimally with the real influence of node

4.1.1 Real network

In this section,we perform the mixed importance algorithm in the 4 real social networks to find the optimal value ofαandβin the every dataset respectively.In Fig.1,the vertical axis represents the value ofα,the horizontal axis represents the value ofβ,and(α,β)corresponds to the value ofτcalculated by Eq.(3).Fig.1(a)shows the result of the email dataset.wefind the value ofτis the best whenα=0.9andβ=0.5.In other words,Whenα=0.9andβ=0.5,the valueMI(u)of each nodeuis consistent with the valueInfluences(u),that is,the mixed importance value of nodeuis positive correlation with thein fluenceofnodeu.Similarly,Fig.1(b)show that thevalue ofτofthesocfbBowdoin47 dataset is the best,whenα=0.8andβ=0.7;Fig.1(c)show that the value ofτof the hamsterster dataset is the best,whenα=0.1andβ=0.1;Fig.1(d)show that the value ofτof the socfbSmith60 dataset is the best,whenα=0.8andβ=0.1.

4.1.2 Random network

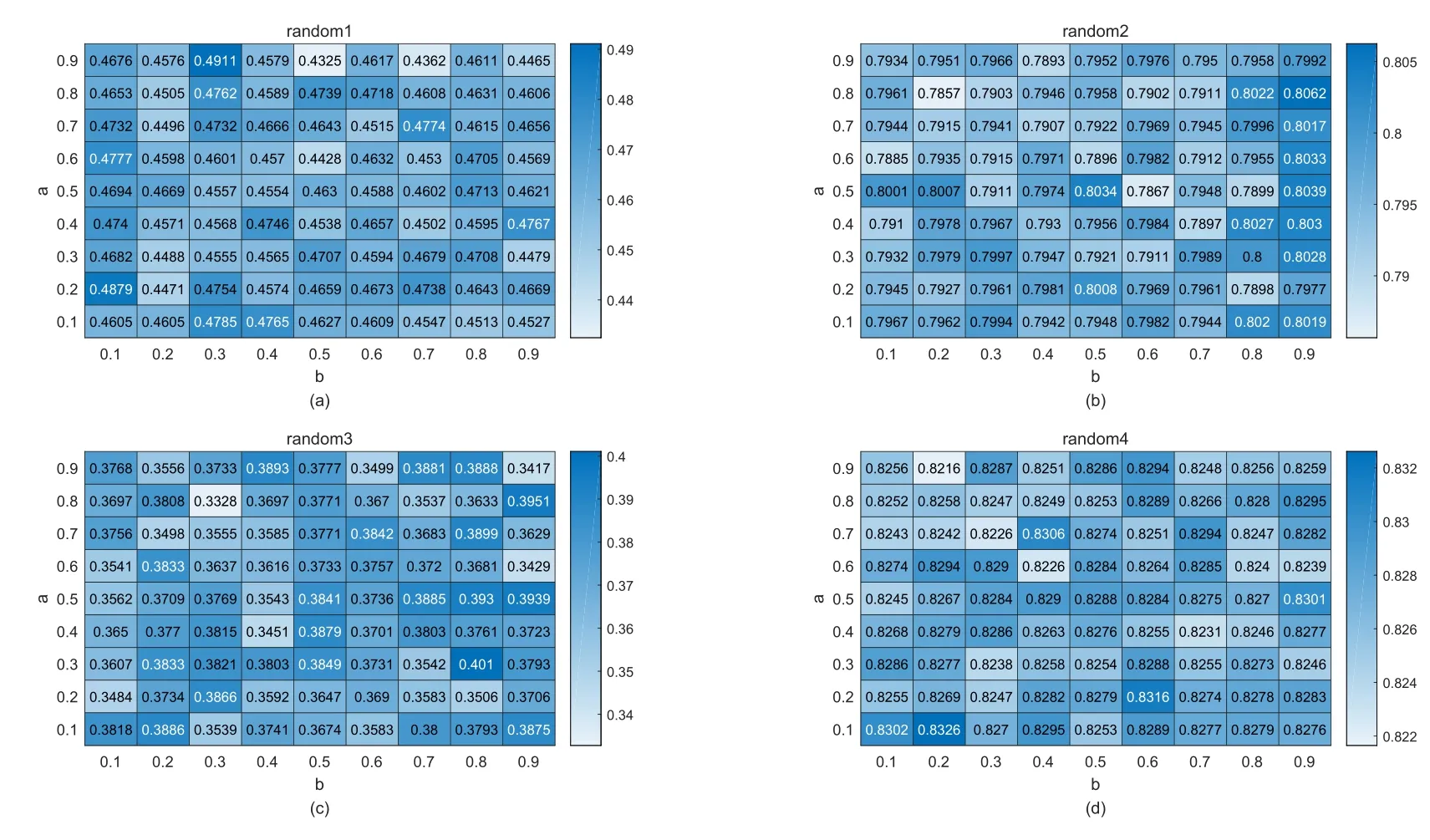
Figure2:Heat map on four random social network:we analyze the value of α and β in different random social network because α and β are unknow in Eq.(3).We study the correlation between the influence of node and the mixed importance of node by using kendall correaltion coefficient.The maximum τ in the heat map illustrate that the value of Eq.(3)with current α and β accord optimally with the real influence of node

In this section,we perform the mixed importance algorithm in the 4 random networks to find the optimal value ofαandβin the every dataset respectively.In Fig.2,the vertical axis represents the value ofα,the horizontal axis represents the value ofβ,and(α,β)corresponds to the value ofτ.In Fig.2(a),theτvalue of the random1 dataset is optimal,whenα=0.9andβ=0.3;In Fig.2(b),theτvalue of the random2 dataset is optimal,whenα=0.8andβ=0.9;In Fig.2(c),theτvalue of the random3 dataset is optimal,whenα=0.3andβ=0.8;In Fig.2(d),theτvalue of the random4 dataset is optimal,whenα=0.1andβ=0.2.

4.2 Comparison and analysis of the scope of influence

In the above experiment content,we achieve optimalαandβin the every dataset respectively.Then,we compare the influence of seed set selected by the mixed importance algorithm with the influence of seed set selected by other algorithms,such as Degree Centrality,PageRank[Page,Brin,Motwani et al.(1999)].We analyze the trend of the influence of the seed set selected by each algorithm,when we change the size of seed set.The experimental results show in Fig.3 and Fig.4.

Figure3:The scatter figure of influence of the seed set selected by mixed importance algorithm on 4 real dataset:every scatter figure has 10 point for every algorithm and we connect 10 points with a dotted line for observing the trend of influence

Figure4:The scatter figure of influence of the seed set selected by mixed importance algorithm on 4 random dataset:every scatter figure has 10 point for every algorithm and we connect 10 points with a dotted line for observing the trend of influence

4.2.1 Real network

In Fig.3 and Fig.4,the horizontal axis and the vertical axis respectively represents the size of seed set and the influence of the seed set.Fig.3(a)shows the influence range of the email.The influence of the mixed importance algorithm is almost the same as that of the degree centrality.The influence of the mixed importance algorithm is generally higher than that of PageRank.The seed set selected by the mixed importance algorithm has a good influence on the email.Fig.3(b)shows that the influence of the seed set selected by the mixed importance algorithm on the socfb Bowdoin47 is less than that of degree centrality,but the differences between the two algorithms are small.Fig.3(c)is the influence range of the hamsterster,and Fig.3(d)is the influence range of the socfbSmith60.Similarly,the influence of mixed importance is at least slightly less than the influence of degree centrality,but the scope of mixed importance is much larger than PageRank.

4.2.2 Random network

Fig.4(a)shows the influence range of the random1 dataset,and the influence of the mixed importance algorithm is almost the same as that of degree centrality.Fig.4(b)shows the influence range of the random2 dataset.The influence of the mixed importance algorithm exceeds that of degree centrality.In general,the influence range of the mixed importance algorithm is slightly smaller than that of degree centrality.Fig.4(c)shows the influence range of the random3 dataset.The influence ranges of the mixed importance algorithm and degree centrality are generally the same.Fig.4(d)shows the influence range of the random4 dataset,where the influence of the mixed importance algorithm and the influence of degree centrality are generally the same.

4.3 Comparison and analysis of impact cost

Finally,we compare the mixed importance algorithm with other algorithms,such as Degree Centrality,PageRank.We analyze the cost of the seed set selected by each algorithm,when we change the size of seed set.The experimental results show in Fig.5 and Fig.6.

4.3.1 Real network

In Fig.5 and Fig.6,the horizontal axis and the vertical axis respectively represents the size of seed set and the cost of the seed set.Fig.5(a)shows the cost of the email,where the cost of mixed importance algorithm,degree centrality and PageRank are similar.Fig.5(b)shows the cost of the socfbBowdoin47,Fig.5(c)shows the cost of the hamsterster,and Fig.5(d)shows the cost of the socfbSmith60.The cost of mixed importance algorithm and degree centrality are much higher than that of PageRank,and the cost of mixed importance algorithm is small compared to the Degree Centrality.

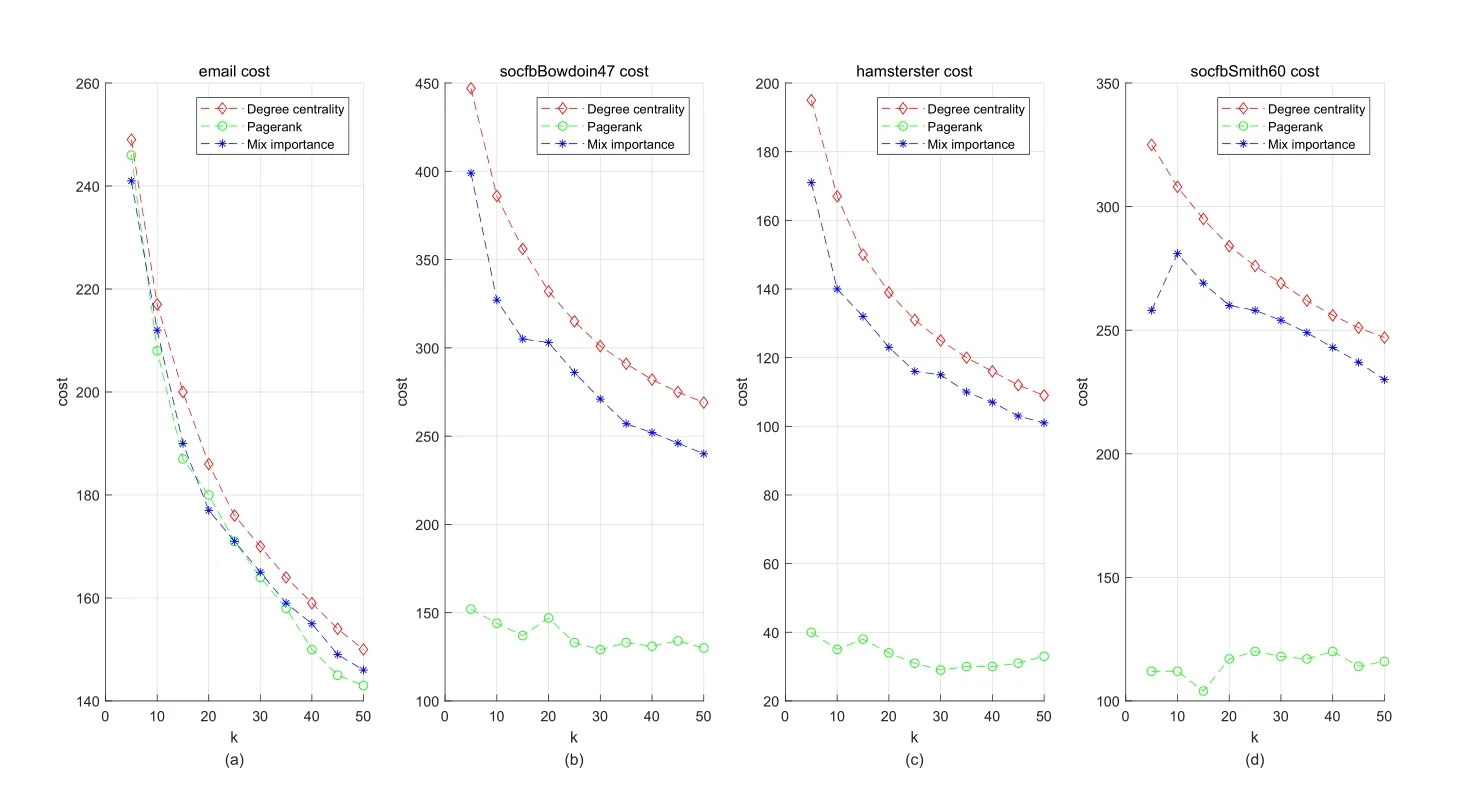
Figure5:The scatter figure of cost of the seed set selected by mixed importance algorithm on 4 real dataset:every scatter figure has 10 point for every algorithm and we connect 10 points with a dotted line for observing the trend of cost

Figure6:The scatter figure of cost of the seed set selected by mixed importance algorithm on 4 random dataset:every scatter figure has 10 point for every algorithm and we connect 10 points with a dotted line for observing the trend of cost

4.3.2 Random network

Fig.6(a)shows the cost of the random1,where the cost of mixed importance algorithm is slightly less than the cost of the Degree Centrality.Fig.6(b)shows the cost of the random2,and Fig.6(c)shows the cost of the random3.The cost of mixed importance algorithm is small compared to the cost of the Degree Centrality.Fig.6(d)shows the cost of the random4,where the cost of mixed importance algorithm and Degree Centrality are flat.In Fig.6,the cost of mixed importance algorithm is greater than the cost of PageRank.Based on the experimental comparison,the cost of PageRank is always less than the cost of mixed importance algorithm and Degree Centrality,but the range of in fluence of PageRank is also much smaller than that of mixed importance algorithm and Degree Centrality.The in fluence range of the mixed importance algorithm is equal to that of Degree Centrality,and the cost of mixed importance algorithm is much smaller than the cost of Degree Centrality.When the in fluence range of mixed importance algorithm is better than that of Degree Centrality,the cost of mixed importance algorithm is also less than the cost of Degree Centrality.The experiments show that the mixed importance algorithm has achieved good results.

5 Conclusion

This paper mainly analyzes how to effectively measure the influence of node in the process of influence maximization.The experiments show that the influence of a node is related not only to its degree,but also related to its coreness,as well as the degree and coreness of its neighbors.Therefore,we proposed an influence maximization algorithm based on the mixed importance of node.In this algorithm,the independent cascade model is used to simulate the influence of nodes.The Kendall correlation coefficient is used to measure the correlation of the mixed importance of node and the influence of node and the optimal values of two important parameters are achieved through calculation.The experimental comparisons of algorithms on four real datasets and four random datasets show that the influence maximization algorithm based on the mixed importance of node we propose in this paper achieved excellent performance.