《正弦定理》说课稿

李盼娟

(河南师范大学数学与信息科学学院，河南 新乡 453000)

各位评委老师好，今天我说课的题目是《正弦定理》。《正弦定理》是必修五第一章第一节的内容，我将以新课程标准的理念指导本节课的教学，从教材、教法、学法、教学过程和说课综述五个方面来谈谈我对教材的理解和教学的设计，请各位专家、评委老师批评指正。

一、说教材

(一)教材的地位和作用

本节课《正弦定理》选自《普通高中课程标准实验教科书数学·5》(必修)一书，是第一章“解三角形”的第一节内容，本节内容编排在学习了三角函数和三角恒等变换之后，这里我们多次用到正弦函数，进而通过本节课的学习既可以对正弦函数方面的知识加深理解，又可以为后面学习余弦定理打下基础，因此，《正弦定理》是本章的重要内容。它与我们日常、生活、生产和科学研究都有着紧密的联系，所以学习这部分内容有着广泛的现实意义。

(二)教学目标

1.知识与技能目标：学习正弦定理的定义，学会应用正弦定理来解三角形；

2.过程与方法目标：通过让学生观察，猜想，运用由特殊到一般的思想方法，注重正弦定理的推导证明过程，加深学生对定理的理解；

3.情感态度与价值观目标：在学习正弦定理的过程中，帮助学生养成勤于思考的习惯，在探究知识的过程中体会数学与生活的紧密联系[2]。

(三)教学重点和难点

1.重点：通过探索三角形的边角关系，发现并证明正弦定理，初步学会应用正弦定理解三角形；

2.难点：用“作高法”证明正弦定理，让学生掌握正弦定理的基本应用[3]。

二、说教法

(一)教学手段

基于新课程标准的要求和本节课知识内容的特点，为了使学生更好地理解并掌握正弦定理，在教学手段上采用板书、PPT和几何画板等多媒体相结合的方式，从问题情境创设入手，引导学生观察发现，从直观想象到发现猜想，再到抽象概括，最后得出结论，一步一步探索知识的生成过程，体会获得知识成果的喜悦。

(二)教学方法及其理论依据

本节课采用的教学方法是“发现探究法”，让同学们分组讨论，主动探究，合作交流，从现实中实际例子出发，利用此年龄阶段学生的好奇心和认知特点，一开始就抓住学生眼球，然后引导学生发现三角形的边角关系，师生进一步探究，以直角三角形为特例出发，将特殊到一般的数学思想渗透在教学过程中，从而得出正弦定理，并说明它在解三角形中的应用。教学中努力做到锻炼学生的思维，教会他们数学的思考方法，教师要真正做到“授之以渔”。

三、说学法

本节课的授课对象是高二年级的学生，经过之前一年的数学学习，学生已经学习过三角函数，有一定的知识储备，况且这一阶段学生对于前一段所学知识并没有完全遗忘，根据人的遗忘规律，及时复习，并引入新课，探索新知，明确学习目的，抓住学生数学学习的心理特点，运用生动形象，形式多样数学方法，深入浅出，让数学课堂真正成为探究性课堂，提高课堂效率。接下来我将说明以下几个方面的学法指导：

(一)培养学生通过观察、发现、探究、检验等方法，学习正弦定理的相关知识，从实例出发，寻求解决方法，发现三角形边角关系，进一步分析探究，归纳推理，推导出正弦定理，并加以证明，这正是一个分析和推理的全过程。

(二)学生独立思考，在探索性实验中以直角三角形为特例，并推广到一般情况，亲身经历定理证明的过程方法。如用“作高法”在直角三角形中进行证明完成后，分别又在“锐角三角形”和“钝角三角形”中，通过直观演示，计算推理，同样得到了正弦定理，这样，我们就可以把正弦定理推广到任意三角形的情形中去。

四、说教学过程

(一)创设情境，提出问题

如图1，河的两岸有A,B两点，要测量两点之间的距离.测量者在A的同侧，在所处的河岸边，选定一点C，测出AC的距离是55m，∠BAC=51°，∠ACB=75°.求A,B两点间的距离(精确到0.1m).

引导学生分清题意，在△ABC中，我们知道一条边AC的长度，并知道两个角∠BAC，∠ACB的大小，求其中一条边AB的长，启发学生用何种方法才能求解。

(二)提出问题，导入新知

我们知道，在任意三角形中有大边对大角，小边对小角的边角关系，那么对于上面情境中的三角形，我们能否得这个边、角关系准确量化的表示呢？如果大家对任意三角形知如何下手，那么能否优先考虑曾经学过边角关系的三角形，即直角三角形。

如图2，在Rt△ABC中，∠C是最大的角，所对的斜边c是最大的边，要考虑边长之间的数量关系，就涉及到了锐角三角函数.根据正弦函数的定义，

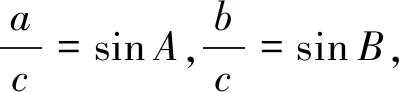
设计意图：从已学过的直角三角形出发，因为我们之前学过勾股定理，深入探讨边角关系，得到正弦定理，此时学生会有疑问，这样的等式是在直角三角形中推导出来的，那么在任意三角形(锐角三角形，钝角三角形)中仍然成立吗？接下来分小组讨论，我们继续深入探讨[1]。

(三)深入探究，得出结论

1.如图3，当△ABC是锐角三角形时，设边AB上的高是CD，根据三角函数的定义，

解：因为CD=asinB，CD=bsinA，所以asinB=sinA，

设计意图：由以上讨论，在锐角三角形中想

到“作高法”构造直角三角形，化未知为已知，进行学习迁移，进一步讨论。

2.如图4，当△ABC是钝角三角形时，过点C作AB边上的高，交AB延长线于点D，根据锐角三角函数的定义，

解：有CD=asin∠CBD=asin∠ABC，CD=bsinA.

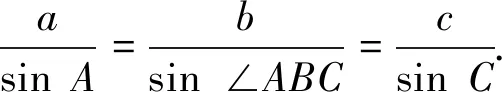
设计意图：同锐角三角形讨论方法类似，在这里我们仍然要引导学生构造直角三角形，利用同一条边长的不同表示，发现并得出正弦定理。

3.得出结论

正弦定理：在一个三角形中，每条边和它所对的角的正弦比是相等的，即

一般地，三角形中三个角A,B,C与它们的对边a,b,c叫做三角形的元素。如果已知三角形的几个元素来求其他元素的过程就叫做解三角形[1]。

(四)例题讲解，课堂练习

1.例题讲解

例1.在△ABC中，已知A=32.0°,B=81.8°,a=42.9cm,解三角形.

例2.在△ABC中，已知a=20cm,b=28cm,A=40°,解三角形(角度精确到1°，边长精确到1cm).

设计意图：在例1中已知两角及一边，解三角形即可求出另外两条边和一角；在例2中已知两边及一角，此时利用正弦定理解三角形时，要特别注意会出现解不确定的情况，一般可根据三角形中“大边对大角和三角形内角和定理”来取舍。

2.课堂练习

练习1.在△ABC中，已知A=60°,C=45°,c=20cm,解三角形(边长精确到1cm).

练习2.在△ABC中，已知a=20cm,b=11cm,B=30°,解三角形(角度精确到1°，边长精确到1cm).

设计意图：让学生在初步掌握了正弦定理的应用后，独立运用知识完成练习，巩固强化概念的生成和应用，将新知识进行内化。

3.解决引例问题

分析：要测量两点A、B之间的距离，所求的边AB的对角是已知的，又已知三角形的一边AC，根据三角形内角和定理可计算出边AC的对角，根据正弦定理，可以计算出边AB。

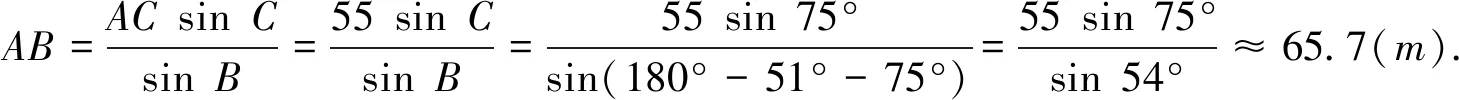
答：A,B两点间的距离为65.7米。

(五)归纳小结，知识升华

(六)作业布置

1.必做题：教材10页A组：第1题，第2题；

2.选做题：用“外接圆法”证明正弦定理，看看你有什么新的发现。

适当的作业布置可以使学生在课下巩固所学知识，作业有必做题与选做题，学生可以自主选择，主动探究学习，亲身经历知识获得的过程。

(七)板书设计

2.证明方法：作高法

3.解三角形：①已知两角和一边；②已知两边和其中一边的对角，板书的设计使学生对上课所学的知识一目了然，并能清楚地知道重难点，做到心中有数。

五、说课综述

以上是我对《正弦定理》这节课的认识和教学过程的设计，在整个课堂中，我引导学生回顾直角三角形中的勾股定理，作为探索三角形边角关系的出发点，并把所得结论推广到任意三角形中去，使学生进一步认识正弦定理，采用“特殊—归纳—猜想—证明”的数学思想方法并证明定理，逐步深化学生的认知活动，让学生既掌握了知识，又学会了方法。

总之，对课堂的设计，我始终按照新课标要求，坚持以学生为主体，以教师主导，并从各种实际出发，引导学生不断积极探索新知，锻炼学生思维，有计划地培养学生观察能力、应用知识能力和创造力。以上就是我对本节课的理解与设计，不足之处，请各位老师批评指正，我的说课到此结束，谢谢大家！