基于cmos反相器的可精确计算延时电路
2019-05-09崔建国宁永香
崔建国,宁永香
(山西工程技术学院,山西 阳泉 045000)
0 引言
在人们的日常生活或工农业电气设备控制方面,有众多场合都需要对电路进行延时开关,实现的方法有许多,可以用最简单的机械定时器实现定时或延时控制,也可以用较复杂的电脑通过编程实现。
当然,最常用的实现的方法是采用阻容RC定时网络电路连接一个反相器实现,见图1,这种电路非常方便、非常实用,常常在一些电子或电气控制电路中见到。遗憾的是,RC定时网络的每个元件数值均有明显的误差,以致不能事先精确地确定或计算延时的时间[1]。
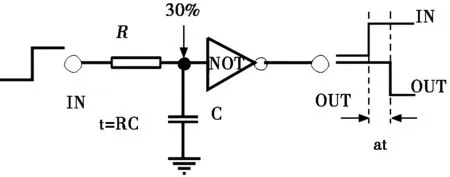
图1 一般延时器电气原理图
这里我们采用两个RC网络和两个反相器,依次串联,形成一个新颖的定时或延时电路,这样可以明显地改进延时的精确度。
1 一般延时器电路实际工作时获得的延时与设计初衷的差别
图1是一个比较典型、比较简单的延时器电路,采用阻容RC定时网络电路连接一个反相器实现,反相器是可以将输入信号的相位反转180°的电路,这种电路广泛应用在模拟电路中,比如音频放大,时钟振荡器等。
在电子线路设计中,经常要用到反相器。CMOS反相器电路由两个增强型MOS场效应管组成。而典型的TTL与非门电路由输入级、中间级、输出级组成。
以常用的CMOS反相器电路为例,图1所示的CMOS反相器的阈值电压为供电电压的一半,即1/2VCC,并有-15%~+15%合计30%的误差。其中τ是RC延时电路的时间常数,τ=RC;αt可以认为30%的阈值误差电压所造成的延时或定时的误差[2]。
图2示出了反相器电路的输入信号曲线,其中横轴为X,X=t/τ,X为时间常数τ的倍数,t为电容充电时间;纵轴为“1”,曲线代表函数1=e-X。
按照上文所指出CMOS反相器的阈值电压可能有30%的误差,那么在图1所示的延时电路中,如果输入电压UC(电容C上的充电电压)为0.35 VCC~0.65 VCC之间的任何一个电压值,图1中反相器的输出都有可能出现逻辑“0”或逻辑“1”的状态。
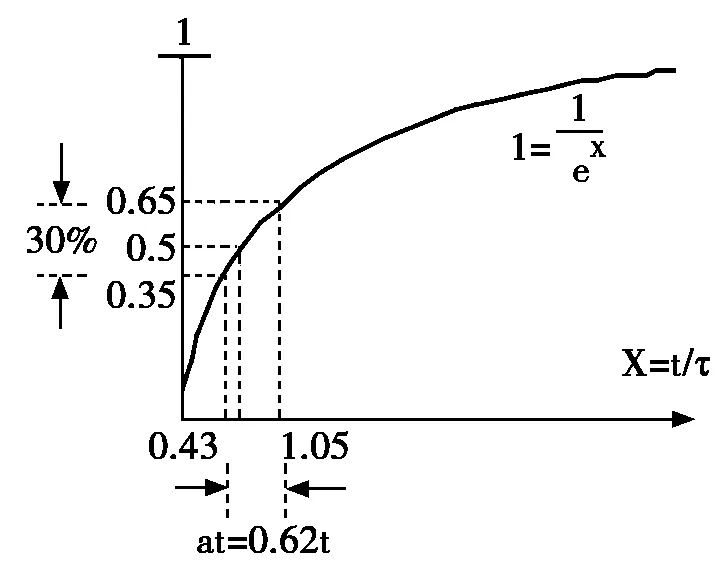
图2 CMOS反相器电路的输入信号曲线图
至于输出是“0”还是“1”,在于电容属于充电过程还是放电过程,充电过程中UC电压值超过反相器的阈值电压(可能0.35 VCC~0.65 VCC之间的任何一个电压值)时,反相器输出“0”;电容放电过程中,UC电压值低于反相器的阈值电压时,反相器输出高电平12 V(假如反相器供电为12 V)。
从图2可以看出,这两种状态(0.35 VCC以及0.65 VCC)分别对应于电容通过电阻充电到0.43τ和1.05τ(τ=RC)的时间。因为CMOS反相器的阈值电压为供电电压的一半,故阈值电压UC=0.5 VCC时,图2中对应的电容充电时间要在t=0.69τ后才出现。
对上面的关键点总结一下,我们通常设计延时电路时,一般以UC=0.5 VCC作为阈值电压来计算延时时间,即电容的充电时间t=0.69τ时,反相器输出电平开始反转,但由于CMOS反相器的阈值电压可能有30%的误差这种特性,最后实际运行所得到的延时时间有可能是UC(反相器输入电压)为0.35 VCC~0.65 VCC中的任意一点作为阈值电压时的时间[3]。
所以在图1延时电路中,以UC=0.5 VCC作为阈值电压设计延时所获得的时间与设计初衷之间的误差还是很大的,工程师设计的参数不能直接拿来引用。
2 可精确计算的延时电路的分析
设计一个延时电路,这个延时电路仍以UC=0.5 VCC作为阈值电压设计延时,对应的电容充电时间t0.5VCC=0.69τ。经过反复验证,延时电路实际运行所得到的延时时间与设计初衷所计算的延时时间虽然不是完全一样,但它们之间的误差已经大大缩小,设计参数可以直接引用。
这个延时电路采用了两个RC网络和两个反相器,如图3所示,图中的每个RC网络产生相同的延时,且都等于图1所示电路总延时值的一半,第一个RC延时电路的延时值t1=0.5*X1*τ,对照图2,其中X1*τ为第一个反相器的有误差阈值电压对应的充电时间;第二个RC延时电路的延时值t2=0.5*X2*τ,仍对照图2,其中X2*τ为第二个反相器的有误差阈值电压对应的充电时间。
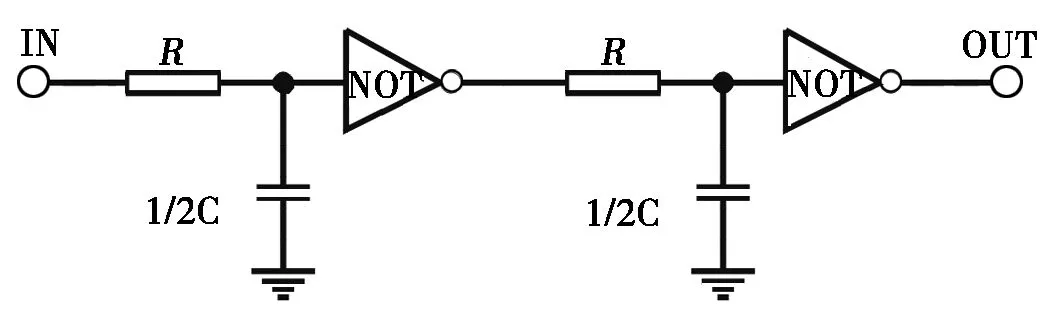
图3 可精确计算的延时电路1电气原理图
故图3延时电路的总延时t可以用以下公式简单计算:
t=t1+t2=(0.5*X1*τ)+(0.5*X2*τ).
其中τ为RC延时电路的时间常数,τ=RC;X1与X2皆为0.43~1.05之间的任意一个值,X1或X2与τ的乘积就是各个反相器有误差的阈值电压所对应的充电时间。
以上求总延时公式我们可以以任意组合来计算其实际延时时间,从而与以UC=0.5 VCC作为阈值电压时的设计延时时间作比较,来验证我们设计的合理性。
首先以第一种情况 验证图3设计的合理性,即第一个延时网络中的反相器以-15%的阈值电压误差求其实际延时时间t1=0.5*X1*τ=0.5*0.43*τ;第二个延时网络中的反相器以+15%的阈值电压误差求其实际延时时间t2=0.5*X2*τ=0.5*1.05*τ,故实际总延时为
t=(0.5*0.43*τ)+(0.5*1.05*τ)=0.74τ.
由此可以看出,虽然设计延时时间0.69τ与实际延时时间0.74τ之间仍有差距,但已经很接近设计值0.69τ。
第二种情况,如果第一个延时网络中反相器恰好阈值电压为0.5VCC,第二个延时网络中反相器阈值电压也恰好为0.5VCC,那么实际总延时为
t=(0.5*0.69*τ)+(0.5*0.69*τ)=0.69τ.
这种情况下的设计延时与实际延时恰好一样。
第三种情况,如果第一个延时网络中反相器阈值电压为0.65VCC,第二个延时网络中反相器阈值电压也恰好为0.65VCC,那么实际总延时为
t=(0.5*1.05*τ)+(0.5*1.05*τ)=1.05τ.
这是两个反相器阈值电压误差最大、情况最恶劣的一种组合,其设计延时0.69τ与实际总延时1.05τ相差还是蛮大的。
但第三种情况是一种特例,通过大量任意阈值电压组合的比较,我们可以证明采用图3设计方案所得到的延时器,相比较图1的一般延时器,工程师设计的延时时间与延时电路实际运行所得到的延时时间虽然不能完全一模一样,但它们之间的误差已经大大缩小,可以认为图3的延时电路是可以被精确计算的,设计参数是可以拿来直接引用的。
从以上的分析我们就可以明白图4所示的电路也可得到同样精确的总延时。图4的工作原理仍然利用两个反相器的阈值电压的误差不总是处于最恶劣的状况,仍然可以以两个反相器阈值电压的误差的任意组合来计算其实际延时时间,从而证明图4所示的电路也可得到同样精确的总延时,这里不再重复证明。

图4 可精确计算的延时电路2电气原理图
3 注意事项
图3的延时电路要想获得满意的结果,还有一个注意事项,就是其中的反相器必须采用CMOS反相器,其主要原因在于只有CMOS门电路的阈值电压为供电电压的一半,而且他们的输出电压只能是“0”或“供电电压值”,这里是不能采用斯密特触发器的,因为斯密特触发器有两个阈值电压,且不一样[4]。
若采用4000系列的CMOS电路,其延时时间太长的话,可采用74HCXX系列电路,74HCXX系列电路的引脚功能和L4LSXX系列兼容。
4 结语
本设计的延时电路采用两个RC网络和两个反相器串联,每个RC延时器得到的实际延时虽然与设计值仍有误差,但由于两个延时器其误差方向不可能总是相同,故它们的总延时与设计值相差并不大,有时甚至相同。这个电路设计虽然不能彻底解决误差的存在,但可以将误差尽可能缩小。
本设计的不足是反相器必须采用CMOS门电路,斯密特触发器、TTL门电路不适合这种设计。
