一种用于BDD模型构建的排序起点选择新方法*
2019-05-09潘竹生曾令国
潘竹生, 王 晖, 曾令国
(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
0 引 言
二元决策图即BDD(binary decision diagram)及其扩展形式已广泛应用于众多领域,如电路验证[1]、紧凑马尔可夫链表达式[2]、编程中对大型元组集的有效处理[3]、符号模型检验[4]和各种类型系统[5]的可靠性分析等,有着出色的应用表现.
所有基于BDD的方法,其性能都非常依赖变量排序.不同质量的变量排序指导生成不同规模的BDD模型,BDD规模大小通常跨越几个数量级[6].更不幸的是,寻找最优排序是一个NP完全问题[6].因此,在实际应用中多采用启发式变量排序[7-8]策略,其中在网络可靠性分析领域,一般采用广度优先搜索BFS(broad first search)和深度优先搜索DFS(deep first search)这2种排序[9].文献[10]比较了BFS和DFS两种策略在规则网络可靠性分析中的性能,得出BFS策略优于DFS;文献[11]深入研究了BFS排序策略,指出源点一般不是最佳排序起点,对于Square Lattice网络,最佳排序起点分布在4个角上;文献[12]结合网络结构特征提出了一种启发式策略的选择方法,用于构建精简BDD模型.总结现有研究成果,针对启发式排序,主要研究排序策略本身,并且认为“源点,即可靠性网络中的一个关键节点,就是最佳排序起点”[7].
事实上,排序起点和排序策略一样,同样严重影响排序结果.本文尝试为节点建立指标数据,研究基于指标数据的最佳排序起点选择方法.
1 网络模型和常用启发式排序
1.1 网络模型
研究网络可靠性时,通常将网络建模成一个无向图G=(V,E,K).其中:V是节点集,表示网络系统中的实体;E是边集,表示实体之间的连接;K⊆V是网络中的关键节点(|K|≥2,k=|K|表示集合K的长度),表示网络中特别重要的实体.所谓网络可靠性,是指K中节点完全连通的可能性.根据集合K大小的不同,将可靠性问题分为3类:2-端网络可靠性(|K|=2)、k-端网络可靠性(2<|K|<|V|,|V|表示集合V的长度)和All-端网络可靠性(|K|=|V|).本文研究2-端网络可靠性,图1所示为3×3 Square Lattice网络G(V,E,K)=({n0,n1,n2,n3,n4,n5,n6,n7,n8},{e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12},{n0,n8}),|K|=2.
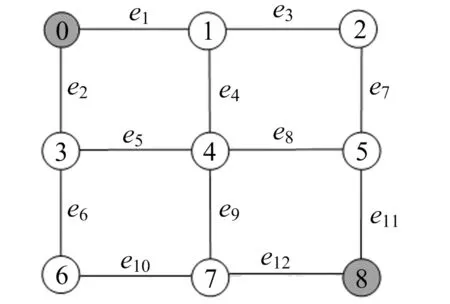
图1 3×3 Square Lattice网络
1.2 常用启发式排序
最优排序能生成最简BDD模型,然而求解最优排序是一个NP完全问题[6].因此,在工程应用中多采用启发式排序,常见的有BFS和DFS.
1.2.1 BFS启发式排序
BFS即广度优先搜索,是图的一种遍历方法.遍历从某一点v开始,沿着关联于v的边ei(1≤i≤|E|),分别访问节点ni(1≤i≤|E|且ni≠v).根据广度优先策略,再分别由节点ni(1≤i≤|V|且ni≠v)出发,沿着相关边遍历其他节点,直到所有边和节点被访问.按遍历过程中出现的顺序排列边,即得到BFS启发式边排序;排列节点,则得到节点序;若考虑二者,则得到节点和边的混合排序.如图1所示网络,假设排序起点v=n0,若按小编号优先进行广度遍历,则得到边序为e1≤e2≤e3≤e4≤e5≤e6≤e7≤e8≤e9≤e10≤e11≤e12,节点序为n0≤n1≤n3≤n2≤n4≤n6≤n5≤n7≤n8,混合排序为n0≤e1≤e2≤n1≤e3≤e4≤n3≤e5≤e6≤n2≤e7≤n4≤e8≤e9≤n6≤e10≤n5≤e11≤n7≤e12≤n8;改变排序起点v=n4,则边序为e4≤e5≤e8≤e9≤e1≤e3≤e2≤e6≤e7≤e11≤e10≤e12,节点序为n4≤n1≤n3≤n5≤n7≤n0≤n2≤n6≤n8.
1.2.2 DFS启发式排序
DFS即深度优先搜索,是另一种图遍历方法.遍历从某一点v开始,沿着关联于v的边ei(1≤i≤|E|),访问节点ni(1≤i≤|V|且ni≠v),再从节点ni出发,进行深度优先遍历,直到所有的边和节点被访问.按遍历过程中出现的顺序排列边,得到DFS边排序;排列节点,得到节点序;排列边和节点,得到边和节点的混合排序.如图1所示网络,假设排序起点选择n0,若按小编号优先进行深度遍历,则得到边序为e1≤e3≤e7≤e8≤e4≤e5≤e2≤e6≤e10≤e9≤e12≤e11,节点序为n0≤n1≤n2≤n5≤n4≤n3≤n6≤n7≤n8,混合排序为n0≤e1≤n1≤e3≤n2≤e7≤n5≤e8≤n4≤e4≤e5≤n3≤e2≤e6≤n6≤e10≤n7≤e9≤e12≤n8≤e12;若排序起点选择n4,则边序为e4≤e1≤e2≤e5≤e6≤e10≤e9≤e12≤e11≤e7≤e3≤e8,节点序为n4≤n1≤n0≤n3≤n6≤n7≤n8≤n5≤n2.
显然,不同的排序起点,有完全不同的排序结果,进而导致规模大小迥异的BDD模型.
2 排序起点选择方法和证明
2.1 依赖集和依赖集总长度
定义1(依赖集dependency set) 对于k-端网络G= (V,E,K),设有一个部件序列o=c1≤c2≤…≤c|V|+|E|,ci∈V∪E,i∈[1,|V|+|E|],v∈V,则第i层依赖集Di定义为:Di={v|v已经排序且至少存在一条关联于v的未排序边}∪{v|v未排序且至少存在一条关联于v的已排序边}.集合Di中节点的数目定义为第i层依赖集长度,记为Li.如图1所示的3×3网络中,设有排序o=n0≤e1≤e2≤n1≤e3≤e4≤n3≤e5≤e6≤n2≤e7≤n4≤e8≤e9≤n6≤e10≤n5≤e11≤n7≤e12≤n8,则各层依赖集及依赖集长度如表1所示.

表1 排序o的各层依赖集及依赖集长度(3×3 Square Lattice网络)
定义2(依赖集总长度) 对于k-端网络G=(V,E,K),设有一个部件序列o=c1≤c2≤…≤c|V|+|E|,ci∈V∪E,i∈[1,|V|+|E|],则序列o的依赖集总长度(total length of dependency set,记为TLDS(o))定义为
其中,Li为序列o的第i层依赖集长度.如图1所示网络,序列o(o=n0≤e1≤e2≤n1≤e3≤e4≤n3≤e5≤e6≤n2≤e7≤n4≤e8≤e9≤n6≤e10≤n5≤e11≤n7≤e12≤n8)的依赖集总长度为28.
2.2 排序起点选择方法
对于网络G=(V,E,K),在确定排序策略(如BFS或DFS)的前提下,计算不同排序起点的依赖集总长度TLDS(order(v)),其中order(v)是以v(v∈V-K)为排序起点的一种排序结果,选取TLDS值最小的节点v作为排序起点,即
Chosen(V)=v⟺TLDS(v)=min{TLDS(v),v∈V-K}.
2.3 关于排序起点选择的思考和讨论
为何要选择TLDS值小的节点作为排序起点呢?这需要先来研究基于依赖集分区的子网特征标识技术[9]和BDD模型构建过程[9].
定义3(依赖集分区) 对依赖集中的节点按如下规则建立划分,按某种顺序排列所有划分,得到一个分区,称该分区为依赖集分区.
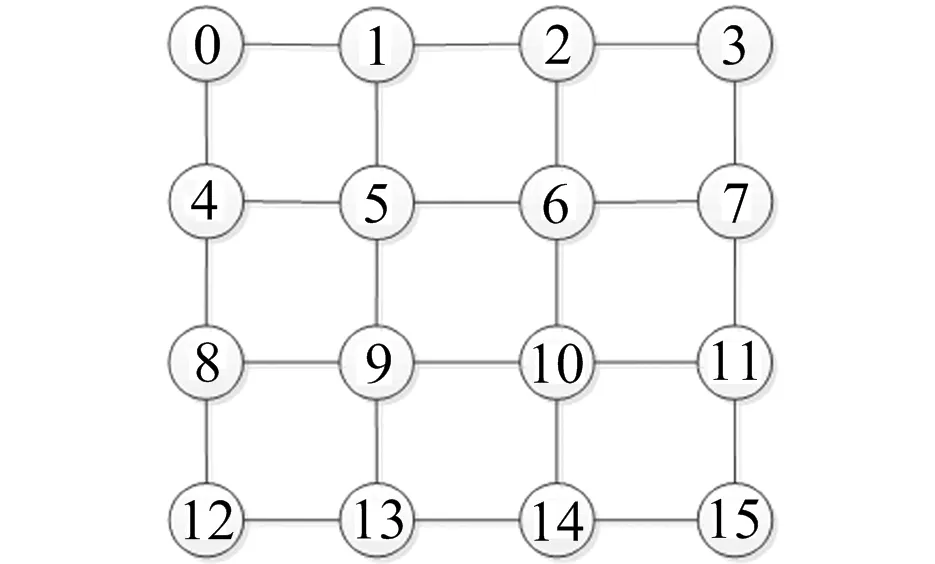
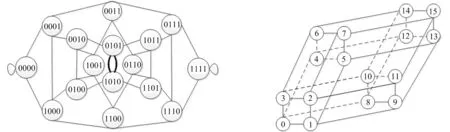
1)对于第i层依赖集Di中的任意2个节点u 2)若节点v∈Di失效,则首先将节点v从划分中分离出来,并给节点v加“#”; 3)若节点v∈Di和K′中的某一节点之间存在一条成功路径,则给节点v加“*f(v,K′)”,其中K′是集合K的一个有序序列,函数f是节点v与K′中节点的连接关系,即 f:(v,K′)→Z. 其中,Z是自然数集,用Z中元素的二进制位来表示节点v与K′中节点的连接关系.若连通,则将该位置为“1”,否则将其置为“0”.二进制位从右向左依次对应K′中的第1个节点至第|K′|个节点. 图2 桥接网络 图3是图2桥接网络在排序n0 图3 依赖集、依赖集分区和BDD生成过程 一条成功路径,即f(n3,{n0,n3})=(11)2=1+2=3.显然,构建任意一层BDD节点时,每个依赖集分区对应一个子网,而每个子网都可以由依赖集分区唯一标识. 进一步研究发现,依赖集分区建立在“n个有区别的节点,分配到m(0 其中,S(n,m)为第二类斯特林数,表示对n个数作m个划分.当第i层依赖集元素个数n较大时,Bn较大,即分区总数较多.所以,控制n的大小有助于控制分区数目,即BDD节点数.若能将每层依赖集都控制到最小,就有望构建规模最小的BDD模型. 考虑给节点加“*”时,依赖集中的每个节点都有可能加“*”,所以有n个节点的依赖集,其分区数目为2nBn.分区数目与n有关,n小,则分区数目就小.所以,如果每层取得最小(或较小)依赖集,那么在大概率上可以得到最小(或较小)BDD模型. 综合以上两方面分析可得,控制依赖集大小,能有效控制当前层的BDD节点数目.控制每层依赖集的大小,就可以控制整个BDD的规模.依赖集总长度TLDS由各层依赖集长度累加得到,当取最小TLDS值时,各层依赖集长度最小(或较小),所以,理论上有助于获得规模最小(或较小)的BDD模型.值得注意的是,加“*”操作严重影响分区空间,对于有n个元素的依赖集,加“*”操作,将分区空间扩展为原来空间的2n倍,这非常不利于精简BDD模型的生成.所以,一般而言,关键节点不宜用作排序起点[11]. 接下来用实验来验证所提方法的有效性.选择常用的BFS和DFS启发式排序策略,分别在Square Lattice、De-Bruijn和Hyper Cube网络中实验.实验过程:首先建立以每个节点为排序起点的BFS和DFS策略下的排序,得到排序结果并计算这些排序结果的TLDS值;其次,为每个2-端可靠性问题采用不同排序结果指导生成BDD模型,并统计BDD规模的大小情况;最后,统计当TLDS值最小(较小)和最大(较大)时对应的BDD规模大小的分布. Square Lattice 网络在分布式并行计算、分布式控制、CMOS电路、容量限制、路由优化、无线传感网络等领域有着广泛的应用[13].图4是一个4×4 Square Lattice网络.对于BFS和DFS排序策略,计算不同排序起点的依赖集总长度TLDS值,结果如表2所示. 图4 4×4 Square Lattice网络 节点TLDSBFSDFS节点TLDSBFSDFS0123150814515411341419194179213914710206184312315011145155413914212123175517018113154158617815414165181713914115123188 在相同排序策略下,1个排序起点对应1个排序结果,得到1个BDD模型.对于4×4 Square Lattice网络,共有120个2-端可靠性问题,任一可靠性问题有16个不同的BDD模型,记录16个不同排序起点所对应的BDD模型的大小情况.统计所有120个2-端可靠性问题在最小(较小)TLDS值时取得最小(较小)BDD模型的次数,和在最大(较大)TLDS值时取得最大(较大)BDD模型的次数,得表3和表4.表3和表4中1—16表示同一可靠性问题的不同BDD模型的大小次序,“1”代表最小BDD模型,“16”代表最大BDD模型,这些符号也适用后续表格. 由表3可得,对于BFS策略,当选择具有最小TLDS值的节点作为排序起点时,生成的BDD模型规模普遍较小,其中最小至少占21.7%(如节点“0”和“3”),节点“12”高达24.2%;前三小至少占49.2%(如节点“3”),节点“0”高达57.5%;当选择具有最大TLDS值的节点(如“10”)作为排序起点时,在120个样本中,有86个BDD模型的规模最大,29个第二,5个第三,前三大占100%. 表3 节点具有最小(大)TLDS值时 最小(大)BDD模型出现的次数(BFS) 注:节点“10”的TLDS值最大,节点“9”次之,节点“6”第3大. 表4 节点具有最小(大)TLDS值时 最小(大)BDD模型出现的次数(DFS) 注:节点“15”具有最大TLDS值,节点“10”次之,节点“5”和“14”第3大. 分析表4可得,对于DFS,当选择具有最小TLDS值的节点作为排序起点时,生成的BDD模型中,有61.7%(节点“1”)或34.2%(节点“7”)为前三小;相反,当选择具有最大或较大TLDS的节点作为排序起点时,生成的BDD模型普遍较大. 选择广泛应用于分布式计算、容错计算、并行路由等领域的De-Bruijn网络[14](见图5)和Hyper Cube[15]网络(见图6)继续实验,得到的实验数据如表5~表10所示. 对于BFS排序策略,随机选择4种BDD模式,结果如表9所示.显然,在TLDS值相同时,不同BDD模式在各个节点的分布相对均衡,间接说明TLDS值和BDD规模的相关性. 表6、表7和表10都说明:TLDS值与BDD规模之间存在相关性.TLDS值小,对应的BDD模型较小;TLDS值大,对应的BDD模型较大.在选择排序起点时,应尽可能选择TLDS值小的节点. 图5 4阶De-Bruijn网络 图6 4-Dimensional Hyper Cube网络 节点viTLDSBFSDFS节点viTLDSBFSDFS节点viTLDSBFSDFS节点viTLDSBFSDFS0196249419524781992471227526112042465233243924224213230268219922162622461022924614229268326625272482331123223715213272 表6 节点具有最小(大)TLDS值时,最小(大)BDD模型出现的次数(De-Bruijn BFS) 注:节点“4”的TLDS值最小,“0”次之;节点“12”的TLDS值最大,节点“3”次之. 表7 节点具有最小(大)TLDS值时,最小(大)BDD模型出现的次数(De-Bruijn DFS) 注:节点“2”的TLDS值最小,“7”次之;节点“15”的TLDS值最大,“13”“14”次之. 表8 各节点依赖集总长度TLDS(Hyper Cube 4-D) 表9 当TLDS值相同时,不同规模BDD模型出现的次数(Hyper Cube 4-D BFS) 表10 节点具有最小(大)TLDS值时,最小(大)BDD模型出现的次数(Hyper Cube 4-D DFS) 注:节点“4”和“5”具有最小TLDS值,节点“0”“1”“2”“3”次之;节点“14”和“15”具有最大TLDS值,节点“10”“11”次之. BDD模型的大小依赖于排序质量的高低,排序质量受排序策略和排序起点的影响.在排序策略确定的情况下,排序起点是影响排序质量的最重要因素.本文就排序起点的选择展开研究,提出“TLDS值小优先”的排序起点选择方法.理论和实验都表明:TLDS值和BDD规模之间存在相关性,即“小值TLDS节点通常生成较小规模的BDD模型,大值TLDS大概率产生较大规模的BDD模型”.在选择排序起点时,TLDS值小的节点具有优势,应该优先考虑.除了排序起点影响排序质量外,还有排序策略本身.今后将继续研究排序策略选择方法及排序起点选择、排序策略选择与网络结构特征的相关性.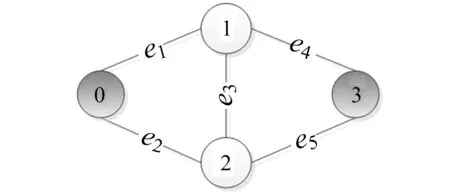

3 实验和结论
3.1 Square Lattice网络



3.2 其他网络






4 结 语
