基于混沌粒子群优化算法的相机参数标定方法
2019-05-09王琳霞陈广锋
王琳霞,陈广锋
(东华大学 机械工程学院,上海201620)
近年来随着科学技术的发展,计算机视觉技术领域的研究越来越深入,图像由二维转向三维重建是未来图像的发展趋势,三维重建目前一般使用双目立体视觉系统。 双目立体视觉可以看作是一个仿生的成像模式,主要模仿的是人类视觉系统。 它实现了人类可以从图片中直观认识三维事物,即从2D图像中分析并重建出3D 信息的方法。 而双目摄像机的标定是后续视觉处理的基础以及二维投影图像坐标与三维物体的世界坐标转换的关键步骤[1]。
相机标定的方法有传统标定方法(强标定)、自标定方法(弱标定)以及主动视觉标定方法[2-3]。 传统标定方法精度高,可以标定任何相机模型,但是计算过程复杂,需要标定块。 自标定方法不需要标定块,但是标定精度没有传统标定方法精度高。 主动视觉标定方法[4-6]通常可以线性求解,鲁棒性较强,但是不能应用于相机运动无法控制的情况。 但是在标定精度要求较高的场合中一般都使用传统标定方法,目前常用的标定方法有Abdel-Aziz[7]提出的线性标定法、Tsai 两步法[8]、张正友标定法[9]等。 张正友标定法脱离了传统的在高精度标定台上进行标定图像采样的做法,可以通过拍摄各个方位的标定板来实现对摄像头内外参数的求解。 但是在张正友标定算法中的非线性优化算法很容易陷入局部最优解,降低了标定精度。
本文在研究相机成像模型的基础上,对相机的内外参数进行求解。 先利用张正友标定法对单目摄像头进行标定,分析了张正友标定法在求解过程中存在的不足,进而提出了基于混沌粒子群算法对相机参数进行优化, 利用该算法提高了标定的精度。最后得出双目相机的内外参数,并且基本消除了相机的径向畸变。
1 相机成像模型
视觉系统获取图像是一个比较复杂的过程,在描述获取图像与摄像头之间的关系时,一般在视觉系统中主要使用4 种坐标系[10],各个坐标系均满足右手法则,下面以图1 为例来说明这4 种坐标系之间的关系。 图1 中的Ow-XwYwZw表示世界坐标系,用来表示实际中物体位置点的绝对坐标;Oc-XcYcZc表示相机坐标系, 其中Oc表示相机的光心,Zc轴和相机的光轴重合;O0-uv 表示图像像素坐标系,其中O0表示图像平面的原点, 位于CCD 图像平面的左上角, 坐标轴u 轴和v 轴分别表示向右和向下。 投影坐标使用(u,v)来表示,表示图像像素具体位置,即行列数。O1-xy 表示图像物理坐标系,O1是光轴与成像平面的交点。 图像物理坐标系是连续的,具有实际的长度单位,解决了像素坐标系只能离散地表示像素位置的问题,便于后续坐标系之间转换。
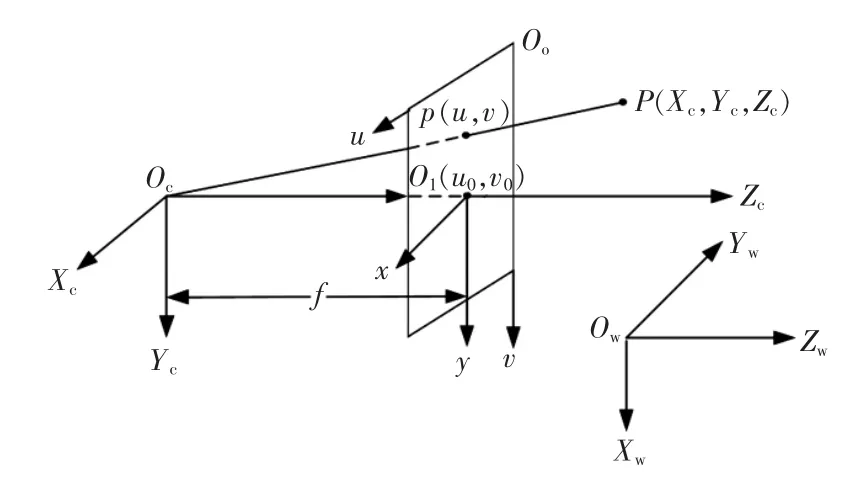
图1 相机成像模型Fig.1 Camera imaging model
理想的相机成像模型是针孔成像模型, 依据该模型图1 中各个坐标系之间的转换关系如式(1)所示:
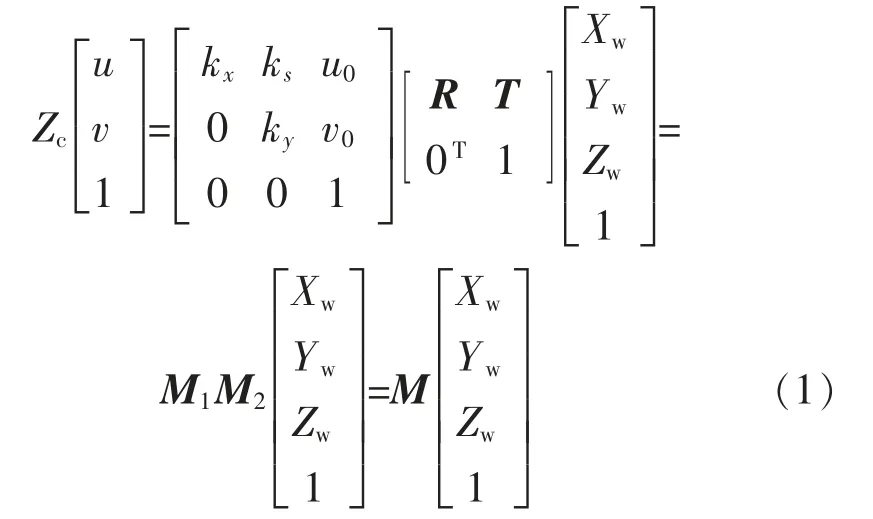
式中:kx=f/dx,ky=f/dy表示图像像素坐标系中u 轴和v 轴的尺度因子;M 是3×4 的矩阵, 称为投影矩阵[3];矩阵M1代表了摄像机的内参数,包括kx、ky、ks、u0、v0,完全由相机本身决定;矩阵M2代表了摄像机外参数,分别由旋转矩阵和平移向量所决定。 由此,通过式(1)表示了图像像素坐标与世界坐标系之间的一一对应关系。
实际应用过程中因制造、安装等因素,相机势必会有各种畸变[3]。 为了描述畸变成像的规律,就引入了非线性的成像模型。 所以实际的镜头成像都存在偏差,在实际求解内外参数的过程中需要考虑这些偏差部分,设实际图像点的坐标为(ud,vd),理想的坐标为(uu,vu),则考虑畸变的影响后,对应的关系如式(2)所示:
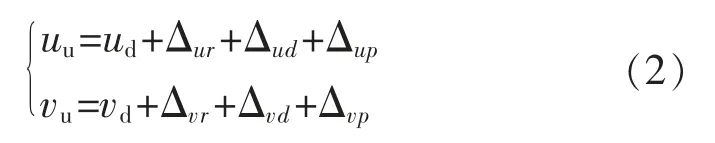
通常只考虑径向畸变也能实现较高的精度,满足应用要求。
因此式(2)可以转换为式(3)的形式:
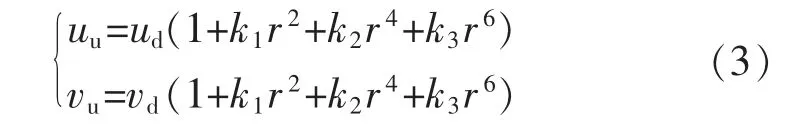
式中:k1、k2、k3为畸变参数,表示在水平和垂直方向的2 阶、4 阶和6 阶的畸变参数。
2 确定相机内参初始值
在张正友标定法中首先把标定板选作为世界坐标系的平面, 所以在标定板上的特征点(xwi,ywi,zwi)中的zwi的值为零,同时也设定该点对应的相机坐标值为(xci,yci,zci),图像像素坐标值为(ui,vi),对应关系为式(4):

因为单位向量n 与o 是正交的,通过式H=M[n o p]=[h1h2 h3]于是得到下面的约束:
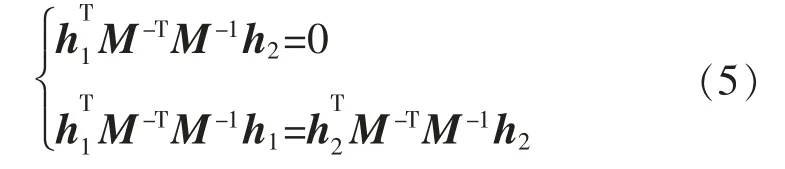
通过式(5)可以求解出M 值,可以求解相机参数。 观察式(5)可得,约束式的两个等式均含有一个相同的因式M-TM-1,而且M 为3×3 矩阵,所以为了简化计算,在这里令一个3×3 的矩阵B=M-TM-1,如式(6):
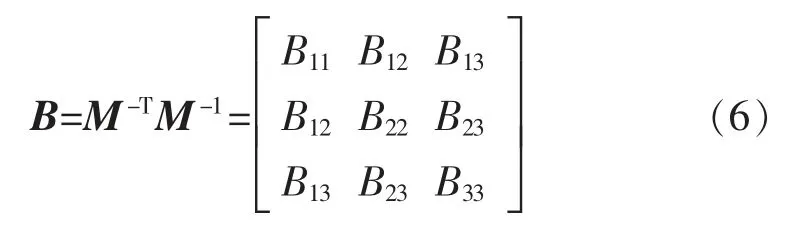
式中:B 是一个对称矩阵,将这6 个未知数定义为一个向量b:
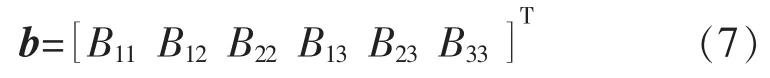
所以将矩阵B 和向量b 的关系可以写为

若有n 副平面模板图, 就能够获得n 个式(8)所示等式,将其写成为

式中:V 是2n×6 的矩阵。
若采集的图像n≥3 时,V 的最小特征值对应的特征向量即为b, 根据上述推导过程就可以计算出相机的5 个内参如式(10)所示:
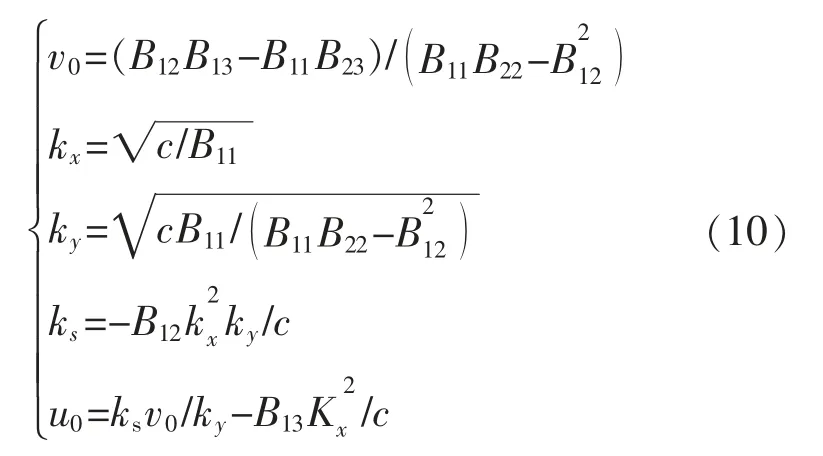
3 基于混沌粒子群优化算法对相机参数的优化
在上述张正友相机标定中,是通过假设摄像机为线性模型得到相机的初值, 并通过LM 法对初值进行优化,求解出单应性矩阵的初始值。 但是张正友标定法是基于相机的线性模型估计畸变参数,而且像LM 这种传统的优化策略容易陷入局部最优的情况,在标定精度上会有所降低。 为了提高相机的标定参数精度, 本文提出将混沌粒子群优化算法(CPSO)用在相机的标定对内外参数的优化过程中,以便使得相机参数解可以大概率的收敛于全局最优解,得到精度更高的标定参数。
粒子群优化算法(PSO)[11]是通过研究鸟群捕食行为演化得出的。 该算法的主要逻辑是在系统初始化一组随机解的基础上迭代寻优。 该算法在组合优化、非线性连续优化等方面应用十分广泛。
该算法的思想是:首先使得PSO 初始化为一群随机粒子,在之后的每一次迭代,粒子跟随两“极值”来更新自身。 这里涉及到两个极值点:个体极值点和全局极值点。 前者是通过自身寻找的最优解,位置使用pbest表示; 后者是是基于整个种群寻找的最优解,位置用gbest表示。 在PSO 中粒子通过位置收敛、更新速度来获取最优的解,根据式(11)和式(12)所示:
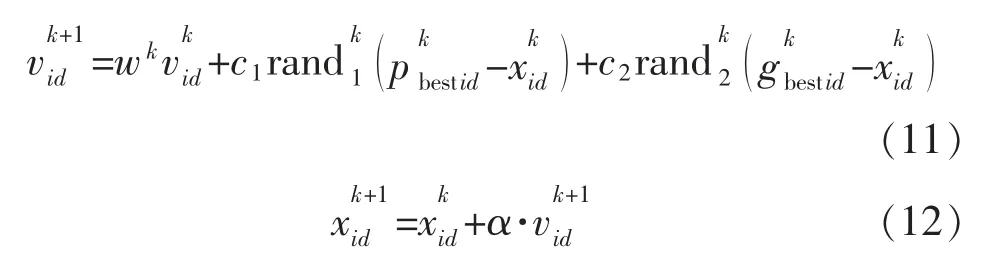
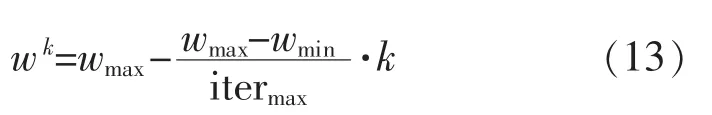
式中:itermax为最大进化代数;wmin和wmax为wk取值的范围。
可以得到,PSO 不论在初始化还是在进化过程中都具有随机性,对个体质量不能保证,容易影响进化过程的收敛,以及进化过程容易过早地收敛到局部最优点,导致精度不高。 所以针对这些不足,为了更好地提高在空间中的搜索能力,并且根据混沌变量具有的遍历性等优点,在本课题中利用基于混沌优化思想的混沌粒子群优化算法来对相机的参数进行优化。
CPSO 是把混沌变量从混沌空间映射到解空间,再利用混沌变量具有遍历性、随机性等特点来搜索。 混沌优化算法具有不对初值敏感、易跳出局部极小、搜索速度快、计算精度高、全局渐近收敛的特点[11]。
Logistics 方程是一个典型的混沌系统, 该方程与相比其他混沌系统来说计算量较小,所以本文采用此方程来构造混沌序列。 Logistics 方程为
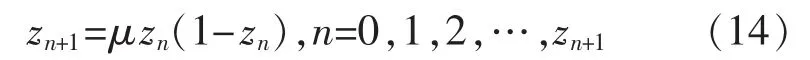
式中:μ 为控制参数。 当初值z0的取值在0~1 之间时,该系统完全处于混沌状态中,那么由此可迭代出时间序列z1,z2……。 在本文中选取μ 的值为4,具体混沌粒子群优化算法(CPOS)的搜索过程如图2所示。

图2 混沌粒子群优化算法(CPOS)的搜索过程Fig.2 Search process of chaotic particle swarm optimization algorithm(CPOS)
4 测试与分析
为了验证改进算法的有效性及准确性。 在本实验中,选用焦距为6 mm 的定焦工业镜头,标定板为棋盘格,X 方向的数目为7,Y 方向的数目为9,方格尺寸为30 mm×30 mm, 拍摄了12 幅不同方向的图像。
首先通过Matlab 标定工具箱求出相机内参的初始值,设置粒子数目为M=100,搜索空间的维数D=28。 根据坐标的对应关系,构造左右摄像机二维重投影平均误差函数作为优化目标函数, 如式(15):
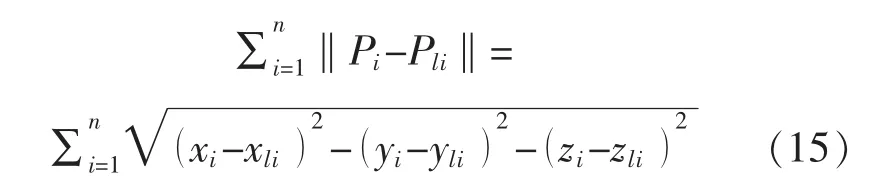
式中:Pi(xi,yi,zi)是空间点的三维坐标;n 代表标定点的个数。
实验中,在同一个标定的数据下,分别进行标定,并得出相机的重投影误差图。 如图3 表示使用张正友LM 算法重投影的误差结果; 图4 表示基于混沌粒子群算法得到的重投影的误差结果。 表1 是基于两种方法的误差对比,可以看出混沌粒子群算法优化了相机参数,使得重投影误差更小。 表2 为两种实验方法得到的内参数值的结果。 通过与张正友标定结果相比,该方法具有可行性并且结果更为精确。
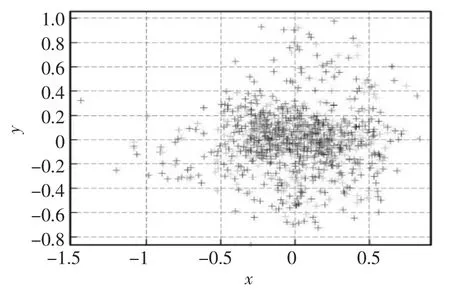
图3 张正友标定法投影误差图Fig.3 Projection error diagram of Zhang Zhengyou calibration method
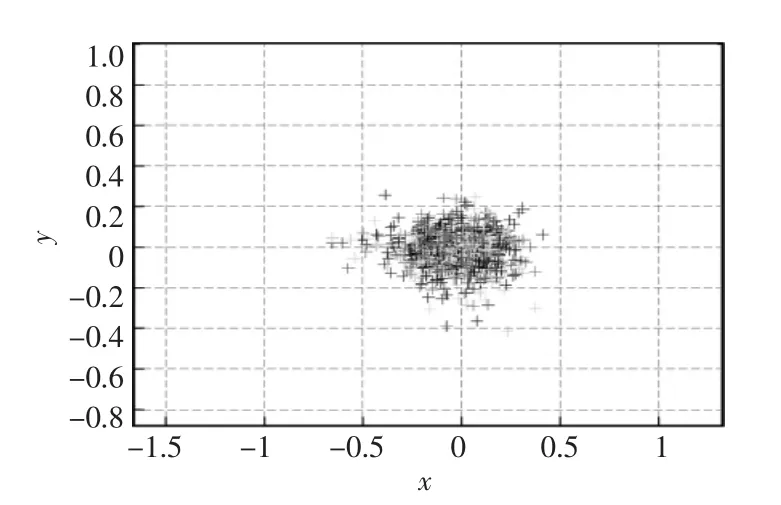
图4 基于混沌粒子群算法的投影误差图Fig.4 Projection error diagram based on chaoticparticle swarm optimization algorithm
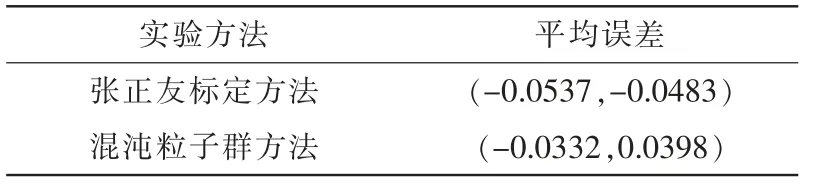
表1 平均误差对比Tab.1 Comparison of average errors
5 结语
相机的标定是获得目标点三维坐标值的关键步骤,本文在充分考虑了相机成像模型和张正友优化方法局限性的基础上,并且考虑到混沌粒子群算法在求解局部最优值的优势,提出一种基于混沌粒子群优化算法的相机参数标定方法。 先利用张正友标定法对摄像头进行标定,分析了张正友标定法在求解过程中存在的不足,提出基于混沌粒子群算法对相机参数进行优化, 通过最终的标定实验证明,基于混沌粒子群算法提高了标定的精度,得到了更为精确的实际三维坐标点和图像坐标点之间的对应关系。
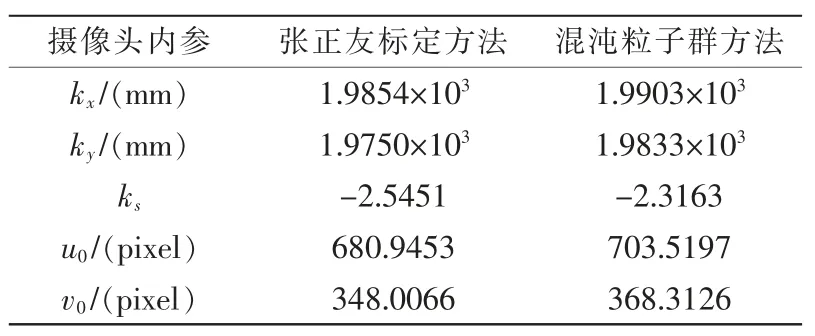
表2 两种实验方法得到的内参数值Tab.2 Internal parameter values obtained by two experimental methods
