水下遥控机器人运动仿真数学模型的研究
2019-05-09张美荣
张美荣
(海洋石油工程股份有限公司,天津300451)
水下遥控机器人ROV 模拟器必须能够正确地描述ROV 的运动, 建立能够反映ROV 运动的特征、变化规律及本船与其他实体相互作用关系的船舶运动数学模型,对ROV 各类作业的动力学、运动学模型构建及解算。 这些是模拟器研制成功的关键。 模拟器位置变化、各种运动参数等均依赖于数学模型的解算,是衡量模拟器逼真度的核心指标。
近年来, 一些学者针对建立适用于ROV 的运动数学模型进行了研究。 文献[1]通过变漂角和变攻角的模型试验,测得全漂角和全攻角变化范围内的水动力;文献[2]采用带有截距项的平方项模型,进行大漂角、 大功角运动状态下水动力的模拟仿真;文献[3]通过试验得到潜水器随攻角变化的受力/力矩曲线。 在此,研究水下遥控机器人运动仿真数学模型,实时解算ROV 在海洋环境条件(浪、流)作用下,依靠自身推进器产生的推力而自主航行时的运动速度、位置和姿态;仿真精度要求,与实船监测数据对比, 自航和动力定位模式下的误差均小于15%,满足视景仿真对于实时性的要求[4]。
1 ROV 运动数学模型系统分解
为实现ROV 运动数学模型的主要功能, 根据模块化思想,将其分为ROV 运动模块和ROV 推力模块。 该系统的任务分解如图1 所示。
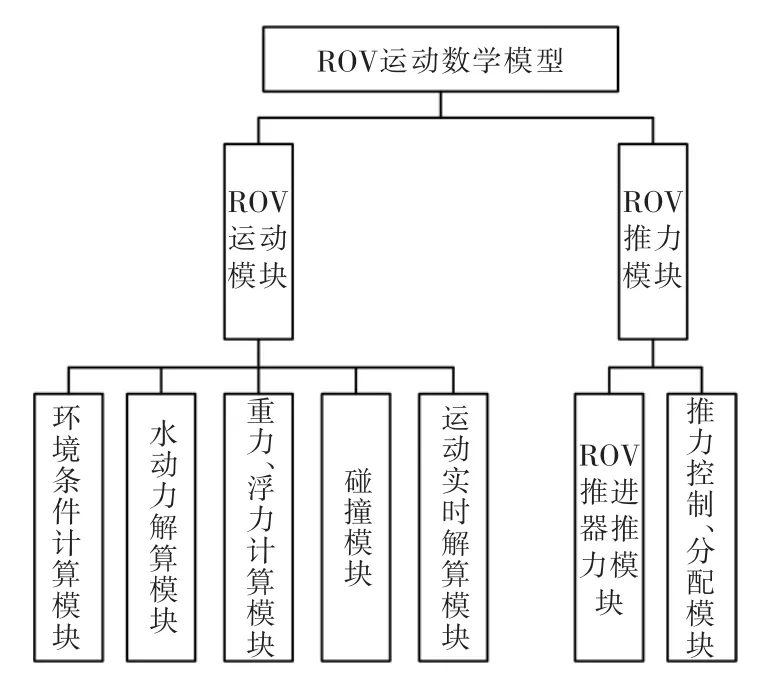
图1 ROV 运动数学模型系统的任务分解Fig.1 Task decomposition of ROV motion mathematical model system
1)ROV 运动模块
ROV 运动模块用于实时解算在给定推力作用下,ROV 在环境条件(浪、流)作用下的六自由度耦合运动速度、位置和姿态。 具体包括:
①环境条件计算模块 建立海洋环境(浪、流)的数学模型,考虑海洋环境(浪、流)对于ROV 运动的影响。 先通过海洋环境数学模型得到在惯性坐标系下海浪、海流的速度,然后将其转化到ROV 运动坐标系下,最后得到ROV 相对于海洋环境的运动速度。
②水动力解算模块 建立一种适用于ROV 运动特性的耦合水动力数学模型,并获得一套适用于ROV 的惯性、黏性水动力系数,计算ROV 运动过程中所遭受到的耦合黏性、惯性水动力。
③重力、 浮力计算模块 根据ROV 当前的重力、浮力以及姿态,解算ROV 运动过程中所受的恢复力、力矩。
④碰撞模块 对ROV 在水下作业操作中出现的碰撞、干涉情况进行判断,提供报警等信息,并根据ROV 当前的运动状态与当前环境情况, 实时解算出ROV 遭受撞击后的运动状态。
⑤运动实时解算模块 综合ROV 受到的作用力、 力矩, 运用数值计算方法实时解算ROV 运动学、动力学微分方程,获得ROV 实时运动速度、位置和姿态。
2)ROV 推力模块
ROV 推力模块用于实时计算ROV 推进器产生的推力、 力矩, 并传递给ROV 运动模块用以解算ROV 当前运动状态。 具体包括:
①ROV 推进器推力模块 依据推进器试验曲线,建立单个推进器的液压-推力模型,得到在不同压力输入下推进器的推力,再考虑各推进器的安装位置与角度, 得到各推进器作用下ROV 受到的总推力、力矩。
②推力控制、 分配模块 在ROV 自动驾驶状态下(定向、定深、定速和定位)使用。 先通过控制算法实时计算控制ROV 运动所需的总推力、力矩,再通过推力分配算法把推力分配到各推进器上[5]。
2 ROV 系统运动仿真数学模型
2.1 坐标系的选取与运动参数的定义
ROV 在水下采用六自由度空间运动的方式,在水下运动时主要受到重力、浮力、拖缆拉力、惯性类水动力及黏性类水动力的作用。 为便于研究,选取空间固定坐标系(Earth-fixed)O-XYZ 和随体坐标系(Body-fixed)G-X0Y0Z0,如图2 所示。 固定坐标系中,运动姿态由欧拉角φ,θ,ψ 表示;其中φ 为横倾角,θ 为俯仰角,ψ 为艏摇角;方向分别以沿OX,OY,OZ轴的正向顺时针方向绕为正。
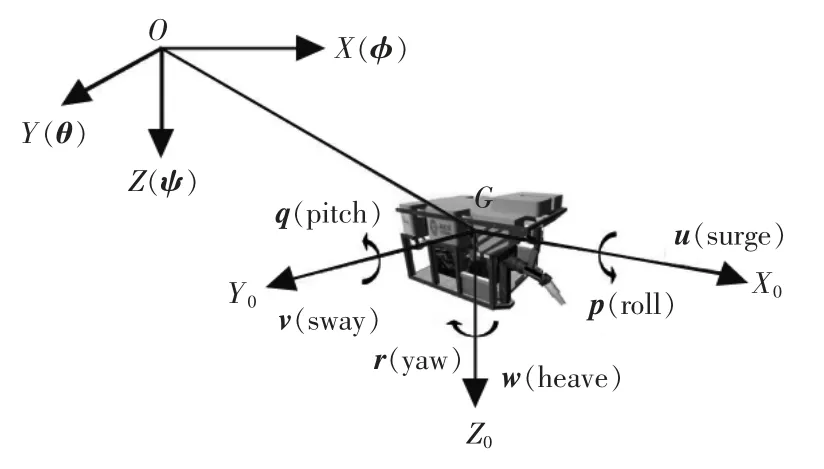
图2 固定坐标系与随体坐标系Fig.2 Fixed coordinate system and satellite coordinate system
ROV 的运动速度v 由随体坐标系G-X0Y0Z0中定义的物理量u(纵向速度)、v(横向速度)、w(垂向速度)描述,分别为对应坐标轴GX0,GY0,GZ0做纵向、横向、升沉运动时的线速度。
ROV 运动角速度Ω 由随体坐标系G-X0Y0Z0中定义的物理量p(横倾角速度)、q(俯仰角速度)、r(摇艏角速度)描述,方向分别为沿坐标轴GX0,GY0,GZ0正向顺时针方向绕为正。
ROV 的力矩M0由随体坐标系G-X0Y0Z0中定义的物理量K(横倾力矩)、M(俯仰力矩)、N(摇艏力矩)描述,分别为ROV 运动时所受力距对应于坐标轴GX0,GY0,GZ0的分量。 各参数见表1。

表1 运动和动力参数Tab.1 Motion and dynamic parameters
2.2 ROV 运动学方程
ROV 单体运动数学模型建模仅考虑单个ROV的运用,不考虑与缆线、机械手的耦合运动;模拟出单体ROV 在无限水深、大攻角、大漂角、近海底运动,并受海流作用下的速度和位置姿态。
考虑环境扰动(浪、流),ROV 六自由度动力学、运动学方程为

式中:vr为ROV 相对于环境的运动速度;vc为海流速度;M 为惯性矩阵,包括ROV 质量矩阵MRB和附加质量矩阵MA;C 为科氏力矩阵;D 为ROV 受到的阻尼力作用;g 为恢复力, 包含推进器施加于ROV上的推力。
2.3 ROV 推进器建模
ROV 推进器的建模是根据ROV 推进器液压-推力曲线,获得推进器推力与压力之间的函数表达式, 再根据各推进器的位置得到作用在ROV 上的总推力。 ROV 各推进器位置以及各推进器对ROV的作用力如图3 所示。
3 验证试验
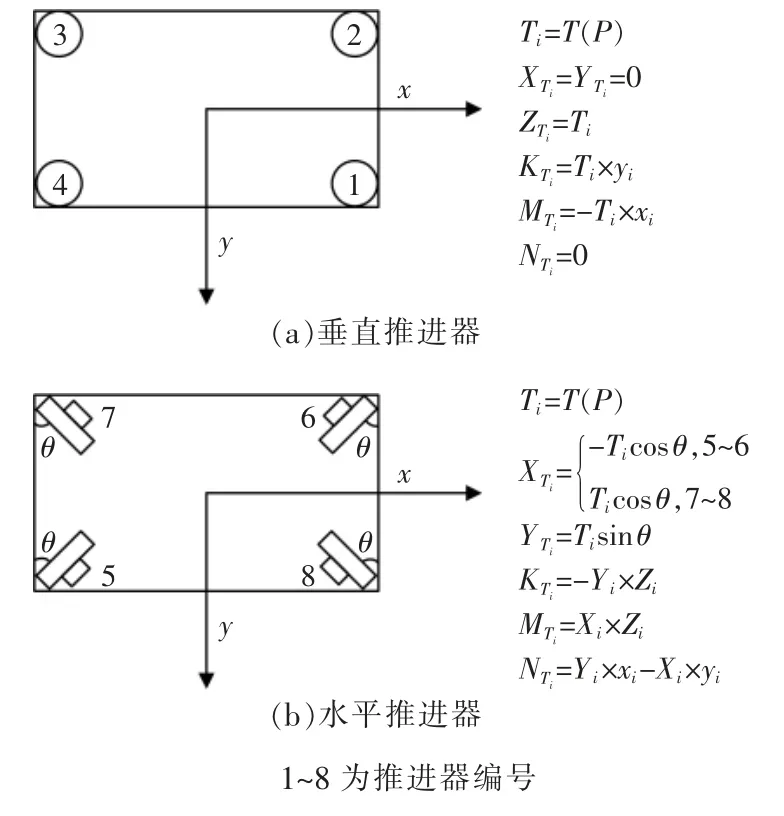
图3 推进器布置与作用力Fig.3 Propeller arrangement and acting force
ROV 本体实物如图4a 所示。 因无法获取ROV实船的试验数据,故采用缩比模型试验与仿真数学模型相对比的方法进行模型准确度测试。 缩小比例为1∶4 的ROV 试验模型如图4b 所示, 试验的基础参数见表2。

图4 ROV 本体和试验用模型Fig.4 ROV ontology picture and experimental model
4 仿真数据与试验数据对比分析
4.1 纵向直航测试
模型的X0,Y0,Z0轴分别平行于来 流方向,模型固定于水槽内, 测定不同流速作用下模型所受阻力,以获取各方向的阻力系数。
设定纵向速度不为零,其他方向的速度均为0;试验流速为0.3~0.8 m/s,加速度全部为0;侧向力Y,横倾力矩K 及摇艏力矩N 忽略不计。纵向直航测试的试验数据见表3。
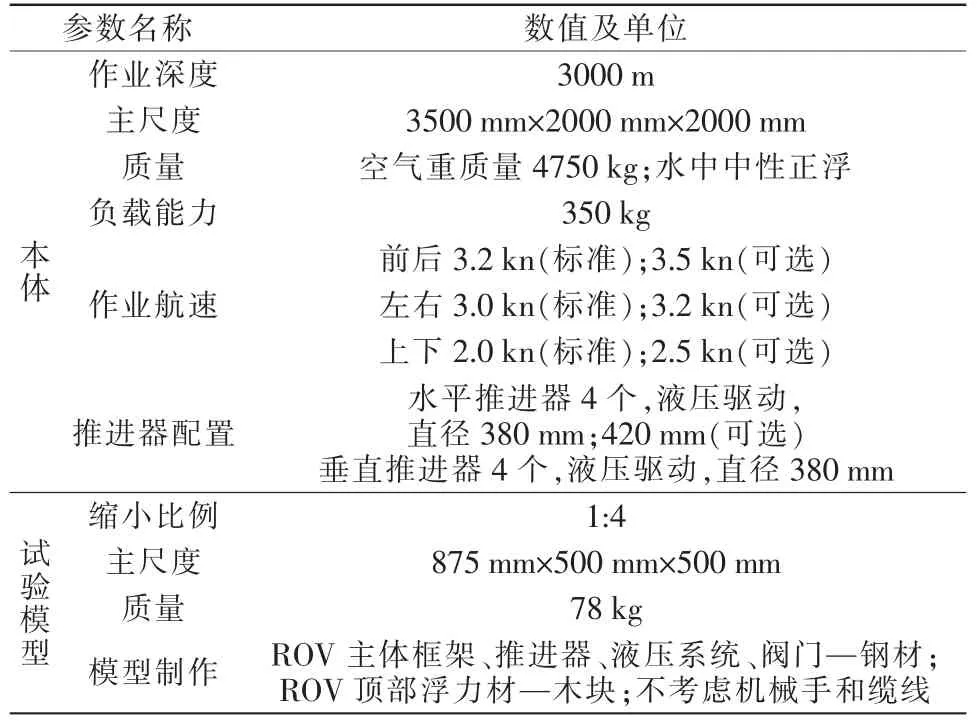
表2 ROV 本体及其试验模型的参数Tab.2 Parameters of ROV ontology and its test model
由表可知, 纵向直航仿真前进方向, 纵向力X的最大误差为9.1%,垂向力Z 的最大误差为9.6%,俯仰力矩M 的最大误差为7.8%; 纵向直航仿真后退方向,纵向力X 的最大误差为7.7%,垂向力Z 的最大误差为7.9%,俯仰力矩M 的最大误差为8.2%。
4.2 垂向直航测试
设定垂向速度不为零,其他方向的速度均为0;试验流速为0.2~0.6 m/s,加速度全部为0;侧向力Y,横倾力矩K 及摇艏力矩N 忽略不计。垂向直航测试的试验数据见表3。
由表可知, 垂向直航仿真下降方向, 纵向力X的最大误差为8.1%,垂向力Z 的最大误差为8.3%,俯仰力矩M 的最大误差为8.7%; 垂向直航仿真上升方向,纵向力X 的最大误差为6.8%,垂向力Z 的最大误差为9.4%,俯仰力矩M 的最大误差为8.3%。
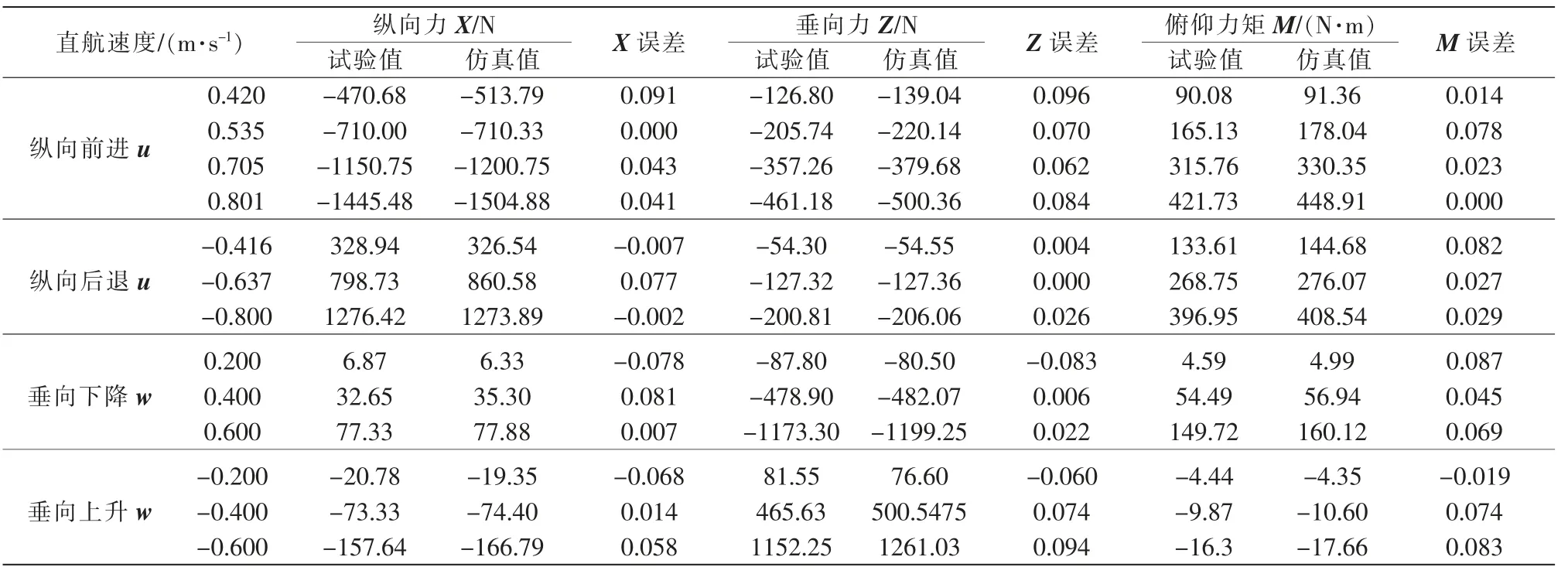
表3 纵向和垂向直航测试的试验数据Tab.3 Test data of longitudinal and vertical direct flight tests
4.3 侧向直航测试
设定侧向速度不为零,其他方向的速度均为0;速度测定范围为0.2~0.6 m/s,加速度全部为0;纵向力X 和横倾力矩K 忽略不计。侧向直航测试数据见表4。
由表可见,侧向直航仿真的侧向力Y 误差最大为8.7%,垂向力Z 的最大误差为8.8%,俯仰力矩M的最大误差为5.7%,摇艏力矩N 的最大误差为9.6%。
4.4 俯仰试验
在一定流速下,试验模型以一定振幅、频率做摇荡试验,通过测试侧向力和摇艏力矩来验证模型的准确性。

表4 侧向直航测试Tab.4 Lateral direct flight test
设定俯仰试验1 的纵向速度为0.529 m/s,其他方向的速度为0,只有侧向力Y 和艏摇力矩N 随加速度变化而改变,试验结果见表5。
另设定俯仰试验2 的纵向速度为0.748 m/s,其他方向的速度为0,试验结果见表5。
由表可知,俯仰试验侧向力Y 的最大误差为9.5%,摇艏力矩N 的最大误差为8.2%。
通过以上对比分析可知,运动仿真模型的试验数据误差均小于10%,模型可用。
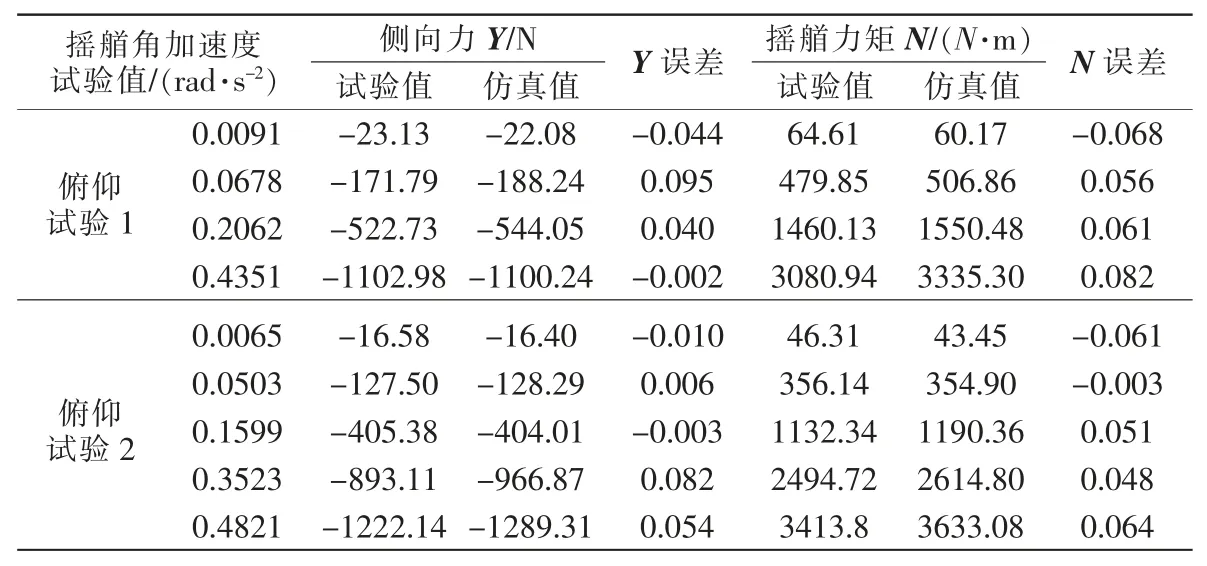
表5 俯仰试验结果Tab.5 Pitch experiment
5 结语
ROV 运动数学模型的仿真结果表明,该运动模型能够真实准确地反映ROV 运动的特征。 该运动数学模型考虑了环境条件对于运动结果的影响。 经过试验证明,该运动方程实时性良好,能够良好地满足深水ROV 作业模拟器对于运动数学模型真实性与实时性的要求。
